六 回顾与整理(二)立体图形整理和复习(课件)人教版数学六年级下册
文档属性
| 名称 | 六 回顾与整理(二)立体图形整理和复习(课件)人教版数学六年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 13:44:02 | ||
图片预览



文档简介
(共20张PPT)
立体图形的整理和复习
——湖口县武山学校 沈洒
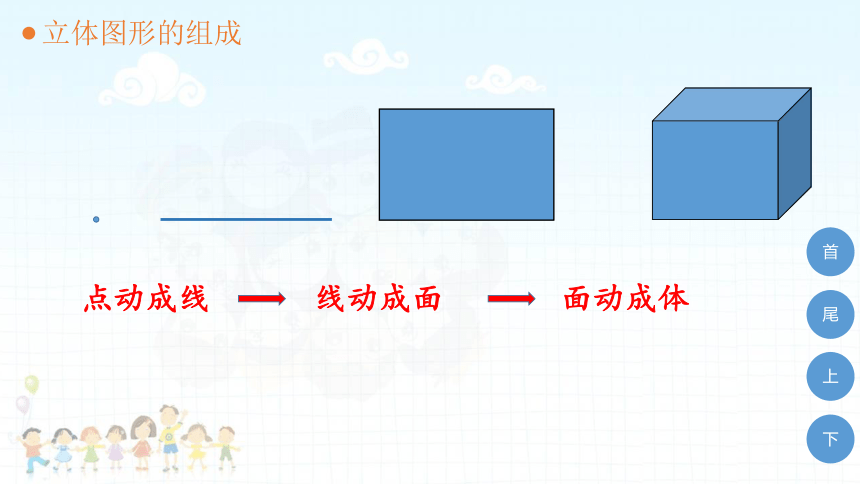
立体图形的组成
点动成线
线动成面
面动成体
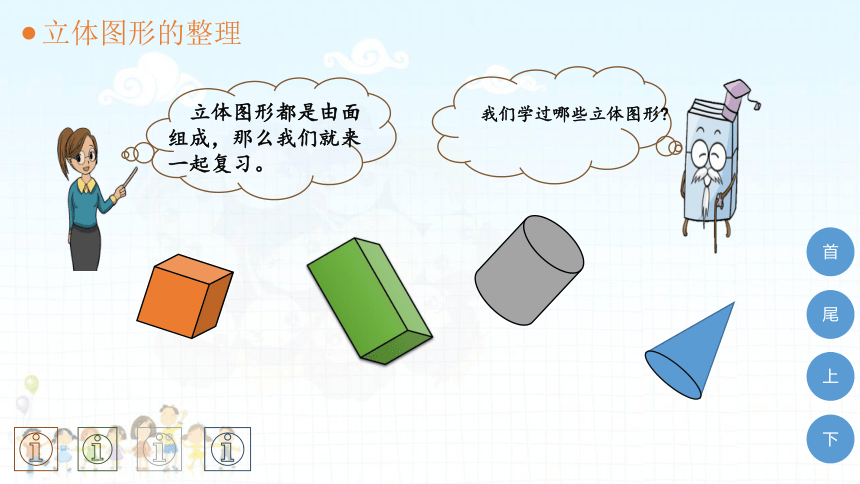
立体图形都是由面组成,那么我们就来一起复习。
我们学过哪些立体图形
立体图形的整理
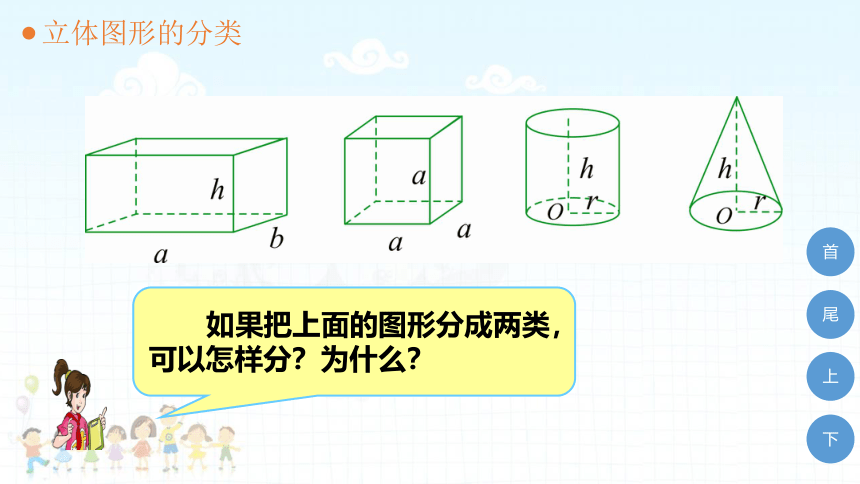
立体图形的分类
如果把上面的图形分成两类,
可以怎样分?为什么?
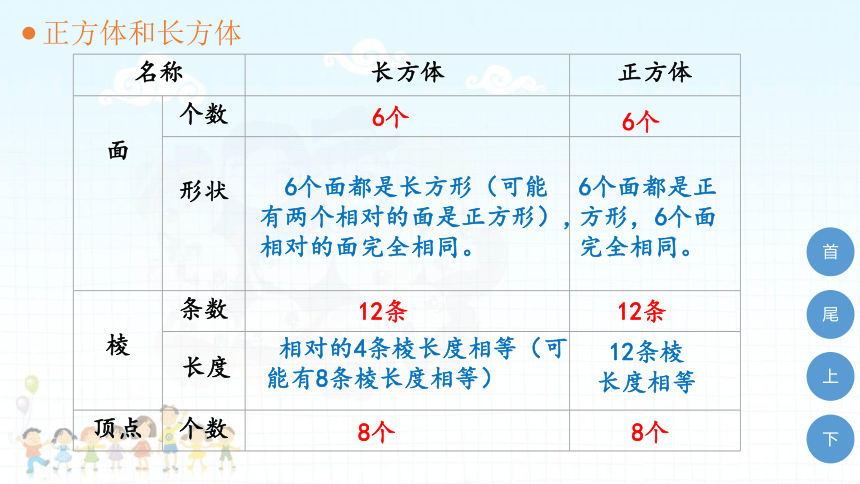
正方体和长方体
名称 长方体 正方体
面 个数
形状
棱 条数
顶点 个数
6个
6个面都是长方形(可能有两个相对的面是正方形),相对的面完全相同。
12条
相对的4条棱长度相等(可能有8条棱长度相等)
6个
6个面都是正方形,6个面完全相同。
12条
12条棱
长度相等
8个
长度
8个
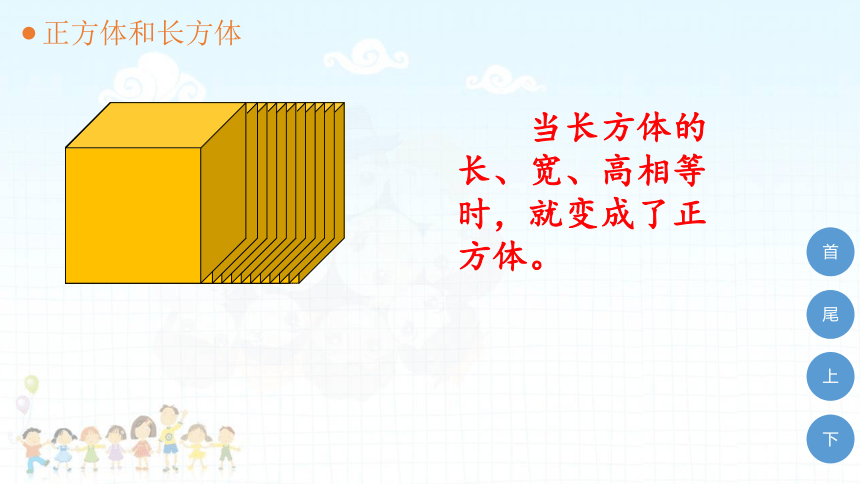
正方体和长方体
当长方体的长、宽、高相等时,就变成了正方体。
圆柱和圆锥
底面
侧面
高
只有一个
两个完全一样的圆
只有一条
有无数条
曲面,展开后是扇形
曲面,沿高展开后是长方形(正方形)
表面积
什么叫做立体图形的表面积?
一个立体图形的所有面的总和
长方体表面积
正方体表面积
圆柱表面积
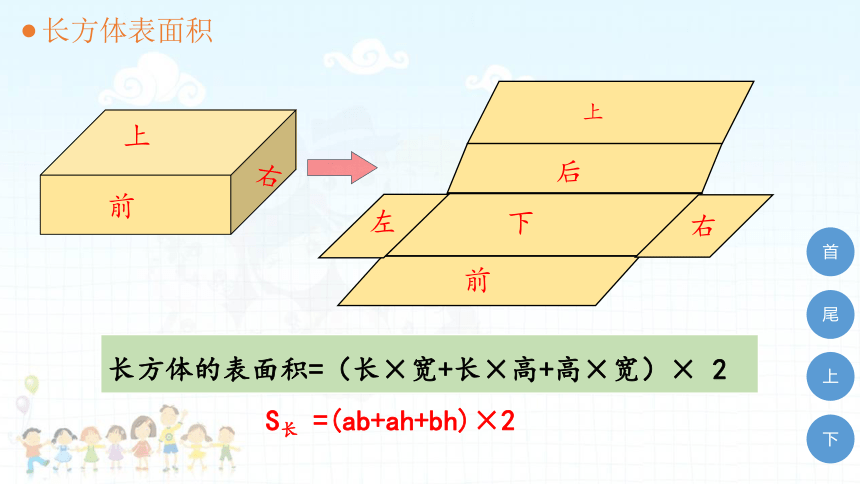
长方体表面积
上
前
右
长方体的表面积=(长×宽+长×高+高×宽)× 2
S长 =(ab+ah+bh)×2
上
下
前
后
左
右
正方体表面积
正方体的表面积=棱长×棱长×6
S正=6a2
上
下
后
左
右
圆柱表面积
底面
底面
圆柱的表面积=侧面积+两个底面的面积
侧 面
S表=2S底+S侧 S侧=Ch
体积
将一块石头放进装有水的圆柱形容器里,会有什么现象?
水面上升
石头占了一部分水的空间
立体图形所占空间的大小就是它的体积
长方体体积
a厘米
b厘米
h
厘
米
长方体的体积 = 长×宽×高
V =ɑbh
正方体的体积 = 棱长×棱长×棱长
V =ɑ3
底面积×高
圆柱体积
底面积
V = Sh
高
高
底面积
高
圆柱的体积
=
×
长方体的体积 = 底面积
×
高
下面哪些立体图形的体积可以用“底面积×高”计算
圆锥体积
圆锥的体积等于与它等底等高圆柱体积的三分之一。
圆锥的体积= × 底面积×高
Ⅴ = Ⅴ =
圆锥
圆柱
sh
表面积和体积计算公式
立体 图形 表面积 体积
S长=(ab+ah+bh)×2
S正=6a2
S表=2S底+S侧
S侧=Ch
V长=abh
V正=a3
V柱=Sh
V=Sh
Ⅴ =
锥
sh
1
3
—
公园里有一座如图所示的房子,这座房子的体积是多少立方米?
巩固练习
巩固练习
有两种生日蛋糕:
(1)如果在蛋糕外面涂一层奶油,哪个
涂的比较多?
12
厘
米
20厘米
20厘米
15厘米
12厘米
(2)如果两者的价格一样,你会选哪个?
将一个圆柱体沿着底面直径切成两个半圆柱,表面积增加了40平方厘米,圆柱的底面直径为4厘米,这个圆柱的体积是多少立方厘米
巩固练习
立体图形的整理和复习
——湖口县武山学校 沈洒
立体图形的组成
点动成线
线动成面
面动成体
立体图形都是由面组成,那么我们就来一起复习。
我们学过哪些立体图形
立体图形的整理
立体图形的分类
如果把上面的图形分成两类,
可以怎样分?为什么?
正方体和长方体
名称 长方体 正方体
面 个数
形状
棱 条数
顶点 个数
6个
6个面都是长方形(可能有两个相对的面是正方形),相对的面完全相同。
12条
相对的4条棱长度相等(可能有8条棱长度相等)
6个
6个面都是正方形,6个面完全相同。
12条
12条棱
长度相等
8个
长度
8个
正方体和长方体
当长方体的长、宽、高相等时,就变成了正方体。
圆柱和圆锥
底面
侧面
高
只有一个
两个完全一样的圆
只有一条
有无数条
曲面,展开后是扇形
曲面,沿高展开后是长方形(正方形)
表面积
什么叫做立体图形的表面积?
一个立体图形的所有面的总和
长方体表面积
正方体表面积
圆柱表面积
长方体表面积
上
前
右
长方体的表面积=(长×宽+长×高+高×宽)× 2
S长 =(ab+ah+bh)×2
上
下
前
后
左
右
正方体表面积
正方体的表面积=棱长×棱长×6
S正=6a2
上
下
后
左
右
圆柱表面积
底面
底面
圆柱的表面积=侧面积+两个底面的面积
侧 面
S表=2S底+S侧 S侧=Ch
体积
将一块石头放进装有水的圆柱形容器里,会有什么现象?
水面上升
石头占了一部分水的空间
立体图形所占空间的大小就是它的体积
长方体体积
a厘米
b厘米
h
厘
米
长方体的体积 = 长×宽×高
V =ɑbh
正方体的体积 = 棱长×棱长×棱长
V =ɑ3
底面积×高
圆柱体积
底面积
V = Sh
高
高
底面积
高
圆柱的体积
=
×
长方体的体积 = 底面积
×
高
下面哪些立体图形的体积可以用“底面积×高”计算
圆锥体积
圆锥的体积等于与它等底等高圆柱体积的三分之一。
圆锥的体积= × 底面积×高
Ⅴ = Ⅴ =
圆锥
圆柱
sh
表面积和体积计算公式
立体 图形 表面积 体积
S长=(ab+ah+bh)×2
S正=6a2
S表=2S底+S侧
S侧=Ch
V长=abh
V正=a3
V柱=Sh
V=Sh
Ⅴ =
锥
sh
1
3
—
公园里有一座如图所示的房子,这座房子的体积是多少立方米?
巩固练习
巩固练习
有两种生日蛋糕:
(1)如果在蛋糕外面涂一层奶油,哪个
涂的比较多?
12
厘
米
20厘米
20厘米
15厘米
12厘米
(2)如果两者的价格一样,你会选哪个?
将一个圆柱体沿着底面直径切成两个半圆柱,表面积增加了40平方厘米,圆柱的底面直径为4厘米,这个圆柱的体积是多少立方厘米
巩固练习
