人教A版(2019)高中数学必修第一册 2.2基本不等式 课件(共19张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第一册 2.2基本不等式 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 642.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 14:24:04 | ||
图片预览






文档简介
(共19张PPT)
2.2 基本不等式
第二章 一元二次函数、方程和不等式
目录
二、知识讲解
三、小结
四、练习
一、上节回溯
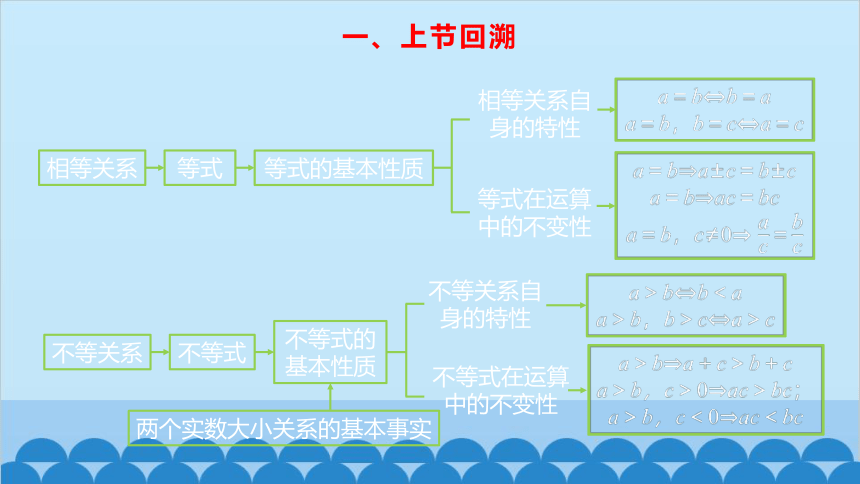
一、上节回溯
相等关系
等式
等式的基本性质
相等关系自身的特性
等式在运算中的不变性
不等关系
不等式
不等式的基本性质
不等关系自身的特性
不等式在运算中的不变性
两个实数大小关系的基本事实
二、知识讲解
1.基本不等式
二、知识讲解
1.基本不等式
二、知识讲解
1.基本不等式
二、知识讲解
在图中,AB 是圆的直径,点 C 是 AB 上一点,AC=a,
BC=b.过点 C 作垂直于 AB 的弦 DE,连接 AD,BD.你
能利用这个图形,得出基本不等式的几何解释吗?
探究
A
B
C
D
E
a
b
1.基本不等式
二、知识讲解
1.基本不等式
二、知识讲解
1.基本不等式
二、知识讲解
1.基本不等式
基本不等式在解决实际问题中有广泛的应用,是解决最大(小)值问题的有力工具.
二、知识讲解
例3 (1)用篱笆围一个面积为 100 m2 的矩形菜园,当这个矩形的边长为多少时,所用篱笆最短?最短篱笆的长度是多少?
分析:(1) 矩形菜园的面积是矩形的两邻边之积,于是问题转化为:矩形的邻边之积为定值,边长多大时周长最短.
2.基本不等式的应用
二、知识讲解
例3 (2)用一段长为 36 m 的篱笆围成一个矩形菜园,当这个矩形的边长为多少时,菜园的面积最大?最大面积是多少?
分析:(2)矩形菜园的周长是矩形两邻边之和的 2 倍,于是问题转化为:矩形的邻边之和为定值,边长多大时面积最大.
2.基本不等式的应用
二、知识讲解
例4 某工厂要建造一个长方体形无盖贮水池,其容积为 4 800 m3,深为 3 m.如果池底每平方米的造价为 150 元,池壁每平方米的造价为 120 元,那么怎样设计水池能使总造价最低?最低总造价是多少?
分析:贮水池呈长方体形,它的高是 3 m,池底的边长没有确定.如果池底的边长确定了,那么水池的总造价也就确定了.因此,应当考察池底的边长取什么值时,水池的总造价最低.
2.基本不等式的应用
三、小结
应用
定义
基本不等式
几何解释
证明方法
四、练习
四、练习
四、练习
四、练习
谢谢观看
2.2 基本不等式
第二章 一元二次函数、方程和不等式
目录
二、知识讲解
三、小结
四、练习
一、上节回溯
一、上节回溯
相等关系
等式
等式的基本性质
相等关系自身的特性
等式在运算中的不变性
不等关系
不等式
不等式的基本性质
不等关系自身的特性
不等式在运算中的不变性
两个实数大小关系的基本事实
二、知识讲解
1.基本不等式
二、知识讲解
1.基本不等式
二、知识讲解
1.基本不等式
二、知识讲解
在图中,AB 是圆的直径,点 C 是 AB 上一点,AC=a,
BC=b.过点 C 作垂直于 AB 的弦 DE,连接 AD,BD.你
能利用这个图形,得出基本不等式的几何解释吗?
探究
A
B
C
D
E
a
b
1.基本不等式
二、知识讲解
1.基本不等式
二、知识讲解
1.基本不等式
二、知识讲解
1.基本不等式
基本不等式在解决实际问题中有广泛的应用,是解决最大(小)值问题的有力工具.
二、知识讲解
例3 (1)用篱笆围一个面积为 100 m2 的矩形菜园,当这个矩形的边长为多少时,所用篱笆最短?最短篱笆的长度是多少?
分析:(1) 矩形菜园的面积是矩形的两邻边之积,于是问题转化为:矩形的邻边之积为定值,边长多大时周长最短.
2.基本不等式的应用
二、知识讲解
例3 (2)用一段长为 36 m 的篱笆围成一个矩形菜园,当这个矩形的边长为多少时,菜园的面积最大?最大面积是多少?
分析:(2)矩形菜园的周长是矩形两邻边之和的 2 倍,于是问题转化为:矩形的邻边之和为定值,边长多大时面积最大.
2.基本不等式的应用
二、知识讲解
例4 某工厂要建造一个长方体形无盖贮水池,其容积为 4 800 m3,深为 3 m.如果池底每平方米的造价为 150 元,池壁每平方米的造价为 120 元,那么怎样设计水池能使总造价最低?最低总造价是多少?
分析:贮水池呈长方体形,它的高是 3 m,池底的边长没有确定.如果池底的边长确定了,那么水池的总造价也就确定了.因此,应当考察池底的边长取什么值时,水池的总造价最低.
2.基本不等式的应用
三、小结
应用
定义
基本不等式
几何解释
证明方法
四、练习
四、练习
四、练习
四、练习
谢谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
