2022—2023学年人教版数学八年级上册 11.2.2三角形的外角 导学案 (含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册 11.2.2三角形的外角 导学案 (含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 247.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 11:51:02 | ||
图片预览


文档简介
11.2.2三角形的外角
【学习目标】
1.知道什么叫三角形的外角;理解三角形外角的两条性质定理;
2.能用三角形外角的有关定理解答问题。
【学习过程】
复习回顾:
1.三角形内角和定理:三角形的内角和等于 。
2.△ABC中 ∠A+∠B+∠C=
3.如图,在△ABC中∠A=60°,∠B=35°,则∠ACB= °,
∠ACD= °;
新课导入:
(一)认识三角形的外角,阅读课本,了解什么是三角形的外角,并回答下列问题:
1.如图,△ABC的一个外角是 ;
2.如图,∠C=50°,∠B=28°,则∠BAC= °∠DAB= °
(二)三角形外角的性质定理:
1.如图,△ABC的一个外角是 ,
和它不相邻的内角是 , 。
2.猜想:∠BAD和∠B、∠C之间的关系是 。
证明:
归纳:①三角形的一个外角等于 ;
②三角形的一个外角大于一个 。
几何语言: ∠1=∠ +∠ ;
∠ABE= + ;
∠1 >∠ ; ∠1 >∠ ;
(三)三角形的外角和:每一个三角形的内角相应地取其中一个外角相加的结果;
思考:如图,∠1+∠2+∠3= °(你能证明得到的结论吗?)
归纳:三角形的外角和等于 °
三、巩固练习:
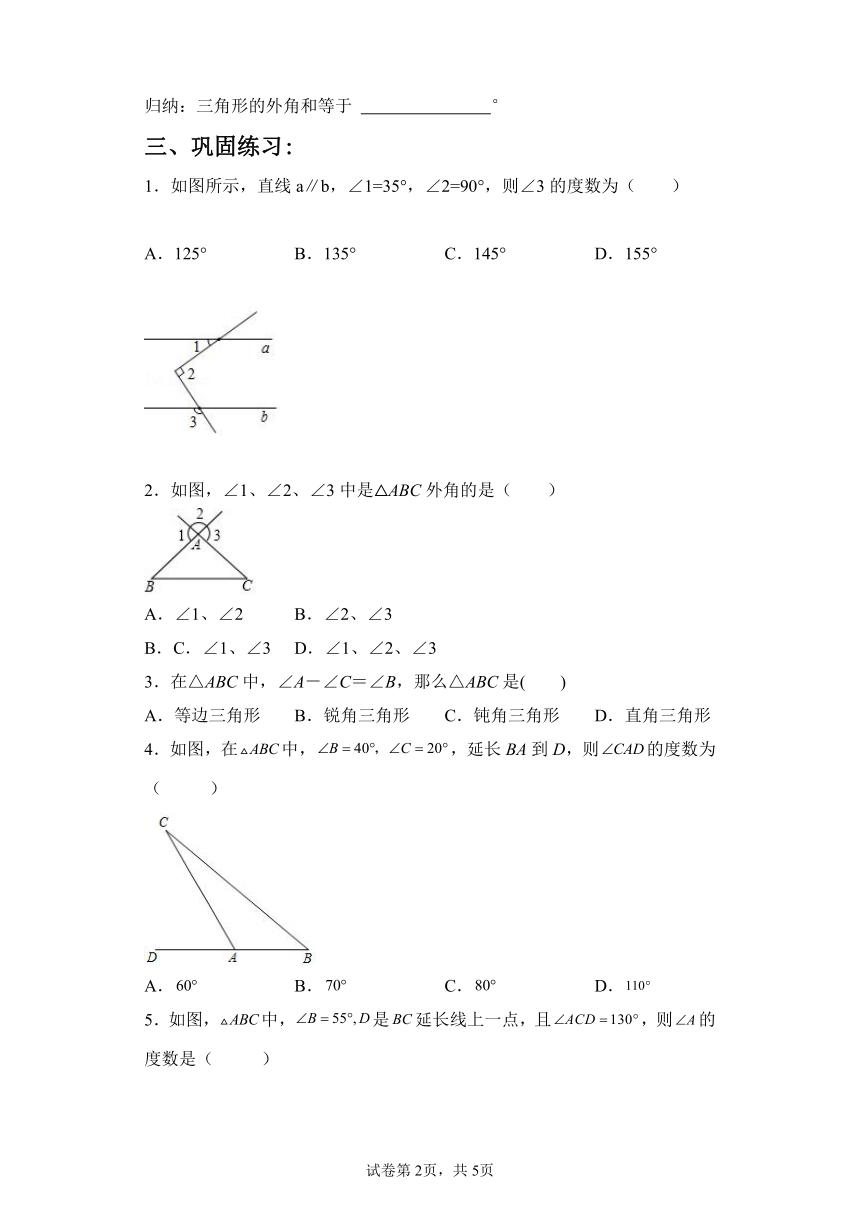
1.如图所示,直线a∥b,∠1=35°,∠2=90°,则∠3的度数为( )
A.125° B.135° C.145° D.155°
2.如图,∠1、∠2、∠3中是△ABC外角的是( )
∠1、∠2 B.∠2、∠3
C.∠1、∠3 D.∠1、∠2、∠3
3.在△ABC中,∠A-∠C=∠B,那么△ABC是( )
A.等边三角形 B.锐角三角形 C.钝角三角形 D.直角三角形
4.如图,在中,,延长BA到D,则的度数为( )
A. B. C. D.
5.如图,中,是延长线上一点,且,则的度数是( )
A. B. C. D.
6.如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.
7.如图,,点为上一点,、的角平分线交于点,已知,则________度.
8.如图,E为△ABC的BC边上一点,点D在BA的延长线上,DE交AC于点F,∠B=46°,∠C=30°,∠EFC=70°,则∠D=______.
9.(1)如图(a),BD平分,CD平分.试确定和的数量关系.
(2)如图(b),BE平分,CE平分外角.试确定和的数量关系.
(3)如图(c),BF平分外角,CF平分外角.试确定和的数量关系.
10.如图,∠CBF,∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC,∠CBF的平分线BD,BE交于点D,E.
(1)若∠A=70°,求∠D的度数;
(2)若∠A=a,求∠E;
(3)连接AD,若∠ACB=,则∠ADB= .
11.在△ABC中,BD平分∠ABC交AC于点D,点E是射线AC上的动点(不与点D重合),过点E作EF∥BC交直线BD于点F,∠CEF的角平分线所在直线与射线BD交于点G.
(1)如图1,点E在线段AD上运动.
①若∠ABC=40°,∠C=60°,则∠BGE=______°;
②若∠A=70°,则∠BGE=______;
③探究∠BGE与∠A之间的数量关系
(2)若点E在射线DC上运动时,∠BGE与∠A之间的数量关系与(1)③中的数量关系是否相同?若不同,请写出它们之间的数量关系.
参考答案:
1.A
2.C
3.D
4.A
5.C
6.15°##15度
7.
8.34°##34度
9.(1);(2);(3)
10.(1)35°;(2)90°-α;(3)β
11.(1)①50°;②55°;③∠BGE=90°-∠A,;
(2)不同,当点E在线段CD上,∠BGE=∠A;当点E在DC的延长线上,∠BGE=90°+∠A,
试卷第1页,共3页
试卷第1页,共3页
【学习目标】
1.知道什么叫三角形的外角;理解三角形外角的两条性质定理;
2.能用三角形外角的有关定理解答问题。
【学习过程】
复习回顾:
1.三角形内角和定理:三角形的内角和等于 。
2.△ABC中 ∠A+∠B+∠C=
3.如图,在△ABC中∠A=60°,∠B=35°,则∠ACB= °,
∠ACD= °;
新课导入:
(一)认识三角形的外角,阅读课本,了解什么是三角形的外角,并回答下列问题:
1.如图,△ABC的一个外角是 ;
2.如图,∠C=50°,∠B=28°,则∠BAC= °∠DAB= °
(二)三角形外角的性质定理:
1.如图,△ABC的一个外角是 ,
和它不相邻的内角是 , 。
2.猜想:∠BAD和∠B、∠C之间的关系是 。
证明:
归纳:①三角形的一个外角等于 ;
②三角形的一个外角大于一个 。
几何语言: ∠1=∠ +∠ ;
∠ABE= + ;
∠1 >∠ ; ∠1 >∠ ;
(三)三角形的外角和:每一个三角形的内角相应地取其中一个外角相加的结果;
思考:如图,∠1+∠2+∠3= °(你能证明得到的结论吗?)
归纳:三角形的外角和等于 °
三、巩固练习:
1.如图所示,直线a∥b,∠1=35°,∠2=90°,则∠3的度数为( )
A.125° B.135° C.145° D.155°
2.如图,∠1、∠2、∠3中是△ABC外角的是( )
∠1、∠2 B.∠2、∠3
C.∠1、∠3 D.∠1、∠2、∠3
3.在△ABC中,∠A-∠C=∠B,那么△ABC是( )
A.等边三角形 B.锐角三角形 C.钝角三角形 D.直角三角形
4.如图,在中,,延长BA到D,则的度数为( )
A. B. C. D.
5.如图,中,是延长线上一点,且,则的度数是( )
A. B. C. D.
6.如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.
7.如图,,点为上一点,、的角平分线交于点,已知,则________度.
8.如图,E为△ABC的BC边上一点,点D在BA的延长线上,DE交AC于点F,∠B=46°,∠C=30°,∠EFC=70°,则∠D=______.
9.(1)如图(a),BD平分,CD平分.试确定和的数量关系.
(2)如图(b),BE平分,CE平分外角.试确定和的数量关系.
(3)如图(c),BF平分外角,CF平分外角.试确定和的数量关系.
10.如图,∠CBF,∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC,∠CBF的平分线BD,BE交于点D,E.
(1)若∠A=70°,求∠D的度数;
(2)若∠A=a,求∠E;
(3)连接AD,若∠ACB=,则∠ADB= .
11.在△ABC中,BD平分∠ABC交AC于点D,点E是射线AC上的动点(不与点D重合),过点E作EF∥BC交直线BD于点F,∠CEF的角平分线所在直线与射线BD交于点G.
(1)如图1,点E在线段AD上运动.
①若∠ABC=40°,∠C=60°,则∠BGE=______°;
②若∠A=70°,则∠BGE=______;
③探究∠BGE与∠A之间的数量关系
(2)若点E在射线DC上运动时,∠BGE与∠A之间的数量关系与(1)③中的数量关系是否相同?若不同,请写出它们之间的数量关系.
参考答案:
1.A
2.C
3.D
4.A
5.C
6.15°##15度
7.
8.34°##34度
9.(1);(2);(3)
10.(1)35°;(2)90°-α;(3)β
11.(1)①50°;②55°;③∠BGE=90°-∠A,;
(2)不同,当点E在线段CD上,∠BGE=∠A;当点E在DC的延长线上,∠BGE=90°+∠A,
试卷第1页,共3页
试卷第1页,共3页
