2022—2023学年人教版数学八年级上册 11.3.1 多边形 导学案 (含简单答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册 11.3.1 多边形 导学案 (含简单答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 137.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 00:00:00 | ||
图片预览

文档简介
11.3.1多边形
【学习目标】
1.知道多边形、多边形的内角、多边形的外角、多边形的对角线和正多边形的有关概念。
2.能够解决与多边形的对角线有关的问题。
【学习过程】
一、导入新课。
1.三角形概念: 。
2.除之前学习过的三角形外,你能找到哪些我们熟悉的图形?
二、主题探究。
(一)自主学习——类比三角形的有关概念探索多边形的有关概念
问题1:动手画一个多边形,类比三角形的概念,你能说出什么是多边形吗?
定义:在平面内,由一些线段首尾顺次相接组成的封闭图像叫做多边形。
问题2:根据图示,类比三角形的有关概念,说明什么是多边形的内角、外角和对角线
(1)多边形相邻两边组成的角叫做多边形的内角。
(2)多边形的边与它的邻边的延长线组成的角叫做多边形的外角。
(3)连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。
问题3:多边形的表示:用表示它的各个顶点的字母表示,要按定点的顺序书写,可以按顺时针或逆时针的顺序。
(二)合作探究——凸多边形和凹多边形
问题1:如图。观察这两个图形,找出相同点和不同点。
相同点:
不同点:
在图(1)中,画出四边形ABCD的任何一条边所在的直线,整个图形都在这条直线的同一侧,这样的四边形叫做凸四边形,这样的多边形称为凸多边形;
而图(2)就不满足上述凸多边形的特征,因为我们画CD(或BD)所在直线,整个多边形不都在这条直线的同一侧,我们称它为凹多边形。
注意:本节课我们只讨论凸多边形,今后习题、练习中提到的多边形也都是凸多边形。
问题2:判断一个多边形是凸多边形还是凹多边形的经验 。
(三)合作探究——正多边形的概念和性质
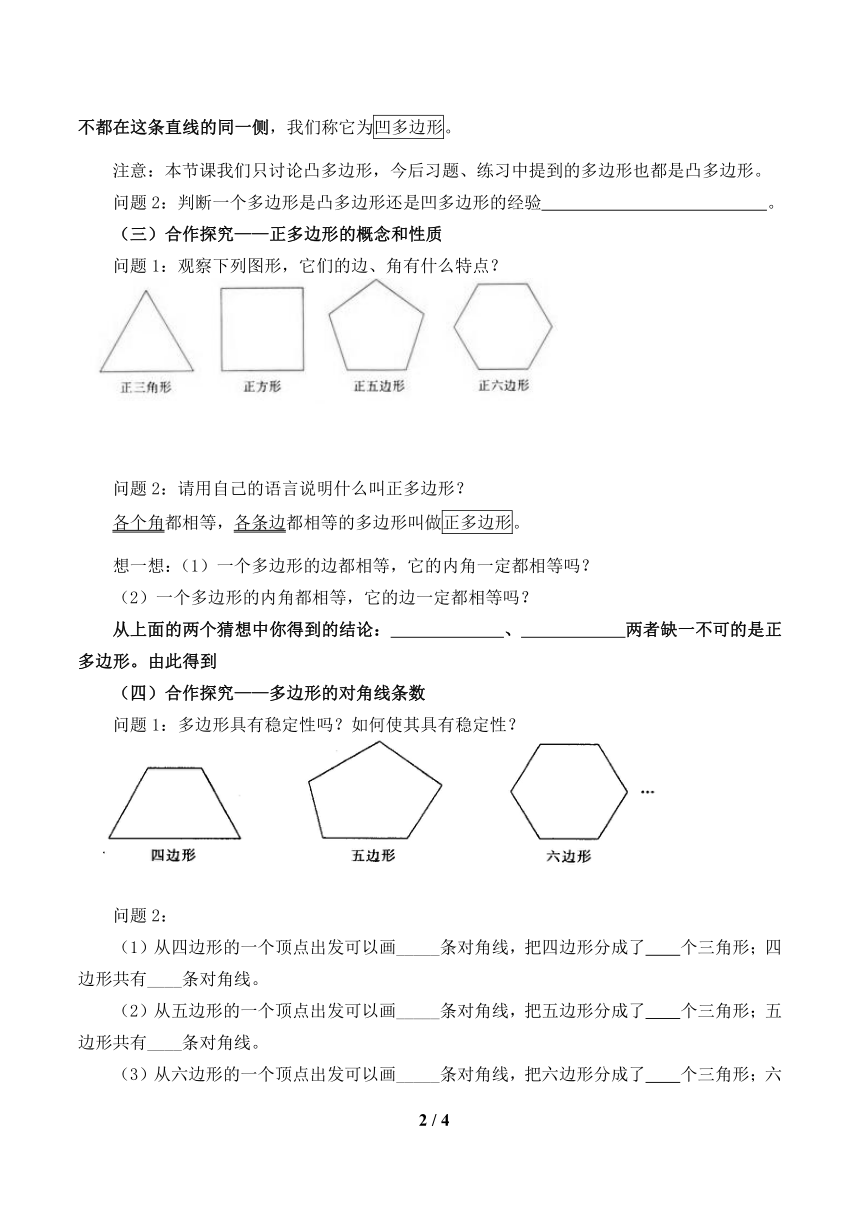
问题1:观察下列图形,它们的边、角有什么特点?
问题2:请用自己的语言说明什么叫正多边形?
各个角都相等,各条边都相等的多边形叫做正多边形。
想一想:(1)一个多边形的边都相等,它的内角一定都相等吗?
(2)一个多边形的内角都相等,它的边一定都相等吗?
从上面的两个猜想中你得到的结论: 、 两者缺一不可的是正多边形。由此得到
(四)合作探究——多边形的对角线条数
问题1:多边形具有稳定性吗?如何使其具有稳定性?
问题2:
(1)从四边形的一个顶点出发可以画_____条对角线,把四边形分成了 个三角形;四边形共有____条对角线。
(2)从五边形的一个顶点出发可以画_____条对角线,把五边形分成了 个三角形;五边形共有____条对角线。
(3)从六边形的一个顶点出发可以画_____条对角线,把六边形分成了 个三角形;六边形共有____条对角线。
问题3:
①从100边形的一个顶点出发可以画_____条对角线,把100边形分成了 个三角形;
100边形共有__ _条对角线。
②从n边形的一个顶点出发可以画____ _条对角线,把n分成了 个三角形;n边形共有___ __条对角线。
三、巩固强化
1.若过六边形的一个顶点可以画条对角线,则的值是( )
A.1 B.2 C.3 D.4
2.下列图形为正多边形的是( )
A. B. C. D.
3.如图4-2,作出正五边形的所有对角线,得到一个五角星,那么,在五角星含有的多边形中( )
A.只有三角形 B.只有三角形和四边形
C.只有三角形、四边形和五边形 D.只有三角形、四边形、五边形和六边形
4.在四边形ABCD中,的对角是( )
A. B. C. D.
5.从多边形一条边上的一点(不是顶点)处出发,连接各个顶点得到2021个三角形,则这个多边形的边数为( )
A.2023 B.2022 C.2021 D.2020
二、填空题
6.三角形共有__________条对角线,四边形共有__________条对角线,五边形共有__________条对角线,n边形共有__________条对角线.
7.画出多边形任何一条边所在直线,如果整个多边形都在直线__________,那么这个多边形称作凸多边形.
8.从某多边形的一个顶点出发,连接其余各顶点,把这个多边形分成个三角形,则这个多边形是____.
参考答案:
1.C
2.D
3.C
4.C
5.B
6. 0 2 5
7.同一侧
8.八边形.
PAGE
5 / 5
【学习目标】
1.知道多边形、多边形的内角、多边形的外角、多边形的对角线和正多边形的有关概念。
2.能够解决与多边形的对角线有关的问题。
【学习过程】
一、导入新课。
1.三角形概念: 。
2.除之前学习过的三角形外,你能找到哪些我们熟悉的图形?
二、主题探究。
(一)自主学习——类比三角形的有关概念探索多边形的有关概念
问题1:动手画一个多边形,类比三角形的概念,你能说出什么是多边形吗?
定义:在平面内,由一些线段首尾顺次相接组成的封闭图像叫做多边形。
问题2:根据图示,类比三角形的有关概念,说明什么是多边形的内角、外角和对角线
(1)多边形相邻两边组成的角叫做多边形的内角。
(2)多边形的边与它的邻边的延长线组成的角叫做多边形的外角。
(3)连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。
问题3:多边形的表示:用表示它的各个顶点的字母表示,要按定点的顺序书写,可以按顺时针或逆时针的顺序。
(二)合作探究——凸多边形和凹多边形
问题1:如图。观察这两个图形,找出相同点和不同点。
相同点:
不同点:
在图(1)中,画出四边形ABCD的任何一条边所在的直线,整个图形都在这条直线的同一侧,这样的四边形叫做凸四边形,这样的多边形称为凸多边形;
而图(2)就不满足上述凸多边形的特征,因为我们画CD(或BD)所在直线,整个多边形不都在这条直线的同一侧,我们称它为凹多边形。
注意:本节课我们只讨论凸多边形,今后习题、练习中提到的多边形也都是凸多边形。
问题2:判断一个多边形是凸多边形还是凹多边形的经验 。
(三)合作探究——正多边形的概念和性质
问题1:观察下列图形,它们的边、角有什么特点?
问题2:请用自己的语言说明什么叫正多边形?
各个角都相等,各条边都相等的多边形叫做正多边形。
想一想:(1)一个多边形的边都相等,它的内角一定都相等吗?
(2)一个多边形的内角都相等,它的边一定都相等吗?
从上面的两个猜想中你得到的结论: 、 两者缺一不可的是正多边形。由此得到
(四)合作探究——多边形的对角线条数
问题1:多边形具有稳定性吗?如何使其具有稳定性?
问题2:
(1)从四边形的一个顶点出发可以画_____条对角线,把四边形分成了 个三角形;四边形共有____条对角线。
(2)从五边形的一个顶点出发可以画_____条对角线,把五边形分成了 个三角形;五边形共有____条对角线。
(3)从六边形的一个顶点出发可以画_____条对角线,把六边形分成了 个三角形;六边形共有____条对角线。
问题3:
①从100边形的一个顶点出发可以画_____条对角线,把100边形分成了 个三角形;
100边形共有__ _条对角线。
②从n边形的一个顶点出发可以画____ _条对角线,把n分成了 个三角形;n边形共有___ __条对角线。
三、巩固强化
1.若过六边形的一个顶点可以画条对角线,则的值是( )
A.1 B.2 C.3 D.4
2.下列图形为正多边形的是( )
A. B. C. D.
3.如图4-2,作出正五边形的所有对角线,得到一个五角星,那么,在五角星含有的多边形中( )
A.只有三角形 B.只有三角形和四边形
C.只有三角形、四边形和五边形 D.只有三角形、四边形、五边形和六边形
4.在四边形ABCD中,的对角是( )
A. B. C. D.
5.从多边形一条边上的一点(不是顶点)处出发,连接各个顶点得到2021个三角形,则这个多边形的边数为( )
A.2023 B.2022 C.2021 D.2020
二、填空题
6.三角形共有__________条对角线,四边形共有__________条对角线,五边形共有__________条对角线,n边形共有__________条对角线.
7.画出多边形任何一条边所在直线,如果整个多边形都在直线__________,那么这个多边形称作凸多边形.
8.从某多边形的一个顶点出发,连接其余各顶点,把这个多边形分成个三角形,则这个多边形是____.
参考答案:
1.C
2.D
3.C
4.C
5.B
6. 0 2 5
7.同一侧
8.八边形.
PAGE
5 / 5
