北师大版七年级《数学》下册第一章第八节完全平方公式(一)说课稿[下学期]
文档属性
| 名称 | 北师大版七年级《数学》下册第一章第八节完全平方公式(一)说课稿[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 17.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-10 00:00:00 | ||
图片预览


文档简介
《完全平方公式(一)》说课稿
莆田中山中学 雍俊山
一、说教材
1、地位和作用
“完全平方公式”是义务教育北师大版七年级《数学》下册第一章第八节内容,它分为两课时,本节是第一课时,它是“整式运算”这一章中重要的内容之一,它起到承上启下的作用,既是整式相乘的应用,又为以后学习配方法打下扎实的基础。
2、课程目标:
(1)、知识目标:
经历探索推导完全平方公式的过程,形成数形结合思想,进一步发展符号感。掌握完全平方公式的结构特点,并能利用公式熟练进行运算。
(2)、能力目标:
培养学生发散性思维能力和推理能力,培养学生语言表达能力,动手实践能力,以及合作交流能力。
(3)情感目标:
让学生在探索的过程中,体会科学发现探索方法,在合作交流中,体会团结合作精神。能从多角度思考问题,敢于发表自己的观点。
3、教学重点、难点:
重点:
完全平方公式的结构特点及公式的直接运用。
难点:
对公式中a、b含义的理解与正确应用。
4、教材安排:
本节课先从通过计算和比较试验田的面积引出完全平方公式。直接让学生运用多项式乘法法则推导完全平方公式。并通过数形结合思想,让学生理解完全平方公式及其结构特点。最后通过变式训练进行练习和巩固。
二、说教学方法及教学手段:
本节课引导学生从已有的知识和生活经验出发,提出开放性的问题让学生进行合作探索,让学生经历知识的形成与应用,从而更好地理解数学知识的意义。
本节课教学中,对于不同的内容选择了不同的方法。对于求实验田的总面积,进行开放性教学,引导学生利用拼图等方法合作探究多种方法求解;运用多项式相乘推导公式,让学生独立探索;对于完全平方公式的运用,采用变式训练,促进学生灵活掌握。
为了提高课堂教学效果,本节课将借助于多媒体课件辅助教学。
三、说学法
教给学生良好的学习方法比直接教给学生知识更重要。数学教学是师生之间、学生之间交往互动与共同发展的过程,学生的学是中心,会学是目的,因此在教学中要不断指导学生学会学习,又要给学生自主探索和合作交流时间。
本节课先从实际出发,创设有助于学生发散性思考的问题情境,引导学生自己积极思考探索,让学生经历“观察、类比、发现、归纳”的过程,从而培养学生动手实践的能力,提高口头表达能力及逻辑推理能力,使学生真正成为学习的主体。
从“被动学习”变为“主动学习”。教学时先让学生动手拼图,然后观察、类比并加于归纳,从而得到完全平方公式,同时在学习中体会学习数学的乐趣。
四、教学程序设计:
(一)课前准备:课前每位同学需准备四张厚纸,规格要求如下: 一张边长为15厘米的正方形;一张边长为5厘米的正方形;两张长为15厘米、宽为5厘米的长方形。
(二)课堂教学:
教学环节 教师活动 学生活动 设计意图
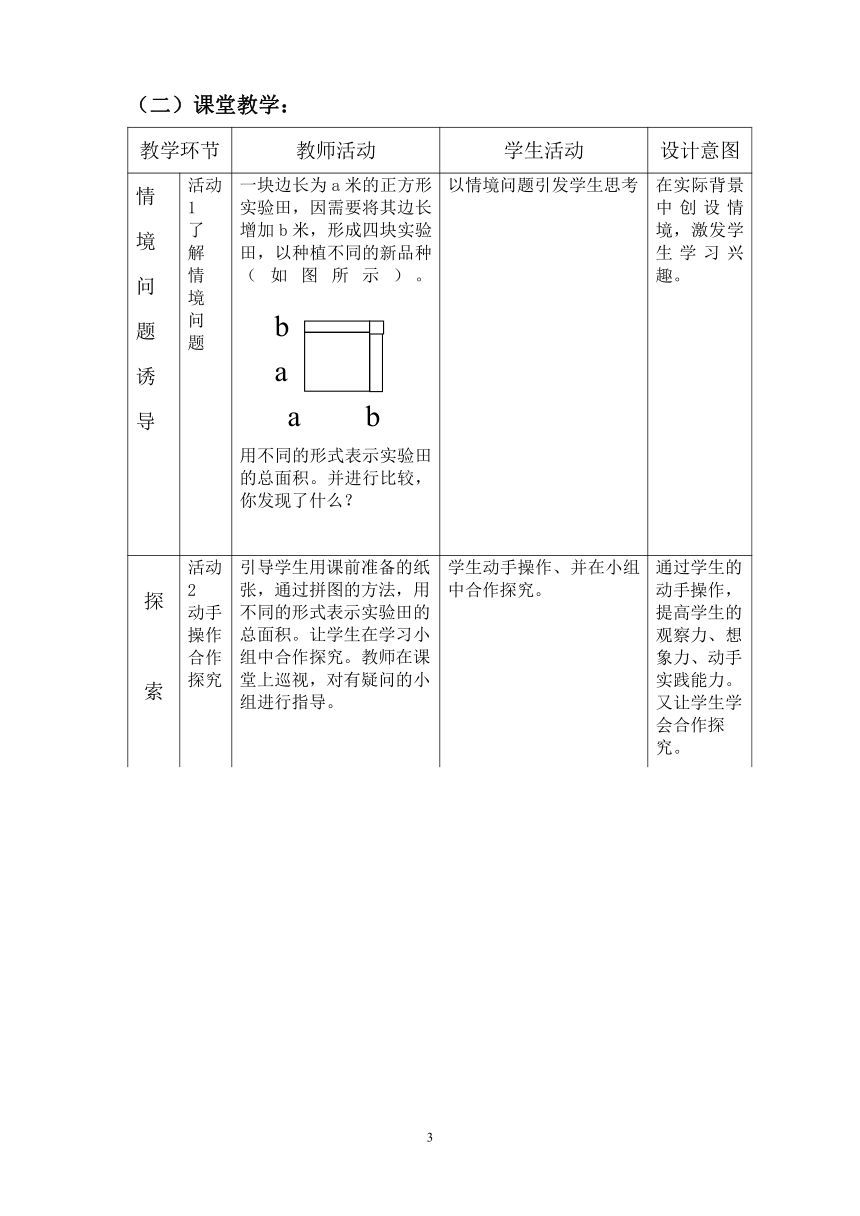
情境问题诱导 活动1了解情境问题 一块边长为a米的正方形实验田,因需要将其边长增加b米,形成四块实验田,以种植不同的新品种(如图所示)。用不同的形式表示实验田的总面积。并进行比较,你发现了什么? 以情境问题引发学生思考 在实际背景中创设情境,激发学生学习兴趣。
探索新知探索新 活动2动手操作合作探究 引导学生用课前准备的纸张,通过拼图的方法,用不同的形式表示实验田的总面积。让学生在学习小组中合作探究。教师在课堂上巡视,对有疑问的小组进行指导。 学生动手操作、并在小组中合作探究。 通过学生的动手操作,提高学生的观察力、想象力、动手实践能力。又让学生学会合作探究。
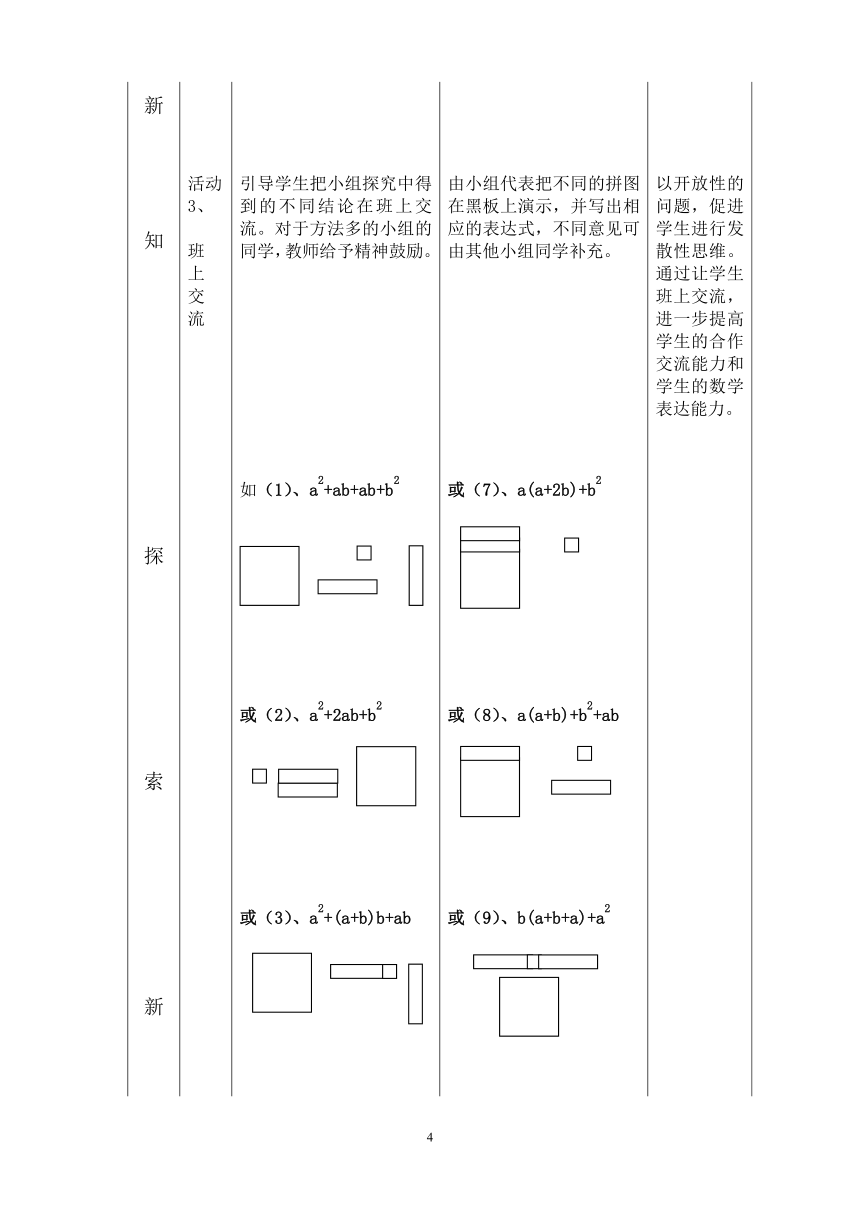
活动3、班上交流 引导学生把小组探究中得到的不同结论在班上交流。对于方法多的小组的同学,教师给予精神鼓励。 如(1)、a2+ab+ab+b2 或(2)、a2+2ab+b2或(3)、a2+(a+b)b+ab 由小组代表把不同的拼图在黑板上演示,并写出相应的表达式,不同意见可由其他小组同学补充。或(7)、a(a+2b)+b2 或(8)、a(a+b)+b2+ab或(9)、b(a+b+a)+a2 以开放性的问题,促进学生进行发散性思维。通过让学生班上交流,进一步提高学生的合作交流能力和学生的数学表达能力。
知 或(4)、b(a+b)+a(a+b)或(5)、(a+b)(a+b) 或(6)、(a+b)2 学生发现以上式子都是实验田的总面积,所以它们的表现形式不同,但最后的结果数是相等的。
探索新知 活动4自主探究 (1)、(a+b)2等于什么?引导学生用多项式乘法法则说明理由。然后,引导学生把黑板上的拼图按演算的顺序排好。教师利用多媒体演示。(1)(2)(3)(4) 让学生独立演算,请一位同学板演:解:(a+b)2=(a+b)(a+b) (1)=a(a+b)+b(a+b) (2)=a2+ab+ab+b2 (3)=a2+2ab+b2 (4)学生会惊喜发现代数演算过程与拼图的一致性。 在学生正确演算的基础上,引导学生与几何拼图的对比,从几何背景理解完全平方公式。从而,充分地让学生感受“数学的数形结合思想”。
(2)、(a-b)2等于什么?引导学生运用所学的两个数和的完全平方公式计算,小颖写出了如下算式: (a-b)2=[a+(-b)]2她是怎样想的?你觉得她的做法对吗?说明理由。如果正确,让学生自己写出算式。 老师巡视指导,对于有困难的学生给予指导帮助。 解:(a-b)2 =[a+(-b)]2 =a2+2a(-b)+(-b)2 =a2-2ab+b2 鼓励学生用自己的语言大胆表达自己的意见。
如下图,让学生用不同方法求阴影部分面积,然后 观察,不同的表达式之间的相等关系,从而检验小颖和自己的算法是否正确。 激发学生探索欲望,勇于挑战难题,提高他们的相象能力和思维能力。
归纳总结 活动5总结公式 从而我们推导了两个非常重要的公式——完全平方公式: (a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2怎样用自己的语言叙述上面的公式呢?引导学生用自己的语言叙述上面的公式。(只要学生能正确表述,教师就要给予鼓励) 先让学生在小组内讨论,然后由小组代表发言。师生总结:两数和(或差)的平方等于它们的平方和加上(或减去)它们积的2 倍。 提高学生的归纳总结能力,提高学生的口头表达能力。
实践应用 活动6例题解析 例1利用完全平方公式计算:(1)(2x-3)2 (2)(4x+5y)2教师在学生完成的基础上,利用多媒体演示解题过程。 让学生独立完成,在解题过程中理解a、b 的一般含义,经历从一般到特殊的理解过程。解:(1)( 2x - 3 )2= (2x)2-2×2x×3 + 32=4x2- 12x + 9(2)( 4x + 5y )2=(4x)2-2(4x)(5y)+ (5y)2=16x2- 40xy + 25y2 在学生独立完成的基础上,教师利用多媒体演示解题过程,以形象、生动的画面让学生能深刻理解公式,并为下面的练习作好充分的准备。
活动7变式训练 (二)、让学生利用完全平方公式编题,并在学习小组中进行交流。教师让学生把较有代表性的题目进行板演。 让学生把所编的题目在学习小组中进行交流,并互换题目进行解答及评价。 通过变式训练,有利于学生对公式的理解与应用。
总结 活动8课堂小结 让学生谈谈本节课的学习体会,如本节课我们学习了哪些内容?在探索过程中,感受到哪些成功或困惑?是否还需要帮助? 学生的回答只要有理,教师都要给予表扬。如我们学习了完全平方公式 (a±b)2=a2±2ab+b2以及公式中的a、b可以是单项式也可以是多项式;惊喜发现实验田的多种表达式以及完全平方公式的几何背景……
(三)、课后作业:
1、在自编题中选择有代表性的三道题解答;2、习题1.13第1~3;
3、思考题:计算:(a+b+c)2
(巩固加深对所学知识的理解,运用知识,形成技能、技巧,培养独立解决问题能力。)
五、主板书设计
1.8完全平方公式(一)一、完全平方公式 (a±b)2=a2±2ab+b2二、例题例1利用完全平方公式计算:(1)(2x-3)2 (2) (4x+5y)2三、学生编题 四、小结五、作业
六、评价分析
在本节课的的教学中,通过学生动手操作,教师的积极引导、启发学生探索思考,使学生学会学习、学会探索、学会合作。同时,借助多媒体课件辅助教学,极大地提高了课堂教学效果。因此,在本节课中,教师的主导性得到了较大的发挥。
学生是课堂的主人,本节课中,运用学生已有知识与学生生活密切相关的素材引入新课,学生进行了自主探索、合作交流,积极参与课堂教学,主动构建新的认知结构。同时,运用多种方法求实验田的总面积,不但增强学生学习的兴趣,而且无形中加深了他们对知识的印象,又培养了他们的发散思维能力,开辟了他们的创新精神。使学生明白,同一数学问题可以用不同的方法来解决,鼓动他们去探索一种简便的方法来解决实际中的数学问题。他们学习的积极性得到充分的发挥,因此学生和主体地位也得到很好的保证。
由于学生的个体差异表现为认知方式与思维策略的不同,以及认知水平和学习能力的差异,所以在整个教学过程中,都应尊重学生在解决问题过程中所表现出的不同水平,尽可能地让所有学生都能主动参与,并引导学生在与他人的合作交流中提高思维能力。在学生回答时,通过语言、目光、动作给予鼓励与赞许,发挥评价的积极功能。尤其注意鼓励学习有困难的学生主动参与学习活动,发表自己看法,肯定他们的点滴进步。对出现的错误耐心引导他们分析其产生的原因,鼓励他们改进;对学生思维的闪光点及时给予肯定;对学有余力并对数学有浓厚兴趣的同学,通过布置思考题去发展他们的数学才能。
在本节课的教学设计过程中,因为设计了开放性问题,部分学生的答案似乎偏离本节主题,对于这一点如何处理,还有待进一步探讨。在提倡素质教育、培养学生创新意识的今天,我觉得即使学生的回答与本节主题关系不大,但是只要讲得有理,教师都应给予肯定与鼓励,只有这样,才能真正做到激励学生大胆创新。不知我的观点是否正确,恳请各位专家赐教。
b
a
a
b
b
b
a
a
PAGE
1
莆田中山中学 雍俊山
一、说教材
1、地位和作用
“完全平方公式”是义务教育北师大版七年级《数学》下册第一章第八节内容,它分为两课时,本节是第一课时,它是“整式运算”这一章中重要的内容之一,它起到承上启下的作用,既是整式相乘的应用,又为以后学习配方法打下扎实的基础。
2、课程目标:
(1)、知识目标:
经历探索推导完全平方公式的过程,形成数形结合思想,进一步发展符号感。掌握完全平方公式的结构特点,并能利用公式熟练进行运算。
(2)、能力目标:
培养学生发散性思维能力和推理能力,培养学生语言表达能力,动手实践能力,以及合作交流能力。
(3)情感目标:
让学生在探索的过程中,体会科学发现探索方法,在合作交流中,体会团结合作精神。能从多角度思考问题,敢于发表自己的观点。
3、教学重点、难点:
重点:
完全平方公式的结构特点及公式的直接运用。
难点:
对公式中a、b含义的理解与正确应用。
4、教材安排:
本节课先从通过计算和比较试验田的面积引出完全平方公式。直接让学生运用多项式乘法法则推导完全平方公式。并通过数形结合思想,让学生理解完全平方公式及其结构特点。最后通过变式训练进行练习和巩固。
二、说教学方法及教学手段:
本节课引导学生从已有的知识和生活经验出发,提出开放性的问题让学生进行合作探索,让学生经历知识的形成与应用,从而更好地理解数学知识的意义。
本节课教学中,对于不同的内容选择了不同的方法。对于求实验田的总面积,进行开放性教学,引导学生利用拼图等方法合作探究多种方法求解;运用多项式相乘推导公式,让学生独立探索;对于完全平方公式的运用,采用变式训练,促进学生灵活掌握。
为了提高课堂教学效果,本节课将借助于多媒体课件辅助教学。
三、说学法
教给学生良好的学习方法比直接教给学生知识更重要。数学教学是师生之间、学生之间交往互动与共同发展的过程,学生的学是中心,会学是目的,因此在教学中要不断指导学生学会学习,又要给学生自主探索和合作交流时间。
本节课先从实际出发,创设有助于学生发散性思考的问题情境,引导学生自己积极思考探索,让学生经历“观察、类比、发现、归纳”的过程,从而培养学生动手实践的能力,提高口头表达能力及逻辑推理能力,使学生真正成为学习的主体。
从“被动学习”变为“主动学习”。教学时先让学生动手拼图,然后观察、类比并加于归纳,从而得到完全平方公式,同时在学习中体会学习数学的乐趣。
四、教学程序设计:
(一)课前准备:课前每位同学需准备四张厚纸,规格要求如下: 一张边长为15厘米的正方形;一张边长为5厘米的正方形;两张长为15厘米、宽为5厘米的长方形。
(二)课堂教学:
教学环节 教师活动 学生活动 设计意图
情境问题诱导 活动1了解情境问题 一块边长为a米的正方形实验田,因需要将其边长增加b米,形成四块实验田,以种植不同的新品种(如图所示)。用不同的形式表示实验田的总面积。并进行比较,你发现了什么? 以情境问题引发学生思考 在实际背景中创设情境,激发学生学习兴趣。
探索新知探索新 活动2动手操作合作探究 引导学生用课前准备的纸张,通过拼图的方法,用不同的形式表示实验田的总面积。让学生在学习小组中合作探究。教师在课堂上巡视,对有疑问的小组进行指导。 学生动手操作、并在小组中合作探究。 通过学生的动手操作,提高学生的观察力、想象力、动手实践能力。又让学生学会合作探究。
活动3、班上交流 引导学生把小组探究中得到的不同结论在班上交流。对于方法多的小组的同学,教师给予精神鼓励。 如(1)、a2+ab+ab+b2 或(2)、a2+2ab+b2或(3)、a2+(a+b)b+ab 由小组代表把不同的拼图在黑板上演示,并写出相应的表达式,不同意见可由其他小组同学补充。或(7)、a(a+2b)+b2 或(8)、a(a+b)+b2+ab或(9)、b(a+b+a)+a2 以开放性的问题,促进学生进行发散性思维。通过让学生班上交流,进一步提高学生的合作交流能力和学生的数学表达能力。
知 或(4)、b(a+b)+a(a+b)或(5)、(a+b)(a+b) 或(6)、(a+b)2 学生发现以上式子都是实验田的总面积,所以它们的表现形式不同,但最后的结果数是相等的。
探索新知 活动4自主探究 (1)、(a+b)2等于什么?引导学生用多项式乘法法则说明理由。然后,引导学生把黑板上的拼图按演算的顺序排好。教师利用多媒体演示。(1)(2)(3)(4) 让学生独立演算,请一位同学板演:解:(a+b)2=(a+b)(a+b) (1)=a(a+b)+b(a+b) (2)=a2+ab+ab+b2 (3)=a2+2ab+b2 (4)学生会惊喜发现代数演算过程与拼图的一致性。 在学生正确演算的基础上,引导学生与几何拼图的对比,从几何背景理解完全平方公式。从而,充分地让学生感受“数学的数形结合思想”。
(2)、(a-b)2等于什么?引导学生运用所学的两个数和的完全平方公式计算,小颖写出了如下算式: (a-b)2=[a+(-b)]2她是怎样想的?你觉得她的做法对吗?说明理由。如果正确,让学生自己写出算式。 老师巡视指导,对于有困难的学生给予指导帮助。 解:(a-b)2 =[a+(-b)]2 =a2+2a(-b)+(-b)2 =a2-2ab+b2 鼓励学生用自己的语言大胆表达自己的意见。
如下图,让学生用不同方法求阴影部分面积,然后 观察,不同的表达式之间的相等关系,从而检验小颖和自己的算法是否正确。 激发学生探索欲望,勇于挑战难题,提高他们的相象能力和思维能力。
归纳总结 活动5总结公式 从而我们推导了两个非常重要的公式——完全平方公式: (a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2怎样用自己的语言叙述上面的公式呢?引导学生用自己的语言叙述上面的公式。(只要学生能正确表述,教师就要给予鼓励) 先让学生在小组内讨论,然后由小组代表发言。师生总结:两数和(或差)的平方等于它们的平方和加上(或减去)它们积的2 倍。 提高学生的归纳总结能力,提高学生的口头表达能力。
实践应用 活动6例题解析 例1利用完全平方公式计算:(1)(2x-3)2 (2)(4x+5y)2教师在学生完成的基础上,利用多媒体演示解题过程。 让学生独立完成,在解题过程中理解a、b 的一般含义,经历从一般到特殊的理解过程。解:(1)( 2x - 3 )2= (2x)2-2×2x×3 + 32=4x2- 12x + 9(2)( 4x + 5y )2=(4x)2-2(4x)(5y)+ (5y)2=16x2- 40xy + 25y2 在学生独立完成的基础上,教师利用多媒体演示解题过程,以形象、生动的画面让学生能深刻理解公式,并为下面的练习作好充分的准备。
活动7变式训练 (二)、让学生利用完全平方公式编题,并在学习小组中进行交流。教师让学生把较有代表性的题目进行板演。 让学生把所编的题目在学习小组中进行交流,并互换题目进行解答及评价。 通过变式训练,有利于学生对公式的理解与应用。
总结 活动8课堂小结 让学生谈谈本节课的学习体会,如本节课我们学习了哪些内容?在探索过程中,感受到哪些成功或困惑?是否还需要帮助? 学生的回答只要有理,教师都要给予表扬。如我们学习了完全平方公式 (a±b)2=a2±2ab+b2以及公式中的a、b可以是单项式也可以是多项式;惊喜发现实验田的多种表达式以及完全平方公式的几何背景……
(三)、课后作业:
1、在自编题中选择有代表性的三道题解答;2、习题1.13第1~3;
3、思考题:计算:(a+b+c)2
(巩固加深对所学知识的理解,运用知识,形成技能、技巧,培养独立解决问题能力。)
五、主板书设计
1.8完全平方公式(一)一、完全平方公式 (a±b)2=a2±2ab+b2二、例题例1利用完全平方公式计算:(1)(2x-3)2 (2) (4x+5y)2三、学生编题 四、小结五、作业
六、评价分析
在本节课的的教学中,通过学生动手操作,教师的积极引导、启发学生探索思考,使学生学会学习、学会探索、学会合作。同时,借助多媒体课件辅助教学,极大地提高了课堂教学效果。因此,在本节课中,教师的主导性得到了较大的发挥。
学生是课堂的主人,本节课中,运用学生已有知识与学生生活密切相关的素材引入新课,学生进行了自主探索、合作交流,积极参与课堂教学,主动构建新的认知结构。同时,运用多种方法求实验田的总面积,不但增强学生学习的兴趣,而且无形中加深了他们对知识的印象,又培养了他们的发散思维能力,开辟了他们的创新精神。使学生明白,同一数学问题可以用不同的方法来解决,鼓动他们去探索一种简便的方法来解决实际中的数学问题。他们学习的积极性得到充分的发挥,因此学生和主体地位也得到很好的保证。
由于学生的个体差异表现为认知方式与思维策略的不同,以及认知水平和学习能力的差异,所以在整个教学过程中,都应尊重学生在解决问题过程中所表现出的不同水平,尽可能地让所有学生都能主动参与,并引导学生在与他人的合作交流中提高思维能力。在学生回答时,通过语言、目光、动作给予鼓励与赞许,发挥评价的积极功能。尤其注意鼓励学习有困难的学生主动参与学习活动,发表自己看法,肯定他们的点滴进步。对出现的错误耐心引导他们分析其产生的原因,鼓励他们改进;对学生思维的闪光点及时给予肯定;对学有余力并对数学有浓厚兴趣的同学,通过布置思考题去发展他们的数学才能。
在本节课的教学设计过程中,因为设计了开放性问题,部分学生的答案似乎偏离本节主题,对于这一点如何处理,还有待进一步探讨。在提倡素质教育、培养学生创新意识的今天,我觉得即使学生的回答与本节主题关系不大,但是只要讲得有理,教师都应给予肯定与鼓励,只有这样,才能真正做到激励学生大胆创新。不知我的观点是否正确,恳请各位专家赐教。
b
a
a
b
b
b
a
a
PAGE
1
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
