1.3 反比例函数的应用 课件(共29张PPT)
文档属性
| 名称 | 1.3 反比例函数的应用 课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-18 20:32:26 | ||
图片预览








文档简介
(共29张PPT)
湘教版数学九年级
2022秋精品课件
1.3 反比例函数的应用
对现实生活中的许多问题,我们都可以通过建立反比例函数模型来加以解决
某科技小组在一次野外考察途中遇到一片烂泥湿地.
为了安全、迅速地通过这片湿地,他们沿着前进路线铺
垫了若干块木板,构筑成一条临时通道,从而顺利通过了这片湿地.
动脑筋
(1)根据压力F(N)、压强 p(Pa)与受力面积 S( )
之间的关系式 ,请你判断:当F一定时,p是S
的反比例函数吗?
解 对于 ,当F一定时,根据反比例函数的定义
可知,p是S的反比例函数.
(2) 若人对地面的压力 F=450N, 完成下表:
受力面积S( ) 0.005 0.01 0.02 0.04
压强p(Pa)
当S = 0.02 时,p=22500 Pa;
当S = 0.04 时,p =11250 Pa.
类似地,当S = 0.01 时,p= 45000 Pa;
(Pa).
所以当S =0.005 时,由 ,得
解
因为F = 450N,
(3)当F=450N时,试画出该函数的图象,并结合图
象分析当受力面积S增大时,地面所受压强p是
如何变化的.据此请说出他们铺垫木板(木板
重力忽略不计)通过湿地的道理.
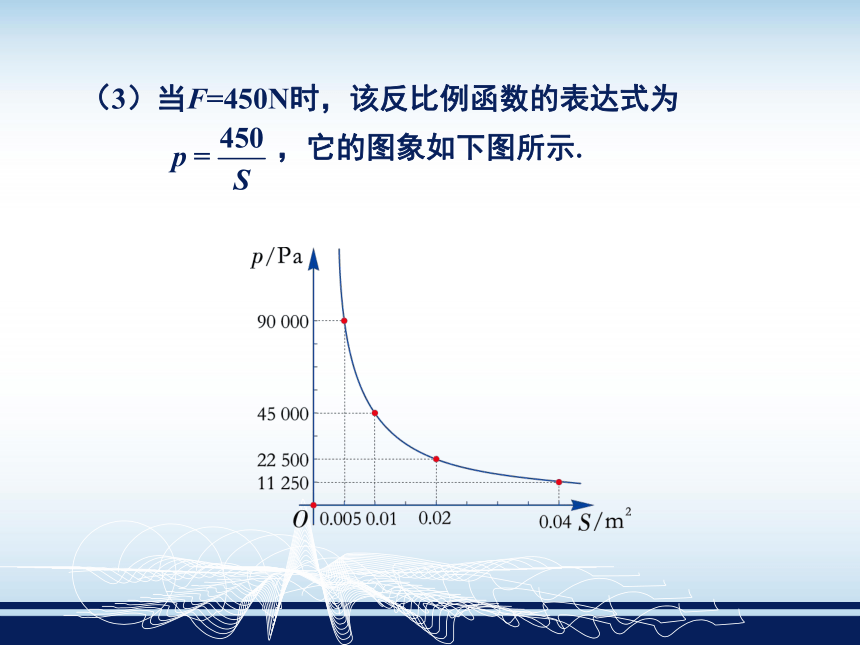
(3)当F=450N时,该反比例函数的表达式为
,它的图象如下图所示.
由图象的性质可知,当受力面积S增大时,地面所受压强p会越来越小.因此,该科技小组通过铺垫木板的方法来增大受力面积,以减小地面所受压强,从而可以顺利地通过湿地.
你能根据波义耳定律(在温度不变的情况下,气体的压强P与它的体积V的乘积是一个常数k(k>0),即pV=k)来解释:为什么使劲踩气球时,气球会爆炸?
议一议
议一议
议一议
例
已知某电路的电压U(V)、电流I(A)、电阻R(Ω)三者之间有如下关系式:U=I R,且该电路的电压U恒为220V.
举
例
分析 由于该电路的电压U为定值,即该电路的电阻R 与电流I的乘积为定值,因此该电路的电阻R与电流I成反比例关系.
(1)写出电流 I 关于电阻 R 的函数表达式;
解 因为U=IR,且U=220V,所以IR=220,即该电路
的电流I关于电阻R的函数表达式为 .
(2)如果该电路的电阻为200Ω,则通过它的电流是多少?
解 因为该电路的电阻R = 200Ω,所以通过该电路
的电流 = 1.1(A).
(A).
(3)如果该电路接入的是一个滑动变阻器,怎样调整
电阻R ,就可以使电路中的电流I增大?
解
根据反比例函数 的图象(如下图所示)及性质可知,当滑动变阻器的电阻R减小时,就可以使电路中的电流I增大.
1.举例说明反比例函数在生活中的应用.
练习
答:生活中使劲踩气球时,气球会爆炸: 在温度不变的情况下,气球内气体的压强p与它的体积V的乘积是一个常数k;纳鞋底时要用锥子,当用力一定时,锥子接触鞋底的面积比铁棍等小许多,对鞋底产生的压强很大,鞋底就容易纳了.
2.某天然气公司要在地下修建一个容积为 的圆柱形天然气储存室.
(1)储存室的底面积S( )与其深度d(m)有怎样的函数关系?
(2)若公司决定把储存室的底面积S定为5000 ,则施工队施工时应该向下掘进多深?
(3)当施工队按(2)中的计划掘进到地下15m时,碰上了坚硬的岩石,为了节约建设资金,公司决定把储存室的深度改为15m ,则相应地储存室的底面积应改为多少才能满足需要?(精确到0.01 )
储存室的底面积S( )与其深度d(m)有怎样的函数关系?
(1)
解
(d>0).
(2)若公司决定把储存室的底面积S定为5000 ,
则施工队施工时应该向下掘进多深?
解
中
时:
(m).
当施工队按(2)中的计划掘进到地下15m时,
碰上了坚硬的岩石,为了节约建设资金,公司
决定把储存室的深度改为15m,则相应地储存
室的底面积应改为多少才能满足需要
(精确到0.01 )?
(3)
时:
中
解
中
解
中考试题
某气球内充满了一定质量的气体,当温度
不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气
球内的气压大于120kPa时,气球将爆炸. 为了
安全起见,气球的体积应( )
A. 不大于 B. 小于
C. 不小于 D. 大于
C
例
解析
由题意设P与V的函数关系式为 (k≠0),
将(1.6,60)代入上式得k=96. 即 .
又∵P≤120时,气球安全,
∴ ,
∴
故选C.
1. 举例说明什么是反比例函数.
2. 分别画出当k>0,k<0时,反比例函数 (k为常数)
的大致图象,并说说反比例函数图象的性质.
3. 你能举出生活中应用反比例函数的实例吗?
小结与复习
1. 举例说明什么是反比例函数.
2. 分别画出当k>0,k<0时,反比例函数 (k为常数)
的大致图象,并说说反比例函数图象的性质.
3. 你能举出生活中应用反比例函数的实例吗?
实际问题
建立反比例函数模型
反比例函数的图象与性质
反比例函数的应用
1.
学习本章时,应注意从概念、图象和性质等各方面
对正比例函数和反比例函数进行研究比较,以形成
对“比例”函数的完整认识.
在学习反比例函数 (k ≠ 0)的图象与性质时,要注意从k>0,k<0 两种情况来讨论,从而全面掌
握反比例函数的图象与性质.
2.
3.
反比例函数 由比例系数k决定,自变量与对应函数值的乘积都等于k ,因此知道函数图象上一点的坐标,就能求出k ,进而确定一个反比例函数的表达式.
(k ≠ 0)
在利用反比例函数解决某些实际问题时,可利用反比例函数的图象与性质来说明.
4.
结 束
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
湘教版数学九年级
2022秋精品课件
1.3 反比例函数的应用
对现实生活中的许多问题,我们都可以通过建立反比例函数模型来加以解决
某科技小组在一次野外考察途中遇到一片烂泥湿地.
为了安全、迅速地通过这片湿地,他们沿着前进路线铺
垫了若干块木板,构筑成一条临时通道,从而顺利通过了这片湿地.
动脑筋
(1)根据压力F(N)、压强 p(Pa)与受力面积 S( )
之间的关系式 ,请你判断:当F一定时,p是S
的反比例函数吗?
解 对于 ,当F一定时,根据反比例函数的定义
可知,p是S的反比例函数.
(2) 若人对地面的压力 F=450N, 完成下表:
受力面积S( ) 0.005 0.01 0.02 0.04
压强p(Pa)
当S = 0.02 时,p=22500 Pa;
当S = 0.04 时,p =11250 Pa.
类似地,当S = 0.01 时,p= 45000 Pa;
(Pa).
所以当S =0.005 时,由 ,得
解
因为F = 450N,
(3)当F=450N时,试画出该函数的图象,并结合图
象分析当受力面积S增大时,地面所受压强p是
如何变化的.据此请说出他们铺垫木板(木板
重力忽略不计)通过湿地的道理.
(3)当F=450N时,该反比例函数的表达式为
,它的图象如下图所示.
由图象的性质可知,当受力面积S增大时,地面所受压强p会越来越小.因此,该科技小组通过铺垫木板的方法来增大受力面积,以减小地面所受压强,从而可以顺利地通过湿地.
你能根据波义耳定律(在温度不变的情况下,气体的压强P与它的体积V的乘积是一个常数k(k>0),即pV=k)来解释:为什么使劲踩气球时,气球会爆炸?
议一议
议一议
议一议
例
已知某电路的电压U(V)、电流I(A)、电阻R(Ω)三者之间有如下关系式:U=I R,且该电路的电压U恒为220V.
举
例
分析 由于该电路的电压U为定值,即该电路的电阻R 与电流I的乘积为定值,因此该电路的电阻R与电流I成反比例关系.
(1)写出电流 I 关于电阻 R 的函数表达式;
解 因为U=IR,且U=220V,所以IR=220,即该电路
的电流I关于电阻R的函数表达式为 .
(2)如果该电路的电阻为200Ω,则通过它的电流是多少?
解 因为该电路的电阻R = 200Ω,所以通过该电路
的电流 = 1.1(A).
(A).
(3)如果该电路接入的是一个滑动变阻器,怎样调整
电阻R ,就可以使电路中的电流I增大?
解
根据反比例函数 的图象(如下图所示)及性质可知,当滑动变阻器的电阻R减小时,就可以使电路中的电流I增大.
1.举例说明反比例函数在生活中的应用.
练习
答:生活中使劲踩气球时,气球会爆炸: 在温度不变的情况下,气球内气体的压强p与它的体积V的乘积是一个常数k;纳鞋底时要用锥子,当用力一定时,锥子接触鞋底的面积比铁棍等小许多,对鞋底产生的压强很大,鞋底就容易纳了.
2.某天然气公司要在地下修建一个容积为 的圆柱形天然气储存室.
(1)储存室的底面积S( )与其深度d(m)有怎样的函数关系?
(2)若公司决定把储存室的底面积S定为5000 ,则施工队施工时应该向下掘进多深?
(3)当施工队按(2)中的计划掘进到地下15m时,碰上了坚硬的岩石,为了节约建设资金,公司决定把储存室的深度改为15m ,则相应地储存室的底面积应改为多少才能满足需要?(精确到0.01 )
储存室的底面积S( )与其深度d(m)有怎样的函数关系?
(1)
解
(d>0).
(2)若公司决定把储存室的底面积S定为5000 ,
则施工队施工时应该向下掘进多深?
解
中
时:
(m).
当施工队按(2)中的计划掘进到地下15m时,
碰上了坚硬的岩石,为了节约建设资金,公司
决定把储存室的深度改为15m,则相应地储存
室的底面积应改为多少才能满足需要
(精确到0.01 )?
(3)
时:
中
解
中
解
中考试题
某气球内充满了一定质量的气体,当温度
不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气
球内的气压大于120kPa时,气球将爆炸. 为了
安全起见,气球的体积应( )
A. 不大于 B. 小于
C. 不小于 D. 大于
C
例
解析
由题意设P与V的函数关系式为 (k≠0),
将(1.6,60)代入上式得k=96. 即 .
又∵P≤120时,气球安全,
∴ ,
∴
故选C.
1. 举例说明什么是反比例函数.
2. 分别画出当k>0,k<0时,反比例函数 (k为常数)
的大致图象,并说说反比例函数图象的性质.
3. 你能举出生活中应用反比例函数的实例吗?
小结与复习
1. 举例说明什么是反比例函数.
2. 分别画出当k>0,k<0时,反比例函数 (k为常数)
的大致图象,并说说反比例函数图象的性质.
3. 你能举出生活中应用反比例函数的实例吗?
实际问题
建立反比例函数模型
反比例函数的图象与性质
反比例函数的应用
1.
学习本章时,应注意从概念、图象和性质等各方面
对正比例函数和反比例函数进行研究比较,以形成
对“比例”函数的完整认识.
在学习反比例函数 (k ≠ 0)的图象与性质时,要注意从k>0,k<0 两种情况来讨论,从而全面掌
握反比例函数的图象与性质.
2.
3.
反比例函数 由比例系数k决定,自变量与对应函数值的乘积都等于k ,因此知道函数图象上一点的坐标,就能求出k ,进而确定一个反比例函数的表达式.
(k ≠ 0)
在利用反比例函数解决某些实际问题时,可利用反比例函数的图象与性质来说明.
4.
结 束
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
