平行线的特征[上学期]

课件21张PPT。平行线的特征1.同位角相等，两直线平行.
2.内错角相等，两直线平行.
3.同旁内角互补，两直线平行.如果两直线平行，那么同位角、内错角、同旁内角的又会有怎样的关系呢？1.两直线平行，同位角相等.
2.两直线平行，内错角相等.
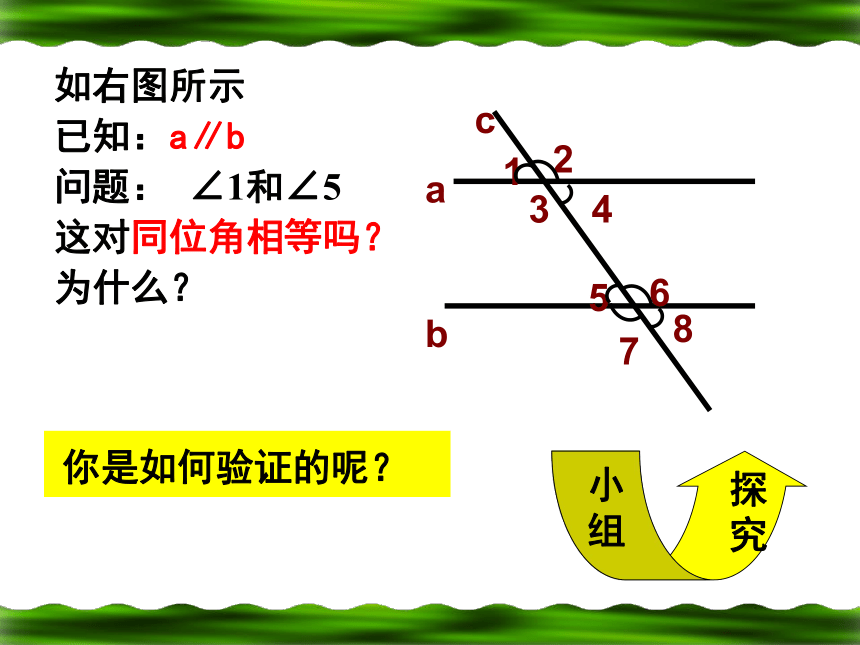
3.两直线平行，同旁内角互补.如右图所示
已知：a∥b
问题： ∠1和∠5
这对同位角相等吗？
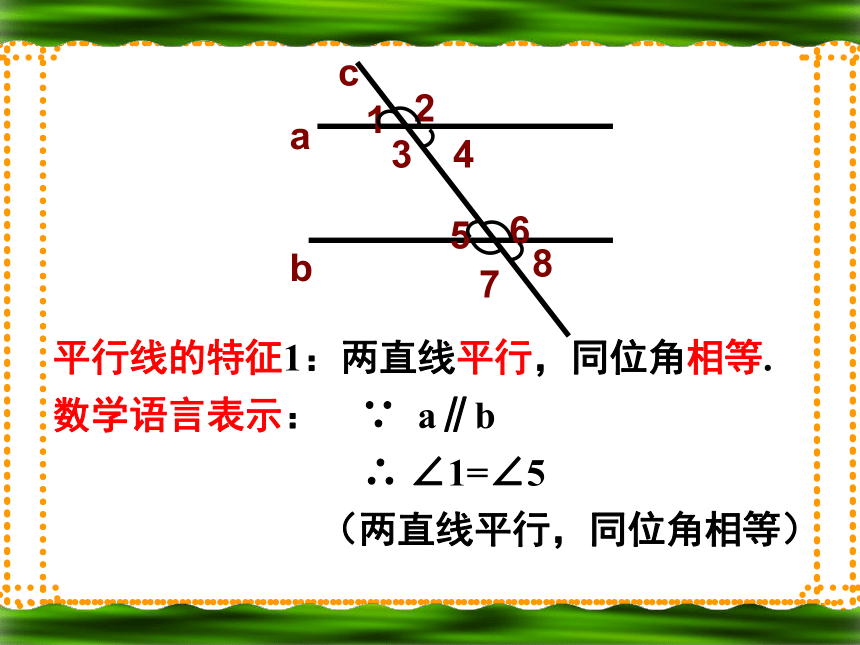
为什么？ 你是如何验证的呢？平行线的特征1：两直线平行，同位角相等.
数学语言表示： ∵ a∥b
∴ ∠1=∠5
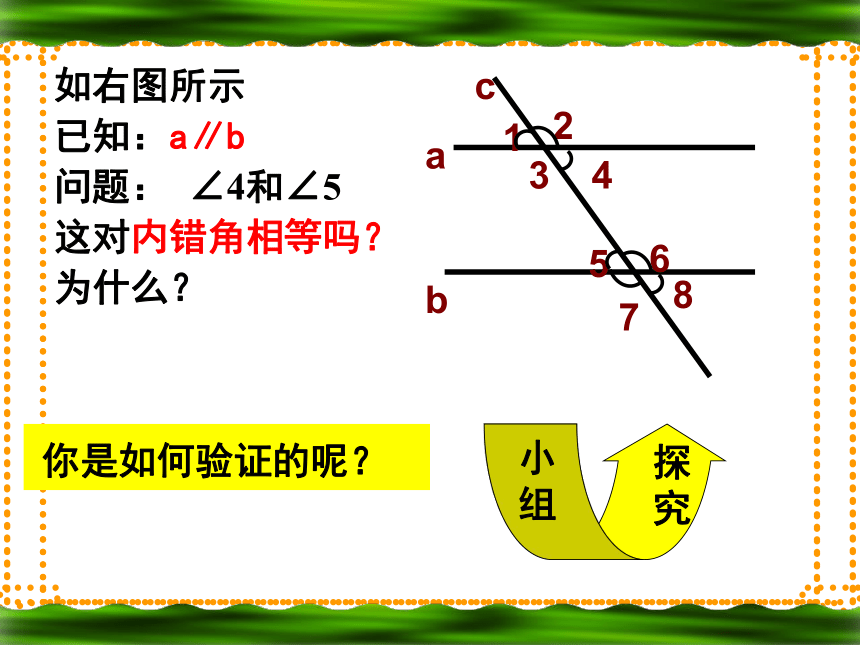
（两直线平行，同位角相等）如右图所示
已知：a∥b
问题： ∠4和∠5
这对内错角相等吗？
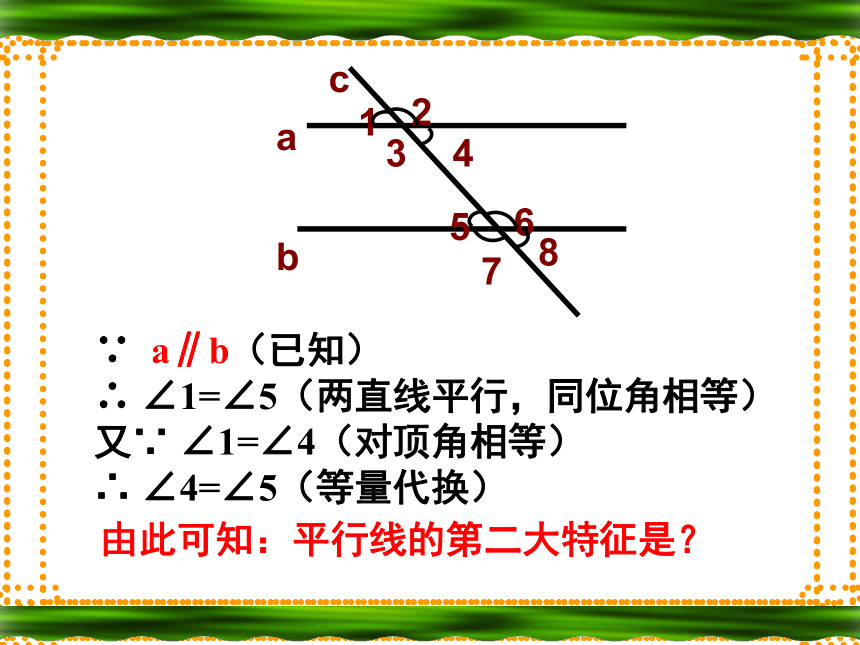
为什么？ 你是如何验证的呢？∵ a∥b（已知）
∴ ∠1=∠5（两直线平行，同位角相等）
又∵ ∠1=∠4（对顶角相等）
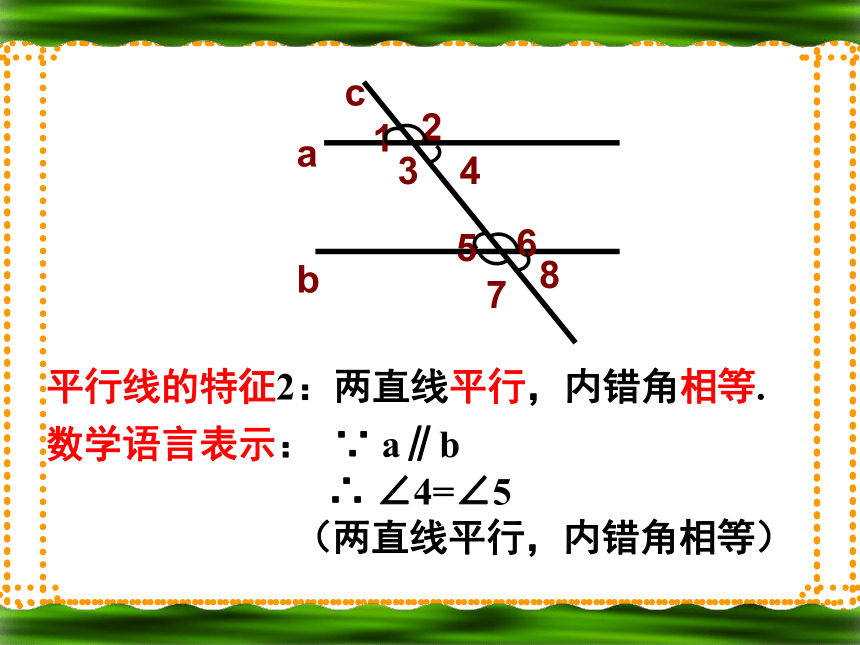
∴ ∠4=∠5（等量代换）由此可知：平行线的第二大特征是？平行线的特征2：两直线平行，内错角相等.
数学语言表示： ∵ a∥b
∴ ∠4=∠5
（两直线平行，内错角相等）如右图所示
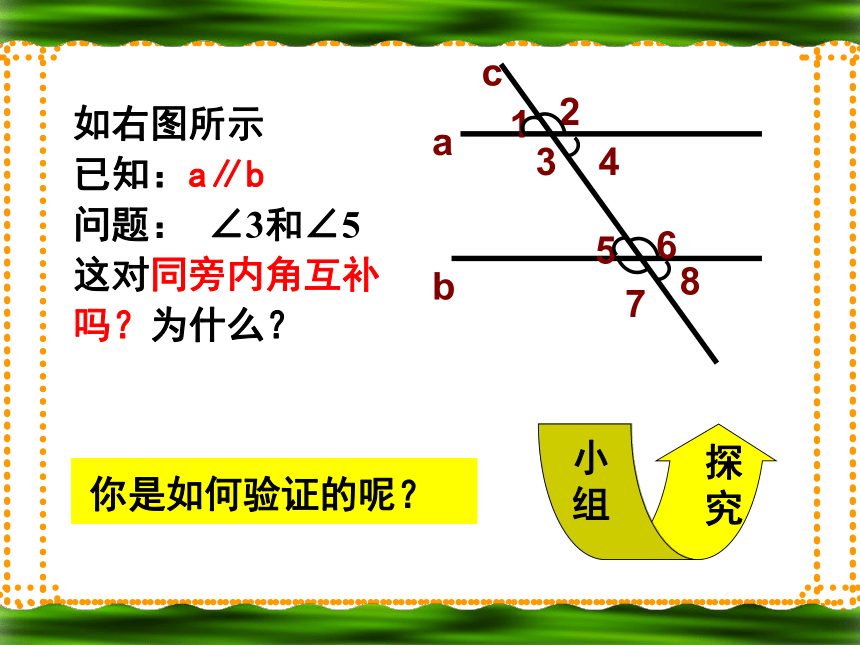
已知：a∥b
问题： ∠3和∠5
这对同旁内角互补
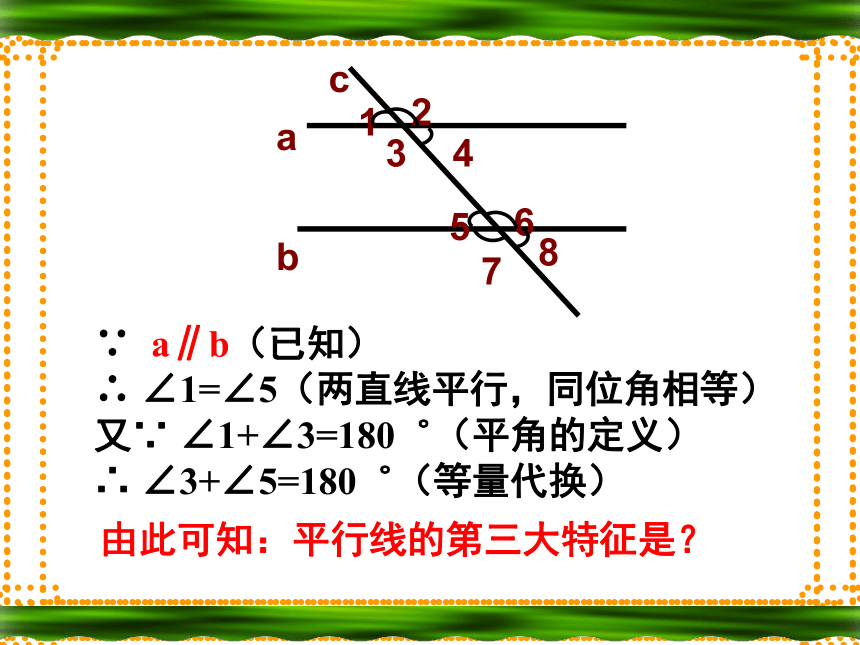
吗？为什么？ 你是如何验证的呢？∵ a∥b（已知）
∴ ∠1=∠5（两直线平行，同位角相等）
又∵ ∠1+∠3=180゜（平角的定义）
∴ ∠3+∠5=180゜（等量代换）由此可知：平行线的第三大特征是？平行线的特征3：两直线平行，同旁内角互补.数学语言表示： ∵ a∥b
∴ ∠3+∠5=180゜
（两直线平行， 同旁内角互补）验证平行线三大特征的方法？度量法 叠合法 推理法数学就在身边如图，一条公路两次拐弯后，仍保持原来的方向，第一次拐的角度 是144°，第二次拐的角度 是多少度？为什么？1440两直线平行，
内错角相等。小明用吸管喝饮料时，吸管
在饮料中的位置如图所示，
如果∠ 1=75°，
则∠2=_____
(饮料罐的上下底面互相平行)105°34甲、乙两工程队分别从两条平行的公路的A,B两点开工，铺设一条自来水管，在A处测得水管方向为北偏东42°，那么乙在B处沿怎样方向施工才能铺设成功？南偏西42°考考你你知道三星堆遗址吗？位置：四川省
面积：12平方公里，
距今：4800年至2800年，　　
出土了各种文物：金器、玉器、石器、陶器、青铜器...等数千件。
其中：有享誉中外的金杖、金面罩、
青铜人像、头像、人立像、画具等
精品文物1000多件。一块梯形的残缺玉片，你
能求出残缺角的度数吗？BC想一想？请同学思考讨论1分钟，然后说说自己对本节课
的体会。包括：“ 错误诊断” “ 我的发现”等
探求平行线平行的条件与平行线平行的特征有何异同？直线平行位置关系角与角的数量关系角与角的数量关系直线平行位置关系特征判定特征BACDE如图，AB//CD，你知道∠B+ ∠D+ ∠BED是多大吗？你能说明理由吗？答：360度。
过E做AB的
平行线EF。F挑战难题：谢谢指导，
再见！