北师大版七下平行线的特征课件[下学期]

(共16张PPT)
QQ:413097092
如何判断两直线平行？你有什么方法？
同位角相等，两直线平行。
内错角相等，两直线平行。
同旁内角互补，两直线平行。
平行线的特征
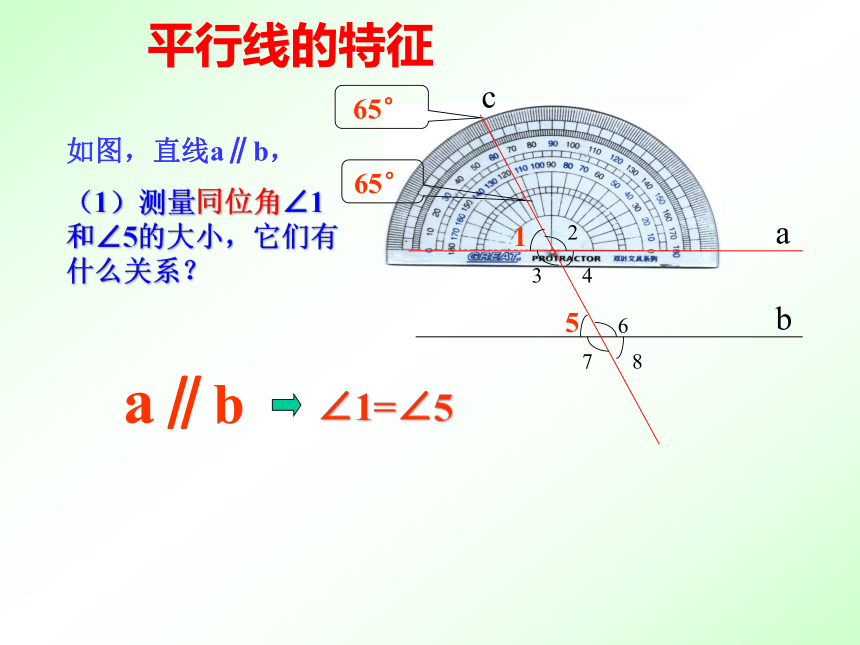
如图，直线a∥b，
（1）测量同位角∠1和∠5的大小，它们有什么关系？
65°
65°
c
a
b
1
5
2
3
4
6
7
8
∠1=∠5
a∥b
1
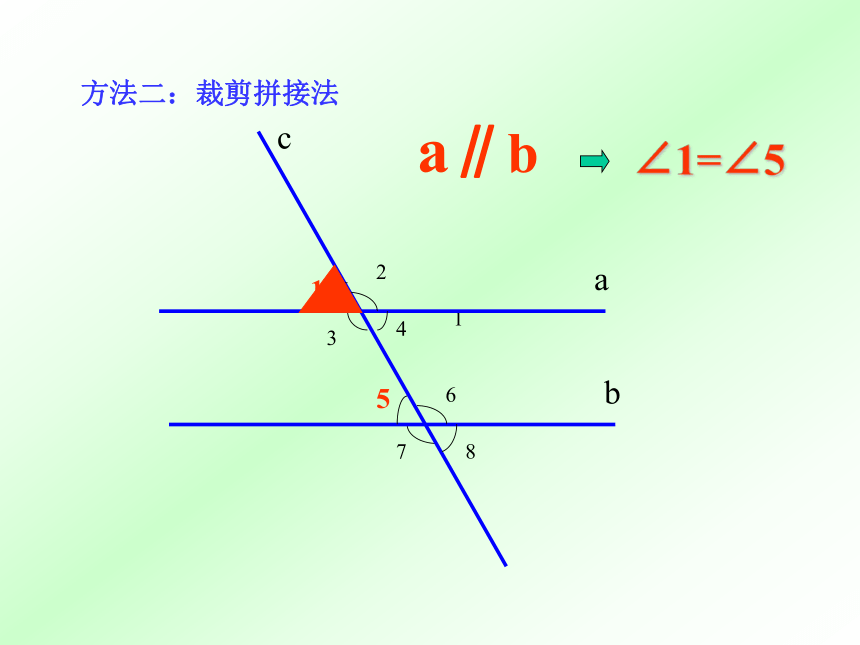
方法二：裁剪拼接法
b
5
6
8
a
c
2
3
4
7
1
∠1=∠5
a∥b
平行线的特征
如图，a∥b，
（1）测量同位角∠1和∠5的大小，它们有什么关系？
c
a
b
1
5
2
3
4
6
7
8
∠1=∠5
图中还有其它同位角吗？
它们的大小有什么关系？
∠2=∠6
∠3=∠7
∠4=∠8
由此得到：两直线平行，同位角相等
a∥b
（2）图中有几对内错角？它们的大小有什么关系？为什么？
∠3=∠6
∠4=∠5
1
b
5
6
8
a
c
2
3
4
7
a∥b
由此得：两直线平行，内错角相等
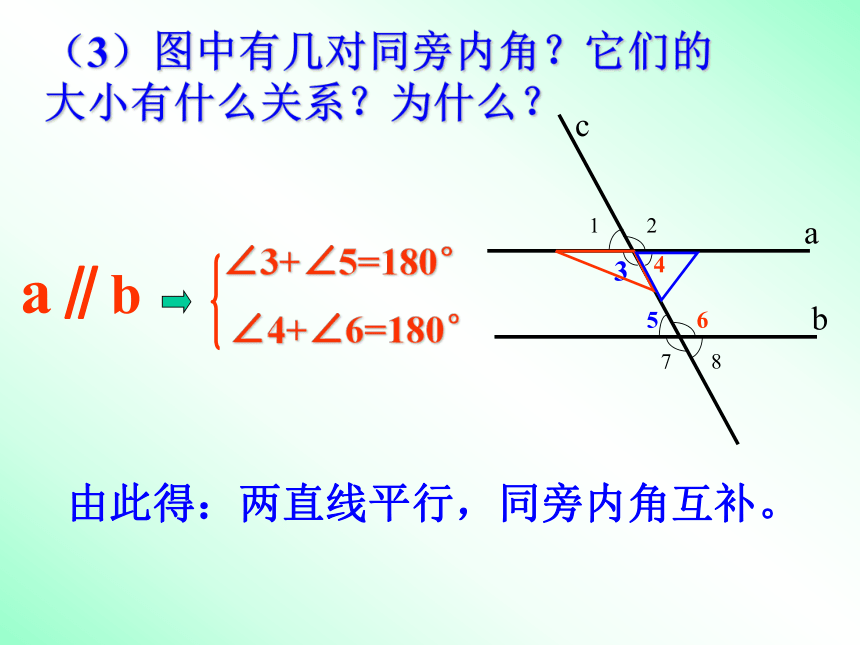
（3）图中有几对同旁内角？它们的大小有什么关系？为什么？
∠4+∠6=180°
∠3+∠5=180°
b
5
6
8
a
c
2
3
4
7
1
a∥b
由此得：两直线平行，同旁内角互补。
两直线平行，内错角相等。
两直线平行，同旁内角互补。
两直线平行，同位角相等。
同位角相等，两直线平行
内错角相等，两直线平行
同旁内角互补，两直线平行
你记
清楚了吗？
上节结论
A
D
C
B
1
6
5
4
3
2
7
8
14
13
15
16
10
9
11
12
1、如图所示 AB∥CD, AC∥BD.分
别找出与∠1相等或互补的角。
解：
∠1 =∠3
=∠5
=∠7
=∠9
=∠11
=∠13
=∠15
∠1 +∠2 = ∠1 + ∠4 = ∠1 + ∠6 = ∠1 + ∠8 = ∠1 + ∠10 = ∠1 + ∠12 = ∠1 + ∠14 = ∠1 + ∠16 =180°
2.如图a∥b，c ∥d，
∠１=60°,
那么 ①∠2=____
②∠3=____
③ ∠4=____
④ ∠5=____
120°
60°
60°
60°
a
2
b
60°
d
1
5
3
4
c
3.如图 AB∥CD，∠α=45°，∠D=∠C
那么∠ D= ，
∠C= ，
∠ B= 。
A
B
C
D
α
45°
60 °
A
B
C
D
E
F
1
2
60 °
4.如图 AB∥CD， CD ∥EF，
∠1 = ∠2=60 ° ，那么
∠A= ，
∠E= 。
45°
45°
135°
120 °
120 °
如图：一束平行光线AB和DE射向一个水平镜面后被发射，此时∠1=∠2 ， ∠3=∠4 。
1
2
3
4
B
E
A
C
D
F
（1 ）∠1___∠3
∠2___∠4
（2 ）发射光线BC与EF也平行吗？
？
=
？
=
∵ ∠2=∠4
BC∥EF
同位角相等两直线平行
两直线平行
同位角相等
潜望镜中的两个镜子MN、EF是平行放置的，光线经过镜子反射时，∠1=∠2，∠3=∠4，请说明为什么进入潜望镜的光线AB和离开潜望镜的光线CD是平行的
F
1
2
3
4
A
B
C
D
M
N
E
5
6
第一个算出地球周长的人
2000多年前，有人用简单的测量工具计算出地球的周长。这个人就是古希腊的爱拉斯托塞。 爱拉斯托塞博学多才。
细心的爱拉斯托塞发现：离亚历山大城A约785公里的塞尼城S，夏日正午的阳光可以一直照到井底，也就是说,在那一时刻,太阳正好悬挂在塞尼城的正上方E,阳光能够只指地心O.而在此时他所在的亚历山大城阳光却不能直接射到水井的底部.爱拉斯托塞在地上竖起一根小
木棍AC,测量天顶方向AB与太阳方向AD之间的夹角∠1,发现这个夹角等于360°的1/50 .
E
D
B
1
S
A
O
2
C
E
D
B
1
S
A
O
2
C
由于太阳离地球非常遥远,把射到地球上的阳光看作是彼此平行的,
即AD ∥SE,所以∠１= ∠2.
两直线平行，同位角相等。
那么∠2的度数也等于360°的1/50 ,所以,亚历山大城到塞尼城的距离弧AS也等于整个地球周长的1/50 .而亚历山大城到塞尼城的距离约为785公里,785×50=369250公里,这是一个相当精确的结果.