24.1.1圆的有关概念
文档属性
| 名称 | 24.1.1圆的有关概念 |  | |
| 格式 | zip | ||
| 文件大小 | 699.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-14 20:17:26 | ||
图片预览











文档简介
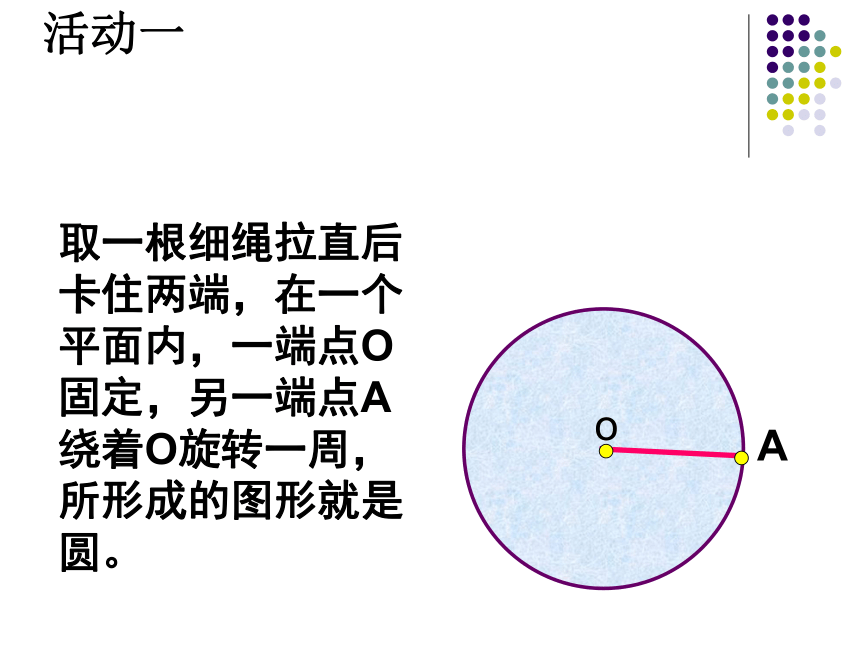
课件47张PPT。24.1.1圆的有关概念圆圆生活剪影一石激起千层浪奥运五环福建土楼乐在其中小憩片刻祥子一、 创设情境 引入新课取一根细绳拉直后卡住两端,在一个平面内,一端点O固定,另一端点A绕着O旋转一周,所形成的图形就是圆。活动一 .活动2 观察下列画圆的过程,你能由此说出圆的形成过程吗?.在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的封闭曲线叫做圆圆的定义:圆心半径记作:读作:圆O⊙O·rOA 圆心:固定的端点O叫做圆心; 半径:线段OA叫做半径;圆具有的特征:(1)圆上各点到定点(圆心O)
的距离都等于定长(半径r);同圆内 半径有无数条 长度都相等(2)到定点的距离都等于定长
的点都在同一个圆上.圆具有的特征:思考?圆的大小、位置与什么有关系?
圆心确定圆的位置,半径确定圆的大小.注意: 要确定一个圆,必须确定圆的____和____ .圆心半径注意: 根据圆的定义,“圆”指的是“ 圆周 ”,而不是“圆面”。注意: 车轮为什么做成圆形?应 用 新 知骆驼祥子把车轮做成圆形,车轮上各点到车轮中心(圆心)
的距离都等于车轮的半径,
当车轮在平面上滚动时,
车轮中心与平面的距离
保持不变。因此,
当车辆在平坦的路上行使时,
坐车的人会感觉到非常平稳,
这也是车轮都做成圆形的
数学道理。结论:思考:你能说出为什么车轮不弄成正方形?点和圆的位置关系 爱好运动的小华、小强、小兵三人相邀搞一次掷飞镖比赛。他们把靶子钉在一面土墙上,规则是谁掷出落点离红心越近,谁就胜。如下图中A、B、C三点分别是他们三人某一轮掷镖的落点,你认为这一轮中谁的成绩好? ABC 如图,设⊙O 的半径为r,A点在圆内,
B点在圆上,C点在圆外,那么点A在⊙O内 点B在⊙O上 点C在⊙O外 OA<r, OB=r, OC>r. 反过来也成立,如果已知点到圆心的距离和圆的半径的关系,就可以判断点和圆的位置关系。 OA<r OB=r OC>r设⊙O 的半径为r,点P到圆心的距离OP=d,则有:点P在⊙O内 点P在⊙O上 点P在⊙O外 d<r d=r d>rd圆外的点圆内的点圆上的点 平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点。 圆的内部可以看成是到圆心的距离小于半径的点的集合;圆的外部可以看成是 。到圆心的距离大于半径的点的集合思考:平面上的一个圆把平面上的点分成哪几部分?练一练 1、⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 。 2、⊙O的半径6cm,当OP=6时,点P在 ;当OP 时点P在圆内;当OP 时,点P不在圆外。圆内圆上圆外圆上<6≤6 这节课你学到了哪些知识?有什么感想?课堂小结:定义一: 在同一平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫圆。固定的端点O叫做圆心,线段OA叫做半径。1、从运动和集合的观点理解圆的定义:定义二:圆是到定点的距离等于定长的点的集合。3、证明几个点在同一个圆上的方法。 要证明几个点在同一个圆上,只要证明这几个点与一个定点的距离相等。2、点与圆的位置关系:设⊙O的半径为r,则点P与⊙O的位置关系有:(1)点P在⊙O上 OP=r(2)点P在⊙O内 OP<r(3)点P在⊙O外 OP>r作业:再 见课后练习1,2,3
的距离都等于定长(半径r);同圆内 半径有无数条 长度都相等(2)到定点的距离都等于定长
的点都在同一个圆上.圆具有的特征:思考?圆的大小、位置与什么有关系?
圆心确定圆的位置,半径确定圆的大小.注意: 要确定一个圆,必须确定圆的____和____ .圆心半径注意: 根据圆的定义,“圆”指的是“ 圆周 ”,而不是“圆面”。注意: 车轮为什么做成圆形?应 用 新 知骆驼祥子把车轮做成圆形,车轮上各点到车轮中心(圆心)
的距离都等于车轮的半径,
当车轮在平面上滚动时,
车轮中心与平面的距离
保持不变。因此,
当车辆在平坦的路上行使时,
坐车的人会感觉到非常平稳,
这也是车轮都做成圆形的
数学道理。结论:思考:你能说出为什么车轮不弄成正方形?点和圆的位置关系 爱好运动的小华、小强、小兵三人相邀搞一次掷飞镖比赛。他们把靶子钉在一面土墙上,规则是谁掷出落点离红心越近,谁就胜。如下图中A、B、C三点分别是他们三人某一轮掷镖的落点,你认为这一轮中谁的成绩好? ABC 如图,设⊙O 的半径为r,A点在圆内,
B点在圆上,C点在圆外,那么点A在⊙O内 点B在⊙O上 点C在⊙O外 OA<r, OB=r, OC>r. 反过来也成立,如果已知点到圆心的距离和圆的半径的关系,就可以判断点和圆的位置关系。 OA<r OB=r OC>r设⊙O 的半径为r,点P到圆心的距离OP=d,则有:点P在⊙O内 点P在⊙O上 点P在⊙O外 d<r d=r d>rd圆外的点圆内的点圆上的点 平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点。 圆的内部可以看成是到圆心的距离小于半径的点的集合;圆的外部可以看成是 。到圆心的距离大于半径的点的集合思考:平面上的一个圆把平面上的点分成哪几部分?练一练 1、⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 。 2、⊙O的半径6cm,当OP=6时,点P在 ;当OP 时点P在圆内;当OP 时,点P不在圆外。圆内圆上圆外圆上<6≤6 这节课你学到了哪些知识?有什么感想?课堂小结:定义一: 在同一平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫圆。固定的端点O叫做圆心,线段OA叫做半径。1、从运动和集合的观点理解圆的定义:定义二:圆是到定点的距离等于定长的点的集合。3、证明几个点在同一个圆上的方法。 要证明几个点在同一个圆上,只要证明这几个点与一个定点的距离相等。2、点与圆的位置关系:设⊙O的半径为r,则点P与⊙O的位置关系有:(1)点P在⊙O上 OP=r(2)点P在⊙O内 OP<r(3)点P在⊙O外 OP>r作业:再 见课后练习1,2,3
同课章节目录
