2022-2023学年苏科版九年级数学下册5.2 二次函数的图像和性质(第1课时)课件(共39张PPT)
文档属性
| 名称 | 2022-2023学年苏科版九年级数学下册5.2 二次函数的图像和性质(第1课时)课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 28.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 00:00:00 | ||
图片预览




文档简介
(共39张PPT)
二次函数的图像和性质(上)
Graphs and properties of quadratic functions
苏科版九年级下册第5章二次函数
教学目标
01
能用描点法作出函数y=ax2的图像,并能正确说出函数图像的开口方向、对称轴、顶点坐标、最值、增减性,理解a对二次函数图像的影响
02
能用描点法作出函数y=ax2+k的图像,并能理解函数y=ax2与y=ax2+k的关系,理解k对二次函数图像的影响
二次函数的图像
和性质
知识精讲
类比引入
01
我们已经学习了一次函数和反比例函数,并借助图像研究这些函数的性质;同样地,我们也可以借助图像研究二次函数的性质~
二次函数的图像究竟是什么形状呢?我们先来完成以下几个小任务~
Q1:根据二次函数表达式以y=x2,你能描述它的图像有什么特征吗?
x=0时,y=0
图像过原点
x可取一切实数,图像向左、右无限延伸
知识精讲
类比引入
01
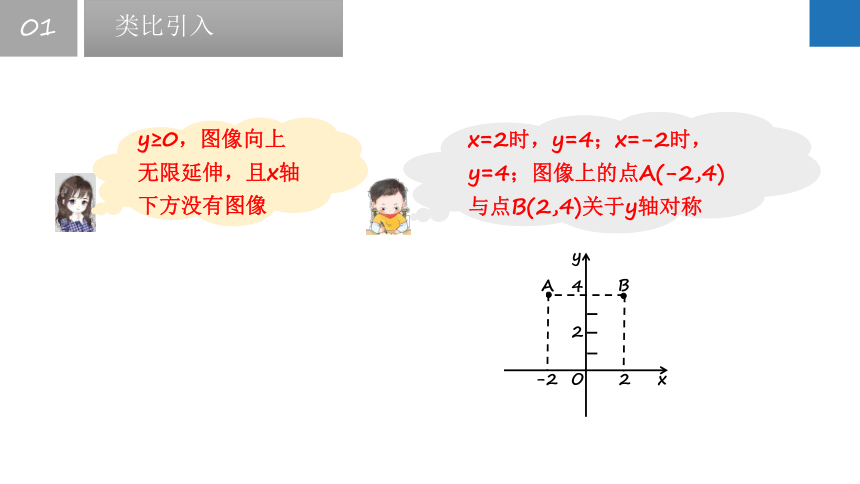
y≥0,图像向上无限延伸,且x轴下方没有图像
x=2时,y=4;x=-2时,y=4;图像上的点A(-2,4)与点B(2,4)关于y轴对称
O
-2
2
x
y
A
B
4
2
知识精讲
类比引入
01
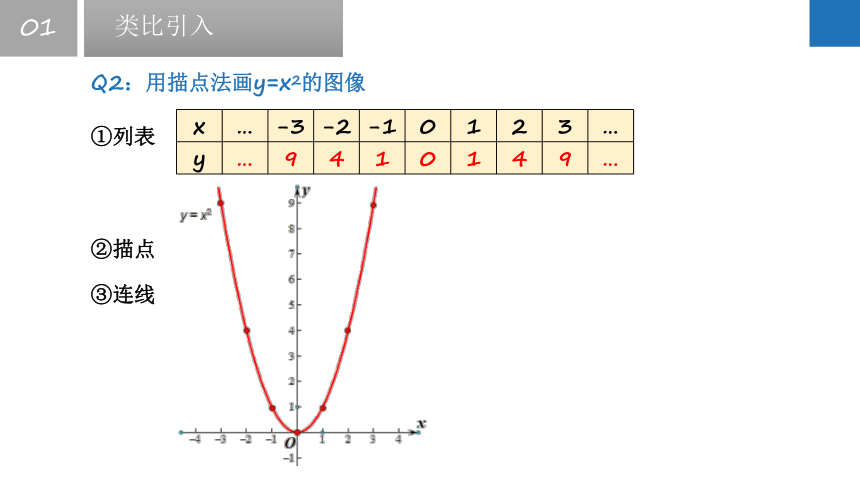
Q2:用描点法画y=x2的图像
x … -3 -2 -1 0 1 2 3 …
y … 9 4 1 0 1 4 9 …
①列表
②描点
③连线
知识精讲
类似引入
01
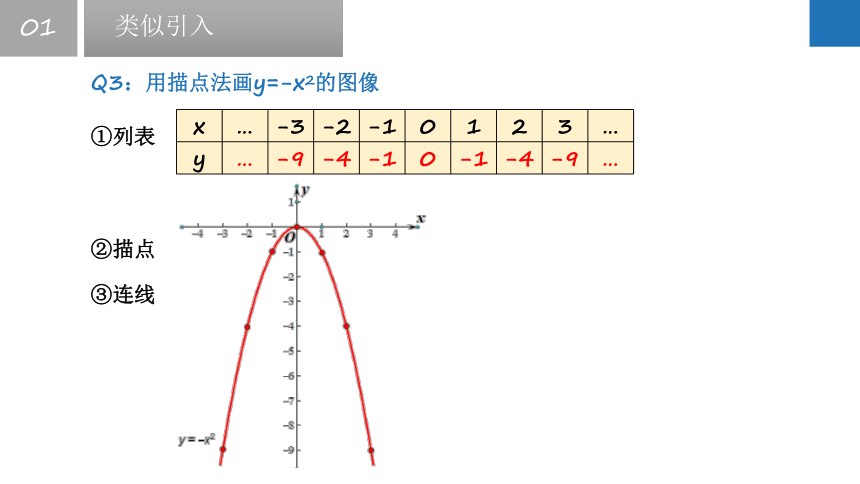
Q3:用描点法画y=-x2的图像
x … -3 -2 -1 0 1 2 3 …
y … -9 -4 -1 0 -1 -4 -9 …
①列表
②描点
③连线
知识精讲
知识精讲
02
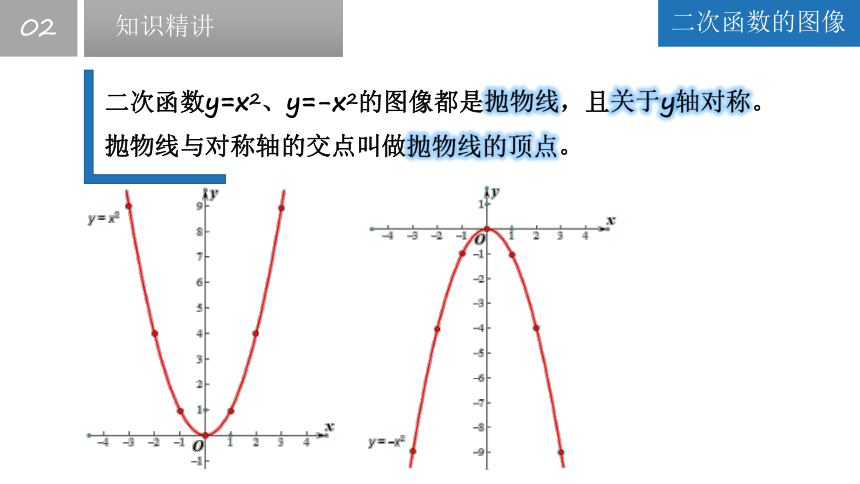
二次函数y=x2、y=-x2的图像都是抛物线,且关于y轴对称。抛物线与对称轴的交点叫做抛物线的顶点。
二次函数的图像
知识精讲
知识精讲
02
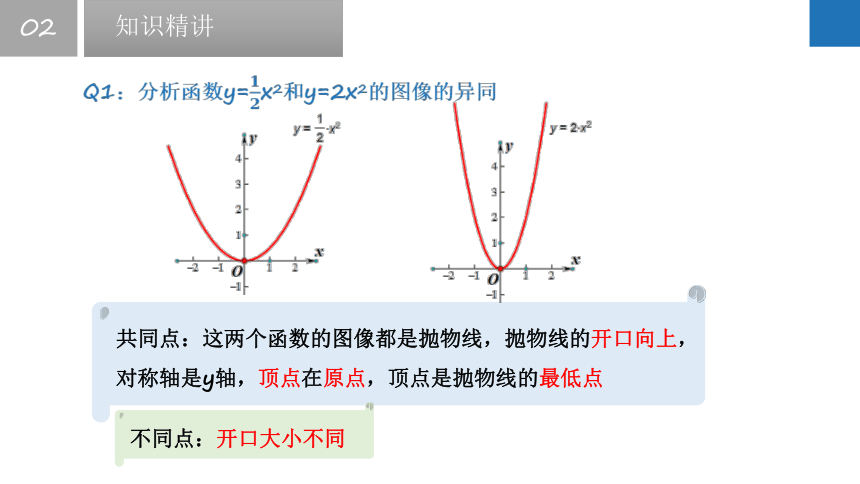
Q1:分析函数y=x2和y=2x2的图像的异同
共同点:这两个函数的图像都是抛物线,抛物线的开口向上,对称轴是y轴,顶点在原点,顶点是抛物线的最低点
不同点:开口大小不同
知识精讲
知识精讲
02
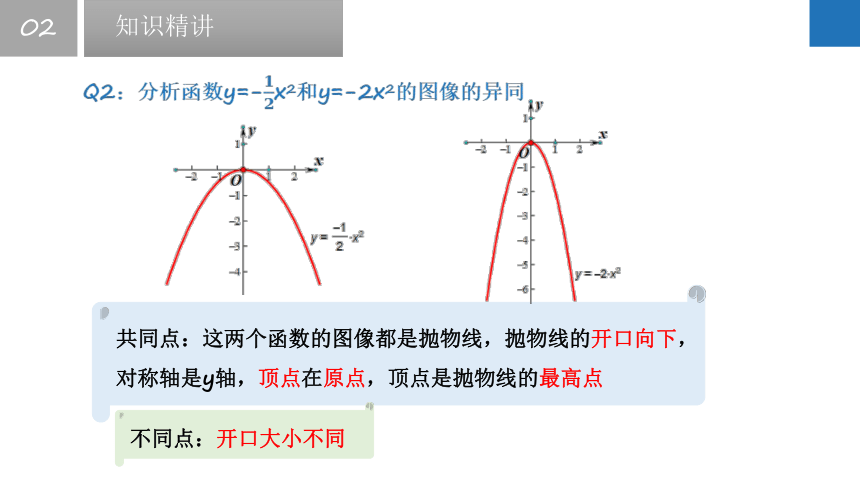
Q2:分析函数y=-x2和y=-2x2的图像的异同
共同点:这两个函数的图像都是抛物线,抛物线的开口向下,对称轴是y轴,顶点在原点,顶点是抛物线的最高点
不同点:开口大小不同
知识精讲
知识精讲
02
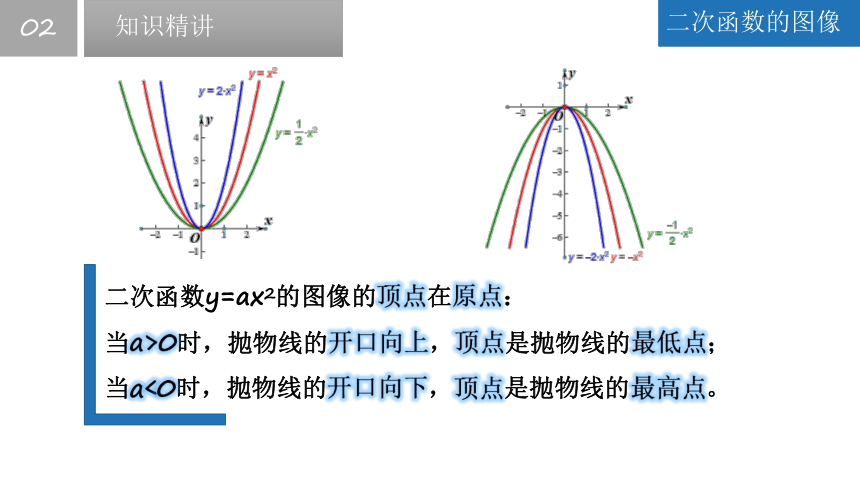
二次函数y=ax2的图像的顶点在原点:
当a>0时,抛物线的开口向上,顶点是抛物线的最低点;
当a<0时,抛物线的开口向下,顶点是抛物线的最高点。
二次函数的图像
知识精讲
知识精讲
02
二次函数的图像
当a>0时,a越大,开口越小,反之越大;
当a<0时,a越大,开口越大,反之越小。
【总结】|a|越大,开口越小
知识精讲
知识精讲
02
Q3:观察函数y=ax2的图像,你还发现了什么?
a>0时,
y轴左边的图像下降,
y轴右边的图像上升
a<0时,
y轴左边的图像上升,
y轴右边的图像下降
知识精讲
知识精讲
02
Q4:如何用x、y的值的变化来描述图像的上升、下降?
图像“上升”可以用“x增大时,y也增大”来描述
图像“下降”可以用“x增大时,y减小”来描述
二次函数y=ax2的性质:
(1)a>0
当x<0时,y随x增大而减小
当x>0时,y随x增大而增大
当x=0时,y取最小值0
(2)a<0
当x<0时,y随x增大而增大
当x>0时,y随x增大而减小
当x=0时,y取最大值是0
二次函数的性质
y=ax2(a≠0)的图像和性质举例
向上
y轴
(0,0)
最小值0
先减后增
向下
y轴
(0,0)
最大值0
先增后减
向上
y轴
(0,0)
最小值0
先减后增
向上
y轴
(0,0)
最小值0
先减后增
向下
y轴
(0,0)
最大值0
先增后减
a的正负 图像 开口 顶点坐标 对称轴 增减性
a>0 向上 (0,0) y轴(直线x=0) 当x<0时,y随x增大而减小
当x>0时,y随x增大而增大
当x=0时,y取最小值0
a>0 向下 (0,0) y轴(直线x=0) 当x<0时,y随x增大而增大
当x>0时,y随x增大而减小
当x=0时,y取最大值0
知识精讲
知识精讲
02
二次函数的图像和性质
y=ax2(a≠0)
例1-1 抛物线y=4x2中的开口方向是_______,顶点坐标是_______,对称轴是_______,函数有最小值为________;
例1-2 抛物线y=-x2中的开口方向是_______,顶点坐标是_______,对称轴是_______,函数有最大值为________.
向上
(0,0)
y轴
0
向下
(0,0)
y轴
0
例2 抛物线y=x2,y=x2,y=-x2的共同性质是:
①都是开口向上;
②都以点(0,0)为顶点;
③都以y轴为对称轴;
④都关于x轴对称;
其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
y=-x2开口向下
都关于y轴对称
B
图像平移问题(上)
知识精讲
02
Q1:用描点法画出y=x2+1的图像,并与y=x2作对比
x … -3 -2 -1 0 1 2 3 …
y=x2 … 9 4 1 0 1 4 9 …
y=x2+1 … 10 5 2 1 2 5 10 …
对于同一个自变量的值,两个函数的值相差1
将点(1,1)向上平移1个单位长度得(1,2)……
知识精讲
知识精讲
02
知识精讲
知识精讲
02
知识精讲
函数y=x2+1的图像可以由函数y=x2的图像向上平移一个单位得到
开口
顶点坐标:
对称轴:
开口向上
顶点坐标:(0,1)
对称轴:y轴
当x<0时,y随x增大而
当x>0时,y随x增大而
当x=0时,y取最小值:
当x<0时,y随x增大而减小
当x>0时,y随x增大而增大
当x=0时,y取最小值:1
知识精讲
02
Q2:用描点法画出y=x2-1的图像,并与y=x2作对比
知识精讲
x … -3 -2 -1 0 1 2 3 …
y=x2 … 9 4 1 0 1 4 9 …
y=x2-1 … 8 3 0 -1 0 3 8 …
对于同一个自变量的值,两个函数的值相差1
将点(1,1)向下平移1个单位长度得(1,0)……
知识精讲
02
知识精讲
知识精讲
02
知识精讲
函数y=x2-1的图像可以由函数y=x2的图像向下平移一个单位得到
开口
顶点坐标:
对称轴:
开口向上
顶点坐标:(0,-1)
对称轴:y轴
当x<0时,y随x增大而
当x>0时,y随x增大而
当x=0时,y取最小值:
当x<0时,y随x增大而减小
当x>0时,y随x增大而增大
当x=0时,y取最小值:-1
知识精讲
02
Q3:用描点法画出y=-x2+1的图像,并与y=-x2作对比
知识精讲
x … -3 -2 -1 0 1 2 3 …
y=-x2 … -9 -4 -1 0 -1 -4 -9 …
y=-x2+1 … -8 -3 0 1 0 -3 -8 …
知识精讲
02
知识精讲
函数y=-x2+1的图像可以由函数y=-x2的图像向上平移一个单位得到
开口
顶点坐标:
对称轴:
开口向下
顶点坐标:(0,1)
对称轴:y轴
当x<0时,y随x增大而
当x>0时,y随x增大而
当x=0时,y取最大值:
当x<0时,y随x增大而增大
当x>0时,y随x增大而减小
当x=0时,y取最大值:1
知识精讲
02
Q4:用描点法画出y=-x2-1的图像,并与y=-x2作对比
知识精讲
x … -3 -2 -1 0 1 2 3 …
y=-x2 … -9 -4 -1 0 -1 -4 -9 …
y=-x2-1 … -10 -5 -2 -1 -2 -5 -10 …
知识精讲
02
知识精讲
函数y=-x2-1的图像可以由函数y=-x2的图像向下平移一个单位得到
开口
顶点坐标:
对称轴:
开口向下
顶点坐标:(0,-1)
对称轴:y轴
当x<0时,y随x增大而
当x>0时,y随x增大而
当x=0时,y取最大值:
当x<0时,y随x增大而增大
当x>0时,y随x增大而减小
当x=0时,y取最大值:-1
知识精讲
知识精讲
02
函数y=x2+1的图像可以由函数y=x2的图像向上平移一个单位得到
函数y=x2-1的图像可以由函数y=x2的图像向下平移一个单位得到
函数y=-x2+1的图像可以由函数y=-x2的图像向上平移一个单位得到
函数y=-x2-1的图像可以由函数y=-x2的图像向下平移一个单位得到
【平移口诀】上加下减
平移口诀
向_____平移_____个单位得到
向_____平移_____个单位得到
向_____平移_____个单位得到
向_____平移_____个单位得到
y=ax2+k(a≠0)的图像和性质举例
下
4
上
8
下
3
上
6
解析式 开口方向 对称轴 顶点坐标 最值 增减性
向上
y轴
(0,-4)
最小值-4
先减后增
向下
y轴
(0,8)
最大值8
先增后减
向下
y轴
(0,-3)
最大值-3
先增后减
向上
y轴
(0,6)
最小值6
先减后增
y=ax2+k(a≠0)的图像和性质举例
知识精讲
a的正负 图像 开口 顶点坐标 对称轴 增减性
a>0 向上 (0,k) y轴(直线x=0) 当x<0时,y随x增大而减小
当x>0时,y随x增大而增大
当x=0时,y取最小值k
a>0 向下 (0,k) y轴(直线x=0) 当x<0时,y随x增大而增大
当x>0时,y随x增大而减小
当x=0时,y取最大值k
知识精讲
知识精讲
02
二次函数的图像和性质
y=ax2+k(a≠0)
例3-1 抛物线y=-x2-3是由抛物线y=-x2向_______平移_______个单位后得到;
例3-2 抛物线y=-x2+7向_______平移_______个单位后得到抛物线y=-x2-3.
下
3
10
下
例4 抛物线y=-2x2-5的开口方向_______,对称轴是_______,顶点坐标_______,是由抛物线y=-2x2向_______平移_______个单位后得到,将y=-2x2-5图像向上平移8个单位得到的抛物线解析式为_____________.
下
y轴
(0,-5)
下
5
y=-2x2+3
a的正负 图像 开口 顶点坐标 对称轴 增减性
a>0 向上 (0,0) y轴(直线x=0) 当x<0时,y随x增大而减小
当x>0时,y随x增大而增大
当x=0时,y取最小值0
a>0 向下 (0,0) y轴(直线x=0) 当x<0时,y随x增大而增大
当x>0时,y随x增大而减小
当x=0时,y取最大值0
y=ax2(a≠0)
当a>0时,a越大,开口越小,反之越大;
当a<0时,a越大,开口越大,反之越小。
【总结】|a|越大,开口越小
课后总结
课后总结
y=ax2+k(a≠0)
a的正负 图像 开口 顶点坐标 对称轴 增减性
a>0 向上 (0,k) y轴(直线x=0) 当x<0时,y随x增大而减小
当x>0时,y随x增大而增大
当x=0时,y取最小值k
a>0 向下 (0,k) y轴(直线x=0) 当x<0时,y随x增大而增大
当x>0时,y随x增大而减小
当x=0时,y取最大值k
【平移口诀】上加下减
课后预习
y=ax2(a≠0)的图像上下移动可以变为y=ax2+k(a≠0),
那左右移动又会如何呢?同学们可以先相互讨论起来哟~
谢谢学习
Thank you for learning
二次函数的图像和性质(上)
Graphs and properties of quadratic functions
苏科版九年级下册第5章二次函数
教学目标
01
能用描点法作出函数y=ax2的图像,并能正确说出函数图像的开口方向、对称轴、顶点坐标、最值、增减性,理解a对二次函数图像的影响
02
能用描点法作出函数y=ax2+k的图像,并能理解函数y=ax2与y=ax2+k的关系,理解k对二次函数图像的影响
二次函数的图像
和性质
知识精讲
类比引入
01
我们已经学习了一次函数和反比例函数,并借助图像研究这些函数的性质;同样地,我们也可以借助图像研究二次函数的性质~
二次函数的图像究竟是什么形状呢?我们先来完成以下几个小任务~
Q1:根据二次函数表达式以y=x2,你能描述它的图像有什么特征吗?
x=0时,y=0
图像过原点
x可取一切实数,图像向左、右无限延伸
知识精讲
类比引入
01
y≥0,图像向上无限延伸,且x轴下方没有图像
x=2时,y=4;x=-2时,y=4;图像上的点A(-2,4)与点B(2,4)关于y轴对称
O
-2
2
x
y
A
B
4
2
知识精讲
类比引入
01
Q2:用描点法画y=x2的图像
x … -3 -2 -1 0 1 2 3 …
y … 9 4 1 0 1 4 9 …
①列表
②描点
③连线
知识精讲
类似引入
01
Q3:用描点法画y=-x2的图像
x … -3 -2 -1 0 1 2 3 …
y … -9 -4 -1 0 -1 -4 -9 …
①列表
②描点
③连线
知识精讲
知识精讲
02
二次函数y=x2、y=-x2的图像都是抛物线,且关于y轴对称。抛物线与对称轴的交点叫做抛物线的顶点。
二次函数的图像
知识精讲
知识精讲
02
Q1:分析函数y=x2和y=2x2的图像的异同
共同点:这两个函数的图像都是抛物线,抛物线的开口向上,对称轴是y轴,顶点在原点,顶点是抛物线的最低点
不同点:开口大小不同
知识精讲
知识精讲
02
Q2:分析函数y=-x2和y=-2x2的图像的异同
共同点:这两个函数的图像都是抛物线,抛物线的开口向下,对称轴是y轴,顶点在原点,顶点是抛物线的最高点
不同点:开口大小不同
知识精讲
知识精讲
02
二次函数y=ax2的图像的顶点在原点:
当a>0时,抛物线的开口向上,顶点是抛物线的最低点;
当a<0时,抛物线的开口向下,顶点是抛物线的最高点。
二次函数的图像
知识精讲
知识精讲
02
二次函数的图像
当a>0时,a越大,开口越小,反之越大;
当a<0时,a越大,开口越大,反之越小。
【总结】|a|越大,开口越小
知识精讲
知识精讲
02
Q3:观察函数y=ax2的图像,你还发现了什么?
a>0时,
y轴左边的图像下降,
y轴右边的图像上升
a<0时,
y轴左边的图像上升,
y轴右边的图像下降
知识精讲
知识精讲
02
Q4:如何用x、y的值的变化来描述图像的上升、下降?
图像“上升”可以用“x增大时,y也增大”来描述
图像“下降”可以用“x增大时,y减小”来描述
二次函数y=ax2的性质:
(1)a>0
当x<0时,y随x增大而减小
当x>0时,y随x增大而增大
当x=0时,y取最小值0
(2)a<0
当x<0时,y随x增大而增大
当x>0时,y随x增大而减小
当x=0时,y取最大值是0
二次函数的性质
y=ax2(a≠0)的图像和性质举例
向上
y轴
(0,0)
最小值0
先减后增
向下
y轴
(0,0)
最大值0
先增后减
向上
y轴
(0,0)
最小值0
先减后增
向上
y轴
(0,0)
最小值0
先减后增
向下
y轴
(0,0)
最大值0
先增后减
a的正负 图像 开口 顶点坐标 对称轴 增减性
a>0 向上 (0,0) y轴(直线x=0) 当x<0时,y随x增大而减小
当x>0时,y随x增大而增大
当x=0时,y取最小值0
a>0 向下 (0,0) y轴(直线x=0) 当x<0时,y随x增大而增大
当x>0时,y随x增大而减小
当x=0时,y取最大值0
知识精讲
知识精讲
02
二次函数的图像和性质
y=ax2(a≠0)
例1-1 抛物线y=4x2中的开口方向是_______,顶点坐标是_______,对称轴是_______,函数有最小值为________;
例1-2 抛物线y=-x2中的开口方向是_______,顶点坐标是_______,对称轴是_______,函数有最大值为________.
向上
(0,0)
y轴
0
向下
(0,0)
y轴
0
例2 抛物线y=x2,y=x2,y=-x2的共同性质是:
①都是开口向上;
②都以点(0,0)为顶点;
③都以y轴为对称轴;
④都关于x轴对称;
其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
y=-x2开口向下
都关于y轴对称
B
图像平移问题(上)
知识精讲
02
Q1:用描点法画出y=x2+1的图像,并与y=x2作对比
x … -3 -2 -1 0 1 2 3 …
y=x2 … 9 4 1 0 1 4 9 …
y=x2+1 … 10 5 2 1 2 5 10 …
对于同一个自变量的值,两个函数的值相差1
将点(1,1)向上平移1个单位长度得(1,2)……
知识精讲
知识精讲
02
知识精讲
知识精讲
02
知识精讲
函数y=x2+1的图像可以由函数y=x2的图像向上平移一个单位得到
开口
顶点坐标:
对称轴:
开口向上
顶点坐标:(0,1)
对称轴:y轴
当x<0时,y随x增大而
当x>0时,y随x增大而
当x=0时,y取最小值:
当x<0时,y随x增大而减小
当x>0时,y随x增大而增大
当x=0时,y取最小值:1
知识精讲
02
Q2:用描点法画出y=x2-1的图像,并与y=x2作对比
知识精讲
x … -3 -2 -1 0 1 2 3 …
y=x2 … 9 4 1 0 1 4 9 …
y=x2-1 … 8 3 0 -1 0 3 8 …
对于同一个自变量的值,两个函数的值相差1
将点(1,1)向下平移1个单位长度得(1,0)……
知识精讲
02
知识精讲
知识精讲
02
知识精讲
函数y=x2-1的图像可以由函数y=x2的图像向下平移一个单位得到
开口
顶点坐标:
对称轴:
开口向上
顶点坐标:(0,-1)
对称轴:y轴
当x<0时,y随x增大而
当x>0时,y随x增大而
当x=0时,y取最小值:
当x<0时,y随x增大而减小
当x>0时,y随x增大而增大
当x=0时,y取最小值:-1
知识精讲
02
Q3:用描点法画出y=-x2+1的图像,并与y=-x2作对比
知识精讲
x … -3 -2 -1 0 1 2 3 …
y=-x2 … -9 -4 -1 0 -1 -4 -9 …
y=-x2+1 … -8 -3 0 1 0 -3 -8 …
知识精讲
02
知识精讲
函数y=-x2+1的图像可以由函数y=-x2的图像向上平移一个单位得到
开口
顶点坐标:
对称轴:
开口向下
顶点坐标:(0,1)
对称轴:y轴
当x<0时,y随x增大而
当x>0时,y随x增大而
当x=0时,y取最大值:
当x<0时,y随x增大而增大
当x>0时,y随x增大而减小
当x=0时,y取最大值:1
知识精讲
02
Q4:用描点法画出y=-x2-1的图像,并与y=-x2作对比
知识精讲
x … -3 -2 -1 0 1 2 3 …
y=-x2 … -9 -4 -1 0 -1 -4 -9 …
y=-x2-1 … -10 -5 -2 -1 -2 -5 -10 …
知识精讲
02
知识精讲
函数y=-x2-1的图像可以由函数y=-x2的图像向下平移一个单位得到
开口
顶点坐标:
对称轴:
开口向下
顶点坐标:(0,-1)
对称轴:y轴
当x<0时,y随x增大而
当x>0时,y随x增大而
当x=0时,y取最大值:
当x<0时,y随x增大而增大
当x>0时,y随x增大而减小
当x=0时,y取最大值:-1
知识精讲
知识精讲
02
函数y=x2+1的图像可以由函数y=x2的图像向上平移一个单位得到
函数y=x2-1的图像可以由函数y=x2的图像向下平移一个单位得到
函数y=-x2+1的图像可以由函数y=-x2的图像向上平移一个单位得到
函数y=-x2-1的图像可以由函数y=-x2的图像向下平移一个单位得到
【平移口诀】上加下减
平移口诀
向_____平移_____个单位得到
向_____平移_____个单位得到
向_____平移_____个单位得到
向_____平移_____个单位得到
y=ax2+k(a≠0)的图像和性质举例
下
4
上
8
下
3
上
6
解析式 开口方向 对称轴 顶点坐标 最值 增减性
向上
y轴
(0,-4)
最小值-4
先减后增
向下
y轴
(0,8)
最大值8
先增后减
向下
y轴
(0,-3)
最大值-3
先增后减
向上
y轴
(0,6)
最小值6
先减后增
y=ax2+k(a≠0)的图像和性质举例
知识精讲
a的正负 图像 开口 顶点坐标 对称轴 增减性
a>0 向上 (0,k) y轴(直线x=0) 当x<0时,y随x增大而减小
当x>0时,y随x增大而增大
当x=0时,y取最小值k
a>0 向下 (0,k) y轴(直线x=0) 当x<0时,y随x增大而增大
当x>0时,y随x增大而减小
当x=0时,y取最大值k
知识精讲
知识精讲
02
二次函数的图像和性质
y=ax2+k(a≠0)
例3-1 抛物线y=-x2-3是由抛物线y=-x2向_______平移_______个单位后得到;
例3-2 抛物线y=-x2+7向_______平移_______个单位后得到抛物线y=-x2-3.
下
3
10
下
例4 抛物线y=-2x2-5的开口方向_______,对称轴是_______,顶点坐标_______,是由抛物线y=-2x2向_______平移_______个单位后得到,将y=-2x2-5图像向上平移8个单位得到的抛物线解析式为_____________.
下
y轴
(0,-5)
下
5
y=-2x2+3
a的正负 图像 开口 顶点坐标 对称轴 增减性
a>0 向上 (0,0) y轴(直线x=0) 当x<0时,y随x增大而减小
当x>0时,y随x增大而增大
当x=0时,y取最小值0
a>0 向下 (0,0) y轴(直线x=0) 当x<0时,y随x增大而增大
当x>0时,y随x增大而减小
当x=0时,y取最大值0
y=ax2(a≠0)
当a>0时,a越大,开口越小,反之越大;
当a<0时,a越大,开口越大,反之越小。
【总结】|a|越大,开口越小
课后总结
课后总结
y=ax2+k(a≠0)
a的正负 图像 开口 顶点坐标 对称轴 增减性
a>0 向上 (0,k) y轴(直线x=0) 当x<0时,y随x增大而减小
当x>0时,y随x增大而增大
当x=0时,y取最小值k
a>0 向下 (0,k) y轴(直线x=0) 当x<0时,y随x增大而增大
当x>0时,y随x增大而减小
当x=0时,y取最大值k
【平移口诀】上加下减
课后预习
y=ax2(a≠0)的图像上下移动可以变为y=ax2+k(a≠0),
那左右移动又会如何呢?同学们可以先相互讨论起来哟~
谢谢学习
Thank you for learning
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
