2022-2023学年人教版八年级数学上学期13.2 画轴对称图形(2课时)(共23张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上学期13.2 画轴对称图形(2课时)(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 698.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
13.2 画轴对称图形
画轴对称图形
01
知识回顾
1. 轴对称图形
2. 轴对称图形的性质
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形。
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
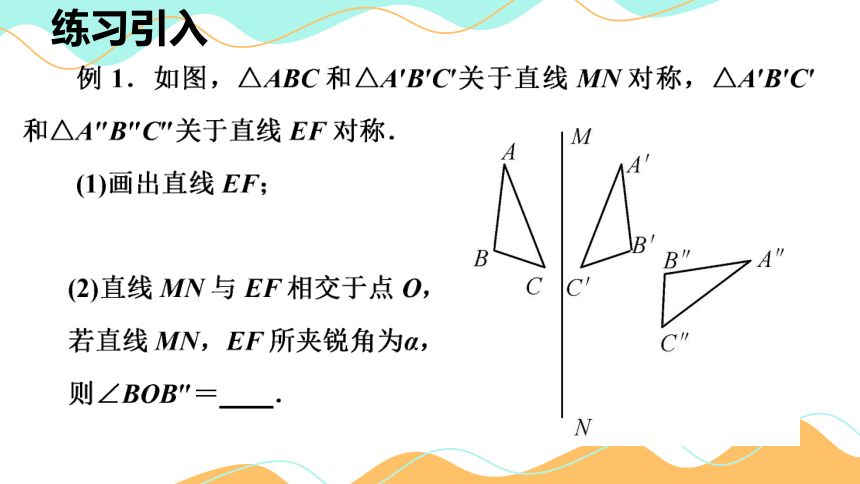
练习引入
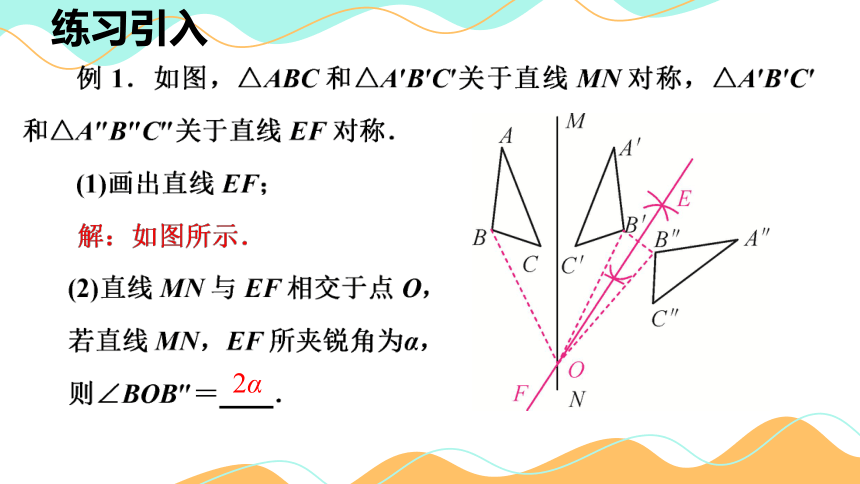
练习引入
2α
小结:如果两个图形成轴对称,其对称轴是任何一组对应点所连线段的垂直平分线.因此,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
思考:
如果我们已知一条直线和一个图形,能不能画出这个图形关于这这条直线对称的图形呢?
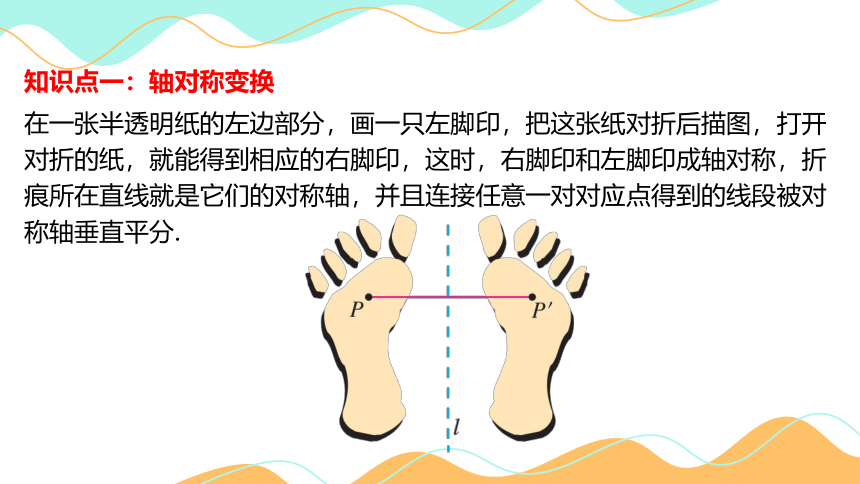
知识点一:轴对称变换
在一张半透明纸的左边部分,画一只左脚印,把这张纸对折后描图,打开对折的纸,就能得到相应的右脚印,这时,右脚印和左脚印成轴对称,折痕所在直线就是它们的对称轴,并且连接任意一对对应点得到的线段被对称轴垂直平分.
由一个平面图形可以得到与它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全相同;新图形上的每一点都是原图形上的某一点关于直线l的对称点;连接任意一对对应点的线段被对称轴垂直平分.
知识点一:轴对称变换
知识点二:作轴对称图形
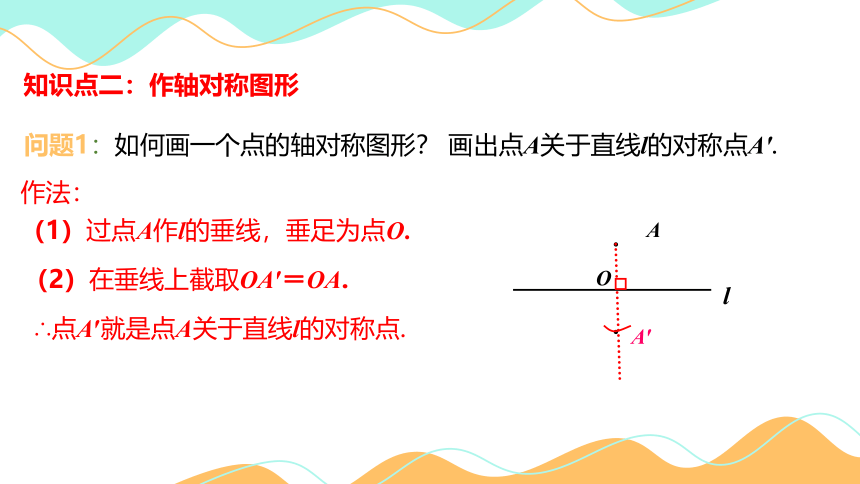
问题1:如何画一个点的轴对称图形? 画出点A关于直线l的对称点A′.
﹒
l
A
﹒
A′
O
作法:
(1)过点A作l的垂线,垂足为点O.
(2)在垂线上截取OA′=OA.
∴点A′就是点A关于直线l的对称点.
问题2:如何画一条线段的对称图形?已知线段AB,画出AB关于直线l的对称线段
A
B
(图1)
(图2)
(图3)
A
B
l
l
A
B
l
A ′
A ′
A ′
B ′
(B ′)
B ′
问题3:如何画一个图形的对称图形?已知△ABC和直线l,画出△ABC关于直线l的对称三角形。
作法:
(1) 过点A画直线l的垂线,垂足为点O,在垂线上截取OA′=OA,A′就是点A关于直线l的对称点.
(3) 连接A′B′,B′C′,C′A′,得到△A′B′C′即为所求.
(2) 同理,分别画出点B,C关于直线l的对称点B′,C′ .
A
B
C
A′
B′
C′
O
练习1:如何画一个图形的对称图形?已知△ABC和直线l,画出△ABC关于直线l的对称三角形。
《名校》3(3)如图,画△ABC关于直线l的对称图形.
m
A
B
C
(A ′)
C ′
B ′
练习2:在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面给出的图中画出4个这样的△DEF.
A
B
C
A
B
C
A
B
C
(F)
(D)
E
(E)
F
D
(F)
D
E
(D)
(E)
F
方法归纳:作一个图形关于一条已知直线的对称图形,关键是作出图形上一些点关于这条直线的对称点,然后再根据已知图形将这些点连接起来.
作轴对称图形的方法
几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
1. 先找( ),
2. 作出其( ),
3. 顺次连结( )构成轴对称图形 .
特殊点
对称点
对称点
作轴对称图形的步骤
归纳小结
用坐标表示轴对称
02
知识点三:作轴对称图形
画出已知点及其对称点,并把坐标填入表格中
y
x
已知点
关于x轴对称点
关于y轴对称点
A(2,-3)
B(-1,2)
C(-6,-5)
D(0.5,1)
E(4,0)
A′(2,3)
A″( -2,-3 )
B″( 1,2)
B′( -1,-2)
C′( -6,5 )
C″( 6,-5)
D′(0.5,-1 )
D″(- 0.5,1 )
E′( 4,0 )
E″(- 4,0 )
B
A
C
A′
A″
B′
C′
C″
D
E′
E″
E
D′
D″
B″
你能说出这些点关于X轴,Y轴对称点的坐标关系吗?
点(x, y)关于y轴对称的点的坐标为_______.
点(x, y)关于x轴对称的点的坐标为_______.
在平面直角坐标系中,
关于x轴对称的点横坐标相等,纵坐标互为相反数.
(x, - y)
(- x, y)
关于y轴对称的点横坐标互为相反数,纵坐标相等.
归纳小结
1、点P(-5, 6)与点Q关于x轴对称,则点Q的坐标为__________.
(- 5 , -6 )
2、点M(a, -5)与点N(-2, b)关于x轴对称,则a=_____, b =_____.
-2
5
3、点P(-5, 6)与点Q关于y轴对称,则点Q的坐标为__________.
( 5 , 6 )
4、点M(a, -5)与点N(-2, b)关于y轴对称,则a=_____, b =_____.
2
-5
练习3:填空
5、已知点P(2a+b,-3a)与点P′ (8,b+2).
若点p与点p ′关于x轴对称,则a=_____ b=_______.
若点p与点p ′关于y轴对称,则a=_____ b=_______.
{
2a+b=8
3a=b+2
{
b=4
a=2
{
2a+b=-8
-3a=b+2
{
b=-20
a=6
b=-20
a=6
练习4:《名校》小专题6 网格作图
13.2 画轴对称图形
画轴对称图形
01
知识回顾
1. 轴对称图形
2. 轴对称图形的性质
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形。
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
练习引入
练习引入
2α
小结:如果两个图形成轴对称,其对称轴是任何一组对应点所连线段的垂直平分线.因此,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
思考:
如果我们已知一条直线和一个图形,能不能画出这个图形关于这这条直线对称的图形呢?
知识点一:轴对称变换
在一张半透明纸的左边部分,画一只左脚印,把这张纸对折后描图,打开对折的纸,就能得到相应的右脚印,这时,右脚印和左脚印成轴对称,折痕所在直线就是它们的对称轴,并且连接任意一对对应点得到的线段被对称轴垂直平分.
由一个平面图形可以得到与它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全相同;新图形上的每一点都是原图形上的某一点关于直线l的对称点;连接任意一对对应点的线段被对称轴垂直平分.
知识点一:轴对称变换
知识点二:作轴对称图形
问题1:如何画一个点的轴对称图形? 画出点A关于直线l的对称点A′.
﹒
l
A
﹒
A′
O
作法:
(1)过点A作l的垂线,垂足为点O.
(2)在垂线上截取OA′=OA.
∴点A′就是点A关于直线l的对称点.
问题2:如何画一条线段的对称图形?已知线段AB,画出AB关于直线l的对称线段
A
B
(图1)
(图2)
(图3)
A
B
l
l
A
B
l
A ′
A ′
A ′
B ′
(B ′)
B ′
问题3:如何画一个图形的对称图形?已知△ABC和直线l,画出△ABC关于直线l的对称三角形。
作法:
(1) 过点A画直线l的垂线,垂足为点O,在垂线上截取OA′=OA,A′就是点A关于直线l的对称点.
(3) 连接A′B′,B′C′,C′A′,得到△A′B′C′即为所求.
(2) 同理,分别画出点B,C关于直线l的对称点B′,C′ .
A
B
C
A′
B′
C′
O
练习1:如何画一个图形的对称图形?已知△ABC和直线l,画出△ABC关于直线l的对称三角形。
《名校》3(3)如图,画△ABC关于直线l的对称图形.
m
A
B
C
(A ′)
C ′
B ′
练习2:在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面给出的图中画出4个这样的△DEF.
A
B
C
A
B
C
A
B
C
(F)
(D)
E
(E)
F
D
(F)
D
E
(D)
(E)
F
方法归纳:作一个图形关于一条已知直线的对称图形,关键是作出图形上一些点关于这条直线的对称点,然后再根据已知图形将这些点连接起来.
作轴对称图形的方法
几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
1. 先找( ),
2. 作出其( ),
3. 顺次连结( )构成轴对称图形 .
特殊点
对称点
对称点
作轴对称图形的步骤
归纳小结
用坐标表示轴对称
02
知识点三:作轴对称图形
画出已知点及其对称点,并把坐标填入表格中
y
x
已知点
关于x轴对称点
关于y轴对称点
A(2,-3)
B(-1,2)
C(-6,-5)
D(0.5,1)
E(4,0)
A′(2,3)
A″( -2,-3 )
B″( 1,2)
B′( -1,-2)
C′( -6,5 )
C″( 6,-5)
D′(0.5,-1 )
D″(- 0.5,1 )
E′( 4,0 )
E″(- 4,0 )
B
A
C
A′
A″
B′
C′
C″
D
E′
E″
E
D′
D″
B″
你能说出这些点关于X轴,Y轴对称点的坐标关系吗?
点(x, y)关于y轴对称的点的坐标为_______.
点(x, y)关于x轴对称的点的坐标为_______.
在平面直角坐标系中,
关于x轴对称的点横坐标相等,纵坐标互为相反数.
(x, - y)
(- x, y)
关于y轴对称的点横坐标互为相反数,纵坐标相等.
归纳小结
1、点P(-5, 6)与点Q关于x轴对称,则点Q的坐标为__________.
(- 5 , -6 )
2、点M(a, -5)与点N(-2, b)关于x轴对称,则a=_____, b =_____.
-2
5
3、点P(-5, 6)与点Q关于y轴对称,则点Q的坐标为__________.
( 5 , 6 )
4、点M(a, -5)与点N(-2, b)关于y轴对称,则a=_____, b =_____.
2
-5
练习3:填空
5、已知点P(2a+b,-3a)与点P′ (8,b+2).
若点p与点p ′关于x轴对称,则a=_____ b=_______.
若点p与点p ′关于y轴对称,则a=_____ b=_______.
{
2a+b=8
3a=b+2
{
b=4
a=2
{
2a+b=-8
-3a=b+2
{
b=-20
a=6
b=-20
a=6
练习4:《名校》小专题6 网格作图
