河南省郑州市郑东新区外国语学校2022-2023学年八年级上学期开学考试数学试题(含解析)
文档属性
| 名称 | 河南省郑州市郑东新区外国语学校2022-2023学年八年级上学期开学考试数学试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 433.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 00:00:00 | ||
图片预览



文档简介
2022-2023学年河南省郑州市郑东新区外国语学校八年级(上)开学数学试卷(含答案与解析)
一、选择题(每小题3分,共30分)
1.(3分)下列四组数据中,不能作为直角三角形的三边长的是( )
A.3,4,6 B.7,24,25 C.6,8,10 D.9,12,15
2.(3分)在﹣,2π,,,0,中无理数个数为( )
A.1个 B.2个 C.3个 D.4个
3.(3分)分析下列说法:①实数与数轴上的点一一对应;②﹣a2没有平方根;③任何实数的立方根有且只有一个;④平方根与立方根相同的数是0和1.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.(3分)在平面直角坐标系中,点(1,﹣3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(3分)下列计算正确的是( )
A. B.
C. D.
6.(3分)如图,在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是( )
A.(2,1) B.(1,2) C.(,1) D.(1,)
7.(3分)已知m+n=2,mn=﹣2,则(1﹣m)(1﹣n)的值为( )
A.﹣3 B.﹣1 C.1 D.5
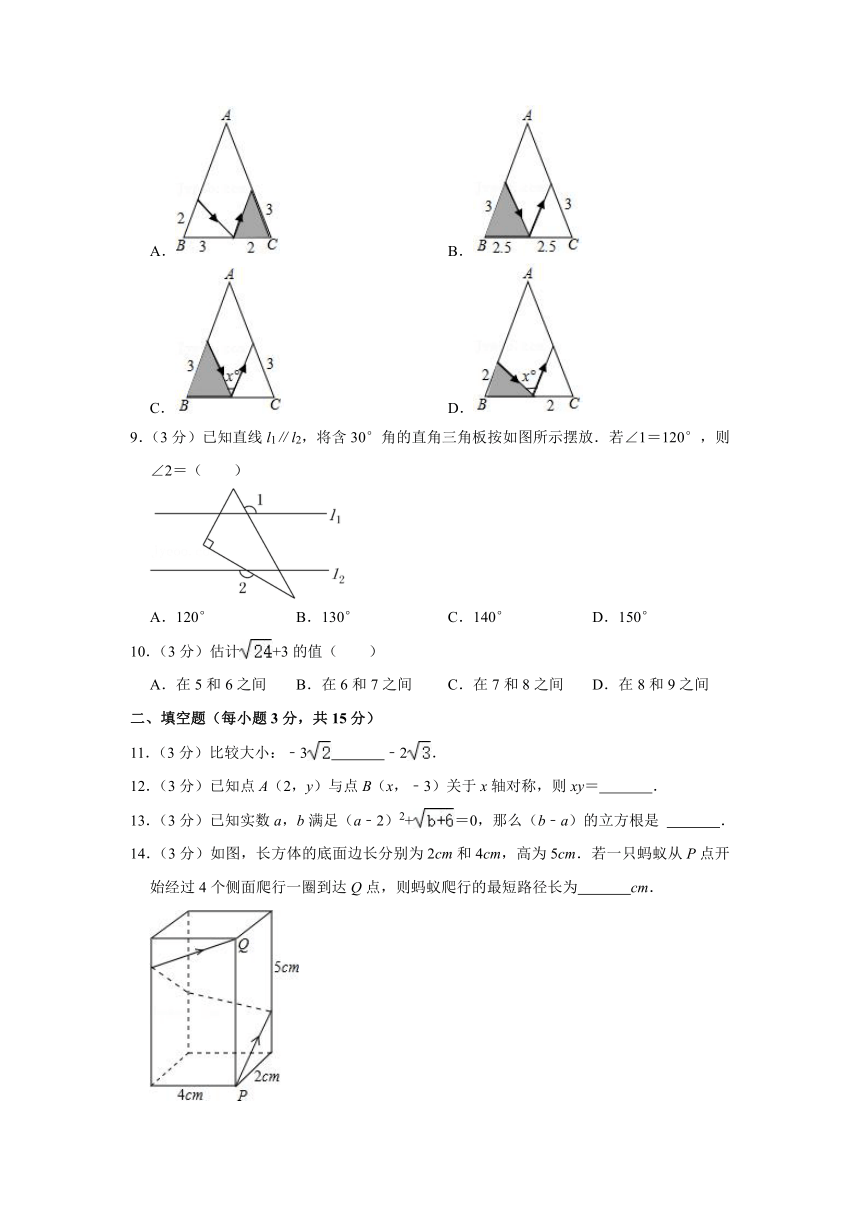
8.(3分)如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )
A. B.
C. D.
9.(3分)已知直线l1∥l2,将含30°角的直角三角板按如图所示摆放.若∠1=120°,则∠2=( )
A.120° B.130° C.140° D.150°
10.(3分)估计+3的值( )
A.在5和6之间 B.在6和7之间 C.在7和8之间 D.在8和9之间
二、填空题(每小题3分,共15分)
11.(3分)比较大小:﹣3 ﹣2.
12.(3分)已知点A(2,y)与点B(x,﹣3)关于x轴对称,则xy= .
13.(3分)已知实数a,b满足(a﹣2)2+=0,那么(b﹣a)的立方根是 .
14.(3分)如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为 cm.
15.(3分)如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿着直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为 cm.
三、计算题(每题3分,共18分)
16.(18分)(1);
(2);
(3);
(4)(1+2x)3﹣=1;
(5)2;
(6).
四、解答题(共30分)
17.(6分)已知x﹣1的平方根是±3,2x+y+7的立方根是2,求7﹣x﹣y的平方根.
18.(7分)如图,有一空心圆柱,高为12cm,底面周长为15cm,在圆柱内的下底面A处有一只蝴蝶,它想和上底面B处的同伴汇合,则这只蝴蝶经过的最短距离是多少cm?(π取3)
19.(8分)如图所示,缉毒警方在基地B处获知有贩毒分子分别在P岛和M岛进行毒品交易后,缉毒艇立即出发,已知甲艇沿北偏东60°方向以每小时36海里的速度前进,乙艇沿南偏东30°方向以每小时32海里的速度前进,半小时后甲到M岛,乙到P岛,则M岛与P岛之间的距离是多少?(结果保留根号)
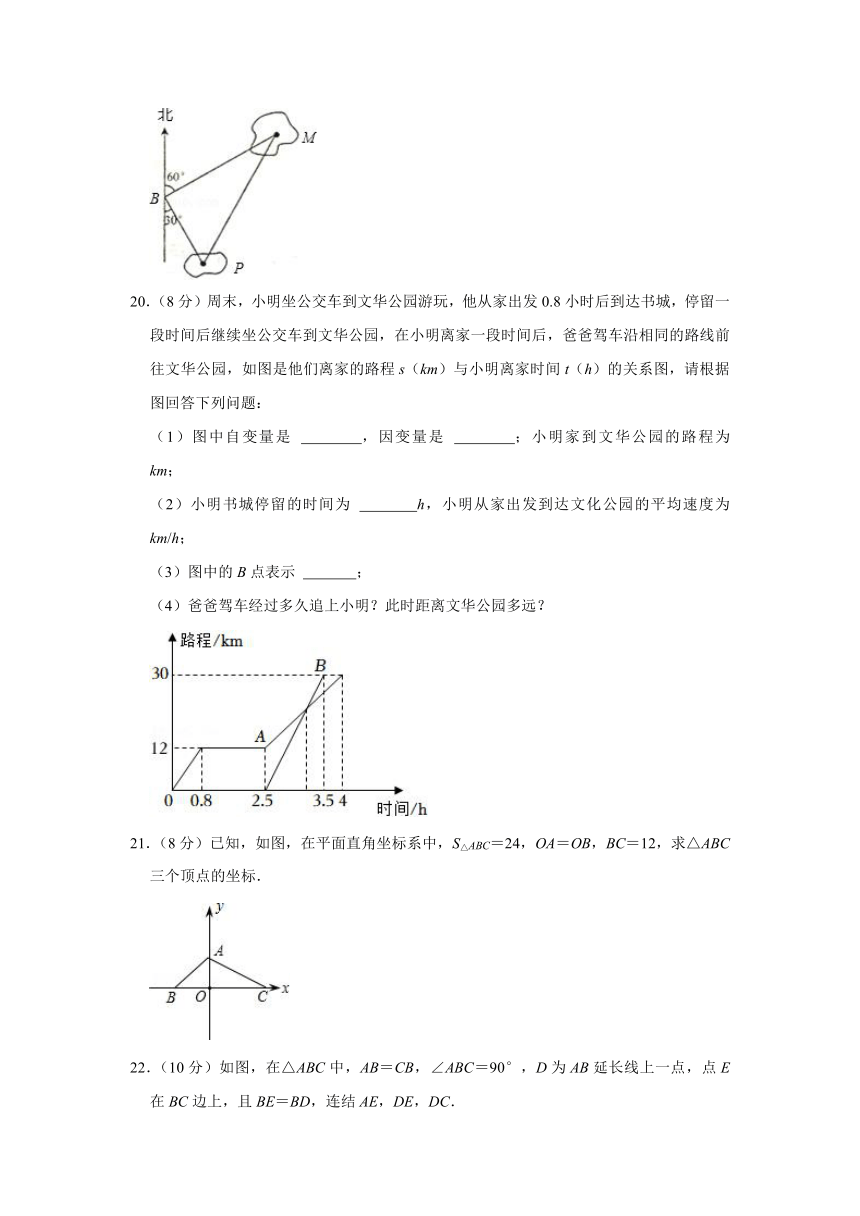
20.(8分)周末,小明坐公交车到文华公园游玩,他从家出发0.8小时后到达书城,停留一段时间后继续坐公交车到文华公园,在小明离家一段时间后,爸爸驾车沿相同的路线前往文华公园,如图是他们离家的路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是 ,因变量是 ;小明家到文华公园的路程为 km;
(2)小明书城停留的时间为 h,小明从家出发到达文化公园的平均速度为 km/h;
(3)图中的B点表示 ;
(4)爸爸驾车经过多久追上小明?此时距离文华公园多远?
21.(8分)已知,如图,在平面直角坐标系中,S△ABC=24,OA=OB,BC=12,求△ABC三个顶点的坐标.
22.(10分)如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE,DE,DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=15°,求∠BDC的度数.
23.(10分)先阅读下列的解答过程,然后再解答:
形如的化简,只要我们找到两个数a、b,使a+b=m,ab=n,使得=m,,
那么便有:(a>b)
例如:化简.
解:首先把化为,这里m=7,n=12,由于4+3=7,4×3=12即=7,;
∴.
由上述例题的方法化简:.
2022-2023学年河南省郑州市郑东新区外国语学校八年级(上)开学数学试卷
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.(3分)下列四组数据中,不能作为直角三角形的三边长的是( )
A.3,4,6 B.7,24,25 C.6,8,10 D.9,12,15
【分析】判断是否为直角三角形,只要验证两小边的平方和等于最长边的平方即可.
【解答】解:A、32+42≠62,不能组成直角三角形,符合题意;
B、72+242=252,能组成直角三角形,不符合题意;
C、62+82=102,能组成直角三角形,不符合题意;
D、92+122=152,能组成直角三角形,不符合题意.
故选:A.
【点评】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
2.(3分)在﹣,2π,,,0,中无理数个数为( )
A.1个 B.2个 C.3个 D.4个
【分析】由于开不尽方才是无理数,无限不循环小数为无理数,所以根据无理数的定义即可判定选择项.
【解答】解:在﹣,2π,,,0,中,
根据无理数的定义可得,无理数有2π,,三个.
故选:C.
【点评】此题主要考查了无理数定义.解题时注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,,0.8080080008…(每两个8之间依次多1个0)等形式.
3.(3分)分析下列说法:①实数与数轴上的点一一对应;②﹣a2没有平方根;③任何实数的立方根有且只有一个;④平方根与立方根相同的数是0和1.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】本题考查实数与数轴的点的关系及实数的有关性质,依次分析可得答案.
【解答】解:依次分析可得:
①实数与数轴上的点一一对应,符合实数与数轴上的点的关系,正确;
②a=0时,﹣a2=0,平方根为0,故错误;
③任何实数的立方根有且只有一个,正确;
④平方根与立方根相同的数是0,而1的平方根是±1,而立方根是1,不正确.
①③正确,
故选:B.
【点评】本题考查实数与数轴的点的关系及实数的有关性质.
4.(3分)在平面直角坐标系中,点(1,﹣3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据各象限内点的坐标特征解答.
【解答】解:点(1,﹣3)在第四象限.
故选:D.
【点评】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
5.(3分)下列计算正确的是( )
A. B.
C. D.
【分析】根据二次根式的混合运算法则即可直接解题.
【解答】解:A、非同类二次根式的被开方数不能直接相减,故错误.
B、∵π>3,被开方数的算术平方根为非负数,故错误.
C、=≠3,故错误.
D、==,故正确.
故选:D.
【点评】本题考查了二次根式的混合运算,难度不大,重点掌握二次根式的混合运算法则.
6.(3分)如图,在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是( )
A.(2,1) B.(1,2) C.(,1) D.(1,)
【分析】首先过点A作AC⊥OB于点C,由△AOB是等边三角形,若B点的坐标是(2,0),可求得OA=OB=2,OC=1,然后由勾股定理求得AC的长,则可求得答案.
【解答】解:过点A作AC⊥OB于点C,
∵B点的坐标是(2,0),
∴OB=2,
∵△AOB是等边三角形,
∴OA=OB=2,OC=OB=1,
在Rt△OAC中,AC==,
∴A点的坐标是:(1,).
故选:D.
【点评】此题考查了等边三角形的性质以及勾股定理.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.
7.(3分)已知m+n=2,mn=﹣2,则(1﹣m)(1﹣n)的值为( )
A.﹣3 B.﹣1 C.1 D.5
【分析】多项式乘多项式法则,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积转换成以m+n,mn为整体相加的形式,代入求值.
【解答】解:∵m+n=2,mn=﹣2,
∴(1﹣m)(1﹣n),
=1﹣(m+n)+mn,
=1﹣2﹣2,
=﹣3.
故选:A.
【点评】本题考查了多项式乘多项式法则,合并同类项时要注意项中的指数及字母是否相同.
8.(3分)如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )
A. B.
C. D.
【分析】根据全等三角形的判定定理进行判断.
【解答】解:A、由全等三角形的判定定理SAS证得图中两个小三角形全等,
故本选项不符合题意;
B、由全等三角形的判定定理SAS证得图中两个小三角形全等,
故本选项不符合题意;
C、如图1,∵∠DEC=∠B+∠BDE,
∴x°+∠FEC=x°+∠BDE,
∴∠FEC=∠BDE,
所以其对应边应该是BE和CF,而已知给的是BD=FC=3,
所以不能判定两个小三角形全等,故本选项符合题意;
D、如图2,∵∠DEC=∠B+∠BDE,
∴x°+∠FEC=x°+∠BDE,
∴∠FEC=∠BDE,
∵BD=EC=2,∠B=∠C,
∴△BDE≌△CEF,
所以能判定两个小三角形全等,故本选项不符合题意;
由于本题选择可能得不到全等三角形纸片的图形,
故选:C.
【点评】本题考查了全等三角形的判定,注意三角形边和角的对应关系是关键.
9.(3分)已知直线l1∥l2,将含30°角的直角三角板按如图所示摆放.若∠1=120°,则∠2=( )
A.120° B.130° C.140° D.150°
【分析】过点B作BF∥l1,交AC于点F,利用三角形的外角的性质,平行线的性质定理和对顶角相等的性质解答即可.
【解答】解:过含30°角的直角三角板的直角顶点B作BF∥l1,交AC于点F,
∵∠C=30°,
∴∠A=90°﹣∠C=60°.
∵∠1=∠A+∠ADE,
∴∠ADE=60°.
∵BF∥l1,
∴∠ABF=∠ADE=60°,
∴∠FBG=90°﹣∠ABF=30°.
∵BF∥l1,l1∥l2,
∴BF∥l2,
∴∠BGH+∠FBG=180°,
∴∠BGH=180°﹣∠FBG=150°,
∴∠2=∠BGH=150°.
故选:D.
【点评】本题主要考查了直角三角形的两个锐角互余,平行线的性质定理,三角形的外角的性质,对顶角相等,过点B作BF∥l1,交AC于点F是解题的关键.
10.(3分)估计+3的值( )
A.在5和6之间 B.在6和7之间 C.在7和8之间 D.在8和9之间
【分析】先估计的整数部分,然后即可判断+3的近似值.
【解答】解:∵42=16,52=25,
所以,
所以+3在7到8之间.
故选:C.
【点评】此题主要考查了估算无理数的大小的能力,理解无理数性质,估算其数值.现实生活中经常需要估算,估算应是我们具备的数学能力,“夹逼法”是估算的一般方法,也是常用方法.
二、填空题(每小题3分,共15分)
11.(3分)比较大小:﹣3 < ﹣2.
【分析】先把两数平方,再根据实数比较大小的方法即可比较大小.
【解答】解:∵(3)2=18,(2)2=12,
∴﹣3<﹣2.
故答案为:<.
【点评】此题主要考查了实数的大小的比较,实数大小比较法则:
(1)正数大于0,0大于负数,正数大于负数;
(2)两个负数,绝对值大的反而小.
12.(3分)已知点A(2,y)与点B(x,﹣3)关于x轴对称,则xy= 6 .
【分析】根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变,可得到x、y的值,进而计算出答案.
【解答】解:∵点A(2,y)与点B(x,﹣3)关于y轴对称,
∴x=﹣2,y=﹣3,
∴xy=6,
故答案为:6.
【点评】此题主要考查了关于y轴对称点的坐标特点,关键是掌握点的变化规律.
13.(3分)已知实数a,b满足(a﹣2)2+=0,那么(b﹣a)的立方根是 ﹣2 .
【分析】根据非负数的性质即可求出a与b的值,然后代入b﹣a即可求出答案.
【解答】解:由题意可知:a﹣2=0,b+6=0,
∴a=2,b=﹣6,
∴b﹣a=﹣6﹣2=﹣8,
∴﹣8的立方根是﹣2.
故答案为:﹣2.
【点评】本题考查立方根的定义,解题的关键是熟练运用立方根的定义,本题属于基础题型.
14.(3分)如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为 13 cm.
【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将长方体展开,然后利用两点之间线段最短解答.
【解答】解:
∵PA=2×(4+2)=12,QA=5
∴PQ=13.
故答案为:13.
【点评】本题主要考查两点之间线段最短,以及如何把立体图形转化成平面图形.
15.(3分)如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿着直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为 3 cm.
【分析】由折叠的性质知CD=DE,AC=AE.根据题意在Rt△BDE中运用勾股定理求DE.
【解答】解:由勾股定理得,AB=10.
由折叠的性质知,AE=AC=6,DE=CD,∠AED=∠C=90°.
∴BE=AB﹣AE=10﹣6=4,
在Rt△BDE中,由勾股定理得,
DE2+BE2=BD2
即CD2+42=(8﹣CD)2,
解得:CD=3cm.
【点评】本题利用了:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、勾股定理求解.
三、计算题(每题3分,共18分)
16.(18分)(1);
(2);
(3);
(4)(1+2x)3﹣=1;
(5)2;
(6).
【分析】(1)根据完全平方公式计算即可求解;
(2)根据二次根式乘除法运算的计算法则计算即可求解;
(3)先算小括号里面的减法,再算括号外面的乘法;
(4)先移项,再合并同类项,再开立方即可求解;
(5)先化简,再计算加法;
(6)先化简,再计算加减法.
【解答】解:(1)
=1﹣4+8
=9﹣4;
(2)
=
=;
(3)
=(3﹣4)×
=﹣×
=﹣3;
(4)(1+2x)3﹣=1,
(1+2x)3=+1,
(1+2x)3=,
1+2x=,
2x=﹣1,
2x=,
x=;
(5)2
=4+12
=16;
(6)
=5+﹣18﹣
=﹣13.
【点评】本题考查了二次根式的混合运算,在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.同时考查了立方根.
四、解答题(共30分)
17.(6分)已知x﹣1的平方根是±3,2x+y+7的立方根是2,求7﹣x﹣y的平方根.
【分析】根据题意分别确定x﹣1及2x+y+7的值,继而化简后可得出答案.
【解答】解:由题意得:x﹣1=9①,2x+y+7=8②,
②﹣①得:x+y+8=﹣1,
∴x+y=﹣9,
∴7﹣x﹣y=7﹣(x+y)=16,
它的平方根为±4.
【点评】本题考查了平方根及立方根的知识,比较简单,注意一个正数的平方根有两个.
18.(7分)如图,有一空心圆柱,高为12cm,底面周长为15cm,在圆柱内的下底面A处有一只蝴蝶,它想和上底面B处的同伴汇合,则这只蝴蝶经过的最短距离是多少cm?(π取3)
【分析】先把圆柱的侧面展开得其侧面展开图,则A,B所在的长方形的长为圆柱的高12cm,宽为底面圆周长的一半为πr,蝴蝶经过的最短距离为连接A,B的线段长,由勾股定理求得AB的长.
【解答】解:如图,将圆柱的侧面沿过A点的一条母线剪开,得到长方形ADFE,
连接AB,则线段AB的长就是蝴蝶爬行的最短距离,其中C,B分别是AE,DF的中点.
∵AD=12cm,DB=πr=7.5cm,
∴AB故蝴蝶经过的最短距离为:(cm).
答:这只蝴蝶经过的最短距离是cm.
【点评】此题考查平面展开﹣最短路径问题,关键是根据勾股定理解答.
19.(8分)如图所示,缉毒警方在基地B处获知有贩毒分子分别在P岛和M岛进行毒品交易后,缉毒艇立即出发,已知甲艇沿北偏东60°方向以每小时36海里的速度前进,乙艇沿南偏东30°方向以每小时32海里的速度前进,半小时后甲到M岛,乙到P岛,则M岛与P岛之间的距离是多少?(结果保留根号)
【分析】根据条件可以证得△BMN是直角三角形,求得BP与BM的长,根据勾股定理即可求得MP的长.
【解答】解:根据条件可知:BP=×32=16(海里),BM=×36=18(海里).
∵∠MBP=180﹣60﹣30=90°
则△BPM是直角三角形.
∴MP===2(海里)
答:M岛与P岛之间的距离是2海里.
【点评】本题主要考查了勾股定理,正确证明△BPM是直角三角形是解决本题的关键.
20.(8分)周末,小明坐公交车到文华公园游玩,他从家出发0.8小时后到达书城,停留一段时间后继续坐公交车到文华公园,在小明离家一段时间后,爸爸驾车沿相同的路线前往文华公园,如图是他们离家的路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是 小明离家的时间 ,因变量是 他们离家的路程 ;小明家到文华公园的路程为 30 km;
(2)小明书城停留的时间为 1.7 h,小明从家出发到达文化公园的平均速度为 7.5 km/h;
(3)图中的B点表示 爸爸出发1小时后到达文华公园 ;
(4)爸爸驾车经过多久追上小明?此时距离文华公园多远?
【分析】(1)根据图象进行判断,即可得出自变量与因变量、路程;
(2)根据图象中数据进行计算,即可得到时间、速度;
(3)根据自变量、因变量表示的意义以及B点坐标即可得到B点坐标表示的意义;
(4)根据相应的路程除以时间,即可得出两人速度,再根据追击问题关系式即可解答.
【解答】解:(1)由图象可得,自变量是小明离家的时间,因变量是他们离家的路程,小明家到文华公园的路程为30km,
故答案为:小明离家的时间,他们离家的路程,30;
(2)由图象可得,小明在中心书城逗留的时间为2.5﹣0.8=1.7(h),小明从家出发到达文化公园的平均速度为:=7.5(km/h),
故答案为:1.7,7.5;
(3)由图象可得,B点坐标为(3.5,30),表示爸爸出发3.5﹣2.5=1(小时)后到达文华公园,或小明离家3.5小时时,爸爸到达文华公园,或爸爸离家的路程为30km;
(4)由图象可得,小明从书城到公园的平均速度为=12(km/h),
小明爸爸驾车的平均速度为=30(km/h),
爸爸驾车经过=h追上小明,
30﹣30×=10(km);
方法二:设爸爸出发后mh追上小明,根据题意得:
30m﹣12m=12,
解得:m=,
30﹣30×=10(km),
即爸爸驾车经过小时追上小明,此时距离文华公园10km.
【点评】本题考查了函数的图象,以及行程问题的数量关系的运用,解题关键是正确理解清楚函数图象的意义.
21.(8分)已知,如图,在平面直角坐标系中,S△ABC=24,OA=OB,BC=12,求△ABC三个顶点的坐标.
【分析】首先根据面积求得OA的长,再根据已知条件求得OB的长,最后求得OC的长.最后写坐标的时候注意点的位置.
【解答】解:∵S△ABC=BC OA=24,OA=OB,BC=12,
∴OA=OB===4,
∴OC=8,
∵点O为原点,
∴A(0,4),B(﹣4,0),C(8,0).
【点评】写点的坐标的时候,特别注意根据点所在的位置来确定坐标符号.
22.(10分)如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE,DE,DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=15°,求∠BDC的度数.
【分析】(1)通过SAS直角即可证明;
(2)由外角的性质可得∠AEB=∠ACB+∠CAE=15°+45°=60°,再借助全等三角形的性质即可得出答案.
【解答】(1)证明:在△ABE与△CBD中,
,
∴△ABE≌△CBD(SAS);
(2)在△ABC中,
∵AB=CB,∠ABC=90°,
∴∠BAC=∠ACB=45°,
由(1)得:△ABE≌△CBD(SAS),
∴∠AEB=∠BDC,
∵∠AEB为△AEC的外角,
∴∠AEB=∠ACB+∠CAE=15°+45°=60°,
∴∠BDC=60°.
【点评】本题主要考查了全等三角形的判定与性质,三角形外角的性质等知识,证明△ABE≌△CBD是解题的关键.
23.(10分)先阅读下列的解答过程,然后再解答:
形如的化简,只要我们找到两个数a、b,使a+b=m,ab=n,使得=m,,
那么便有:(a>b)
例如:化简.
解:首先把化为,这里m=7,n=12,由于4+3=7,4×3=12即=7,;
∴.
由上述例题的方法化简:.
【分析】根据题意利用二次根式的性质进行化简即可得出答案.
【解答】解:
=
=
=
=||
=.
【点评】本题主要考查了二次根式的化简,掌握二次根式的性质是解题的关键.
一、选择题(每小题3分,共30分)
1.(3分)下列四组数据中,不能作为直角三角形的三边长的是( )
A.3,4,6 B.7,24,25 C.6,8,10 D.9,12,15
2.(3分)在﹣,2π,,,0,中无理数个数为( )
A.1个 B.2个 C.3个 D.4个
3.(3分)分析下列说法:①实数与数轴上的点一一对应;②﹣a2没有平方根;③任何实数的立方根有且只有一个;④平方根与立方根相同的数是0和1.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.(3分)在平面直角坐标系中,点(1,﹣3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(3分)下列计算正确的是( )
A. B.
C. D.
6.(3分)如图,在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是( )
A.(2,1) B.(1,2) C.(,1) D.(1,)
7.(3分)已知m+n=2,mn=﹣2,则(1﹣m)(1﹣n)的值为( )
A.﹣3 B.﹣1 C.1 D.5
8.(3分)如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )
A. B.
C. D.
9.(3分)已知直线l1∥l2,将含30°角的直角三角板按如图所示摆放.若∠1=120°,则∠2=( )
A.120° B.130° C.140° D.150°
10.(3分)估计+3的值( )
A.在5和6之间 B.在6和7之间 C.在7和8之间 D.在8和9之间
二、填空题(每小题3分,共15分)
11.(3分)比较大小:﹣3 ﹣2.
12.(3分)已知点A(2,y)与点B(x,﹣3)关于x轴对称,则xy= .
13.(3分)已知实数a,b满足(a﹣2)2+=0,那么(b﹣a)的立方根是 .
14.(3分)如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为 cm.
15.(3分)如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿着直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为 cm.
三、计算题(每题3分,共18分)
16.(18分)(1);
(2);
(3);
(4)(1+2x)3﹣=1;
(5)2;
(6).
四、解答题(共30分)
17.(6分)已知x﹣1的平方根是±3,2x+y+7的立方根是2,求7﹣x﹣y的平方根.
18.(7分)如图,有一空心圆柱,高为12cm,底面周长为15cm,在圆柱内的下底面A处有一只蝴蝶,它想和上底面B处的同伴汇合,则这只蝴蝶经过的最短距离是多少cm?(π取3)
19.(8分)如图所示,缉毒警方在基地B处获知有贩毒分子分别在P岛和M岛进行毒品交易后,缉毒艇立即出发,已知甲艇沿北偏东60°方向以每小时36海里的速度前进,乙艇沿南偏东30°方向以每小时32海里的速度前进,半小时后甲到M岛,乙到P岛,则M岛与P岛之间的距离是多少?(结果保留根号)
20.(8分)周末,小明坐公交车到文华公园游玩,他从家出发0.8小时后到达书城,停留一段时间后继续坐公交车到文华公园,在小明离家一段时间后,爸爸驾车沿相同的路线前往文华公园,如图是他们离家的路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是 ,因变量是 ;小明家到文华公园的路程为 km;
(2)小明书城停留的时间为 h,小明从家出发到达文化公园的平均速度为 km/h;
(3)图中的B点表示 ;
(4)爸爸驾车经过多久追上小明?此时距离文华公园多远?
21.(8分)已知,如图,在平面直角坐标系中,S△ABC=24,OA=OB,BC=12,求△ABC三个顶点的坐标.
22.(10分)如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE,DE,DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=15°,求∠BDC的度数.
23.(10分)先阅读下列的解答过程,然后再解答:
形如的化简,只要我们找到两个数a、b,使a+b=m,ab=n,使得=m,,
那么便有:(a>b)
例如:化简.
解:首先把化为,这里m=7,n=12,由于4+3=7,4×3=12即=7,;
∴.
由上述例题的方法化简:.
2022-2023学年河南省郑州市郑东新区外国语学校八年级(上)开学数学试卷
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.(3分)下列四组数据中,不能作为直角三角形的三边长的是( )
A.3,4,6 B.7,24,25 C.6,8,10 D.9,12,15
【分析】判断是否为直角三角形,只要验证两小边的平方和等于最长边的平方即可.
【解答】解:A、32+42≠62,不能组成直角三角形,符合题意;
B、72+242=252,能组成直角三角形,不符合题意;
C、62+82=102,能组成直角三角形,不符合题意;
D、92+122=152,能组成直角三角形,不符合题意.
故选:A.
【点评】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
2.(3分)在﹣,2π,,,0,中无理数个数为( )
A.1个 B.2个 C.3个 D.4个
【分析】由于开不尽方才是无理数,无限不循环小数为无理数,所以根据无理数的定义即可判定选择项.
【解答】解:在﹣,2π,,,0,中,
根据无理数的定义可得,无理数有2π,,三个.
故选:C.
【点评】此题主要考查了无理数定义.解题时注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,,0.8080080008…(每两个8之间依次多1个0)等形式.
3.(3分)分析下列说法:①实数与数轴上的点一一对应;②﹣a2没有平方根;③任何实数的立方根有且只有一个;④平方根与立方根相同的数是0和1.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】本题考查实数与数轴的点的关系及实数的有关性质,依次分析可得答案.
【解答】解:依次分析可得:
①实数与数轴上的点一一对应,符合实数与数轴上的点的关系,正确;
②a=0时,﹣a2=0,平方根为0,故错误;
③任何实数的立方根有且只有一个,正确;
④平方根与立方根相同的数是0,而1的平方根是±1,而立方根是1,不正确.
①③正确,
故选:B.
【点评】本题考查实数与数轴的点的关系及实数的有关性质.
4.(3分)在平面直角坐标系中,点(1,﹣3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据各象限内点的坐标特征解答.
【解答】解:点(1,﹣3)在第四象限.
故选:D.
【点评】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
5.(3分)下列计算正确的是( )
A. B.
C. D.
【分析】根据二次根式的混合运算法则即可直接解题.
【解答】解:A、非同类二次根式的被开方数不能直接相减,故错误.
B、∵π>3,被开方数的算术平方根为非负数,故错误.
C、=≠3,故错误.
D、==,故正确.
故选:D.
【点评】本题考查了二次根式的混合运算,难度不大,重点掌握二次根式的混合运算法则.
6.(3分)如图,在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是( )
A.(2,1) B.(1,2) C.(,1) D.(1,)
【分析】首先过点A作AC⊥OB于点C,由△AOB是等边三角形,若B点的坐标是(2,0),可求得OA=OB=2,OC=1,然后由勾股定理求得AC的长,则可求得答案.
【解答】解:过点A作AC⊥OB于点C,
∵B点的坐标是(2,0),
∴OB=2,
∵△AOB是等边三角形,
∴OA=OB=2,OC=OB=1,
在Rt△OAC中,AC==,
∴A点的坐标是:(1,).
故选:D.
【点评】此题考查了等边三角形的性质以及勾股定理.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.
7.(3分)已知m+n=2,mn=﹣2,则(1﹣m)(1﹣n)的值为( )
A.﹣3 B.﹣1 C.1 D.5
【分析】多项式乘多项式法则,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积转换成以m+n,mn为整体相加的形式,代入求值.
【解答】解:∵m+n=2,mn=﹣2,
∴(1﹣m)(1﹣n),
=1﹣(m+n)+mn,
=1﹣2﹣2,
=﹣3.
故选:A.
【点评】本题考查了多项式乘多项式法则,合并同类项时要注意项中的指数及字母是否相同.
8.(3分)如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )
A. B.
C. D.
【分析】根据全等三角形的判定定理进行判断.
【解答】解:A、由全等三角形的判定定理SAS证得图中两个小三角形全等,
故本选项不符合题意;
B、由全等三角形的判定定理SAS证得图中两个小三角形全等,
故本选项不符合题意;
C、如图1,∵∠DEC=∠B+∠BDE,
∴x°+∠FEC=x°+∠BDE,
∴∠FEC=∠BDE,
所以其对应边应该是BE和CF,而已知给的是BD=FC=3,
所以不能判定两个小三角形全等,故本选项符合题意;
D、如图2,∵∠DEC=∠B+∠BDE,
∴x°+∠FEC=x°+∠BDE,
∴∠FEC=∠BDE,
∵BD=EC=2,∠B=∠C,
∴△BDE≌△CEF,
所以能判定两个小三角形全等,故本选项不符合题意;
由于本题选择可能得不到全等三角形纸片的图形,
故选:C.
【点评】本题考查了全等三角形的判定,注意三角形边和角的对应关系是关键.
9.(3分)已知直线l1∥l2,将含30°角的直角三角板按如图所示摆放.若∠1=120°,则∠2=( )
A.120° B.130° C.140° D.150°
【分析】过点B作BF∥l1,交AC于点F,利用三角形的外角的性质,平行线的性质定理和对顶角相等的性质解答即可.
【解答】解:过含30°角的直角三角板的直角顶点B作BF∥l1,交AC于点F,
∵∠C=30°,
∴∠A=90°﹣∠C=60°.
∵∠1=∠A+∠ADE,
∴∠ADE=60°.
∵BF∥l1,
∴∠ABF=∠ADE=60°,
∴∠FBG=90°﹣∠ABF=30°.
∵BF∥l1,l1∥l2,
∴BF∥l2,
∴∠BGH+∠FBG=180°,
∴∠BGH=180°﹣∠FBG=150°,
∴∠2=∠BGH=150°.
故选:D.
【点评】本题主要考查了直角三角形的两个锐角互余,平行线的性质定理,三角形的外角的性质,对顶角相等,过点B作BF∥l1,交AC于点F是解题的关键.
10.(3分)估计+3的值( )
A.在5和6之间 B.在6和7之间 C.在7和8之间 D.在8和9之间
【分析】先估计的整数部分,然后即可判断+3的近似值.
【解答】解:∵42=16,52=25,
所以,
所以+3在7到8之间.
故选:C.
【点评】此题主要考查了估算无理数的大小的能力,理解无理数性质,估算其数值.现实生活中经常需要估算,估算应是我们具备的数学能力,“夹逼法”是估算的一般方法,也是常用方法.
二、填空题(每小题3分,共15分)
11.(3分)比较大小:﹣3 < ﹣2.
【分析】先把两数平方,再根据实数比较大小的方法即可比较大小.
【解答】解:∵(3)2=18,(2)2=12,
∴﹣3<﹣2.
故答案为:<.
【点评】此题主要考查了实数的大小的比较,实数大小比较法则:
(1)正数大于0,0大于负数,正数大于负数;
(2)两个负数,绝对值大的反而小.
12.(3分)已知点A(2,y)与点B(x,﹣3)关于x轴对称,则xy= 6 .
【分析】根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变,可得到x、y的值,进而计算出答案.
【解答】解:∵点A(2,y)与点B(x,﹣3)关于y轴对称,
∴x=﹣2,y=﹣3,
∴xy=6,
故答案为:6.
【点评】此题主要考查了关于y轴对称点的坐标特点,关键是掌握点的变化规律.
13.(3分)已知实数a,b满足(a﹣2)2+=0,那么(b﹣a)的立方根是 ﹣2 .
【分析】根据非负数的性质即可求出a与b的值,然后代入b﹣a即可求出答案.
【解答】解:由题意可知:a﹣2=0,b+6=0,
∴a=2,b=﹣6,
∴b﹣a=﹣6﹣2=﹣8,
∴﹣8的立方根是﹣2.
故答案为:﹣2.
【点评】本题考查立方根的定义,解题的关键是熟练运用立方根的定义,本题属于基础题型.
14.(3分)如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为 13 cm.
【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将长方体展开,然后利用两点之间线段最短解答.
【解答】解:
∵PA=2×(4+2)=12,QA=5
∴PQ=13.
故答案为:13.
【点评】本题主要考查两点之间线段最短,以及如何把立体图形转化成平面图形.
15.(3分)如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿着直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为 3 cm.
【分析】由折叠的性质知CD=DE,AC=AE.根据题意在Rt△BDE中运用勾股定理求DE.
【解答】解:由勾股定理得,AB=10.
由折叠的性质知,AE=AC=6,DE=CD,∠AED=∠C=90°.
∴BE=AB﹣AE=10﹣6=4,
在Rt△BDE中,由勾股定理得,
DE2+BE2=BD2
即CD2+42=(8﹣CD)2,
解得:CD=3cm.
【点评】本题利用了:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、勾股定理求解.
三、计算题(每题3分,共18分)
16.(18分)(1);
(2);
(3);
(4)(1+2x)3﹣=1;
(5)2;
(6).
【分析】(1)根据完全平方公式计算即可求解;
(2)根据二次根式乘除法运算的计算法则计算即可求解;
(3)先算小括号里面的减法,再算括号外面的乘法;
(4)先移项,再合并同类项,再开立方即可求解;
(5)先化简,再计算加法;
(6)先化简,再计算加减法.
【解答】解:(1)
=1﹣4+8
=9﹣4;
(2)
=
=;
(3)
=(3﹣4)×
=﹣×
=﹣3;
(4)(1+2x)3﹣=1,
(1+2x)3=+1,
(1+2x)3=,
1+2x=,
2x=﹣1,
2x=,
x=;
(5)2
=4+12
=16;
(6)
=5+﹣18﹣
=﹣13.
【点评】本题考查了二次根式的混合运算,在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.同时考查了立方根.
四、解答题(共30分)
17.(6分)已知x﹣1的平方根是±3,2x+y+7的立方根是2,求7﹣x﹣y的平方根.
【分析】根据题意分别确定x﹣1及2x+y+7的值,继而化简后可得出答案.
【解答】解:由题意得:x﹣1=9①,2x+y+7=8②,
②﹣①得:x+y+8=﹣1,
∴x+y=﹣9,
∴7﹣x﹣y=7﹣(x+y)=16,
它的平方根为±4.
【点评】本题考查了平方根及立方根的知识,比较简单,注意一个正数的平方根有两个.
18.(7分)如图,有一空心圆柱,高为12cm,底面周长为15cm,在圆柱内的下底面A处有一只蝴蝶,它想和上底面B处的同伴汇合,则这只蝴蝶经过的最短距离是多少cm?(π取3)
【分析】先把圆柱的侧面展开得其侧面展开图,则A,B所在的长方形的长为圆柱的高12cm,宽为底面圆周长的一半为πr,蝴蝶经过的最短距离为连接A,B的线段长,由勾股定理求得AB的长.
【解答】解:如图,将圆柱的侧面沿过A点的一条母线剪开,得到长方形ADFE,
连接AB,则线段AB的长就是蝴蝶爬行的最短距离,其中C,B分别是AE,DF的中点.
∵AD=12cm,DB=πr=7.5cm,
∴AB故蝴蝶经过的最短距离为:(cm).
答:这只蝴蝶经过的最短距离是cm.
【点评】此题考查平面展开﹣最短路径问题,关键是根据勾股定理解答.
19.(8分)如图所示,缉毒警方在基地B处获知有贩毒分子分别在P岛和M岛进行毒品交易后,缉毒艇立即出发,已知甲艇沿北偏东60°方向以每小时36海里的速度前进,乙艇沿南偏东30°方向以每小时32海里的速度前进,半小时后甲到M岛,乙到P岛,则M岛与P岛之间的距离是多少?(结果保留根号)
【分析】根据条件可以证得△BMN是直角三角形,求得BP与BM的长,根据勾股定理即可求得MP的长.
【解答】解:根据条件可知:BP=×32=16(海里),BM=×36=18(海里).
∵∠MBP=180﹣60﹣30=90°
则△BPM是直角三角形.
∴MP===2(海里)
答:M岛与P岛之间的距离是2海里.
【点评】本题主要考查了勾股定理,正确证明△BPM是直角三角形是解决本题的关键.
20.(8分)周末,小明坐公交车到文华公园游玩,他从家出发0.8小时后到达书城,停留一段时间后继续坐公交车到文华公园,在小明离家一段时间后,爸爸驾车沿相同的路线前往文华公园,如图是他们离家的路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是 小明离家的时间 ,因变量是 他们离家的路程 ;小明家到文华公园的路程为 30 km;
(2)小明书城停留的时间为 1.7 h,小明从家出发到达文化公园的平均速度为 7.5 km/h;
(3)图中的B点表示 爸爸出发1小时后到达文华公园 ;
(4)爸爸驾车经过多久追上小明?此时距离文华公园多远?
【分析】(1)根据图象进行判断,即可得出自变量与因变量、路程;
(2)根据图象中数据进行计算,即可得到时间、速度;
(3)根据自变量、因变量表示的意义以及B点坐标即可得到B点坐标表示的意义;
(4)根据相应的路程除以时间,即可得出两人速度,再根据追击问题关系式即可解答.
【解答】解:(1)由图象可得,自变量是小明离家的时间,因变量是他们离家的路程,小明家到文华公园的路程为30km,
故答案为:小明离家的时间,他们离家的路程,30;
(2)由图象可得,小明在中心书城逗留的时间为2.5﹣0.8=1.7(h),小明从家出发到达文化公园的平均速度为:=7.5(km/h),
故答案为:1.7,7.5;
(3)由图象可得,B点坐标为(3.5,30),表示爸爸出发3.5﹣2.5=1(小时)后到达文华公园,或小明离家3.5小时时,爸爸到达文华公园,或爸爸离家的路程为30km;
(4)由图象可得,小明从书城到公园的平均速度为=12(km/h),
小明爸爸驾车的平均速度为=30(km/h),
爸爸驾车经过=h追上小明,
30﹣30×=10(km);
方法二:设爸爸出发后mh追上小明,根据题意得:
30m﹣12m=12,
解得:m=,
30﹣30×=10(km),
即爸爸驾车经过小时追上小明,此时距离文华公园10km.
【点评】本题考查了函数的图象,以及行程问题的数量关系的运用,解题关键是正确理解清楚函数图象的意义.
21.(8分)已知,如图,在平面直角坐标系中,S△ABC=24,OA=OB,BC=12,求△ABC三个顶点的坐标.
【分析】首先根据面积求得OA的长,再根据已知条件求得OB的长,最后求得OC的长.最后写坐标的时候注意点的位置.
【解答】解:∵S△ABC=BC OA=24,OA=OB,BC=12,
∴OA=OB===4,
∴OC=8,
∵点O为原点,
∴A(0,4),B(﹣4,0),C(8,0).
【点评】写点的坐标的时候,特别注意根据点所在的位置来确定坐标符号.
22.(10分)如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE,DE,DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=15°,求∠BDC的度数.
【分析】(1)通过SAS直角即可证明;
(2)由外角的性质可得∠AEB=∠ACB+∠CAE=15°+45°=60°,再借助全等三角形的性质即可得出答案.
【解答】(1)证明:在△ABE与△CBD中,
,
∴△ABE≌△CBD(SAS);
(2)在△ABC中,
∵AB=CB,∠ABC=90°,
∴∠BAC=∠ACB=45°,
由(1)得:△ABE≌△CBD(SAS),
∴∠AEB=∠BDC,
∵∠AEB为△AEC的外角,
∴∠AEB=∠ACB+∠CAE=15°+45°=60°,
∴∠BDC=60°.
【点评】本题主要考查了全等三角形的判定与性质,三角形外角的性质等知识,证明△ABE≌△CBD是解题的关键.
23.(10分)先阅读下列的解答过程,然后再解答:
形如的化简,只要我们找到两个数a、b,使a+b=m,ab=n,使得=m,,
那么便有:(a>b)
例如:化简.
解:首先把化为,这里m=7,n=12,由于4+3=7,4×3=12即=7,;
∴.
由上述例题的方法化简:.
【分析】根据题意利用二次根式的性质进行化简即可得出答案.
【解答】解:
=
=
=
=||
=.
【点评】本题主要考查了二次根式的化简,掌握二次根式的性质是解题的关键.
同课章节目录
