2013-2014学年九年级数学上册期中检测题(含详解)
文档属性
| 名称 | 2013-2014学年九年级数学上册期中检测题(含详解) |  | |
| 格式 | zip | ||
| 文件大小 | 519.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-15 08:40:47 | ||
图片预览


文档简介
期中检测题
(本检测题满分:120分 时间:120分钟)
选择题(每小题3分,共36分)
1.如图,在平行四边形中,对角线相交于点 O,若
的和为18 cm,,△的周长为13 cm,
则的长是( )
A.6 cm B.9 cm C.3 cm D.12 cm
2.一个等腰梯形的两底之差为,高为,则等腰梯形的锐角为( )
A. B. C. D.
3.如图,在菱形纸片中,,折叠菱形纸片,使点落在(为中点)所在直线处,得到经过点的折痕.则 的大小为( )
A. B. C. D.
4.如图,在梯形中,∥,,分别是的中点,若
5 cm,13 cm,则EF=( )
A.4 cm B.5 cm C.6.5 cm D.9 cm
5. 如图,在平面直角坐标系中,将点(-2,3)向右平移3个单位长度后,
对应的点A′的坐标是( )
A. B. C. D.
6.从菱形的钝角顶点向对角的两条边作垂线,垂足恰好是该边的中点,则菱形的内角中钝角的度数是( )
A. B. C. D.
7.顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形满足条件的是( )
①平行四边形; ②菱形; ③等腰梯形 ;④对角线互相垂直的四边形.
A.①③ B.②③
C.③④ D.②④
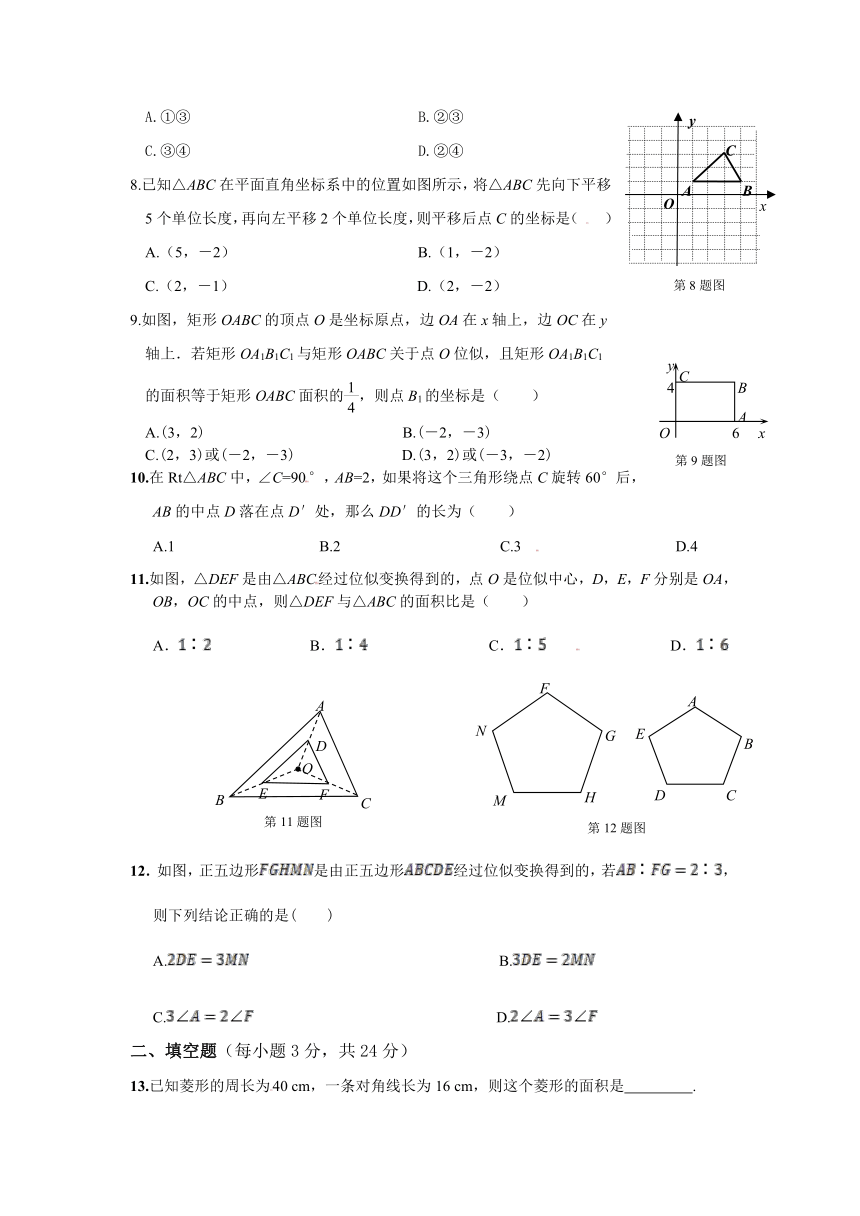
8.已知△ABC在平面直角坐标系中的位置如图所示,将△ABC先向下平移
5个单位长度,再向左平移2个单位长度,则平移后点C的坐标是( )
A.(5,-2) B.(1,-2)
C.(2,-1) D.(2,-2)
9.如图,矩形OABC的顶点O是坐标原点,边OA在x轴上,边OC在y
轴上.若矩形OA1B1C1与矩形OABC关于点O位似,且矩形OA1B1C1
的面积等于矩形OABC面积的,则点B1的坐标是( )
A.(3,2) B.(-2,-3)
C.(2,3)或(-2,-3) D.(3,2)或(-3,-2)
10.在Rt△ABC中,∠C=90°,AB=2,如果将这个三角形绕点C旋转60°后,
AB的中点D落在点D′处,那么DD′的长为( )
A.1 B.2 C.3 D.4
11.如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是( )
A. B. C. D.
12.如图,正五边形是由正五边形经过位似变换得到的,若,
则下列结论正确的是( )
A. B.
C. D.
二、填空题(每小题3分,共24分)
13.已知菱形的周长为40 cm,一条对角线长为16 cm,则这个菱形的面积是 .
14.在矩形中,对角线交于点,若∠,则 .
15.如图,把两个大小完全相同的矩形拼成“L”型图案,则___ __,_____.
16.将点沿轴向右平移3个单位长度,再沿轴向下平移4个长度单位后得到点的坐标为 .
17.在平行四边形、菱形、矩形、正方形中,能够找到一个点,使该点到各顶点距离相等的
图形是________.
18.如图,在矩形中,,在上取一点,将向上折叠,使点落
在上的点.若四边形与矩形相似,则 .
19.如图,边长为2的正方形的对角线相交于点,过点的直线分别交于,则阴影部分的面积是 .
20.在平面直角坐标系中,线段的端点的坐标为,将其先向右平移个单位长度,再向下平移个单位长度,得到线段,则点对应点的坐标为____ __.
三、解答题(共60分)
21.(8分)如图,在四边形中,, QUOTE ,
,垂足分别为,
求证:四边形是平行四边形.
22.(10分)辨析纠错
已知:如图,在△中,是的平分线,∥,∥.
求证:四边形是菱形.
对于这道题,小明是这样证明的:
证明:∵平分,∴ ∠1=∠2(角平分线的定义).
∵ ∥,∴ ∠2=∠3(两直线平行,内错角相等).
∴ ∠1=∠3(等量代换).∴ (等角对等边).
同理可证:∴ 四边形是菱形(菱形的定义).
老师说小明的证明过程有错误.
(1)请你帮小明指出他的错误是什么.
(2)请你帮小明做出正确的解答.
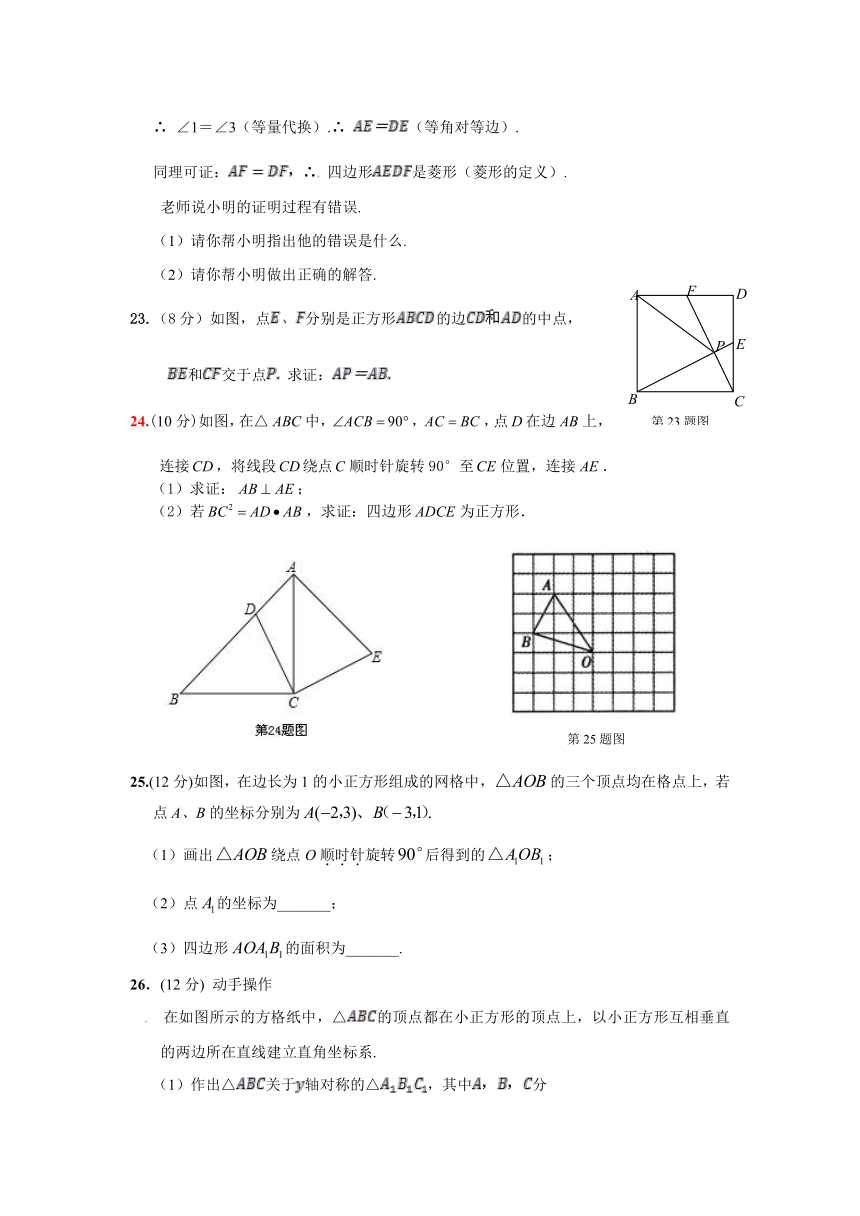
23.(8分)如图,点分别是正方形的边的中点,
和交于点 求证:
24.(10分)如图,在△中,,,点在边上,
连接,将线段绕点顺时针旋转90°至位置,连接.
(1)求证:;
(2)若,求证:四边形为正方形.
25.(12分)如图,在边长为1的小正方形组成的网格中,的三个顶点均在格点上,若点A、B的坐标分别为
(1)画出绕点O顺时针旋转后得到的;
(2)点的坐标为_______;
(3)四边形的面积为_______.
26.(12分) 动手操作
在如图所示的方格纸中,△的顶点都在小正方形的顶点上,以小正方形互相垂直的两边所在直线建立直角坐标系.
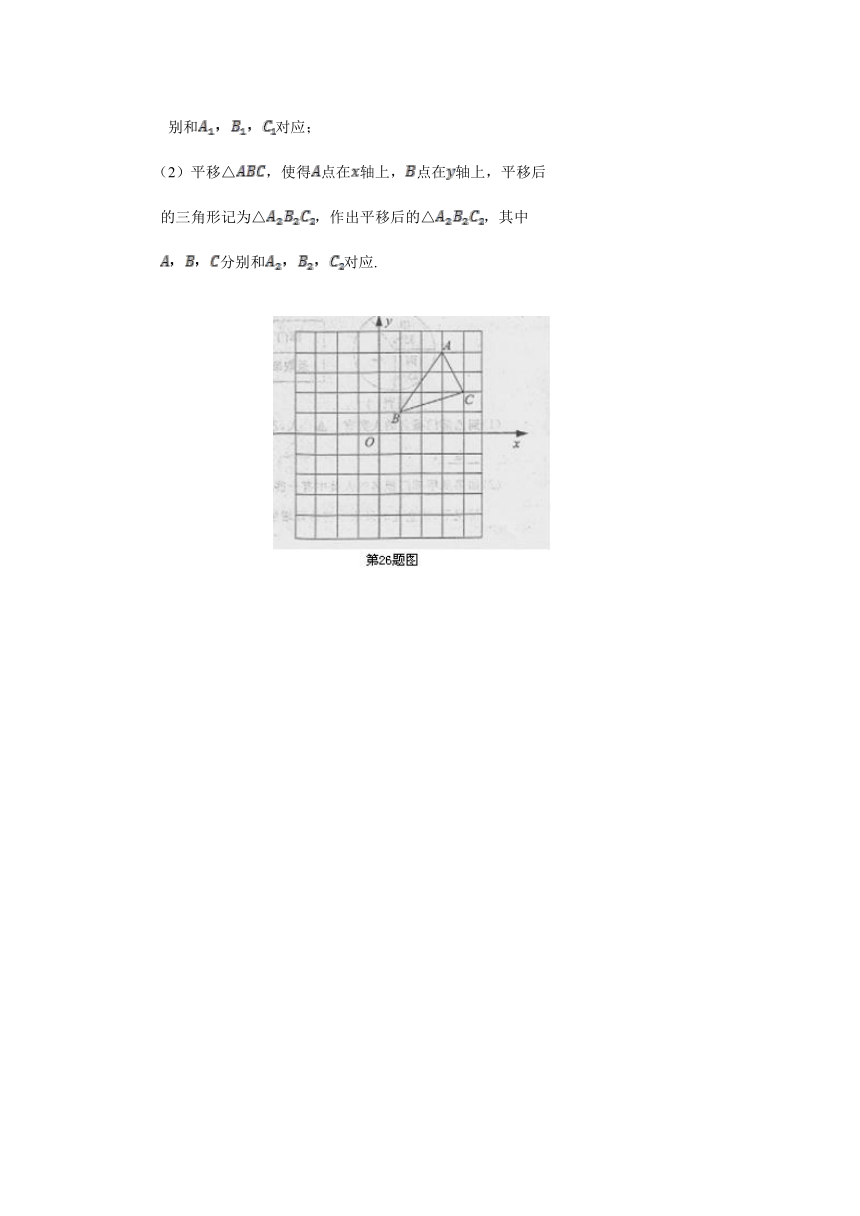
(1)作出△关于轴对称的△,其中分
别和对应;
(2)平移△,使得点在轴上,点在轴上,平移后
的三角形记为△,作出平移后的△,其中
分别和对应.
期中检测题参考答案
1.A 解析:因为18 cm , 所以.
因为△的周长为13 cm , 所以
又因为, 所以6 cm.
2.B 解析:如图,在等腰梯形中,
高则所以∠,故选B.
3.B 解析:连接,∵ 四边形为菱形,,
∴ 为等边三角形,,.
∵ 为的中点,∴ 为的平分线,
即,∴ .
由折叠的性质得.
在△中,.故选B.
4.A 解析:如图,作∥∥, 因为,
所以∠
因为四边形和四边形都是平行四边形,
所以
又因为5 cm,13 cm,所以8 cm,.
根据直角三角形斜边上的中线等于斜边的一半,得4 cm .
5.C 解析:根据题意,从点向右平移3个单位长度到点′,点′的纵坐标不变,横坐标是,故点′的坐标是(1,3).故选C.
6.C 解析:如图,在菱形中,,
连接,
因为是的中垂线,所以.
所以△是等边三角形,
所以∠=60°,从而∠.
7. D 解析:顺次连接一个四边形的各边中点,得到了一个矩形,则该四边形需
满足的条件是对角线互相垂直.
8. B 解析:点C的坐标变化依次为.
9. D 解析:由矩形OA1B1C1的面积等于矩形OABC面积的,知矩形OA1B1C1与
矩形OABC的位似比是1∶2,又知点当两矩形在点同侧时,;
当两矩形在点异侧时,.
10. A 11. B 12. B
13. 解析:如图,菱形的周长为40 cm,=16 cm,
则10 cm,8 cm.
又,所以6 cm.
所以菱形的面积为=.
14.40° 解析:由矩形的性质知,,所以∠∠.
又∠所以∠
15.90° 45° 解析:由矩形的性质知∠
所以∠.
16.(2,-2) 解析:根据点的平移规律:左右平移,横坐标减加,纵坐标不变;上下平移,纵坐标加减,横坐标不变即可得到.
由题意可知点的坐标是(-1+3,2-4),即(2,-2).
17.矩形和正方形
18. 解析:可设,由四边形与矩形相似,根据相似多边形对应边的比相等列出比例式求解即可.
∵,设,则,.
∵ 四边形与矩形相似,∴ ,即,
解得(不合题意舍去).
经检验是原方程的解.
19.1 解析:△绕点旋转后与△重合,所以阴影部分的面积等于正方形面积的,即1.
20. 解析:.
21. 证明:因为,,所以∠∠.
因为所以,所以
因为△≌△,
所以∠ =∠,所以∥.
又因为,所以四边形是平行四边形.
22.解:⑴小明错用了菱形的定义.
⑵改正:∵ DE∥AC,DF∥AB,∴ 四边形是平行四边形,∴ ∠3=∠2.
∵ 平分∠,∴ ∠1=∠2,∴ ∠1=∠3.
∴ ,∴ 平行四边形是菱形.
23.证明:如图,延长交于点.
因为, ∠∠,
所以△≌△,所以 ∠=∠,
从而∠+∠=∠∠,
所以.
再由得△≌△,
从而,即.
在Rt△中,由直角三角形斜边上的中线等于斜边的一半,得
,即.
24.证明:(1)∵ ,,∴ .
∵ 线段绕点顺时针旋转90°至位置,∴ .
∵ ,∴ ,即.
在△和△中,∴ .
∴ ,∴ ,∴ .
(2)∵ ,而,∴ .
∵ ,∴ ,∴ .
而,,∴ 四边形为矩形.
∵ ,∴ 四边形为正方形.
25.解:(1)如图所示;
(2)(3,2);(3)8.
26.解:(1)(2)如图所示.
A
B
C
D
O
第1题图
E
A
D
B
C
F
第4题图
A
B
C
O
x
y
第8题图
O
A
B
C
y
x
4
6
第9题图
C
A
BA
DA
OA
EA
FA
第11题图
A
B
C
D
E
F
G
H
M
N
第12题图
C
D
E
F
A
B
G
第15题图
第19题图
A
E
D
C
F
O
B
A
B
C
D
E
F
P
第23题图
第25题图
C
B
A
D
E
第2题答图
E
A
D
B
C
F
G
H
第4题答图
第13题答图
C
A
B
D
O
A
B
C
D
E
F
P
M
第23题答图
第25题答图
(本检测题满分:120分 时间:120分钟)
选择题(每小题3分,共36分)
1.如图,在平行四边形中,对角线相交于点 O,若
的和为18 cm,,△的周长为13 cm,
则的长是( )
A.6 cm B.9 cm C.3 cm D.12 cm
2.一个等腰梯形的两底之差为,高为,则等腰梯形的锐角为( )
A. B. C. D.
3.如图,在菱形纸片中,,折叠菱形纸片,使点落在(为中点)所在直线处,得到经过点的折痕.则 的大小为( )
A. B. C. D.
4.如图,在梯形中,∥,,分别是的中点,若
5 cm,13 cm,则EF=( )
A.4 cm B.5 cm C.6.5 cm D.9 cm
5. 如图,在平面直角坐标系中,将点(-2,3)向右平移3个单位长度后,
对应的点A′的坐标是( )
A. B. C. D.
6.从菱形的钝角顶点向对角的两条边作垂线,垂足恰好是该边的中点,则菱形的内角中钝角的度数是( )
A. B. C. D.
7.顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形满足条件的是( )
①平行四边形; ②菱形; ③等腰梯形 ;④对角线互相垂直的四边形.
A.①③ B.②③
C.③④ D.②④
8.已知△ABC在平面直角坐标系中的位置如图所示,将△ABC先向下平移
5个单位长度,再向左平移2个单位长度,则平移后点C的坐标是( )
A.(5,-2) B.(1,-2)
C.(2,-1) D.(2,-2)
9.如图,矩形OABC的顶点O是坐标原点,边OA在x轴上,边OC在y
轴上.若矩形OA1B1C1与矩形OABC关于点O位似,且矩形OA1B1C1
的面积等于矩形OABC面积的,则点B1的坐标是( )
A.(3,2) B.(-2,-3)
C.(2,3)或(-2,-3) D.(3,2)或(-3,-2)
10.在Rt△ABC中,∠C=90°,AB=2,如果将这个三角形绕点C旋转60°后,
AB的中点D落在点D′处,那么DD′的长为( )
A.1 B.2 C.3 D.4
11.如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是( )
A. B. C. D.
12.如图,正五边形是由正五边形经过位似变换得到的,若,
则下列结论正确的是( )
A. B.
C. D.
二、填空题(每小题3分,共24分)
13.已知菱形的周长为40 cm,一条对角线长为16 cm,则这个菱形的面积是 .
14.在矩形中,对角线交于点,若∠,则 .
15.如图,把两个大小完全相同的矩形拼成“L”型图案,则___ __,_____.
16.将点沿轴向右平移3个单位长度,再沿轴向下平移4个长度单位后得到点的坐标为 .
17.在平行四边形、菱形、矩形、正方形中,能够找到一个点,使该点到各顶点距离相等的
图形是________.
18.如图,在矩形中,,在上取一点,将向上折叠,使点落
在上的点.若四边形与矩形相似,则 .
19.如图,边长为2的正方形的对角线相交于点,过点的直线分别交于,则阴影部分的面积是 .
20.在平面直角坐标系中,线段的端点的坐标为,将其先向右平移个单位长度,再向下平移个单位长度,得到线段,则点对应点的坐标为____ __.
三、解答题(共60分)
21.(8分)如图,在四边形中,, QUOTE ,
,垂足分别为,
求证:四边形是平行四边形.
22.(10分)辨析纠错
已知:如图,在△中,是的平分线,∥,∥.
求证:四边形是菱形.
对于这道题,小明是这样证明的:
证明:∵平分,∴ ∠1=∠2(角平分线的定义).
∵ ∥,∴ ∠2=∠3(两直线平行,内错角相等).
∴ ∠1=∠3(等量代换).∴ (等角对等边).
同理可证:∴ 四边形是菱形(菱形的定义).
老师说小明的证明过程有错误.
(1)请你帮小明指出他的错误是什么.
(2)请你帮小明做出正确的解答.
23.(8分)如图,点分别是正方形的边的中点,
和交于点 求证:
24.(10分)如图,在△中,,,点在边上,
连接,将线段绕点顺时针旋转90°至位置,连接.
(1)求证:;
(2)若,求证:四边形为正方形.
25.(12分)如图,在边长为1的小正方形组成的网格中,的三个顶点均在格点上,若点A、B的坐标分别为
(1)画出绕点O顺时针旋转后得到的;
(2)点的坐标为_______;
(3)四边形的面积为_______.
26.(12分) 动手操作
在如图所示的方格纸中,△的顶点都在小正方形的顶点上,以小正方形互相垂直的两边所在直线建立直角坐标系.
(1)作出△关于轴对称的△,其中分
别和对应;
(2)平移△,使得点在轴上,点在轴上,平移后
的三角形记为△,作出平移后的△,其中
分别和对应.
期中检测题参考答案
1.A 解析:因为18 cm , 所以.
因为△的周长为13 cm , 所以
又因为, 所以6 cm.
2.B 解析:如图,在等腰梯形中,
高则所以∠,故选B.
3.B 解析:连接,∵ 四边形为菱形,,
∴ 为等边三角形,,.
∵ 为的中点,∴ 为的平分线,
即,∴ .
由折叠的性质得.
在△中,.故选B.
4.A 解析:如图,作∥∥, 因为,
所以∠
因为四边形和四边形都是平行四边形,
所以
又因为5 cm,13 cm,所以8 cm,.
根据直角三角形斜边上的中线等于斜边的一半,得4 cm .
5.C 解析:根据题意,从点向右平移3个单位长度到点′,点′的纵坐标不变,横坐标是,故点′的坐标是(1,3).故选C.
6.C 解析:如图,在菱形中,,
连接,
因为是的中垂线,所以.
所以△是等边三角形,
所以∠=60°,从而∠.
7. D 解析:顺次连接一个四边形的各边中点,得到了一个矩形,则该四边形需
满足的条件是对角线互相垂直.
8. B 解析:点C的坐标变化依次为.
9. D 解析:由矩形OA1B1C1的面积等于矩形OABC面积的,知矩形OA1B1C1与
矩形OABC的位似比是1∶2,又知点当两矩形在点同侧时,;
当两矩形在点异侧时,.
10. A 11. B 12. B
13. 解析:如图,菱形的周长为40 cm,=16 cm,
则10 cm,8 cm.
又,所以6 cm.
所以菱形的面积为=.
14.40° 解析:由矩形的性质知,,所以∠∠.
又∠所以∠
15.90° 45° 解析:由矩形的性质知∠
所以∠.
16.(2,-2) 解析:根据点的平移规律:左右平移,横坐标减加,纵坐标不变;上下平移,纵坐标加减,横坐标不变即可得到.
由题意可知点的坐标是(-1+3,2-4),即(2,-2).
17.矩形和正方形
18. 解析:可设,由四边形与矩形相似,根据相似多边形对应边的比相等列出比例式求解即可.
∵,设,则,.
∵ 四边形与矩形相似,∴ ,即,
解得(不合题意舍去).
经检验是原方程的解.
19.1 解析:△绕点旋转后与△重合,所以阴影部分的面积等于正方形面积的,即1.
20. 解析:.
21. 证明:因为,,所以∠∠.
因为所以,所以
因为△≌△,
所以∠ =∠,所以∥.
又因为,所以四边形是平行四边形.
22.解:⑴小明错用了菱形的定义.
⑵改正:∵ DE∥AC,DF∥AB,∴ 四边形是平行四边形,∴ ∠3=∠2.
∵ 平分∠,∴ ∠1=∠2,∴ ∠1=∠3.
∴ ,∴ 平行四边形是菱形.
23.证明:如图,延长交于点.
因为, ∠∠,
所以△≌△,所以 ∠=∠,
从而∠+∠=∠∠,
所以.
再由得△≌△,
从而,即.
在Rt△中,由直角三角形斜边上的中线等于斜边的一半,得
,即.
24.证明:(1)∵ ,,∴ .
∵ 线段绕点顺时针旋转90°至位置,∴ .
∵ ,∴ ,即.
在△和△中,∴ .
∴ ,∴ ,∴ .
(2)∵ ,而,∴ .
∵ ,∴ ,∴ .
而,,∴ 四边形为矩形.
∵ ,∴ 四边形为正方形.
25.解:(1)如图所示;
(2)(3,2);(3)8.
26.解:(1)(2)如图所示.
A
B
C
D
O
第1题图
E
A
D
B
C
F
第4题图
A
B
C
O
x
y
第8题图
O
A
B
C
y
x
4
6
第9题图
C
A
BA
DA
OA
EA
FA
第11题图
A
B
C
D
E
F
G
H
M
N
第12题图
C
D
E
F
A
B
G
第15题图
第19题图
A
E
D
C
F
O
B
A
B
C
D
E
F
P
第23题图
第25题图
C
B
A
D
E
第2题答图
E
A
D
B
C
F
G
H
第4题答图
第13题答图
C
A
B
D
O
A
B
C
D
E
F
P
M
第23题答图
第25题答图
同课章节目录
