12.1 全等三角形 同步过关卷(含解析)
文档属性
| 名称 | 12.1 全等三角形 同步过关卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 371.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-16 00:00:00 | ||
图片预览


文档简介
12.1全等三角形同步卷
一、单选题
1.如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=6cm,AD=5cm,那么BC的长是( )
A.4cm B.5cm C.6cm D.无法确定
2.如图,已知△ABC≌△EDF,下列结论正确的是( )
A.∠A=∠E B.∠B=∠DFE C.AC=ED D.BF=DF
3.如图,已知△ABE≌△ACD,下列选项中不能被证明的等式是( )
A.AD=AE B.DB=AE C.DF=EF D.DB=EC
4.全等图形是指两个图形( )
A.能够重合 B.形状相同 C.大小相同 D.相等
5.下列说法中正确的是( )
A.两个面积相等的图形,一定是全等图形
B.两个等边三角形是全等图形
C.两个全等图形的面积一定相等
D.若两个图形周长相等,则它们一定是全等图形
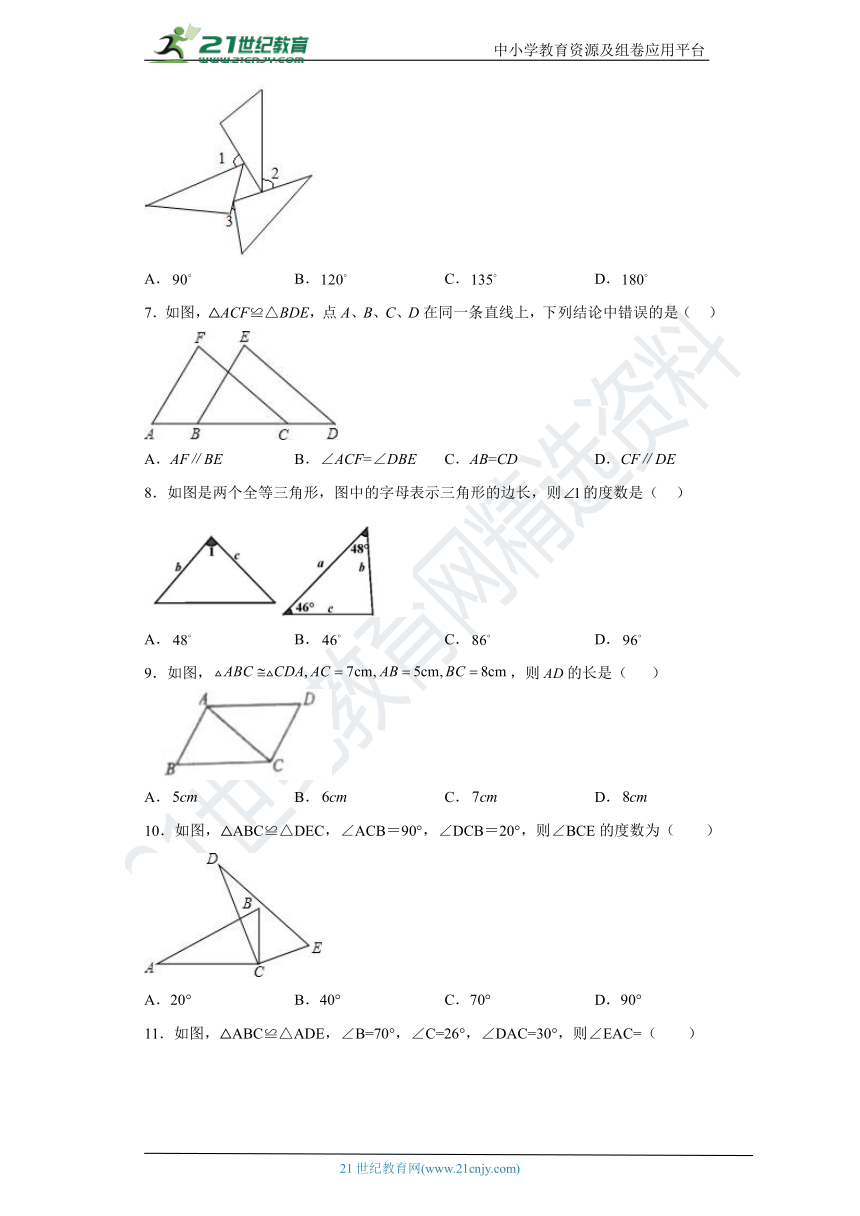
6.三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是( )
A. B. C. D.
7.如图,△ACF≌△BDE,点A、B、C、D在同一条直线上,下列结论中错误的是( )
A.AF∥BE B.∠ACF=∠DBE C.AB=CD D.CF∥DE
8.如图是两个全等三角形,图中的字母表示三角形的边长,则的度数是( )
A. B. C. D.
9.如图,,则的长是( )
A. B. C. D.
10.如图,△ABC≌△DEC,∠ACB=90°,∠DCB=20°,则∠BCE的度数为( )
A.20° B.40° C.70° D.90°
11.如图,△ABC≌△ADE,∠B=70°,∠C=26°,∠DAC=30°,则∠EAC=( )
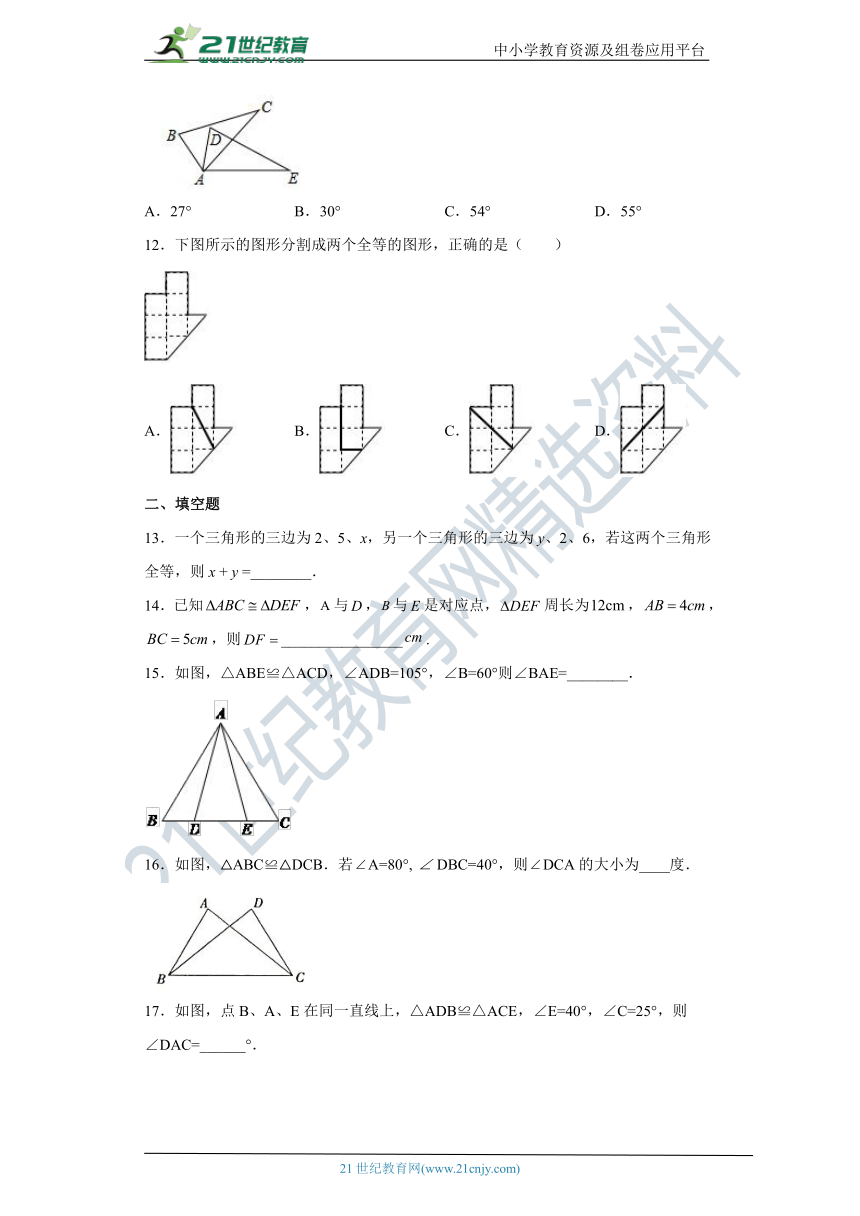
A.27° B.30° C.54° D.55°
12.下图所示的图形分割成两个全等的图形,正确的是( )
A. B. C. D.
二、填空题
13.一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x + y =________.
14.已知,与,与是对应点,周长为,,,则________________.
15.如图,△ABE≌△ACD,∠ADB=105°,∠B=60°则∠BAE=________.
16.如图,△ABC≌△DCB.若A=80°,DBC=40°,则DCA的大小为____度.
17.如图,点B、A、E在同一直线上,△ADB≌△ACE,∠E=40°,∠C=25°,则∠DAC=______°.
18.如图,△ABC≌△ADE,∠EAC=40°,则∠B=_______°.
三、解答题
19.如图△ADF≌△BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm.求:
(1)∠1的度数;(2)AC的长.
20.如图,将△ABC绕点B顺时针旋转60°后得到△BDE(点A对应点为D),线段AC交线段DE于点F.
(1)求证:∠C=∠E;
(2)求EFC的度数.
21.如图,,点在上,与相交于点,若,,,.
(1)求线段的长;
(2)求的度数.
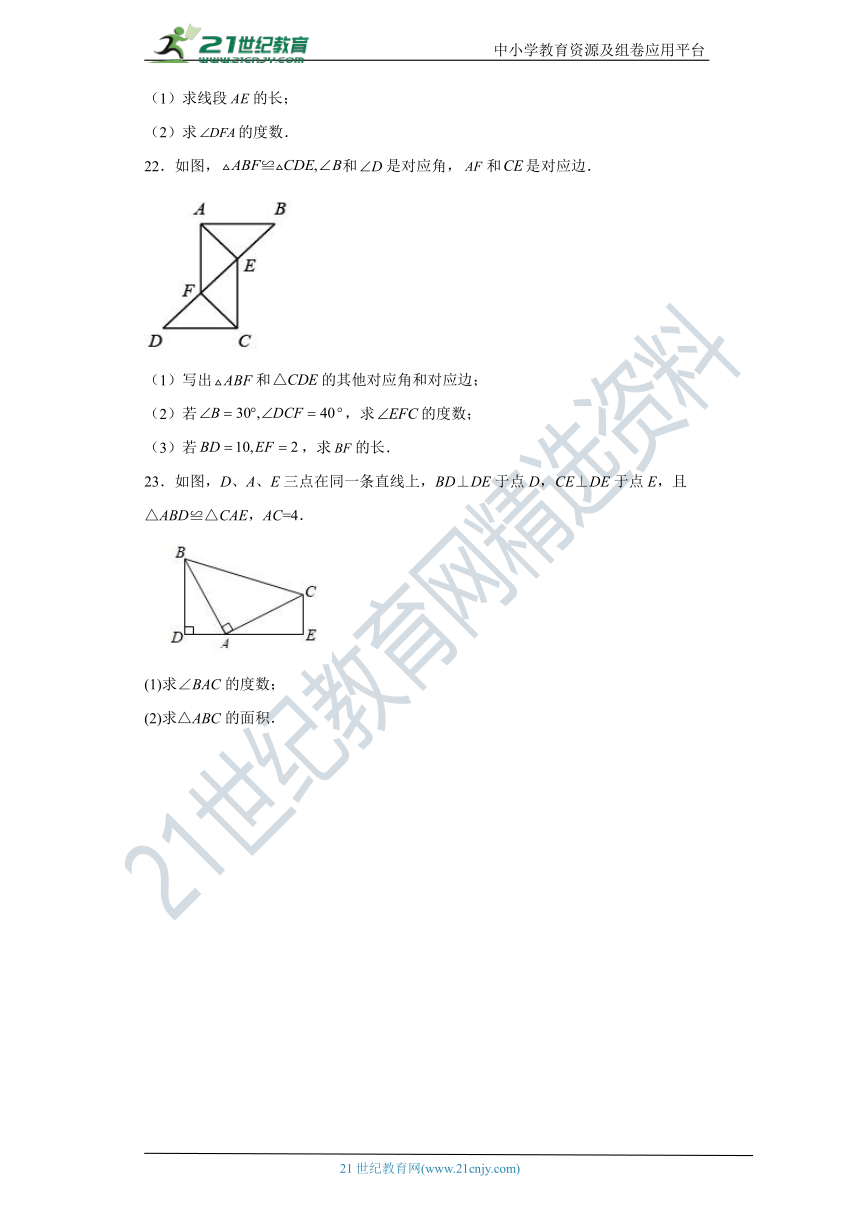
22.如图,和是对应角,和是对应边.
(1)写出和的其他对应角和对应边;
(2)若,求的度数;
(3)若,求的长.
23.如图,D、A、E三点在同一条直线上,BD⊥DE于点D,CE⊥DE于点E,且△ABD≌△CAE,AC=4.
(1)求∠BAC的度数;
(2)求△ABC的面积.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
1.B
【详解】解:∵△ABC≌△BAD,AB=6cm,BD=6cm,AD=5cm,
∴BC=AD=5cm.
故选:B.
2.A
【详解】解:∵△ABC≌△EDF,
∴∠A=∠E,A正确;
∠B=∠FDE,B错误;
AC=EF,C错误;
BF=DC,D错误;
故选A.
3.B
【详解】试题解析:∵△ABE≌△ACD,
∴AB=AC,AD=AE,∠B=∠C,故A正确;
∴AB-AD=AC-AE,即BD=EC,故D正确;
在△BDF和△CEF中
∴△BDF≌△CEF(ASA),
∴DF=EF,故C正确;
故选B.
4.A
【详解】解:根据全等图形的定义:能够重合的两个图形叫做全等图形,
故选:A.
5.C
【详解】解:A、两个面积相等的图形不一定是全等图形,故A错误;
B、两个等边三角形不一定是全等图形,故B错误;
C、两个全等图形的面积一定相等,正确;
D、若两个图形的周长相等,则它们不一定是全等形,故D错误;
故选:C.
6.D
【详解】∵图中是三个全等三角形,
∴∠4=∠8, ∠6=∠7,
又∵三角形ABC的外角和=∠1+∠2+∠3+∠4+∠5+∠6=360 ,
又∠5+∠7+∠8=180°,
∴∠1+∠2+∠3=360°-180°=180°.
故选D
7.B
【详解】解:∵△ACF≌△BDE,
∴∠A=∠EBD,
∴AF∥BE,A正确,不符合题意;
∴∠ACF=∠BDE,B错误,符合题意;
∴AC=BD,
∴AB=CD,C正确,不符合题意;
∴∠D=∠FCA,
∴CF∥DE,D正确,不符合题意;
故选B.
8.C
【详解】解:∵如图是两个全等三角形,
∴∠1=∠2=180°-48°-46°=86°.
故选:C.
9.D
【详解】解:∵△ABC≌△CDA,
∴AD=BC=8cm.
故选D.
10.C
【详解】解:∵△ABC≌△DEC,
∴∠DCE=∠ACB,
∴∠BCE=∠DCE﹣∠DCB=90°﹣20°=70°.
故选:C.
11.C
【详解】解:∵∠B=70°,∠C=26°,
∴∠BAC=180°-70°-26°=84°,
∵∠DAC=30°,
∴∠BAD=84°-30°=54°,
∵△ABC△ADE,
∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠EAC=∠BAD=54°,
故答案为C.
12.B
【详解】解:图形分割成两个全等的图形,如图所示:
故选B.
13.11
【详解】解:∵这两个三角形全等
∴x=6,y=5
∴x + y =11
故答案为11.
14.3
【详解】解:∵,,,
∴,
∵周长为
∴DE+EF+DF=12
∴DF=12-DE-EF=3cm
故答案为:3
15.45°
【详解】解:∵△ABE≌△ACD,
∴∠AEB=∠ADE,
∵∠ADB=105°,
∴∠ADE=180°-105°=75°,
∴∠AEB=75°,
∵∠B=60°,
∴∠BAE=180°-60°-75°=45°.
故答案为45°.
16.20
【详解】∵△ABC≌△DCB,
∴∠D=∠A=80°,∠ACB=DBC=40°,
∴∠DCB=180°-∠D-∠DBC=60°,
∴∠DCA=∠DCB-∠ACB=20°,
故答案为20.
17.50
【详解】解:∵∠E=40°,∠C=25°,∠E+C+∠CAE=180°,
∴∠CAE=115°,
又∵△ADB≌△ACE,
∴∠DAB=∠CAE=115°,
∵∠BAE=180°,
∴∠DAC=∠DAB+∠C-180°=115°+115°-180°=50°.
故答案是:50°.
18.70
【详解】∵△ABC≌△ADE,
∴∠BAC=∠DAE,AB=AD,
∴∠BAD=∠EAC=40°,
∴∠B=(180°-40°)÷2=70°,
故答案为:70
19.(1);(2)
【详解】解:(1)∵
∴
由三角形外角的性质可得:
∠1的度数为
(2)∵
∴
∴
即AC的长为
20.(1)证明见解析;(2)∠EFC=60°.
【详解】(1)如图设DE交BC于点O.
由旋转的性质可知:△ABC≌△DBE(旋转不变性),
∴∠C=∠E.
(2)如图设DE交BC于点O.
∵∠C+∠COF+∠CFO=180°,∠E+∠EOB+∠OBE=180°,
又∵∠COF=∠EOB,∠OBE=60°,
∴∠CFO=∠OBE=60°,
即∠EFC=60°.
21.(1);(2)
【详解】(1)∵,
∴,,
∵点E在上,
∴,
∴;
(2)∵,
∴∠A=∠D=35,,
,
.
22.(1)其他对应角为和,和;其他对应边为和和;(2);(3).
【详解】(1)其他对应角为:和,和;
其他对应边为:和和;
(2)∵,
∴
∵,
∴;
(3)∵,
∴,
∴,
∴,
∴,
∴,
∴.
23.(1)90°
(2)8
【分析】(1)根据垂直的定义得到∠D=90°,求得∠DBA+∠BAD=90°,根据全等三角形的性质得到∠DBA=∠CAE,等量代换即可得到结论;
(2)根据全等三角形的性质得AC=AB=4,再根据三角形的面积求出答案.
(1)
解:∵BD⊥DE,
∴∠D=90°,
∴∠DBA+∠BAD=90°,
∵△ABD≌△CAE,
∴∠DBA=∠CAE
∴∠BAD+∠CAE=90°,
∴∠BAC=90°;
(2)
解:∵△ABD≌△CAE,
∴AC=AB=4,
又∵∠BAC=90°
∴△ABC是直角三角形,
∴△ABC的面积=4×4÷2=8.
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
一、单选题
1.如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=6cm,AD=5cm,那么BC的长是( )
A.4cm B.5cm C.6cm D.无法确定
2.如图,已知△ABC≌△EDF,下列结论正确的是( )
A.∠A=∠E B.∠B=∠DFE C.AC=ED D.BF=DF
3.如图,已知△ABE≌△ACD,下列选项中不能被证明的等式是( )
A.AD=AE B.DB=AE C.DF=EF D.DB=EC
4.全等图形是指两个图形( )
A.能够重合 B.形状相同 C.大小相同 D.相等
5.下列说法中正确的是( )
A.两个面积相等的图形,一定是全等图形
B.两个等边三角形是全等图形
C.两个全等图形的面积一定相等
D.若两个图形周长相等,则它们一定是全等图形
6.三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是( )
A. B. C. D.
7.如图,△ACF≌△BDE,点A、B、C、D在同一条直线上,下列结论中错误的是( )
A.AF∥BE B.∠ACF=∠DBE C.AB=CD D.CF∥DE
8.如图是两个全等三角形,图中的字母表示三角形的边长,则的度数是( )
A. B. C. D.
9.如图,,则的长是( )
A. B. C. D.
10.如图,△ABC≌△DEC,∠ACB=90°,∠DCB=20°,则∠BCE的度数为( )
A.20° B.40° C.70° D.90°
11.如图,△ABC≌△ADE,∠B=70°,∠C=26°,∠DAC=30°,则∠EAC=( )
A.27° B.30° C.54° D.55°
12.下图所示的图形分割成两个全等的图形,正确的是( )
A. B. C. D.
二、填空题
13.一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x + y =________.
14.已知,与,与是对应点,周长为,,,则________________.
15.如图,△ABE≌△ACD,∠ADB=105°,∠B=60°则∠BAE=________.
16.如图,△ABC≌△DCB.若A=80°,DBC=40°,则DCA的大小为____度.
17.如图,点B、A、E在同一直线上,△ADB≌△ACE,∠E=40°,∠C=25°,则∠DAC=______°.
18.如图,△ABC≌△ADE,∠EAC=40°,则∠B=_______°.
三、解答题
19.如图△ADF≌△BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm.求:
(1)∠1的度数;(2)AC的长.
20.如图,将△ABC绕点B顺时针旋转60°后得到△BDE(点A对应点为D),线段AC交线段DE于点F.
(1)求证:∠C=∠E;
(2)求EFC的度数.
21.如图,,点在上,与相交于点,若,,,.
(1)求线段的长;
(2)求的度数.
22.如图,和是对应角,和是对应边.
(1)写出和的其他对应角和对应边;
(2)若,求的度数;
(3)若,求的长.
23.如图,D、A、E三点在同一条直线上,BD⊥DE于点D,CE⊥DE于点E,且△ABD≌△CAE,AC=4.
(1)求∠BAC的度数;
(2)求△ABC的面积.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
1.B
【详解】解:∵△ABC≌△BAD,AB=6cm,BD=6cm,AD=5cm,
∴BC=AD=5cm.
故选:B.
2.A
【详解】解:∵△ABC≌△EDF,
∴∠A=∠E,A正确;
∠B=∠FDE,B错误;
AC=EF,C错误;
BF=DC,D错误;
故选A.
3.B
【详解】试题解析:∵△ABE≌△ACD,
∴AB=AC,AD=AE,∠B=∠C,故A正确;
∴AB-AD=AC-AE,即BD=EC,故D正确;
在△BDF和△CEF中
∴△BDF≌△CEF(ASA),
∴DF=EF,故C正确;
故选B.
4.A
【详解】解:根据全等图形的定义:能够重合的两个图形叫做全等图形,
故选:A.
5.C
【详解】解:A、两个面积相等的图形不一定是全等图形,故A错误;
B、两个等边三角形不一定是全等图形,故B错误;
C、两个全等图形的面积一定相等,正确;
D、若两个图形的周长相等,则它们不一定是全等形,故D错误;
故选:C.
6.D
【详解】∵图中是三个全等三角形,
∴∠4=∠8, ∠6=∠7,
又∵三角形ABC的外角和=∠1+∠2+∠3+∠4+∠5+∠6=360 ,
又∠5+∠7+∠8=180°,
∴∠1+∠2+∠3=360°-180°=180°.
故选D
7.B
【详解】解:∵△ACF≌△BDE,
∴∠A=∠EBD,
∴AF∥BE,A正确,不符合题意;
∴∠ACF=∠BDE,B错误,符合题意;
∴AC=BD,
∴AB=CD,C正确,不符合题意;
∴∠D=∠FCA,
∴CF∥DE,D正确,不符合题意;
故选B.
8.C
【详解】解:∵如图是两个全等三角形,
∴∠1=∠2=180°-48°-46°=86°.
故选:C.
9.D
【详解】解:∵△ABC≌△CDA,
∴AD=BC=8cm.
故选D.
10.C
【详解】解:∵△ABC≌△DEC,
∴∠DCE=∠ACB,
∴∠BCE=∠DCE﹣∠DCB=90°﹣20°=70°.
故选:C.
11.C
【详解】解:∵∠B=70°,∠C=26°,
∴∠BAC=180°-70°-26°=84°,
∵∠DAC=30°,
∴∠BAD=84°-30°=54°,
∵△ABC△ADE,
∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠EAC=∠BAD=54°,
故答案为C.
12.B
【详解】解:图形分割成两个全等的图形,如图所示:
故选B.
13.11
【详解】解:∵这两个三角形全等
∴x=6,y=5
∴x + y =11
故答案为11.
14.3
【详解】解:∵,,,
∴,
∵周长为
∴DE+EF+DF=12
∴DF=12-DE-EF=3cm
故答案为:3
15.45°
【详解】解:∵△ABE≌△ACD,
∴∠AEB=∠ADE,
∵∠ADB=105°,
∴∠ADE=180°-105°=75°,
∴∠AEB=75°,
∵∠B=60°,
∴∠BAE=180°-60°-75°=45°.
故答案为45°.
16.20
【详解】∵△ABC≌△DCB,
∴∠D=∠A=80°,∠ACB=DBC=40°,
∴∠DCB=180°-∠D-∠DBC=60°,
∴∠DCA=∠DCB-∠ACB=20°,
故答案为20.
17.50
【详解】解:∵∠E=40°,∠C=25°,∠E+C+∠CAE=180°,
∴∠CAE=115°,
又∵△ADB≌△ACE,
∴∠DAB=∠CAE=115°,
∵∠BAE=180°,
∴∠DAC=∠DAB+∠C-180°=115°+115°-180°=50°.
故答案是:50°.
18.70
【详解】∵△ABC≌△ADE,
∴∠BAC=∠DAE,AB=AD,
∴∠BAD=∠EAC=40°,
∴∠B=(180°-40°)÷2=70°,
故答案为:70
19.(1);(2)
【详解】解:(1)∵
∴
由三角形外角的性质可得:
∠1的度数为
(2)∵
∴
∴
即AC的长为
20.(1)证明见解析;(2)∠EFC=60°.
【详解】(1)如图设DE交BC于点O.
由旋转的性质可知:△ABC≌△DBE(旋转不变性),
∴∠C=∠E.
(2)如图设DE交BC于点O.
∵∠C+∠COF+∠CFO=180°,∠E+∠EOB+∠OBE=180°,
又∵∠COF=∠EOB,∠OBE=60°,
∴∠CFO=∠OBE=60°,
即∠EFC=60°.
21.(1);(2)
【详解】(1)∵,
∴,,
∵点E在上,
∴,
∴;
(2)∵,
∴∠A=∠D=35,,
,
.
22.(1)其他对应角为和,和;其他对应边为和和;(2);(3).
【详解】(1)其他对应角为:和,和;
其他对应边为:和和;
(2)∵,
∴
∵,
∴;
(3)∵,
∴,
∴,
∴,
∴,
∴,
∴.
23.(1)90°
(2)8
【分析】(1)根据垂直的定义得到∠D=90°,求得∠DBA+∠BAD=90°,根据全等三角形的性质得到∠DBA=∠CAE,等量代换即可得到结论;
(2)根据全等三角形的性质得AC=AB=4,再根据三角形的面积求出答案.
(1)
解:∵BD⊥DE,
∴∠D=90°,
∴∠DBA+∠BAD=90°,
∵△ABD≌△CAE,
∴∠DBA=∠CAE
∴∠BAD+∠CAE=90°,
∴∠BAC=90°;
(2)
解:∵△ABD≌△CAE,
∴AC=AB=4,
又∵∠BAC=90°
∴△ABC是直角三角形,
∴△ABC的面积=4×4÷2=8.
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
