23.3.3 相似三角形的性质课时练习(含答案)
文档属性
| 名称 | 23.3.3 相似三角形的性质课时练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 713.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-18 00:00:00 | ||
图片预览




文档简介
23.3.3相似三角形的性质(附解析)
一、单选题(共10个小题)
1.已知,若△ABC与△DEF的对应边之比为3∶4,则△ABC与△DEF的面积之比为 ( )
A.4∶3 B.3∶4 C.16∶9 D.9∶16
2.有一个直角三角形的边长分别为3,4,5,另一个与它相似的直角三角形的最小边长为7,则另一个直角三角形的周长是( )
A. B. C.21 D.28
3.如图,在△ABC中,DE∥BC,,则下列结论中正确的是( )
A. B. C. D.
4.如图,点为△ABC的重心,则的值是( ).
A. B. C. D.无法确定
5.如下图所示,在△ABC中,点D在线段AC上,且△ABC∽△ADB,则下列结论一定正确的是( )
A. B.
C. D.
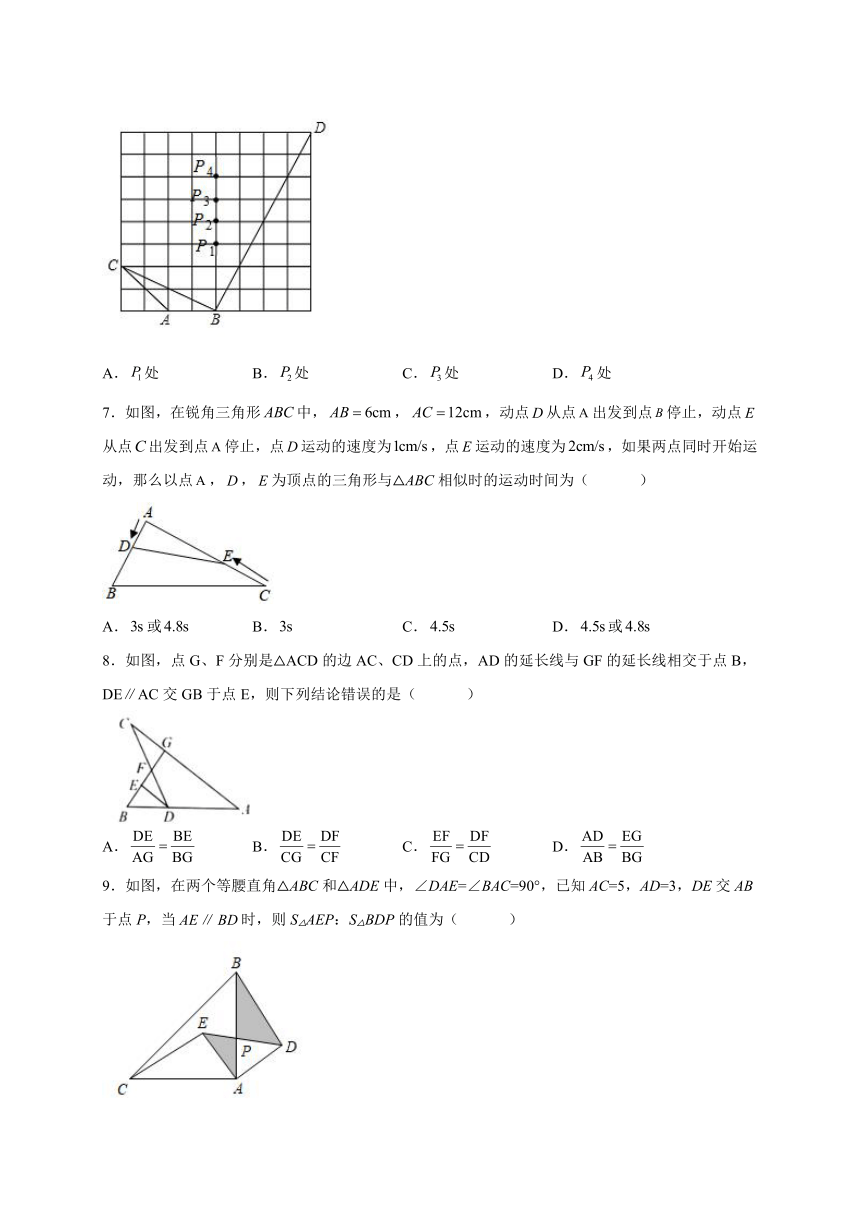
6.如图,在正方形网格上,若使△∽△,则点应在( )
A.处 B.处 C.处 D.处
7.如图,在锐角三角形中,,,动点从点出发到点停止,动点从点出发到点停止,点运动的速度为,点运动的速度为,如果两点同时开始运动,那么以点,,为顶点的三角形与△ABC相似时的运动时间为( )
A.或 B. C. D.或
8.如图,点G、F分别是△ACD的边AC、CD上的点,AD的延长线与GF的延长线相交于点B,DE∥AC交GB于点E,则下列结论错误的是( )
A. B. C. D.
9.如图,在两个等腰直角△ABC和△ADE中,∠DAE=∠BAC=90°,已知AC=5,AD=3,DE交AB于点P,当时,则S△AEP:S△BDP的值为( )
A. B. C. D.
10.如图,△OAB中,,,与轴相交于点,平分,点在双曲线上,点在双曲线上,则的值为( )
A. B. C. D.
二、填空题(共10个小题)
11.两个相似三角形的面积之比为3:4,则这两个三角形的周长之比为_______.
12.如图,在△ABC中,AB=9,AC=6,D为AB边上一点,且△ABC∽△ACD,则AD=__________.
13.如图,点E是平行四边形的边上的三等分点,连结交对角线于点F.若的面积为,则的面积是_________.
14.如图中,,,,点为上任意一点,连接,以,为邻边作平行四边形,连接,则的最小值为______.
15.已知点A(2,0),点B(b,0)(b>2),点P是第一象限内的动点,且点P的纵坐标为,若△POA和△PAB相似,则符合条件的点P坐标为_________.
16.如图,在平行四边形ABCD中,点E是AB的中点,CE和BD交于点O,若,则四边形AEOD的面积为___________.
17.如图,点是平行四边形的边的中点,,、相交于点,则________.
18.如图,点O是△ABC的重心,AD过点O交BC于D,BE是△ABD的中线,若△ABE的面积是2,则△ABC的面积是_______
19.如图,在△ABC中,,,点从点出发以1个单位/的速度向点运动,同时点从点出发以2个单位/的速度向点运动.当以,,为顶点的三角形与相似时,运动时间为______.
20.如图,要在底边,高的铁皮余料上,截取一个面积为的矩形EFGH,使点H在AB上,点G在AC上,点E,F在BC上,AD交HC于点M,则EH的长为_______cm.
三、解答题(共3个小题)
21.如图,已知是正方形的边上一点,于,求证:.
22.如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设点P、Q运动时间为t(s).
(1)当t为何值时,△PBQ的面积为9?
(2)当△PBQ与△ABC相似时,t的值是多少?
23.如图,在△ABC中,点D,F,E分别在AB,BC,AC边上,DFAC,EFAB.
(1)求证:△BDF∽△FEC.
(2)设.
①若BC=15,求线段BF的长;
②若△FEC的面积是16,求△ABC的面积.
23.3.3相似三角形的性质解析
1.
【答案】D
【详解】解:∵,△ABC与△DEF的对应边之比为3:4,
∴△ABC与△DEF的相似比为3:4,即△ABC与△DEF的面积之比为:9:16.
故选:D.
2.
【答案】D
【详解】解:设另一个直角三角形的周长为x,
∵三角形的边长分别为3,4,5,
∴周长为:3+4+5=12,
∵两个三角形相似,
∴,
解得:x=28,故D正确.
故选:D.
3.
【答案】C
【详解】解:∵DE∥BC,,
∴,△ADE∽△ABC,故B错误;
,故C正确;
,故D错误;
已有的条件不能说明,故A错误.
故选:C.
4.
【答案】C
【详解】解:如图所示,延长AG交BC于点D,
∵G点是三角形重心,
∴点D为△ABC的中点,
∴,
∵G点是三角形重心,
∴,
∴,
∴,
同理可证:,
∴,
故选:C.
5.
【答案】A
【详解】解:∵△ABC∽△ADB,
∴,
∴AB2=AC AD.
故选:A.
6.
【答案】B
【详解】解:由图知:∠BAC是钝角,又△ABC∽△PBD,
则∠BPD一定是钝角,∠BPD=∠BAC,
又BA=2,AC==2,BC==,,
∴,即,
∴BP=4,PD=4,
只有符合这样的要求,故P点应该在.
故选:B.
7.
【答案】A
【详解】解:设以点,,为顶点的三角形与相似时的运动时间为 ,
根据题意得: , ,则 ,
当 ,即 时,
∴,解得: ;
当 ,即 时,
∴,解得: ,
综上所述,以点 ,,为顶点的三角形与相似时的运动时间为或.
故选:A
8.
【答案】C
【详解】A选项正确:∵DE∥AC,
∴,
∴,
故A正确;
B选项正确:∵DE∥AC,
∴,
∴,
故B正确;
C选项错误:∵,
∴,
故C错误;
D选项正确:∵DE∥AC,
∴,
故D正确;
所以答案为:C.
9.
【答案】D
【详解】解:∵△ABC和△ADE都是等腰直角三角形,∠DAE=∠BAC=90°,
∴AB=AC=5,∠ADE=∠AED=45°,AE=AD=3,
∵,
∴△AEP∽△BDP,
∴,
∵
∴∠BDP=∠AED=45°,
∵∠ADB=90°,,
∴,
∴,
故选D.
10.
【答案】D
【详解】解:△OAB中,∠OAB=90°,∠OBA=30°,
∴∠AOB=60°,,
作AM⊥x轴于M,BN⊥x轴于N,
∵OC平分∠AOB,
∴∠AOC=∠BOC=30°,
∵∠AMO=∠BNO,
∴△AOM∽△BON,
∴,
∵,
∴,
∴,
∵k<0,
∴.
故选:D.
11.
【详解】解:∵两个相似三角形的面积之比为3:4,
∴相似比是:2,
∵相似三角形的周长比等于相似比,
∴这两个三角形的周长之比为::2,
故答案为::2.
12.
【答案】4.
【详解】∵△ABC∽△ACD,∴,
∵AB=9,AC=6,∴,解得:AD=4.
故答案为:4.
13.
【答案】2cm2.
【详解】解:∵四边形ABCD是平行四边形,
∴,AD=BC,
∴△AFD∽△EFB.
∵点E是平行四边形ABCD的边BC上的三等分点,
∴BC:BE=3:1,
∴AD:BE=3:1,
∴△AFD、△EFB的相似比为3:1,
∴,
∵△ADF的面积为18cm2,
∴△BEF的面积为2cm2.
故答案为:2cm2.
14.
【答案】
【详解】解:如图,设PQ,AC交于点D,过点D作DE⊥BC于点E,
∴∠CED=90°
∵四边形PAQC是平行四边形,
∴,,
当PD⊥BC时,PD取得最小值,即PQ最小,
∴当P、E重合时,PD最小,
∵∠BAC=90°,AB=3,AC=4,
∴∠CAB=∠CED,,
又∵∠DCE=∠BCA,
∴△CED∽△CAB,
∴,即,
∴,
∴.
故答案为:.
15.
【答案】
【详解】由题意可得:OA=2,OB=b,AP=,
如图:(1)当时,
,
OA=AB=2,
b=4,
P(2,);
(2)当时,
,
,
解得:b=9±,
P(2,3±);
综上:P的坐标为:(2,),(2,3±).
故答案为:(2,),(2,3±).
16.
【答案】5
【详解】解:∵在平行四边形ABCD中,点E是AB的中点,
∴CD∥AB,,
∴△DOC∽△BOE,
∴,
∴,
∴,
∴,,
∴,
∵四边形ABCD为平行四边形,
∴,
∴,
故答案为:5.
17.
【答案】1:7
【详解】如下图,延长EF,CD,相交于H点,
∵四边形ABCD是平行四边形
∴
∴∽,∽,
∵
∴
∵点E是AB的中点,
∴
∴
∴
∴
18.
【答案】8
【详解】解:∵BE是△ABD的中线,
∴,
∴,
∴,
∵点O是△ABC的重心,
∴是△ABC的中线,
∴,
∴,
∴,
即△ABC的面积是8.
故答案为:8.
19.
【答案】s或s
【详解】解:设运动时间为t,由题意可得:QC=2t,BQ=6-2t,BP=t,则有:
∵,,当以,,为顶点的三角形与相似时,
∴①当时,则有:
,解得:;
②当时,则有:
,解得:;
综上所述:当以,,为顶点的三角形与相似时,运动时间为s或s;
故答案为s或s.
20.
【答案】90或30
【详解】设,
∵矩形EFGH的面积为,∴.
∵,∴△AHG∽ △ABC.
又∵AM,AD分别为与的高,∴,
即,解得,,
∴EH的长为90cm或30cm.
21.
【答案】见解析
【详解】证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠D=90°,
∴∠BAF+∠DAE=90°,
∵,
∴∠AFB=∠D=90°,
∴∠BAF+∠ABF=90°,
∴∠DAE=∠BAF,
∴△ADE∽△BFA,
∴,
∴AD·AB=AE·BF,
∴.
22.
【答案】(1)3s;(2)或
【详解】(1)解:由题意得,,,则.
,
由题意得,
解得,
所以运动时间为;
(2)解:若当时,.
即,
解得;
当时,.
即,
解得.
综上所述,当与相似时,的值是或.
23.
【答案】(1)证明见详解;(2)①BF=5;②S△ABC=16×=36
【详解】(1)证明:∵DFAC,
∴∠BFD=∠C,
∵EFAB,
∴∠B=∠EFC,
∵∠BFD=∠C,∠B=∠EFC,
∴△BDF∽△FEC;
(2)解:①∵EFAB,
∴,
∴
∵BC=15,
∴,
∴BF=5;
②∵,
∴
∴,
∵EFAB,
∴∠CEF=∠B,
∵∠C=∠C.∠CEF=∠B
∴△EFC∽△ABC,
∴,
∵S△EFC=16,
∴S△ABC=×16=36.
一、单选题(共10个小题)
1.已知,若△ABC与△DEF的对应边之比为3∶4,则△ABC与△DEF的面积之比为 ( )
A.4∶3 B.3∶4 C.16∶9 D.9∶16
2.有一个直角三角形的边长分别为3,4,5,另一个与它相似的直角三角形的最小边长为7,则另一个直角三角形的周长是( )
A. B. C.21 D.28
3.如图,在△ABC中,DE∥BC,,则下列结论中正确的是( )
A. B. C. D.
4.如图,点为△ABC的重心,则的值是( ).
A. B. C. D.无法确定
5.如下图所示,在△ABC中,点D在线段AC上,且△ABC∽△ADB,则下列结论一定正确的是( )
A. B.
C. D.
6.如图,在正方形网格上,若使△∽△,则点应在( )
A.处 B.处 C.处 D.处
7.如图,在锐角三角形中,,,动点从点出发到点停止,动点从点出发到点停止,点运动的速度为,点运动的速度为,如果两点同时开始运动,那么以点,,为顶点的三角形与△ABC相似时的运动时间为( )
A.或 B. C. D.或
8.如图,点G、F分别是△ACD的边AC、CD上的点,AD的延长线与GF的延长线相交于点B,DE∥AC交GB于点E,则下列结论错误的是( )
A. B. C. D.
9.如图,在两个等腰直角△ABC和△ADE中,∠DAE=∠BAC=90°,已知AC=5,AD=3,DE交AB于点P,当时,则S△AEP:S△BDP的值为( )
A. B. C. D.
10.如图,△OAB中,,,与轴相交于点,平分,点在双曲线上,点在双曲线上,则的值为( )
A. B. C. D.
二、填空题(共10个小题)
11.两个相似三角形的面积之比为3:4,则这两个三角形的周长之比为_______.
12.如图,在△ABC中,AB=9,AC=6,D为AB边上一点,且△ABC∽△ACD,则AD=__________.
13.如图,点E是平行四边形的边上的三等分点,连结交对角线于点F.若的面积为,则的面积是_________.
14.如图中,,,,点为上任意一点,连接,以,为邻边作平行四边形,连接,则的最小值为______.
15.已知点A(2,0),点B(b,0)(b>2),点P是第一象限内的动点,且点P的纵坐标为,若△POA和△PAB相似,则符合条件的点P坐标为_________.
16.如图,在平行四边形ABCD中,点E是AB的中点,CE和BD交于点O,若,则四边形AEOD的面积为___________.
17.如图,点是平行四边形的边的中点,,、相交于点,则________.
18.如图,点O是△ABC的重心,AD过点O交BC于D,BE是△ABD的中线,若△ABE的面积是2,则△ABC的面积是_______
19.如图,在△ABC中,,,点从点出发以1个单位/的速度向点运动,同时点从点出发以2个单位/的速度向点运动.当以,,为顶点的三角形与相似时,运动时间为______.
20.如图,要在底边,高的铁皮余料上,截取一个面积为的矩形EFGH,使点H在AB上,点G在AC上,点E,F在BC上,AD交HC于点M,则EH的长为_______cm.
三、解答题(共3个小题)
21.如图,已知是正方形的边上一点,于,求证:.
22.如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设点P、Q运动时间为t(s).
(1)当t为何值时,△PBQ的面积为9?
(2)当△PBQ与△ABC相似时,t的值是多少?
23.如图,在△ABC中,点D,F,E分别在AB,BC,AC边上,DFAC,EFAB.
(1)求证:△BDF∽△FEC.
(2)设.
①若BC=15,求线段BF的长;
②若△FEC的面积是16,求△ABC的面积.
23.3.3相似三角形的性质解析
1.
【答案】D
【详解】解:∵,△ABC与△DEF的对应边之比为3:4,
∴△ABC与△DEF的相似比为3:4,即△ABC与△DEF的面积之比为:9:16.
故选:D.
2.
【答案】D
【详解】解:设另一个直角三角形的周长为x,
∵三角形的边长分别为3,4,5,
∴周长为:3+4+5=12,
∵两个三角形相似,
∴,
解得:x=28,故D正确.
故选:D.
3.
【答案】C
【详解】解:∵DE∥BC,,
∴,△ADE∽△ABC,故B错误;
,故C正确;
,故D错误;
已有的条件不能说明,故A错误.
故选:C.
4.
【答案】C
【详解】解:如图所示,延长AG交BC于点D,
∵G点是三角形重心,
∴点D为△ABC的中点,
∴,
∵G点是三角形重心,
∴,
∴,
∴,
同理可证:,
∴,
故选:C.
5.
【答案】A
【详解】解:∵△ABC∽△ADB,
∴,
∴AB2=AC AD.
故选:A.
6.
【答案】B
【详解】解:由图知:∠BAC是钝角,又△ABC∽△PBD,
则∠BPD一定是钝角,∠BPD=∠BAC,
又BA=2,AC==2,BC==,,
∴,即,
∴BP=4,PD=4,
只有符合这样的要求,故P点应该在.
故选:B.
7.
【答案】A
【详解】解:设以点,,为顶点的三角形与相似时的运动时间为 ,
根据题意得: , ,则 ,
当 ,即 时,
∴,解得: ;
当 ,即 时,
∴,解得: ,
综上所述,以点 ,,为顶点的三角形与相似时的运动时间为或.
故选:A
8.
【答案】C
【详解】A选项正确:∵DE∥AC,
∴,
∴,
故A正确;
B选项正确:∵DE∥AC,
∴,
∴,
故B正确;
C选项错误:∵,
∴,
故C错误;
D选项正确:∵DE∥AC,
∴,
故D正确;
所以答案为:C.
9.
【答案】D
【详解】解:∵△ABC和△ADE都是等腰直角三角形,∠DAE=∠BAC=90°,
∴AB=AC=5,∠ADE=∠AED=45°,AE=AD=3,
∵,
∴△AEP∽△BDP,
∴,
∵
∴∠BDP=∠AED=45°,
∵∠ADB=90°,,
∴,
∴,
故选D.
10.
【答案】D
【详解】解:△OAB中,∠OAB=90°,∠OBA=30°,
∴∠AOB=60°,,
作AM⊥x轴于M,BN⊥x轴于N,
∵OC平分∠AOB,
∴∠AOC=∠BOC=30°,
∵∠AMO=∠BNO,
∴△AOM∽△BON,
∴,
∵,
∴,
∴,
∵k<0,
∴.
故选:D.
11.
【详解】解:∵两个相似三角形的面积之比为3:4,
∴相似比是:2,
∵相似三角形的周长比等于相似比,
∴这两个三角形的周长之比为::2,
故答案为::2.
12.
【答案】4.
【详解】∵△ABC∽△ACD,∴,
∵AB=9,AC=6,∴,解得:AD=4.
故答案为:4.
13.
【答案】2cm2.
【详解】解:∵四边形ABCD是平行四边形,
∴,AD=BC,
∴△AFD∽△EFB.
∵点E是平行四边形ABCD的边BC上的三等分点,
∴BC:BE=3:1,
∴AD:BE=3:1,
∴△AFD、△EFB的相似比为3:1,
∴,
∵△ADF的面积为18cm2,
∴△BEF的面积为2cm2.
故答案为:2cm2.
14.
【答案】
【详解】解:如图,设PQ,AC交于点D,过点D作DE⊥BC于点E,
∴∠CED=90°
∵四边形PAQC是平行四边形,
∴,,
当PD⊥BC时,PD取得最小值,即PQ最小,
∴当P、E重合时,PD最小,
∵∠BAC=90°,AB=3,AC=4,
∴∠CAB=∠CED,,
又∵∠DCE=∠BCA,
∴△CED∽△CAB,
∴,即,
∴,
∴.
故答案为:.
15.
【答案】
【详解】由题意可得:OA=2,OB=b,AP=,
如图:(1)当时,
,
OA=AB=2,
b=4,
P(2,);
(2)当时,
,
,
解得:b=9±,
P(2,3±);
综上:P的坐标为:(2,),(2,3±).
故答案为:(2,),(2,3±).
16.
【答案】5
【详解】解:∵在平行四边形ABCD中,点E是AB的中点,
∴CD∥AB,,
∴△DOC∽△BOE,
∴,
∴,
∴,
∴,,
∴,
∵四边形ABCD为平行四边形,
∴,
∴,
故答案为:5.
17.
【答案】1:7
【详解】如下图,延长EF,CD,相交于H点,
∵四边形ABCD是平行四边形
∴
∴∽,∽,
∵
∴
∵点E是AB的中点,
∴
∴
∴
∴
18.
【答案】8
【详解】解:∵BE是△ABD的中线,
∴,
∴,
∴,
∵点O是△ABC的重心,
∴是△ABC的中线,
∴,
∴,
∴,
即△ABC的面积是8.
故答案为:8.
19.
【答案】s或s
【详解】解:设运动时间为t,由题意可得:QC=2t,BQ=6-2t,BP=t,则有:
∵,,当以,,为顶点的三角形与相似时,
∴①当时,则有:
,解得:;
②当时,则有:
,解得:;
综上所述:当以,,为顶点的三角形与相似时,运动时间为s或s;
故答案为s或s.
20.
【答案】90或30
【详解】设,
∵矩形EFGH的面积为,∴.
∵,∴△AHG∽ △ABC.
又∵AM,AD分别为与的高,∴,
即,解得,,
∴EH的长为90cm或30cm.
21.
【答案】见解析
【详解】证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠D=90°,
∴∠BAF+∠DAE=90°,
∵,
∴∠AFB=∠D=90°,
∴∠BAF+∠ABF=90°,
∴∠DAE=∠BAF,
∴△ADE∽△BFA,
∴,
∴AD·AB=AE·BF,
∴.
22.
【答案】(1)3s;(2)或
【详解】(1)解:由题意得,,,则.
,
由题意得,
解得,
所以运动时间为;
(2)解:若当时,.
即,
解得;
当时,.
即,
解得.
综上所述,当与相似时,的值是或.
23.
【答案】(1)证明见详解;(2)①BF=5;②S△ABC=16×=36
【详解】(1)证明:∵DFAC,
∴∠BFD=∠C,
∵EFAB,
∴∠B=∠EFC,
∵∠BFD=∠C,∠B=∠EFC,
∴△BDF∽△FEC;
(2)解:①∵EFAB,
∴,
∴
∵BC=15,
∴,
∴BF=5;
②∵,
∴
∴,
∵EFAB,
∴∠CEF=∠B,
∵∠C=∠C.∠CEF=∠B
∴△EFC∽△ABC,
∴,
∵S△EFC=16,
∴S△ABC=×16=36.
