人教A版(2019)高中数学必修第一册 3.2 函数的基本性质 课件(共33张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第一册 3.2 函数的基本性质 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 07:17:32 | ||
图片预览










文档简介
(共33张PPT)
3.2 函数的基本性质
第三章 函数的概念与性质
目录
二、知识讲解
三、小结
四、练习
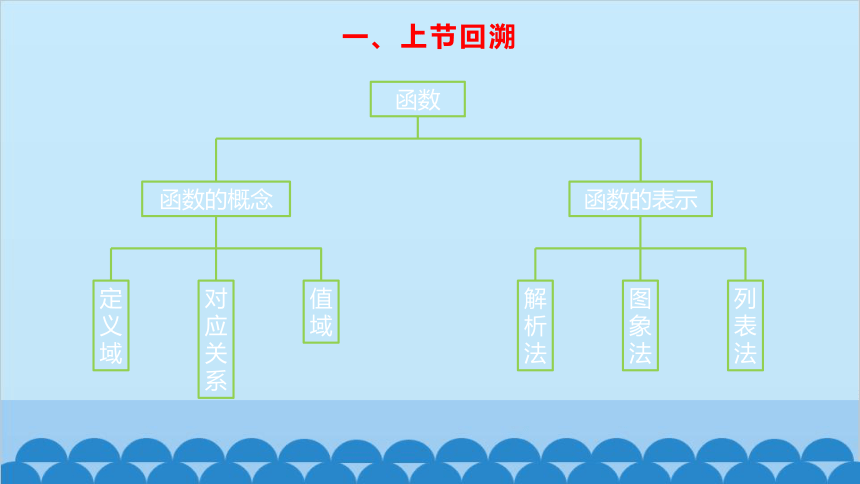
一、上节回溯
一、上节回溯
对应关系
定义域
函数的表示
值域
函数
函数的概念
图象法
解析法
列表法
二、知识讲解
前面学习了函数的定义和表示法,知道函数 y=f (x)(x∈A) 描述了客观世界中变量之间的一种对应关系.这样,我们就可以通过研究函数的变化规律来把握客观世界中事物的变化规律.因此,研究函数的性质,如随着自变量的增大函数值是增大还是减小,有没有最大值或最小值,函数图象有什么特征等,是认识客观规律的重要方法.
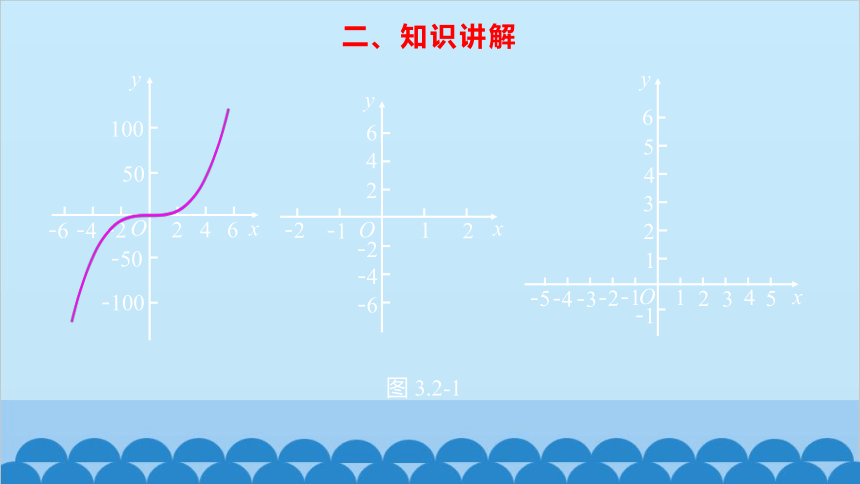
我们知道,先画出函数图象,通过观察和分析图象的特征,可以得到函数的一些性质.观察图 3.2-1 中的各个函数图象,你能说说它们分别反映了相应函数的哪些性质吗?
二、知识讲解
图 3.2-1
y
x
O
2
4
6
-4
-2
50
100
-50
-100
-6
y
x
O
1
2
6
-2
-1
2
4
-2
-4
-6
y
x
O
1
2
3
-2
-1
1
2
3
4
5
-3
4
5
-4
-5
-1
6
3.2.1 单调性与最大(小)值
二、知识讲解
在初中,我们利用函数图象研究过函数值随自变量的增大而增大(或减小)的性质,这一性质叫做函数的单调性.下面进一步用符号语言刻画这种性质.
先研究二次函数 f (x)=x2 的单调性.
画出它的图象(如图 3.2-2),可以看到:
y
x
O
f (x2)
x1
x2
图 3.2-2
f (x1)
f (x)=x2
二、知识讲解
y
x
O
f (x2)
x1
x2
图 3.2-2
f (x1)
f (x)=x2
你能说明为什么 f (x1)>f (x2) 吗?
?
你能说明为什么 f (x1)?
二、知识讲解
函数 f (x)=|x|,f (x)=-x2 各有怎样的单调性?
?
思考
y
x
O
f (x2)
x1
x2
f (x1)
y=f (x)
二、知识讲解
y
x
O
f (x2)
x1
x2
f (x1)
y=f (x)
二、知识讲解
?
思考
二、知识讲解
例1 根据定义,研究函数 f (x)=kx+b (k≠0) 的单调性.
分析:根据函数单调性的定义,需要考察当 x1 f (x2).根据实数大小关系的基本事实,只要考察 f (x1)-f (x2) 与 0 的大小关系.
二、知识讲解
二、知识讲解
y
x
O
f (x2)
x1
x2
图 3.2-2
f (x1)
f (x)=x2
你能以函数 f (x)=-x2 为例说明函数 f (x) 的最大值的含义吗?
?
思考
二、知识讲解
你能仿照函数最大值的定义,给出函数 y=f (x) 的最小值(minimum value)的定义吗?
?
思考
二、知识讲解
例4 “菊花”烟花是最壮观的烟花之一.制造时一般是期望在它达到最高点时爆裂.如果烟花距地面的高度 h(单位:m)与时间 t(单位:s)之间的关系为 h(t)=-4.9t2+14.7t+18,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到 1 m)?
解:画出函数 h(t)=-4.9t2+14.7t+18 的图象(图 3.2-4).显然,函数图象的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度.
二、知识讲解
h
t
O
1
2
3
2.5
1.5
5
10
15
25
20
3.5
4
图 3.2-4
0.5
30
二、知识讲解
y
x
O
1
2
3
4
5
0.5
1
1.5
2.5
2
图 3.2-5
6
3.2.2 奇偶性
二、知识讲解
前面我们用符号语言精确地描述了函数图象在定义域的某个区间上“上升”(或“下降”)的性质.下面继续研究函数的其他性质.
画出并观察函数 f (x)=x2 和 g (x)=2-|x| 的图象(图 3.2-6),你能发现这两个函数图象有什么共同特征吗?
可以发现,这两个函数的图象都关于 y 轴对称.
y
x
O
1
2
3
-2
-1
1
2
3
4
5
-3
g (x)=2-|x|
y
x
O
1
2
3
-2
-1
1
2
3
4
5
-3
f (x)=x2
图 3.2-6
二、知识讲解
不妨取自变量的一些特殊值,观察相应函数值的情况,如表 3.2-1.
可以发现,当自变量取一对相反数时,相应的两个函数值相等.
类比函数单调性,你能用符号语言精确地描述“函数图象关于 y 轴对称”这一特征吗?
探究
表 3.2-1
x
f (x)=x2
g (x)=2-|x|
…
…
…
…
…
…
-2
-3
3
2
9
1
0
-1
-1
-1
0
1
4
0
0
1
1
1
2
4
9
二、知识讲解
二、知识讲解
图 3.2-7
y
x
O
1
2
3
-2
-1
1
2
3
4
5
-3
f (x)=x2+1
(1)
y
x
O
1
2
3
-2
-1
0.10
0.20
-4
4
5
-3
-5
(2)
二、知识讲解
探究
y
x
O
1
2
3
-2
-1
1
2
3
-1
-2
-3
f (x)=x
-3
y
x
O
1
2
3
-2
-1
1
2
3
-1
-2
-3
-3
图 3.2-8
二、知识讲解
可以发现,两个函数的图象都关于原点成中心对称图形.为了用符号语言描述这一特征,不妨取自变量的一些特殊值,看相应函数值的情况,请完成表 3.2-2.
可以发现,当自变量 x 取一对相反数时,相应的函数值 f (x) 也是一对相反数.
表 3.2-2
x
f (x)=x2
…
…
…
…
…
…
-2
-3
3
2
-1
0
1
二、知识讲解
二、知识讲解
二、知识讲解
二、知识讲解
(1)判断函数 f (x)=x3+x 的奇偶性.
(2)图 3.2-9 是函数 f (x)=x3+x 图象的一部分,你能根据 f (x) 的奇偶性画出它在 y 轴左边的图象吗?
(3)一般地,如果知道 y=f (x) 为偶(奇)函数,那么我们可以怎样简化对它的研究?
?
思考
y
x
O
1
2
3
-2
-1
1
2
3
-1
-2
-3
图 3.2-9
-3
-4
-5
4
5
三、小结
定义
奇偶性
图象特征
函数的基本性质
单调性与最大(小)值
定义
图象特征
1.请根据下图描述某装配线的生产效率与生产线上工人数量间的关系.
答案:在一定范围内,生产效率随着工人数的增加而提高,当工人数达到某个数量时,生产效率达到最大值,而超过这个数量时,生产效率又随着工人数的增加而降低.由此可见,并非是工人越多,生产效率越高.
四、练习
生产效率
工人数
O
四、练习
3.设函数 f (x) 的定义域为 [-6,11].如果 f (x) 在区间 [-6,-2] 上单调递减,在区间 [-2,11] 上单调递增,画出 f (x) 的一个大致的图象,从图象上可以发现 f (-2) 是函数 f (x) 的一个__________.
答案:最小值.
四、练习
5.判断下列函数的奇偶性:
(1)f (x)=2x4+3x2;
(2)f (x)=x3-2x.
答案:(1)偶函数.(2)奇函数.
四、练习
谢谢观看
3.2 函数的基本性质
第三章 函数的概念与性质
目录
二、知识讲解
三、小结
四、练习
一、上节回溯
一、上节回溯
对应关系
定义域
函数的表示
值域
函数
函数的概念
图象法
解析法
列表法
二、知识讲解
前面学习了函数的定义和表示法,知道函数 y=f (x)(x∈A) 描述了客观世界中变量之间的一种对应关系.这样,我们就可以通过研究函数的变化规律来把握客观世界中事物的变化规律.因此,研究函数的性质,如随着自变量的增大函数值是增大还是减小,有没有最大值或最小值,函数图象有什么特征等,是认识客观规律的重要方法.
我们知道,先画出函数图象,通过观察和分析图象的特征,可以得到函数的一些性质.观察图 3.2-1 中的各个函数图象,你能说说它们分别反映了相应函数的哪些性质吗?
二、知识讲解
图 3.2-1
y
x
O
2
4
6
-4
-2
50
100
-50
-100
-6
y
x
O
1
2
6
-2
-1
2
4
-2
-4
-6
y
x
O
1
2
3
-2
-1
1
2
3
4
5
-3
4
5
-4
-5
-1
6
3.2.1 单调性与最大(小)值
二、知识讲解
在初中,我们利用函数图象研究过函数值随自变量的增大而增大(或减小)的性质,这一性质叫做函数的单调性.下面进一步用符号语言刻画这种性质.
先研究二次函数 f (x)=x2 的单调性.
画出它的图象(如图 3.2-2),可以看到:
y
x
O
f (x2)
x1
x2
图 3.2-2
f (x1)
f (x)=x2
二、知识讲解
y
x
O
f (x2)
x1
x2
图 3.2-2
f (x1)
f (x)=x2
你能说明为什么 f (x1)>f (x2) 吗?
?
你能说明为什么 f (x1)
二、知识讲解
函数 f (x)=|x|,f (x)=-x2 各有怎样的单调性?
?
思考
y
x
O
f (x2)
x1
x2
f (x1)
y=f (x)
二、知识讲解
y
x
O
f (x2)
x1
x2
f (x1)
y=f (x)
二、知识讲解
?
思考
二、知识讲解
例1 根据定义,研究函数 f (x)=kx+b (k≠0) 的单调性.
分析:根据函数单调性的定义,需要考察当 x1
二、知识讲解
二、知识讲解
y
x
O
f (x2)
x1
x2
图 3.2-2
f (x1)
f (x)=x2
你能以函数 f (x)=-x2 为例说明函数 f (x) 的最大值的含义吗?
?
思考
二、知识讲解
你能仿照函数最大值的定义,给出函数 y=f (x) 的最小值(minimum value)的定义吗?
?
思考
二、知识讲解
例4 “菊花”烟花是最壮观的烟花之一.制造时一般是期望在它达到最高点时爆裂.如果烟花距地面的高度 h(单位:m)与时间 t(单位:s)之间的关系为 h(t)=-4.9t2+14.7t+18,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到 1 m)?
解:画出函数 h(t)=-4.9t2+14.7t+18 的图象(图 3.2-4).显然,函数图象的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度.
二、知识讲解
h
t
O
1
2
3
2.5
1.5
5
10
15
25
20
3.5
4
图 3.2-4
0.5
30
二、知识讲解
y
x
O
1
2
3
4
5
0.5
1
1.5
2.5
2
图 3.2-5
6
3.2.2 奇偶性
二、知识讲解
前面我们用符号语言精确地描述了函数图象在定义域的某个区间上“上升”(或“下降”)的性质.下面继续研究函数的其他性质.
画出并观察函数 f (x)=x2 和 g (x)=2-|x| 的图象(图 3.2-6),你能发现这两个函数图象有什么共同特征吗?
可以发现,这两个函数的图象都关于 y 轴对称.
y
x
O
1
2
3
-2
-1
1
2
3
4
5
-3
g (x)=2-|x|
y
x
O
1
2
3
-2
-1
1
2
3
4
5
-3
f (x)=x2
图 3.2-6
二、知识讲解
不妨取自变量的一些特殊值,观察相应函数值的情况,如表 3.2-1.
可以发现,当自变量取一对相反数时,相应的两个函数值相等.
类比函数单调性,你能用符号语言精确地描述“函数图象关于 y 轴对称”这一特征吗?
探究
表 3.2-1
x
f (x)=x2
g (x)=2-|x|
…
…
…
…
…
…
-2
-3
3
2
9
1
0
-1
-1
-1
0
1
4
0
0
1
1
1
2
4
9
二、知识讲解
二、知识讲解
图 3.2-7
y
x
O
1
2
3
-2
-1
1
2
3
4
5
-3
f (x)=x2+1
(1)
y
x
O
1
2
3
-2
-1
0.10
0.20
-4
4
5
-3
-5
(2)
二、知识讲解
探究
y
x
O
1
2
3
-2
-1
1
2
3
-1
-2
-3
f (x)=x
-3
y
x
O
1
2
3
-2
-1
1
2
3
-1
-2
-3
-3
图 3.2-8
二、知识讲解
可以发现,两个函数的图象都关于原点成中心对称图形.为了用符号语言描述这一特征,不妨取自变量的一些特殊值,看相应函数值的情况,请完成表 3.2-2.
可以发现,当自变量 x 取一对相反数时,相应的函数值 f (x) 也是一对相反数.
表 3.2-2
x
f (x)=x2
…
…
…
…
…
…
-2
-3
3
2
-1
0
1
二、知识讲解
二、知识讲解
二、知识讲解
二、知识讲解
(1)判断函数 f (x)=x3+x 的奇偶性.
(2)图 3.2-9 是函数 f (x)=x3+x 图象的一部分,你能根据 f (x) 的奇偶性画出它在 y 轴左边的图象吗?
(3)一般地,如果知道 y=f (x) 为偶(奇)函数,那么我们可以怎样简化对它的研究?
?
思考
y
x
O
1
2
3
-2
-1
1
2
3
-1
-2
-3
图 3.2-9
-3
-4
-5
4
5
三、小结
定义
奇偶性
图象特征
函数的基本性质
单调性与最大(小)值
定义
图象特征
1.请根据下图描述某装配线的生产效率与生产线上工人数量间的关系.
答案:在一定范围内,生产效率随着工人数的增加而提高,当工人数达到某个数量时,生产效率达到最大值,而超过这个数量时,生产效率又随着工人数的增加而降低.由此可见,并非是工人越多,生产效率越高.
四、练习
生产效率
工人数
O
四、练习
3.设函数 f (x) 的定义域为 [-6,11].如果 f (x) 在区间 [-6,-2] 上单调递减,在区间 [-2,11] 上单调递增,画出 f (x) 的一个大致的图象,从图象上可以发现 f (-2) 是函数 f (x) 的一个__________.
答案:最小值.
四、练习
5.判断下列函数的奇偶性:
(1)f (x)=2x4+3x2;
(2)f (x)=x3-2x.
答案:(1)偶函数.(2)奇函数.
四、练习
谢谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
