北师大版九年级数学上册 1.1菱形的性质与判定常考易错习题检测(含答案)
文档属性
| 名称 | 北师大版九年级数学上册 1.1菱形的性质与判定常考易错习题检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 695.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 08:05:47 | ||
图片预览

文档简介
2022-2023北师大版九年级数学上册第一章第一节
菱形的性质与判定 常考易错习题检测 (附带答案)
一.选择题(共10小题)
1.菱形具有而一般平行四边形不具有的性质是( )
A.对边平行 B.对边相等
C.对角线互相平分 D.对角线互相垂直
2.如图,菱形ABCD中,∠ABD=70°,则∠C的度数为( )
A.30° B.40° C.50° D.60°
3.菱形ABCD中,AC=10,BD=24,则该菱形的面积等于( )
A.13 B.52 C.120 D.240
4.如图,在菱形ABCD中,对角线AC,BD分别为16和12,DE⊥AB于点E,则DE=( )
A. B. C.10 D.8
5.如图, ABCD对角线AC,BD交于点O,请添加一个条件:____使得 ABCD是菱形( )
A.AB=AC B.AC⊥BD C.AB=CD D.AC=BD
6.如图,在菱形ABCD中,∠C=110°,BC的垂直平分线交BD于点E,F为垂足,连接AE,则∠EAD的度数是( )
A.60° B.65° C.70° D.75°
7. ABCD的对角线AC与BD相交于点O,添加以下条件,不能判定平行四边形ABCD为菱形的是( )
A.AC=BD B.AC⊥BD C.∠ACD=∠ACB D.BC=CD
8.如图,菱形ABCD对角线交点与坐标原点O重合,点A(﹣2,5),则点C的坐标是( )
A.(5,﹣2) B.(2,﹣5) C.(2,5) D.(﹣2,﹣5)
9.如图,在菱形ABCD中,顶点A,B,C,D在坐标轴上,且A(0,1),∠ABC=60°,分别以点A,D为圆心,以AD的长为半径作弧,两弧交于点E,连接EA,ED.将菱形ABCD与△EAD构成的图形绕点O逆时针旋转,每次旋转45°,则第2022次旋转结束时,点E2022的坐标为( )
A. B. C. D.
10.问题:已知:如图,四边形ABCD是菱形,E、F是直线AC上两点,AF=CE.求证:四边形FBED是菱形.
几名同学对这个问题,给出了如下几种解题思路,其中正确的是( )
甲:利用全等,证明四边形FBED四条边相等,进而说明该四边形是菱形;
乙:连接BD,利用对角线互相垂直的平行四边形是菱形,判定四边形FBED是菱形;
丙:该题目错误,根据已知条件不能够证明该四边形是菱形.
A.甲、乙对,丙错 B.乙、丙对,甲错
C.三个人都对 D.甲、丙对,乙错
二.填空题(共5小题)
11.如图,四边形ABCD是边长为cm的菱形,其中对角线BD的长为2cm,则菱形ABCD的面积为 cm2.
12.如图,已知点A的坐标是,2),点B的坐标是(﹣1,,菱形ABCD的对角线交于坐标原点O,则点D的坐标是 .
13.如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AH⊥BC于点H,连接OH,若OB=6,菱形ABCD的面积为48,则OH的长为 .
14.在菱形ABCD中,∠D=60°,CD=4,E为菱形内部一点,且AE=2,连接CE,点F为CE中点,连接BF,取BF中点G,连接AG,则AG的最大值为 .
15.如图,△ABC是边长为1的等边三角形,D,E为线段AC上两动点,且∠DBE=30°,过点D,E分别作AB,BC的平行线相交于点F,分别交BC,AB于点H,G.现有以下结论:①S△ABC=;②当点D与点C重合时,FH=;③AE+CD=DE;④当AE=CD时,四边形BHFG为菱形.则其中正确的结论的序号是 .
三.解答题(共5小题)
16.小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD交于点O,AC⊥BD,OB=OD.求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.
小惠: 证明:∵AC⊥BD,OB=OD, ∴AC垂直平分BD. ∴AB=AD,CB=CD, ∴四边形ABCD是菱形. 小洁: 这个题目还缺少条件,需要补充一个条件才能证明.
若赞同小惠的证法,请在第一个方框内打“√”;若赞成小洁的说法,请你补充一个条件,并证明.
17.如图,△ABC中,D,E分别是AC,AB的中点,DE=CE,过点B作BF∥CE,交DE的延长线于点F.
(1)求证:四边形BCEF是菱形.
(2)若BC=2,∠BCE=60°,求菱形BCEF的面积.
18.如图,四边形ABCD是菱形,E是AB的中点,AC的垂线EF交AD于点M,交CD的延长线于点F.
(1)求证:AM=AE;
(2)连接CM,DF=2.
①求菱形ABCD的周长;
②若∠ADC=2∠MCF,求ME的长.
19.如图,在平行四边形ABCD中,BE⊥AD,BF⊥CD,垂足分别为E,F,且AE=CF.
(1)求证:平行四边形ABCD是菱形;
(2)若DB=10,AB=13,求平行四边形ABCD的面积.
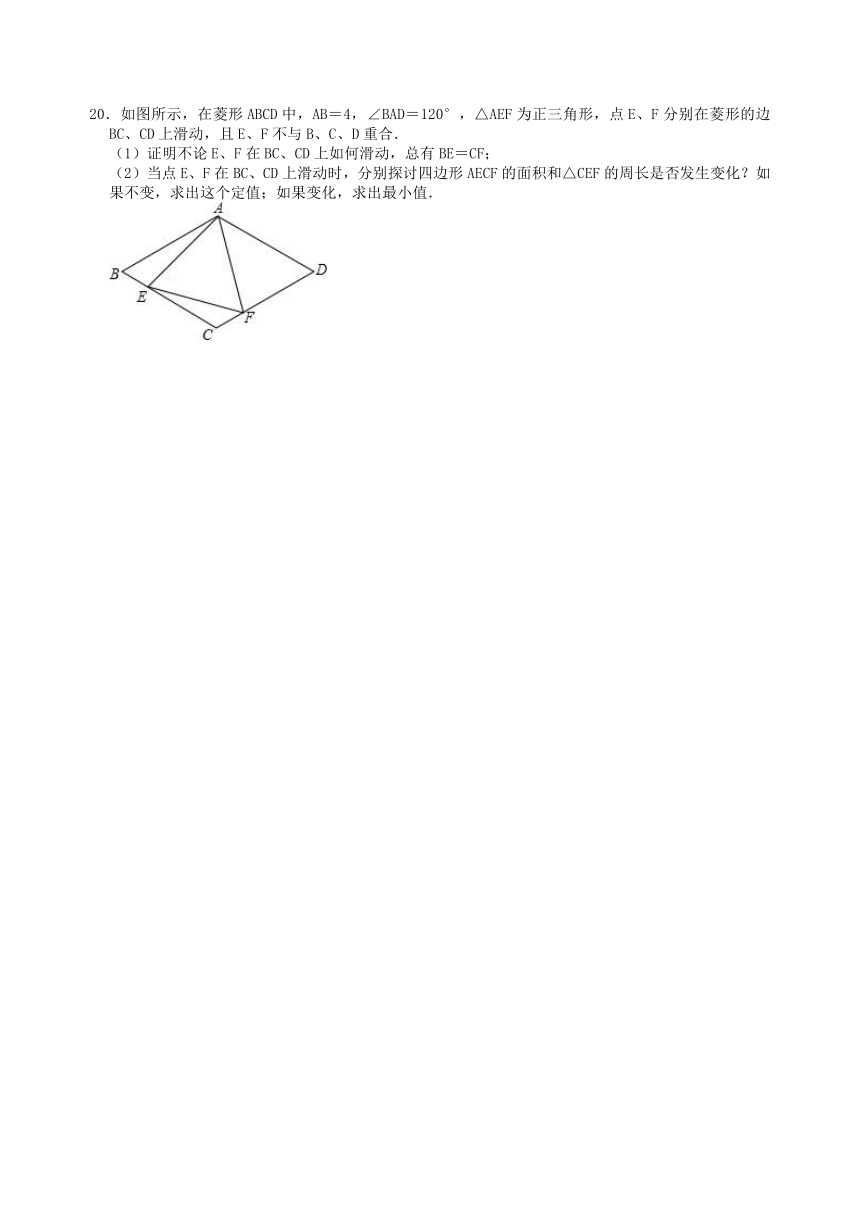
20.如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
(1)证明不论E、F在BC、CD上如何滑动,总有BE=CF;
(2)当点E、F在BC、CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:A.对边平行是菱形和一般平行四边形都具有的性质,故A不符合题意;
B.对边相等是菱形和一般平行四边形都具有的性质,故B不符合题意;
C.对角线互相平分是菱形和一般平行四边形都具有的性质,故C不符合题意;
D.对角线互相垂直是菱形具有而一般平行四边形不具有的性质,故D符合题意;
故选:D.
2.【解答】解:∵四边形ABCD是菱形,
∴∠ADC=∠ABC,DB平分∠ADC和∠ABC,
∴∠CDB=∠CBD=∠ADB=∠ABD=70°,
∴∠C=180°﹣2∠CDB=180°﹣2×70°=40°,
故选:B.
3.【解答】解:∵菱形对角线相互垂直,
∴AC⊥BD,
∴菱形面积是S=AC×BD==120.
故选:C.
4.【解答】解:如图,设AC与BD的交点为O,
∵四边形ABCD是菱形,
∴AO=CO=8,DO=BO=6,AC⊥BD,
∴AB===10,
∵S菱形ABCD=×AC×BD=AB×DE,
∴×16×12=10×DE,
∴DE=,
故选:A.
5.【解答】解:当AC⊥BD时, ABCD是菱形,
故选:B.
6.【解答】解:连接EC,AC,
∵EF垂直平分BC,AC垂直平分BD,
∴BF=CF,
∴AE=EC,
∴AE=BE,
∴∠BAE=∠EBA,
∵∠C=110°,
∴∠ABC=70°,
∴∠EBA=∠EAB=35°,
∴∠EAD=110°﹣35°=75°,
故选:D.
7.【解答】解:A、AC=BD时, ABCD是矩形,故选项A符合题意;
B、AC⊥BD时, ABCD是菱形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵∠ACD=∠ACB,
∴∠DAC=∠ACD,
∴AD=CD,
∴ ABCD是菱形,故选项C不符合题意;
D、BC=CD时, ABCD是菱形,故选项D不符合题意;
故选:A.
8.【解答】解:∵四边形ABCD是菱形,
∴OA=OC,即点A与点C关于原点对称,
∵点A(﹣2,5),
∴点C的坐标是(2,﹣5).
故选:B.
9.【解答】解:如图:将菱形ABCD与△EAD构成的图形绕点O逆时针旋转,每次旋转45°,即点E绕点O逆时针旋转,每次旋转45°,过点E6作E6G⊥x轴,垂足为G,
∵360°÷45°=8,
∴点E每8次一循环,
∵2022÷8=252......6,
∴点E2022的坐标与点E6的坐标相同,
∵A(0,1),
∴OA=1,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ABO=∠CBO=∠ABC=30°,AB=AD,
∴∠ABD=∠ADB=30°,
在Rt△ADO中,AD=2OA=2,OD=OA=,
由题意得:
AD=DE=AE=2,
∴△ADE是等边三角形,
∴∠ADE=60°,
∴∠ODE=∠ADE+∠ADB=90°,
∴∠EOD+∠OED=90°,
由题意得:
OE=OE6,∠EOE6=2×45°=90°,
∴∠EOD+∠DOE6=90°,
∴∠OED=∠DOE6,
∵∠ODE=∠OGE6=90°,
∴△DOE≌△FE6O,
∴OD=FE6=,DE=FO=2,
∴E6(2,﹣),
∴E2022(2,﹣),
故选:D.
10.【解答】解:甲:∵四边形ABCD是菱形,
∴∠BAD=∠BCD,AB=BC=CD=AD,
∴∠BAC=∠DAC=∠BCA=∠DCA,
∴∠BAF=∠DAF=∠BCE=∠DCE,
在△BAF和△DAF中,
,
∴△BAF≌△DAF(SAS),
∴BF=DF,
同理:△DCE≌△BCE(SAS),△BAF≌△BCE(SAS),
∴BE=DE,BF=BE,
∴BF=DF=BE=DE,
∴四边形FBED是菱形;
乙:连接BD交AC于O,如图所示:
∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD,
∵AF=CE,
∴OA+AF=OC+CE,
即OF=OE,
∴四边形FBED是平行四边形,
又∵AC⊥BD,
∴平行四边形FBED是菱形;
综上所述,甲对、乙对,丙错,
故选:A.
二.填空题(共5小题)
11.【解答】解:∵四边形ABCD是菱形,
∴BO=DO,AC⊥DB,AO=CO,
∵BD=2cm,
∴BO=1cm,
∵AB=cm,
∴AO===2(cm),
∴AC=2AO=4cm.
∴S菱形ABCD=(cm2).
故答案为:4.
12.【解答】解:∵四边形ABCD为菱形,
∴OB=OD,
又∵点O为坐标原点,
∴点B和点D关于原点对称,
∵点B的坐标为(﹣1,﹣),
∴D点坐标为(1,),
故答案为:(1,).
13.【解答】解:∵ABCD是菱形,
∴BO=DO=6,AO=CO,S菱形ABCD=,
∴AC=8,
∵AH⊥BC,AO=CO=4,
∴OH=AC=4.
故答案为:4.
14.【解答】解:如图所示:连接BD交AC于点O,连接FO,取OB的中点H,连接HG和AH,
∵在菱形ABCD中,
∴O为AC中点,
∵F为CE中点,
∴OF=AE=1,
当C、F、E、A共线时,OF也为1,
∵G为BF中点、H为OB中点,
∴GH=OF=,
∵在菱形ABCD中且∠D=60°,
∴∠ABO=∠ABC=∠ADC=30°,∠BOA=90°,
∴OA=AB=2,
∴OB==,
∴OH=,
∴AH==,
∵AG≤AH+HG,
∴AG≤,
∴AG的最大值为.
故答案为:.
15.【解答】解:①过点A作AP⊥BC于点P,如图1:
∵△ABC是边长为1的等边三角形,AP⊥BC,
∴BP=BC=,
∴AP=,
∴.故①正确;
②当点D与点C重合时,H,D,C三点重合,如图2:
∵∠DBE=30°,∠ABC=60°,
∴BE是∠ABC的平分线,
∵AB=BC,
∴AE=EC=AC=,
∵CF∥AB,
∴∠FCA=∠A=60°,
∵GF∥BC,
∴∠FEC=∠ACB=60°,
∴∠FCE=∠FEC=60°,
∴∠FCE=∠FEC=∠F=60°,
∴△EFC为等边三角形,
∴FC=EC=,
即FH=.故②正确;
③如图3,将△CBD绕点B逆时针旋转60°,得到△ABN,连接NE,过点N作NP⊥AC,交CA的延长线于P,
∴BD=BN,CD=AN,∠BAN=∠C=60°,∠CBD=∠ABN,
∵∠DBE=30°,
∴∠CBD+∠ABE=30°=∠ABE+∠ABN=∠EBN,
∴∠EBN=∠DBE=30°,
又∵BD=BN,BE=BE,
∴△DBE≌△NBE(SAS),
∴DE=NE,
∵∠NAP=180°﹣∠BAC﹣∠NAB=60°,
∴AP=AN,NP=AP=AN=CD,
∵NP2+PE2=NE2,
∴CD2+(AE+CD)2=DE2,
∴AE2+CD2+AE CD=DE2,故③错误;
∵△ABC是等边三角形,
∴∠A=∠ABC=∠C=60°,
∵GF∥BH,BG∥HF,
∴四边形BHFG是平行四边形,
∵GF∥BH,BG∥HF,
∴∠AGE=∠ABC=60°,∠DHC=∠ABC=60°,
∴△AGE,△DCH都是等边三角形,
∴AG=AE,CH=CD,
∵AE=CD,
∴AG=CH,
∴BH=BG,
∴ BHFG是菱形,故④正确,
故答案为:①②④.
三.解答题(共5小题)
16.【解答】解:赞成小洁的说法,补充条件:OA=OC,证明如下:
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴平行四边形ABCD是菱形.
17.【解答】(1)证明:∵D、E分别是AC、AB的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∴EF∥BC,
∵BF∥CE,
∴四边形BCEF是平行四边形,
∵DE=CE,
∴BC=CE,
∴平行四边形BCEF是菱形;
(2)解:如图,过点E作EG⊥BC于点G,
由(1)知BC=CE,
∵∠BCE=60°,
∴△BCE是等边三角形,
∴BE=CE=BC=2,
∵EG⊥BC,
∴BG=BC=1,
在Rt△BGE中,由勾股定理得:EG===,
∴S菱形BCEF=BC EG=2×=2.
18.【解答】(1)证明:如图,连接BD,
∵四边形ABCD是菱形,
∴AC⊥DB,AD=AB,
∵EM⊥AC,
∴ME∥BD,
∵点E是AB的中点,
∴点M是AD的中点,AE=AB,
∴AM=AD,
∴AM=AE.
(2)解:①由(1)得,点M是AD的中点,
∴AM=MD,
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠F=∠AEM,∠EAM=∠FDM,
∴△MDF≌△MAE(AAS),
∴AE=DF,
∵AB=2AE,DF=2,
∴AB=4,
∴菱形ABCD的周长为4AB=4×4=16.
②如图,连接CM,记EF与AC交点为点G,
∵AM=AE,△MAE≌△MDF,
∴DF=DM,MF=ME,
∴∠DMF=∠DFM,
∴∠ADC=2∠DFM,
∵∠ADC=2∠MCD,
∴∠MCD=∠DFM,
∴MF=MC=ME,∠EMC=2∠F=∠MDC,
∵ME⊥AC,AM=AE,
∴∠MGC=90°,ME=2MG,
∴MC=2MG,
∴∠GMC=60°,
∴∠ADC=60°,
∴∠MCD=30°,
∴∠DMC=90°,
∴△DMC为直角三角形,
∵DF=2,
∴DM=2,CD=4,
∴CM==2,
∴ME=2.
19.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵BE⊥AD,BF⊥CD,
∴∠AEB=∠CFB=90°,
在△ABE和△CBF中,
,
∴△ABE≌△CBF(ASA),
∴AB=CB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴AD=AB=13,
设AE=x,则DE=13﹣x,
在Rt△ABE和Rt△BDE中,由勾股定理得:BE2=AB2﹣AE2=DB2﹣DE2,
即132﹣x2=102﹣(13﹣x)2,
解得:x=,
∴BE==,
∴平行四边形ABCD的面积=AD×BE=13×=120.
20.【解答】解:(1)如图,连接AC,
∵四边形ABCD为菱形,∠BAD=120°,
∴∠BAC=60°,
∵△AEF是等边三角形,
∴∠EAF=60°,
∴∠1+∠EAC=60°,∠3+∠EAC=60°,
∴∠1=∠3,
∵∠BAD=120°,
∴∠ABC=60°,
∴△ABC和△ACD为等边三角形,
∴∠4=60°,AC=AB,
∴在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA).
∴BE=CF;
(2)四边形AECF的面积不变,△CEF的周长发生变化.理由如下:
由(1)得△ABE≌△ACF,
则S△ABE=S△ACF,
故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值,
作AH⊥BC于H点,则BH=2,
S四边形AECF=S△ABC=.
△CEF的周长=CE+CF+EF=CE+BE+EF=BC+EF=BC+AE
由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短.
故△AEF的周长会随着AE的变化而变化,且当AE最短时,△CEF的周长会最小=4+
菱形的性质与判定 常考易错习题检测 (附带答案)
一.选择题(共10小题)
1.菱形具有而一般平行四边形不具有的性质是( )
A.对边平行 B.对边相等
C.对角线互相平分 D.对角线互相垂直
2.如图,菱形ABCD中,∠ABD=70°,则∠C的度数为( )
A.30° B.40° C.50° D.60°
3.菱形ABCD中,AC=10,BD=24,则该菱形的面积等于( )
A.13 B.52 C.120 D.240
4.如图,在菱形ABCD中,对角线AC,BD分别为16和12,DE⊥AB于点E,则DE=( )
A. B. C.10 D.8
5.如图, ABCD对角线AC,BD交于点O,请添加一个条件:____使得 ABCD是菱形( )
A.AB=AC B.AC⊥BD C.AB=CD D.AC=BD
6.如图,在菱形ABCD中,∠C=110°,BC的垂直平分线交BD于点E,F为垂足,连接AE,则∠EAD的度数是( )
A.60° B.65° C.70° D.75°
7. ABCD的对角线AC与BD相交于点O,添加以下条件,不能判定平行四边形ABCD为菱形的是( )
A.AC=BD B.AC⊥BD C.∠ACD=∠ACB D.BC=CD
8.如图,菱形ABCD对角线交点与坐标原点O重合,点A(﹣2,5),则点C的坐标是( )
A.(5,﹣2) B.(2,﹣5) C.(2,5) D.(﹣2,﹣5)
9.如图,在菱形ABCD中,顶点A,B,C,D在坐标轴上,且A(0,1),∠ABC=60°,分别以点A,D为圆心,以AD的长为半径作弧,两弧交于点E,连接EA,ED.将菱形ABCD与△EAD构成的图形绕点O逆时针旋转,每次旋转45°,则第2022次旋转结束时,点E2022的坐标为( )
A. B. C. D.
10.问题:已知:如图,四边形ABCD是菱形,E、F是直线AC上两点,AF=CE.求证:四边形FBED是菱形.
几名同学对这个问题,给出了如下几种解题思路,其中正确的是( )
甲:利用全等,证明四边形FBED四条边相等,进而说明该四边形是菱形;
乙:连接BD,利用对角线互相垂直的平行四边形是菱形,判定四边形FBED是菱形;
丙:该题目错误,根据已知条件不能够证明该四边形是菱形.
A.甲、乙对,丙错 B.乙、丙对,甲错
C.三个人都对 D.甲、丙对,乙错
二.填空题(共5小题)
11.如图,四边形ABCD是边长为cm的菱形,其中对角线BD的长为2cm,则菱形ABCD的面积为 cm2.
12.如图,已知点A的坐标是,2),点B的坐标是(﹣1,,菱形ABCD的对角线交于坐标原点O,则点D的坐标是 .
13.如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AH⊥BC于点H,连接OH,若OB=6,菱形ABCD的面积为48,则OH的长为 .
14.在菱形ABCD中,∠D=60°,CD=4,E为菱形内部一点,且AE=2,连接CE,点F为CE中点,连接BF,取BF中点G,连接AG,则AG的最大值为 .
15.如图,△ABC是边长为1的等边三角形,D,E为线段AC上两动点,且∠DBE=30°,过点D,E分别作AB,BC的平行线相交于点F,分别交BC,AB于点H,G.现有以下结论:①S△ABC=;②当点D与点C重合时,FH=;③AE+CD=DE;④当AE=CD时,四边形BHFG为菱形.则其中正确的结论的序号是 .
三.解答题(共5小题)
16.小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD交于点O,AC⊥BD,OB=OD.求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.
小惠: 证明:∵AC⊥BD,OB=OD, ∴AC垂直平分BD. ∴AB=AD,CB=CD, ∴四边形ABCD是菱形. 小洁: 这个题目还缺少条件,需要补充一个条件才能证明.
若赞同小惠的证法,请在第一个方框内打“√”;若赞成小洁的说法,请你补充一个条件,并证明.
17.如图,△ABC中,D,E分别是AC,AB的中点,DE=CE,过点B作BF∥CE,交DE的延长线于点F.
(1)求证:四边形BCEF是菱形.
(2)若BC=2,∠BCE=60°,求菱形BCEF的面积.
18.如图,四边形ABCD是菱形,E是AB的中点,AC的垂线EF交AD于点M,交CD的延长线于点F.
(1)求证:AM=AE;
(2)连接CM,DF=2.
①求菱形ABCD的周长;
②若∠ADC=2∠MCF,求ME的长.
19.如图,在平行四边形ABCD中,BE⊥AD,BF⊥CD,垂足分别为E,F,且AE=CF.
(1)求证:平行四边形ABCD是菱形;
(2)若DB=10,AB=13,求平行四边形ABCD的面积.
20.如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
(1)证明不论E、F在BC、CD上如何滑动,总有BE=CF;
(2)当点E、F在BC、CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:A.对边平行是菱形和一般平行四边形都具有的性质,故A不符合题意;
B.对边相等是菱形和一般平行四边形都具有的性质,故B不符合题意;
C.对角线互相平分是菱形和一般平行四边形都具有的性质,故C不符合题意;
D.对角线互相垂直是菱形具有而一般平行四边形不具有的性质,故D符合题意;
故选:D.
2.【解答】解:∵四边形ABCD是菱形,
∴∠ADC=∠ABC,DB平分∠ADC和∠ABC,
∴∠CDB=∠CBD=∠ADB=∠ABD=70°,
∴∠C=180°﹣2∠CDB=180°﹣2×70°=40°,
故选:B.
3.【解答】解:∵菱形对角线相互垂直,
∴AC⊥BD,
∴菱形面积是S=AC×BD==120.
故选:C.
4.【解答】解:如图,设AC与BD的交点为O,
∵四边形ABCD是菱形,
∴AO=CO=8,DO=BO=6,AC⊥BD,
∴AB===10,
∵S菱形ABCD=×AC×BD=AB×DE,
∴×16×12=10×DE,
∴DE=,
故选:A.
5.【解答】解:当AC⊥BD时, ABCD是菱形,
故选:B.
6.【解答】解:连接EC,AC,
∵EF垂直平分BC,AC垂直平分BD,
∴BF=CF,
∴AE=EC,
∴AE=BE,
∴∠BAE=∠EBA,
∵∠C=110°,
∴∠ABC=70°,
∴∠EBA=∠EAB=35°,
∴∠EAD=110°﹣35°=75°,
故选:D.
7.【解答】解:A、AC=BD时, ABCD是矩形,故选项A符合题意;
B、AC⊥BD时, ABCD是菱形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵∠ACD=∠ACB,
∴∠DAC=∠ACD,
∴AD=CD,
∴ ABCD是菱形,故选项C不符合题意;
D、BC=CD时, ABCD是菱形,故选项D不符合题意;
故选:A.
8.【解答】解:∵四边形ABCD是菱形,
∴OA=OC,即点A与点C关于原点对称,
∵点A(﹣2,5),
∴点C的坐标是(2,﹣5).
故选:B.
9.【解答】解:如图:将菱形ABCD与△EAD构成的图形绕点O逆时针旋转,每次旋转45°,即点E绕点O逆时针旋转,每次旋转45°,过点E6作E6G⊥x轴,垂足为G,
∵360°÷45°=8,
∴点E每8次一循环,
∵2022÷8=252......6,
∴点E2022的坐标与点E6的坐标相同,
∵A(0,1),
∴OA=1,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ABO=∠CBO=∠ABC=30°,AB=AD,
∴∠ABD=∠ADB=30°,
在Rt△ADO中,AD=2OA=2,OD=OA=,
由题意得:
AD=DE=AE=2,
∴△ADE是等边三角形,
∴∠ADE=60°,
∴∠ODE=∠ADE+∠ADB=90°,
∴∠EOD+∠OED=90°,
由题意得:
OE=OE6,∠EOE6=2×45°=90°,
∴∠EOD+∠DOE6=90°,
∴∠OED=∠DOE6,
∵∠ODE=∠OGE6=90°,
∴△DOE≌△FE6O,
∴OD=FE6=,DE=FO=2,
∴E6(2,﹣),
∴E2022(2,﹣),
故选:D.
10.【解答】解:甲:∵四边形ABCD是菱形,
∴∠BAD=∠BCD,AB=BC=CD=AD,
∴∠BAC=∠DAC=∠BCA=∠DCA,
∴∠BAF=∠DAF=∠BCE=∠DCE,
在△BAF和△DAF中,
,
∴△BAF≌△DAF(SAS),
∴BF=DF,
同理:△DCE≌△BCE(SAS),△BAF≌△BCE(SAS),
∴BE=DE,BF=BE,
∴BF=DF=BE=DE,
∴四边形FBED是菱形;
乙:连接BD交AC于O,如图所示:
∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD,
∵AF=CE,
∴OA+AF=OC+CE,
即OF=OE,
∴四边形FBED是平行四边形,
又∵AC⊥BD,
∴平行四边形FBED是菱形;
综上所述,甲对、乙对,丙错,
故选:A.
二.填空题(共5小题)
11.【解答】解:∵四边形ABCD是菱形,
∴BO=DO,AC⊥DB,AO=CO,
∵BD=2cm,
∴BO=1cm,
∵AB=cm,
∴AO===2(cm),
∴AC=2AO=4cm.
∴S菱形ABCD=(cm2).
故答案为:4.
12.【解答】解:∵四边形ABCD为菱形,
∴OB=OD,
又∵点O为坐标原点,
∴点B和点D关于原点对称,
∵点B的坐标为(﹣1,﹣),
∴D点坐标为(1,),
故答案为:(1,).
13.【解答】解:∵ABCD是菱形,
∴BO=DO=6,AO=CO,S菱形ABCD=,
∴AC=8,
∵AH⊥BC,AO=CO=4,
∴OH=AC=4.
故答案为:4.
14.【解答】解:如图所示:连接BD交AC于点O,连接FO,取OB的中点H,连接HG和AH,
∵在菱形ABCD中,
∴O为AC中点,
∵F为CE中点,
∴OF=AE=1,
当C、F、E、A共线时,OF也为1,
∵G为BF中点、H为OB中点,
∴GH=OF=,
∵在菱形ABCD中且∠D=60°,
∴∠ABO=∠ABC=∠ADC=30°,∠BOA=90°,
∴OA=AB=2,
∴OB==,
∴OH=,
∴AH==,
∵AG≤AH+HG,
∴AG≤,
∴AG的最大值为.
故答案为:.
15.【解答】解:①过点A作AP⊥BC于点P,如图1:
∵△ABC是边长为1的等边三角形,AP⊥BC,
∴BP=BC=,
∴AP=,
∴.故①正确;
②当点D与点C重合时,H,D,C三点重合,如图2:
∵∠DBE=30°,∠ABC=60°,
∴BE是∠ABC的平分线,
∵AB=BC,
∴AE=EC=AC=,
∵CF∥AB,
∴∠FCA=∠A=60°,
∵GF∥BC,
∴∠FEC=∠ACB=60°,
∴∠FCE=∠FEC=60°,
∴∠FCE=∠FEC=∠F=60°,
∴△EFC为等边三角形,
∴FC=EC=,
即FH=.故②正确;
③如图3,将△CBD绕点B逆时针旋转60°,得到△ABN,连接NE,过点N作NP⊥AC,交CA的延长线于P,
∴BD=BN,CD=AN,∠BAN=∠C=60°,∠CBD=∠ABN,
∵∠DBE=30°,
∴∠CBD+∠ABE=30°=∠ABE+∠ABN=∠EBN,
∴∠EBN=∠DBE=30°,
又∵BD=BN,BE=BE,
∴△DBE≌△NBE(SAS),
∴DE=NE,
∵∠NAP=180°﹣∠BAC﹣∠NAB=60°,
∴AP=AN,NP=AP=AN=CD,
∵NP2+PE2=NE2,
∴CD2+(AE+CD)2=DE2,
∴AE2+CD2+AE CD=DE2,故③错误;
∵△ABC是等边三角形,
∴∠A=∠ABC=∠C=60°,
∵GF∥BH,BG∥HF,
∴四边形BHFG是平行四边形,
∵GF∥BH,BG∥HF,
∴∠AGE=∠ABC=60°,∠DHC=∠ABC=60°,
∴△AGE,△DCH都是等边三角形,
∴AG=AE,CH=CD,
∵AE=CD,
∴AG=CH,
∴BH=BG,
∴ BHFG是菱形,故④正确,
故答案为:①②④.
三.解答题(共5小题)
16.【解答】解:赞成小洁的说法,补充条件:OA=OC,证明如下:
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴平行四边形ABCD是菱形.
17.【解答】(1)证明:∵D、E分别是AC、AB的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∴EF∥BC,
∵BF∥CE,
∴四边形BCEF是平行四边形,
∵DE=CE,
∴BC=CE,
∴平行四边形BCEF是菱形;
(2)解:如图,过点E作EG⊥BC于点G,
由(1)知BC=CE,
∵∠BCE=60°,
∴△BCE是等边三角形,
∴BE=CE=BC=2,
∵EG⊥BC,
∴BG=BC=1,
在Rt△BGE中,由勾股定理得:EG===,
∴S菱形BCEF=BC EG=2×=2.
18.【解答】(1)证明:如图,连接BD,
∵四边形ABCD是菱形,
∴AC⊥DB,AD=AB,
∵EM⊥AC,
∴ME∥BD,
∵点E是AB的中点,
∴点M是AD的中点,AE=AB,
∴AM=AD,
∴AM=AE.
(2)解:①由(1)得,点M是AD的中点,
∴AM=MD,
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠F=∠AEM,∠EAM=∠FDM,
∴△MDF≌△MAE(AAS),
∴AE=DF,
∵AB=2AE,DF=2,
∴AB=4,
∴菱形ABCD的周长为4AB=4×4=16.
②如图,连接CM,记EF与AC交点为点G,
∵AM=AE,△MAE≌△MDF,
∴DF=DM,MF=ME,
∴∠DMF=∠DFM,
∴∠ADC=2∠DFM,
∵∠ADC=2∠MCD,
∴∠MCD=∠DFM,
∴MF=MC=ME,∠EMC=2∠F=∠MDC,
∵ME⊥AC,AM=AE,
∴∠MGC=90°,ME=2MG,
∴MC=2MG,
∴∠GMC=60°,
∴∠ADC=60°,
∴∠MCD=30°,
∴∠DMC=90°,
∴△DMC为直角三角形,
∵DF=2,
∴DM=2,CD=4,
∴CM==2,
∴ME=2.
19.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵BE⊥AD,BF⊥CD,
∴∠AEB=∠CFB=90°,
在△ABE和△CBF中,
,
∴△ABE≌△CBF(ASA),
∴AB=CB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴AD=AB=13,
设AE=x,则DE=13﹣x,
在Rt△ABE和Rt△BDE中,由勾股定理得:BE2=AB2﹣AE2=DB2﹣DE2,
即132﹣x2=102﹣(13﹣x)2,
解得:x=,
∴BE==,
∴平行四边形ABCD的面积=AD×BE=13×=120.
20.【解答】解:(1)如图,连接AC,
∵四边形ABCD为菱形,∠BAD=120°,
∴∠BAC=60°,
∵△AEF是等边三角形,
∴∠EAF=60°,
∴∠1+∠EAC=60°,∠3+∠EAC=60°,
∴∠1=∠3,
∵∠BAD=120°,
∴∠ABC=60°,
∴△ABC和△ACD为等边三角形,
∴∠4=60°,AC=AB,
∴在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA).
∴BE=CF;
(2)四边形AECF的面积不变,△CEF的周长发生变化.理由如下:
由(1)得△ABE≌△ACF,
则S△ABE=S△ACF,
故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值,
作AH⊥BC于H点,则BH=2,
S四边形AECF=S△ABC=.
△CEF的周长=CE+CF+EF=CE+BE+EF=BC+EF=BC+AE
由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短.
故△AEF的周长会随着AE的变化而变化,且当AE最短时,△CEF的周长会最小=4+
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
