北师大版九年级数学上册 1.2矩形的性质与判定 同步达标测试题(含解析)
文档属性
| 名称 | 北师大版九年级数学上册 1.2矩形的性质与判定 同步达标测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 218.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 18:32:45 | ||
图片预览



文档简介
2022-2023学年北师大版九年级数学上册《1.2矩形的性质与判定》
同步达标测试题(附答案)
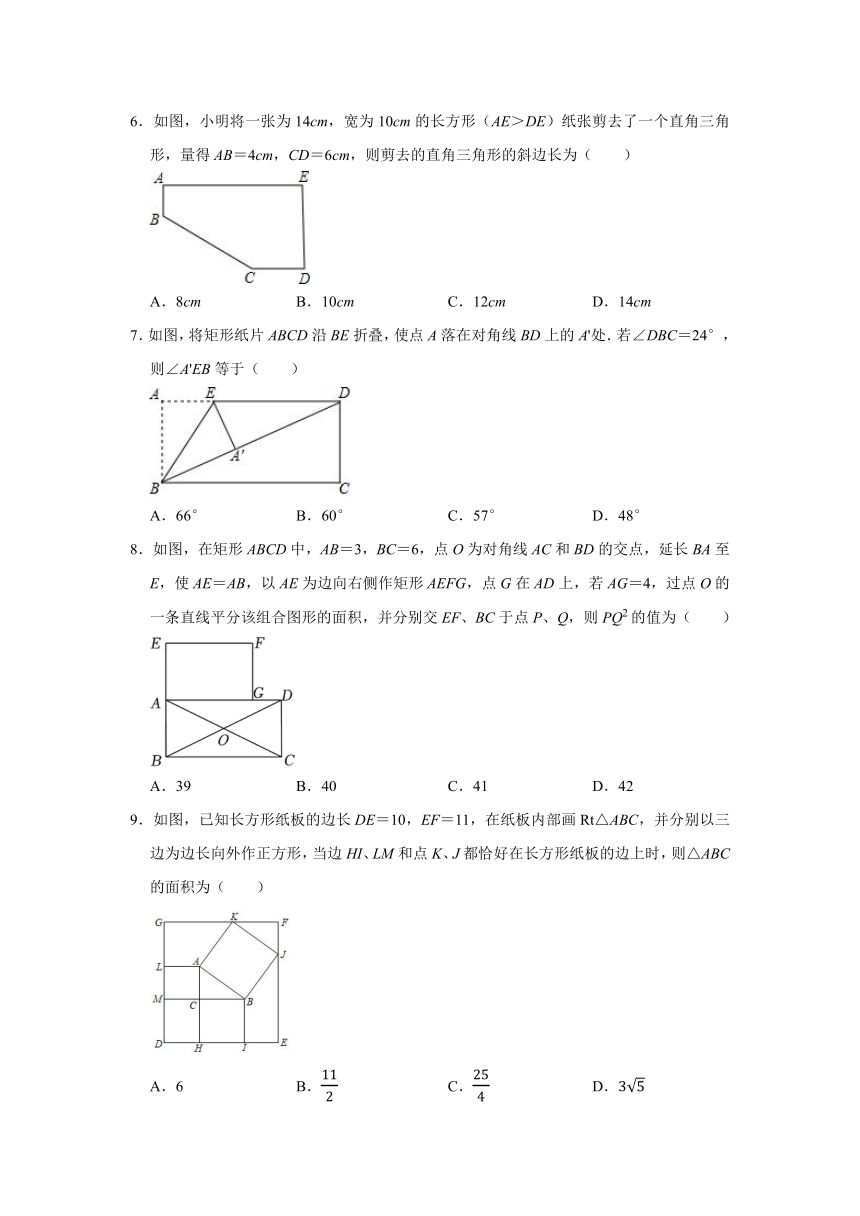
一.选择题(共9小题,满分27分)
1.矩形具有而一般平行四边形不具有的性质是( )
A.两组对边分别相等 B.两组对角分别相等
C.两条对角线互相平分 D.两条对角线相等
2.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AC⊥BD C.∠ABC=90° D.∠1=∠2
3.如图,矩形ABCD中,对角线AC,BD交于O点.若∠BOC=120°,AC=8,则AB的长为( )
A.6 B.4 C. D.
4.如图,在矩形ABCD中,AB=3,AD=4,点E在边BC上,连接DE,若AE平分∠BED,则EC的长为( )
A. B. C. D.
5.如图,在矩形ABCD中,∠BDC的平分线交AB的延长线于点E,若AD=3,AE=9,则AB的长为( )
A.3.5 B.4 C.4.5 D.5
6.如图,小明将一张为14cm,宽为10cm的长方形(AE>DE)纸张剪去了一个直角三角形,量得AB=4cm,CD=6cm,则剪去的直角三角形的斜边长为( )
A.8cm B.10cm C.12cm D.14cm
7.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66° B.60° C.57° D.48°
8.如图,在矩形ABCD中,AB=3,BC=6,点O为对角线AC和BD的交点,延长BA至E,使AE=AB,以AE为边向右侧作矩形AEFG,点G在AD上,若AG=4,过点O的一条直线平分该组合图形的面积,并分别交EF、BC于点P、Q,则PQ2的值为( )
A.39 B.40 C.41 D.42
9.如图,已知长方形纸板的边长DE=10,EF=11,在纸板内部画Rt△ABC,并分别以三边为边长向外作正方形,当边HI、LM和点K、J都恰好在长方形纸板的边上时,则△ABC的面积为( )
A.6 B. C. D.
二.填空题(共10小题,满分40分)
10.如图,四边形ABDE是长方形,AC⊥DC于点C,交BD于点F,AE=AC,∠ADE=62°,则∠BAF的度数为 .
11.如图,若将四根木条钉成的矩形木框ABCD变形为平行四边形A′BCD′,并使其面积为矩形ABCD面积的一半,若A′D′与CD交于点E,且AB=2,则△ECD′的面积是 .
12.如图,矩形ABCD中,AC的垂直平分线MN与AB交于点E,连接CE.若∠CAD=70°,则∠DCE= °.
13.如图,矩形ABCD中,AC,BD交于点O,M,N分别为BC,OC的中点,若MN=3,则BD= .
14.如图, ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点N,连接EM.若 ABCD的周长为42cm,FM=6cm,EF=8cm,则EM= cm,AB= cm.
15.如图所示,线段BC为等腰△ABC的底边,矩形ADBE的对角线AB与DE交于点O,若OD=2,则AC= .
16.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为 .
17.已知平面上四点A(0,0),B(10,0),C(10,6),D(0,6),直线y=mx﹣3m+2将四边形ABCD分成面积相等的两部分,则m的值为 .
18.如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为 .
19.如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快 s后,四边形ABPQ成为矩形.
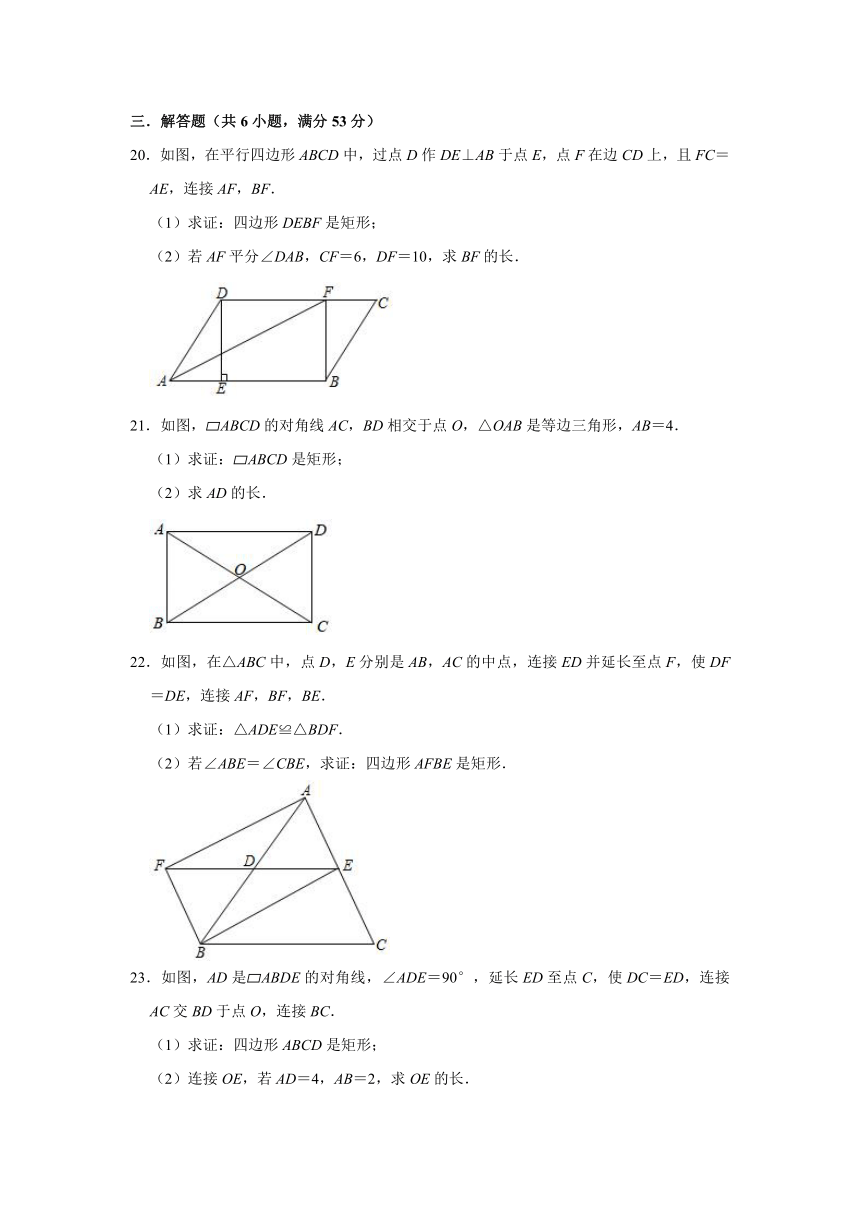
三.解答题(共6小题,满分53分)
20.如图,在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,且FC=AE,连接AF,BF.
(1)求证:四边形DEBF是矩形;
(2)若AF平分∠DAB,CF=6,DF=10,求BF的长.
21.如图, ABCD的对角线AC,BD相交于点O,△OAB是等边三角形,AB=4.
(1)求证: ABCD是矩形;
(2)求AD的长.
22.如图,在△ABC中,点D,E分别是AB,AC的中点,连接ED并延长至点F,使DF=DE,连接AF,BF,BE.
(1)求证:△ADE≌△BDF.
(2)若∠ABE=∠CBE,求证:四边形AFBE是矩形.
23.如图,AD是 ABDE的对角线,∠ADE=90°,延长ED至点C,使DC=ED,连接AC交BD于点O,连接BC.
(1)求证:四边形ABCD是矩形;
(2)连接OE,若AD=4,AB=2,求OE的长.
24.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)DF⊥AC,若∠ADF:∠FDC=2:1,则∠BDF的度数是多少?
25.如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若∠BDE=15°,求∠DOE;
(3)在(2)的条件下,若AB=2,求△BOE的面积.
参考答案
一.选择题(共9小题,满分27分)
1.解:A、矩形、平行四边形的对边都是相等的,故本选项不符合;
B、矩形、平行四边形的对角都是相等的,故本选项不符合;
C、矩形、平行四边形的对角线都是互相平分的,故本选项不符合;
D、矩形的对角线相等,平行四边形的对角线不一定相等,故本选项符合;
故选:D.
2.解:A、是邻边相等,可判定平行四边形ABCD是菱形;
B、是对角线互相垂直,可判定平行四边形ABCD是菱形;
C、是一内角等于90°,可判断平行四边形ABCD成为矩形;
D、是对角线平分对角,可判定平行四边形ABCD是菱形.
故选:C.
3.解:∵四边形ABCD是矩形,
∴OAAC=4,OBBD,AC=BD,
∴OA=OB=4,
∵∠BOC=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=4;
故选:B.
4.解:∵四边形ABCD是矩形,
∴AD∥BC,AB=CD=3,
∴∠DAE=∠AEB,
∵AE平分∠BED,
∴∠AED=∠AEB,
∴∠AED=∠DAE,
∴AD=DE=4,
∴EC,
故选:C.
5.解:∵四边形ABCD是矩形,
∴CD∥AB,
∴∠CDE=∠E.
又∵∠BDC的平分线交AB的延长线于点E,
∴∠CDE=∠BDE,
∴∠BDE=∠E.
∴BE=BD.
∵AE=9,
∴BD=BE=9﹣AB.
∵DB2=AD2+AB2,
∴(9﹣AB)2=9+AB2,
∴AB=4,
故选:B.
6.解:延长AB、DC相交于F,则△BFC是直角三角形,
在Rt△BFC中,BC2=(14﹣6)2+(10﹣4)2=82+62=100,
所以BC=10.
则剪去的直角三角形的斜边长为10cm,
故选:B.
7.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,
由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,
∴∠A'BE=∠ABE(90°﹣∠DBC)(90°﹣24°)=33°,
∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°.
故选:C.
8.解:∵过点O的一条直线平分该组合图形的面积,
∴PQ必过矩形EFGA的对角线交点,
连接AF,EG交于点H,取AE的中点M,AB的中点N,连接HM,ON,过点H作HT⊥ON于T,设PQ与AD的交点为S,
∵四边形ABCD是矩形,
∴AO=CO,
又∵点N是AB的中点,
∴ONBC=3,AN,ON∥BC,
∴∠ANO=∠ABC=90°,
同理可求:NH=2,AM,∠AMH=90°,
∵HT⊥NO,
∴四边形MHTN是矩形,
∴MH=NT=2,MT=MN=3,
∴TO=1,
∴HO,
∵AD∥BC,
∴∠DAC=∠BCA,∠ASO=∠CQO,
在△ASO和△CQO中,
,
∴△ASO≌△CQO(AAS),
∴SO=OQ,
同理可得PH=SH,
∴PQ=2HO=2,
∴PQ2=40,
故选:B.
9.解:如图,延长CA交GF于R,延长CB交EF于Q,
∵四边形ACML,ABJK是正方形,
∴AC=CM,CM⊥GD,AB=BJ,∠ABJ=90°,
∵四边形GFED是矩形,
∴GD∥EF,
∴MC⊥EF,
∴∠BQJ=∠ACB=90°=∠ABJ,
∴∠ABC+∠BAC=90°=∠ABC+∠QBJ,
∴∠BAC=∠QBJ,
在△ABC和△BJQ中,
,
∴△ABC≌△BJQ(AAS),
∴AC=BQ,
同理可证:AR=BC,
∵AC+CH+AR=11,MC+BC+BQ=10,
∴AC+2BC=11,2AC+BC=10,
∴AC=3,BC=4,
∴S△ABCAC×BC3×4=6,
故选:A.
二.填空题(共10小题,满分40分)
10.解:∵四边形ABDE是矩形,
∴∠BAE=∠E=90°,
∵∠ADE=62°,
∴∠EAD=28°,
∵AC⊥CD,
∴∠C=∠E=90°
∵AE=AC,AD=AD,
∴Rt△ACD≌Rt△AED(HL)
∴∠EAD=∠CAD=28°,
∴∠BAF=90°﹣28°﹣28°=34°,
故答案为:34°.
11.解:作A'F⊥BC于F,如图所示:
则∠A'FB=90°,
根据题意得:平行四边形A′BCD′的面积=BC A'FBC AB,
∴A'FAB=1,
∴∠D'=∠A'BF=30°,
∴BFA'F,
∵四边形ABCD是矩形,四边形A′BCD′是平行四边形,
∴BC=AD=A'D',A'D'∥AD∥BC,CD⊥BC,
∴CD⊥A'D',
∴A'F∥CD,
∴四边形A'ECF是矩形,
∴CE=A'F=1,A'E=CF,
∴D'E=BF,
∴△ECD'的面积D'E×CE1;
故答案为:.
12.解:∵MN是AC的垂直平分线,
∴EC=EA,
∴∠ECA=∠EAC,
∵四边形ABCD是矩形,
∴AB∥CD,∠D=90°,
∴∠DCA=∠EAC=90°﹣70°=20°,
∴∠DCE=∠DCA+∠ECA=20°+20°=40°,
故答案为:40.
13.解:∵M、N分别为BC、OC的中点,
∴BO=2MN=6.
∵四边形ABCD是矩形,
∴BD=2BO=12.
故答案为12.
14.解:∵AE为∠DAB的平分线,
∴∠DAE=∠EAB∠DAB,
同理:∠ABE=∠CBE∠ABC,
∠BCM=∠DCM∠BCD,
∠CDM=∠ADM∠ADC.
∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,∠ABC=∠ADC,AD=BC.
∴∠DAF=∠BCN,∠ADF=∠CBN.
在△ADF和△CBN中,
∴△ADF≌△CBN(ASA).
∴DF=BN.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB+∠ABC=180°.
∴∠EAB+∠EBA=90°.
∴∠AEB=90°.
同理可得:∠AFD=∠DMC=90°.
∴∠EFM=90°.
∵FM=6,EF=8,
∴ME10(cm).
∵∠EFM=∠FMN=∠FEN=90°.
∴四边形EFMN是矩形.
∴EN=FM=6.
∵∠DAF=∠EAB,∠AFD=∠AEB,
∴8DF=6AF.
设DF=6k,则AF=8k.
∵∠AFD=90°,
∴AD=10k.
∵∠AEB=90°,AE=8(k+1),BE=6(k+1),
∴AB=10(k+1).
∵2(AB+AD)=42,
∴AB+AD=21.
∴10(k+1)+10k=21.
∴k=0.55.
∴AB=15.5(cm).
故答案为:10;15.5.
15.解:∵四边形ADBE是矩形,
∴AB=DE,AO=BO,DO=OE,
∴AB=DE=2OD=4,
∵AB=AC,
∴AC=4,
故答案为4.
16.解:∵四边形ABCD是矩形,
∴OA=OC,∠AEO=∠CFO;
又∵∠AOE=∠COF,
在△AOE和△COF中,
,
∴△AOE≌△COF,
∴S△AOE=S△COF,
∴图中阴影部分的面积就是△BCD的面积.
S△BCDBC×CD2×3=3.
故答案为:3.
17.解:∵直线y=mx﹣3m+2将四边形ABCD分成面积相等的两部分
∴直线必经过矩形的中心对称点O
∵根据矩形中心对称,可知O(5,3),将它代入y=mx﹣3m+2中得:
3=5m﹣3m+2,即m.
18.解:连接AD,
∵∠BAC=90°,且BA=3,AC=4,
∴BC5,
∵DM⊥AB,DN⊥AC,
∴∠DMA=∠DNA=∠BAC=90°,
∴四边形DMAN是矩形,
∴MN=AD,
∴当AD⊥BC时,AD的值最小,
此时,△ABC的面积AB×ACBC×AD,
∴AD,
∴MN的最小值为;
故答案为:.
19.解;设最快x秒,四边形ABPQ成为矩形,由BP=AQ得
3x=20﹣2x.
解得x=4,
故答案为:4.
三.解答题(共6小题,满分53分)
20.(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB,
∵FC=AE,
∴CD﹣FC=AB﹣AE,
即DF=BE,
∴四边形DEBF是平行四边形,
又∵DE⊥AB,
∴∠DEB=90°,
∴平行四边形DEBF是矩形;
(2)解:∵AF平分∠DAB,
∴∠DAF=∠BAF,
∵DC∥AB,
∴∠DFA=∠BAF,
∴∠DFA=∠DAF,
∴AD=DF=10,
在Rt△AED中,由勾股定理得:DE8,
由(1)得:四边形DEBF是矩形,
∴BF=DE=8.
21.(1)证明:∵△AOB为等边三角形,
∴∠BAO=∠AOB=60°,OA=OB,
∵四边形ABCD是平行四边形
∴OB=ODBD,OA=OCAC,
∴BD=AC,
∴ ABCD是矩形;
(2)解:∵ ABCD是矩形,
∴∠BAD=90°,
∵∠ABO=60°,
∴∠ADB=90°﹣60°=30°,
∴ADAB=4.
22.证明:(1)∵点D是AB的中点,
∴AD=BD,
在△ADE和△BDF中,
,
∴△ADE≌△BDF(SAS);
(2)∵AD=BD,DF=DE,
∴四边形AFBE是平行四边形,
∵点D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,
∴∠DEB=∠CBE,
∵∠ABE=∠CBE,
∴∠DEB=∠ABE,
∴DB=DE,
∴AB=EF,
∴平行四边形AFBE是矩形.
23.(1)证明:∵四边形ABDE是平行四边形,
∴AB∥DE,AB=ED,
∵DC=ED,
∴DC=AB,DC∥AB,
∴四边形ABCD是平行四边形,
∵DE⊥AD,
∴∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:过O作OF⊥CD于F,
∵四边形ABCD是矩形,AD=4,AB=2
∴DE=CD=AB=2,AD=BC=4,AC=BD,AO=OC,BO=DO,
∴OD=OC,
∵OF⊥CD,
∴DF=CFCD1,
∴OFBC2,EF=DE+DF=2+1=3,
∴OE.
24.(1)证明:∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠ADC=90°,
∴平行四边形ABCD是矩形;
(2)解:由(1)得:∠ADC=90°,四边形ABCD是矩形,
∵∠ADF:∠FDC=2:1,AC=BD,
∴∠FDC=30°,
∵DF⊥AC,
∴∠DCO=90°﹣30°=60°,
∵AO=CO,BO=DO,
∴OC=OD,
∴∠ODC=∠DCO=60°,
∴∠BDF=∠ODC﹣∠FDC=30°.
25.(1)证明:∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC=90°,
∴∠BAD=90°,
∴∠BAD=∠ABC=∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,DE平分∠ADC,
∴∠CDE=∠CED=45°,
∴EC=DC,
又∵∠BDE=15°,
∴∠CDO=60°,
又∵矩形的对角线互相平分且相等,
∴OD=OC,
∴△OCD是等边三角形,
∴∠DOC=∠OCD=60°,
∴∠OCB=90°﹣∠DCO=30°,
∵CO=CE,
∴∠COE=(180°﹣30°)÷2=75°,
∴∠DOE=∠DOC+∠COE=60°+75°=135°;
(3)解:作OF⊥BC于F.
∵四边形ABCD是矩形,
∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD,
∴AO=BO=CO=DO,
∴BF=FC,
∴OFCD=1,
∵∠OCB=30°,AB=2,
∴BC=2,
∵DE平分∠ADC,∠ADC=90°,
∴∠EDC=45°,
在Rt△EDC中,EC=CD=2,
∴△BOE的面积 EB OF(22)×11.
同步达标测试题(附答案)
一.选择题(共9小题,满分27分)
1.矩形具有而一般平行四边形不具有的性质是( )
A.两组对边分别相等 B.两组对角分别相等
C.两条对角线互相平分 D.两条对角线相等
2.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AC⊥BD C.∠ABC=90° D.∠1=∠2
3.如图,矩形ABCD中,对角线AC,BD交于O点.若∠BOC=120°,AC=8,则AB的长为( )
A.6 B.4 C. D.
4.如图,在矩形ABCD中,AB=3,AD=4,点E在边BC上,连接DE,若AE平分∠BED,则EC的长为( )
A. B. C. D.
5.如图,在矩形ABCD中,∠BDC的平分线交AB的延长线于点E,若AD=3,AE=9,则AB的长为( )
A.3.5 B.4 C.4.5 D.5
6.如图,小明将一张为14cm,宽为10cm的长方形(AE>DE)纸张剪去了一个直角三角形,量得AB=4cm,CD=6cm,则剪去的直角三角形的斜边长为( )
A.8cm B.10cm C.12cm D.14cm
7.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66° B.60° C.57° D.48°
8.如图,在矩形ABCD中,AB=3,BC=6,点O为对角线AC和BD的交点,延长BA至E,使AE=AB,以AE为边向右侧作矩形AEFG,点G在AD上,若AG=4,过点O的一条直线平分该组合图形的面积,并分别交EF、BC于点P、Q,则PQ2的值为( )
A.39 B.40 C.41 D.42
9.如图,已知长方形纸板的边长DE=10,EF=11,在纸板内部画Rt△ABC,并分别以三边为边长向外作正方形,当边HI、LM和点K、J都恰好在长方形纸板的边上时,则△ABC的面积为( )
A.6 B. C. D.
二.填空题(共10小题,满分40分)
10.如图,四边形ABDE是长方形,AC⊥DC于点C,交BD于点F,AE=AC,∠ADE=62°,则∠BAF的度数为 .
11.如图,若将四根木条钉成的矩形木框ABCD变形为平行四边形A′BCD′,并使其面积为矩形ABCD面积的一半,若A′D′与CD交于点E,且AB=2,则△ECD′的面积是 .
12.如图,矩形ABCD中,AC的垂直平分线MN与AB交于点E,连接CE.若∠CAD=70°,则∠DCE= °.
13.如图,矩形ABCD中,AC,BD交于点O,M,N分别为BC,OC的中点,若MN=3,则BD= .
14.如图, ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点N,连接EM.若 ABCD的周长为42cm,FM=6cm,EF=8cm,则EM= cm,AB= cm.
15.如图所示,线段BC为等腰△ABC的底边,矩形ADBE的对角线AB与DE交于点O,若OD=2,则AC= .
16.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为 .
17.已知平面上四点A(0,0),B(10,0),C(10,6),D(0,6),直线y=mx﹣3m+2将四边形ABCD分成面积相等的两部分,则m的值为 .
18.如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为 .
19.如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快 s后,四边形ABPQ成为矩形.
三.解答题(共6小题,满分53分)
20.如图,在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,且FC=AE,连接AF,BF.
(1)求证:四边形DEBF是矩形;
(2)若AF平分∠DAB,CF=6,DF=10,求BF的长.
21.如图, ABCD的对角线AC,BD相交于点O,△OAB是等边三角形,AB=4.
(1)求证: ABCD是矩形;
(2)求AD的长.
22.如图,在△ABC中,点D,E分别是AB,AC的中点,连接ED并延长至点F,使DF=DE,连接AF,BF,BE.
(1)求证:△ADE≌△BDF.
(2)若∠ABE=∠CBE,求证:四边形AFBE是矩形.
23.如图,AD是 ABDE的对角线,∠ADE=90°,延长ED至点C,使DC=ED,连接AC交BD于点O,连接BC.
(1)求证:四边形ABCD是矩形;
(2)连接OE,若AD=4,AB=2,求OE的长.
24.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)DF⊥AC,若∠ADF:∠FDC=2:1,则∠BDF的度数是多少?
25.如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若∠BDE=15°,求∠DOE;
(3)在(2)的条件下,若AB=2,求△BOE的面积.
参考答案
一.选择题(共9小题,满分27分)
1.解:A、矩形、平行四边形的对边都是相等的,故本选项不符合;
B、矩形、平行四边形的对角都是相等的,故本选项不符合;
C、矩形、平行四边形的对角线都是互相平分的,故本选项不符合;
D、矩形的对角线相等,平行四边形的对角线不一定相等,故本选项符合;
故选:D.
2.解:A、是邻边相等,可判定平行四边形ABCD是菱形;
B、是对角线互相垂直,可判定平行四边形ABCD是菱形;
C、是一内角等于90°,可判断平行四边形ABCD成为矩形;
D、是对角线平分对角,可判定平行四边形ABCD是菱形.
故选:C.
3.解:∵四边形ABCD是矩形,
∴OAAC=4,OBBD,AC=BD,
∴OA=OB=4,
∵∠BOC=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=4;
故选:B.
4.解:∵四边形ABCD是矩形,
∴AD∥BC,AB=CD=3,
∴∠DAE=∠AEB,
∵AE平分∠BED,
∴∠AED=∠AEB,
∴∠AED=∠DAE,
∴AD=DE=4,
∴EC,
故选:C.
5.解:∵四边形ABCD是矩形,
∴CD∥AB,
∴∠CDE=∠E.
又∵∠BDC的平分线交AB的延长线于点E,
∴∠CDE=∠BDE,
∴∠BDE=∠E.
∴BE=BD.
∵AE=9,
∴BD=BE=9﹣AB.
∵DB2=AD2+AB2,
∴(9﹣AB)2=9+AB2,
∴AB=4,
故选:B.
6.解:延长AB、DC相交于F,则△BFC是直角三角形,
在Rt△BFC中,BC2=(14﹣6)2+(10﹣4)2=82+62=100,
所以BC=10.
则剪去的直角三角形的斜边长为10cm,
故选:B.
7.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,
由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,
∴∠A'BE=∠ABE(90°﹣∠DBC)(90°﹣24°)=33°,
∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°.
故选:C.
8.解:∵过点O的一条直线平分该组合图形的面积,
∴PQ必过矩形EFGA的对角线交点,
连接AF,EG交于点H,取AE的中点M,AB的中点N,连接HM,ON,过点H作HT⊥ON于T,设PQ与AD的交点为S,
∵四边形ABCD是矩形,
∴AO=CO,
又∵点N是AB的中点,
∴ONBC=3,AN,ON∥BC,
∴∠ANO=∠ABC=90°,
同理可求:NH=2,AM,∠AMH=90°,
∵HT⊥NO,
∴四边形MHTN是矩形,
∴MH=NT=2,MT=MN=3,
∴TO=1,
∴HO,
∵AD∥BC,
∴∠DAC=∠BCA,∠ASO=∠CQO,
在△ASO和△CQO中,
,
∴△ASO≌△CQO(AAS),
∴SO=OQ,
同理可得PH=SH,
∴PQ=2HO=2,
∴PQ2=40,
故选:B.
9.解:如图,延长CA交GF于R,延长CB交EF于Q,
∵四边形ACML,ABJK是正方形,
∴AC=CM,CM⊥GD,AB=BJ,∠ABJ=90°,
∵四边形GFED是矩形,
∴GD∥EF,
∴MC⊥EF,
∴∠BQJ=∠ACB=90°=∠ABJ,
∴∠ABC+∠BAC=90°=∠ABC+∠QBJ,
∴∠BAC=∠QBJ,
在△ABC和△BJQ中,
,
∴△ABC≌△BJQ(AAS),
∴AC=BQ,
同理可证:AR=BC,
∵AC+CH+AR=11,MC+BC+BQ=10,
∴AC+2BC=11,2AC+BC=10,
∴AC=3,BC=4,
∴S△ABCAC×BC3×4=6,
故选:A.
二.填空题(共10小题,满分40分)
10.解:∵四边形ABDE是矩形,
∴∠BAE=∠E=90°,
∵∠ADE=62°,
∴∠EAD=28°,
∵AC⊥CD,
∴∠C=∠E=90°
∵AE=AC,AD=AD,
∴Rt△ACD≌Rt△AED(HL)
∴∠EAD=∠CAD=28°,
∴∠BAF=90°﹣28°﹣28°=34°,
故答案为:34°.
11.解:作A'F⊥BC于F,如图所示:
则∠A'FB=90°,
根据题意得:平行四边形A′BCD′的面积=BC A'FBC AB,
∴A'FAB=1,
∴∠D'=∠A'BF=30°,
∴BFA'F,
∵四边形ABCD是矩形,四边形A′BCD′是平行四边形,
∴BC=AD=A'D',A'D'∥AD∥BC,CD⊥BC,
∴CD⊥A'D',
∴A'F∥CD,
∴四边形A'ECF是矩形,
∴CE=A'F=1,A'E=CF,
∴D'E=BF,
∴△ECD'的面积D'E×CE1;
故答案为:.
12.解:∵MN是AC的垂直平分线,
∴EC=EA,
∴∠ECA=∠EAC,
∵四边形ABCD是矩形,
∴AB∥CD,∠D=90°,
∴∠DCA=∠EAC=90°﹣70°=20°,
∴∠DCE=∠DCA+∠ECA=20°+20°=40°,
故答案为:40.
13.解:∵M、N分别为BC、OC的中点,
∴BO=2MN=6.
∵四边形ABCD是矩形,
∴BD=2BO=12.
故答案为12.
14.解:∵AE为∠DAB的平分线,
∴∠DAE=∠EAB∠DAB,
同理:∠ABE=∠CBE∠ABC,
∠BCM=∠DCM∠BCD,
∠CDM=∠ADM∠ADC.
∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,∠ABC=∠ADC,AD=BC.
∴∠DAF=∠BCN,∠ADF=∠CBN.
在△ADF和△CBN中,
∴△ADF≌△CBN(ASA).
∴DF=BN.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB+∠ABC=180°.
∴∠EAB+∠EBA=90°.
∴∠AEB=90°.
同理可得:∠AFD=∠DMC=90°.
∴∠EFM=90°.
∵FM=6,EF=8,
∴ME10(cm).
∵∠EFM=∠FMN=∠FEN=90°.
∴四边形EFMN是矩形.
∴EN=FM=6.
∵∠DAF=∠EAB,∠AFD=∠AEB,
∴8DF=6AF.
设DF=6k,则AF=8k.
∵∠AFD=90°,
∴AD=10k.
∵∠AEB=90°,AE=8(k+1),BE=6(k+1),
∴AB=10(k+1).
∵2(AB+AD)=42,
∴AB+AD=21.
∴10(k+1)+10k=21.
∴k=0.55.
∴AB=15.5(cm).
故答案为:10;15.5.
15.解:∵四边形ADBE是矩形,
∴AB=DE,AO=BO,DO=OE,
∴AB=DE=2OD=4,
∵AB=AC,
∴AC=4,
故答案为4.
16.解:∵四边形ABCD是矩形,
∴OA=OC,∠AEO=∠CFO;
又∵∠AOE=∠COF,
在△AOE和△COF中,
,
∴△AOE≌△COF,
∴S△AOE=S△COF,
∴图中阴影部分的面积就是△BCD的面积.
S△BCDBC×CD2×3=3.
故答案为:3.
17.解:∵直线y=mx﹣3m+2将四边形ABCD分成面积相等的两部分
∴直线必经过矩形的中心对称点O
∵根据矩形中心对称,可知O(5,3),将它代入y=mx﹣3m+2中得:
3=5m﹣3m+2,即m.
18.解:连接AD,
∵∠BAC=90°,且BA=3,AC=4,
∴BC5,
∵DM⊥AB,DN⊥AC,
∴∠DMA=∠DNA=∠BAC=90°,
∴四边形DMAN是矩形,
∴MN=AD,
∴当AD⊥BC时,AD的值最小,
此时,△ABC的面积AB×ACBC×AD,
∴AD,
∴MN的最小值为;
故答案为:.
19.解;设最快x秒,四边形ABPQ成为矩形,由BP=AQ得
3x=20﹣2x.
解得x=4,
故答案为:4.
三.解答题(共6小题,满分53分)
20.(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB,
∵FC=AE,
∴CD﹣FC=AB﹣AE,
即DF=BE,
∴四边形DEBF是平行四边形,
又∵DE⊥AB,
∴∠DEB=90°,
∴平行四边形DEBF是矩形;
(2)解:∵AF平分∠DAB,
∴∠DAF=∠BAF,
∵DC∥AB,
∴∠DFA=∠BAF,
∴∠DFA=∠DAF,
∴AD=DF=10,
在Rt△AED中,由勾股定理得:DE8,
由(1)得:四边形DEBF是矩形,
∴BF=DE=8.
21.(1)证明:∵△AOB为等边三角形,
∴∠BAO=∠AOB=60°,OA=OB,
∵四边形ABCD是平行四边形
∴OB=ODBD,OA=OCAC,
∴BD=AC,
∴ ABCD是矩形;
(2)解:∵ ABCD是矩形,
∴∠BAD=90°,
∵∠ABO=60°,
∴∠ADB=90°﹣60°=30°,
∴ADAB=4.
22.证明:(1)∵点D是AB的中点,
∴AD=BD,
在△ADE和△BDF中,
,
∴△ADE≌△BDF(SAS);
(2)∵AD=BD,DF=DE,
∴四边形AFBE是平行四边形,
∵点D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,
∴∠DEB=∠CBE,
∵∠ABE=∠CBE,
∴∠DEB=∠ABE,
∴DB=DE,
∴AB=EF,
∴平行四边形AFBE是矩形.
23.(1)证明:∵四边形ABDE是平行四边形,
∴AB∥DE,AB=ED,
∵DC=ED,
∴DC=AB,DC∥AB,
∴四边形ABCD是平行四边形,
∵DE⊥AD,
∴∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:过O作OF⊥CD于F,
∵四边形ABCD是矩形,AD=4,AB=2
∴DE=CD=AB=2,AD=BC=4,AC=BD,AO=OC,BO=DO,
∴OD=OC,
∵OF⊥CD,
∴DF=CFCD1,
∴OFBC2,EF=DE+DF=2+1=3,
∴OE.
24.(1)证明:∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠ADC=90°,
∴平行四边形ABCD是矩形;
(2)解:由(1)得:∠ADC=90°,四边形ABCD是矩形,
∵∠ADF:∠FDC=2:1,AC=BD,
∴∠FDC=30°,
∵DF⊥AC,
∴∠DCO=90°﹣30°=60°,
∵AO=CO,BO=DO,
∴OC=OD,
∴∠ODC=∠DCO=60°,
∴∠BDF=∠ODC﹣∠FDC=30°.
25.(1)证明:∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC=90°,
∴∠BAD=90°,
∴∠BAD=∠ABC=∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,DE平分∠ADC,
∴∠CDE=∠CED=45°,
∴EC=DC,
又∵∠BDE=15°,
∴∠CDO=60°,
又∵矩形的对角线互相平分且相等,
∴OD=OC,
∴△OCD是等边三角形,
∴∠DOC=∠OCD=60°,
∴∠OCB=90°﹣∠DCO=30°,
∵CO=CE,
∴∠COE=(180°﹣30°)÷2=75°,
∴∠DOE=∠DOC+∠COE=60°+75°=135°;
(3)解:作OF⊥BC于F.
∵四边形ABCD是矩形,
∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD,
∴AO=BO=CO=DO,
∴BF=FC,
∴OFCD=1,
∵∠OCB=30°,AB=2,
∴BC=2,
∵DE平分∠ADC,∠ADC=90°,
∴∠EDC=45°,
在Rt△EDC中,EC=CD=2,
∴△BOE的面积 EB OF(22)×11.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
