北师大版九年级数学上册1.3正方形的性质与判定知识点分类练习题(含解析)
文档属性
| 名称 | 北师大版九年级数学上册1.3正方形的性质与判定知识点分类练习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 320.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 18:34:19 | ||
图片预览



文档简介
2022-2023学年北师大版九年级数学上册《1.3正方形的性质与判定》
知识点分类练习题(附答案)
一.正方形的性质
1.下列各组图形中,对角线互相平分且相等的是( )
A.矩形与正方形 B.菱形与矩形
C.平行四边形与菱形 D.菱形与正方形
2.菱形、矩形、正方形都具有的性质是( )
A.对角线相等且互相平分 B.对角线相等且互相垂直
C.对角线互相平分 D.四条边相等
3.如图,正方形ABCD中,M、N是对角线BD上的两点,且∠MAN=45°.若BM=2,DN=3,则MN的长为( )
A. B. C.4 D.5
4.如图,在边长为6的正方形ABCD中,E、F分别在边BC、CD上,且∠EAF=45°,连接EF,若BE+DF=5,则△AEF的面积为( )
A.30 B.15 C.11 D.5.5
5.已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合)且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个结论:
①△OEF始终是等腰直角三角形;②△OEF面积的最小值是1;
③至少存在一个△ECF,使得△ECF的周长是2;
④四边形OECF的面积始终是1.
所有正确结论的序号是( )
A.①②③④ B.①②③ C.①③④ D.③④
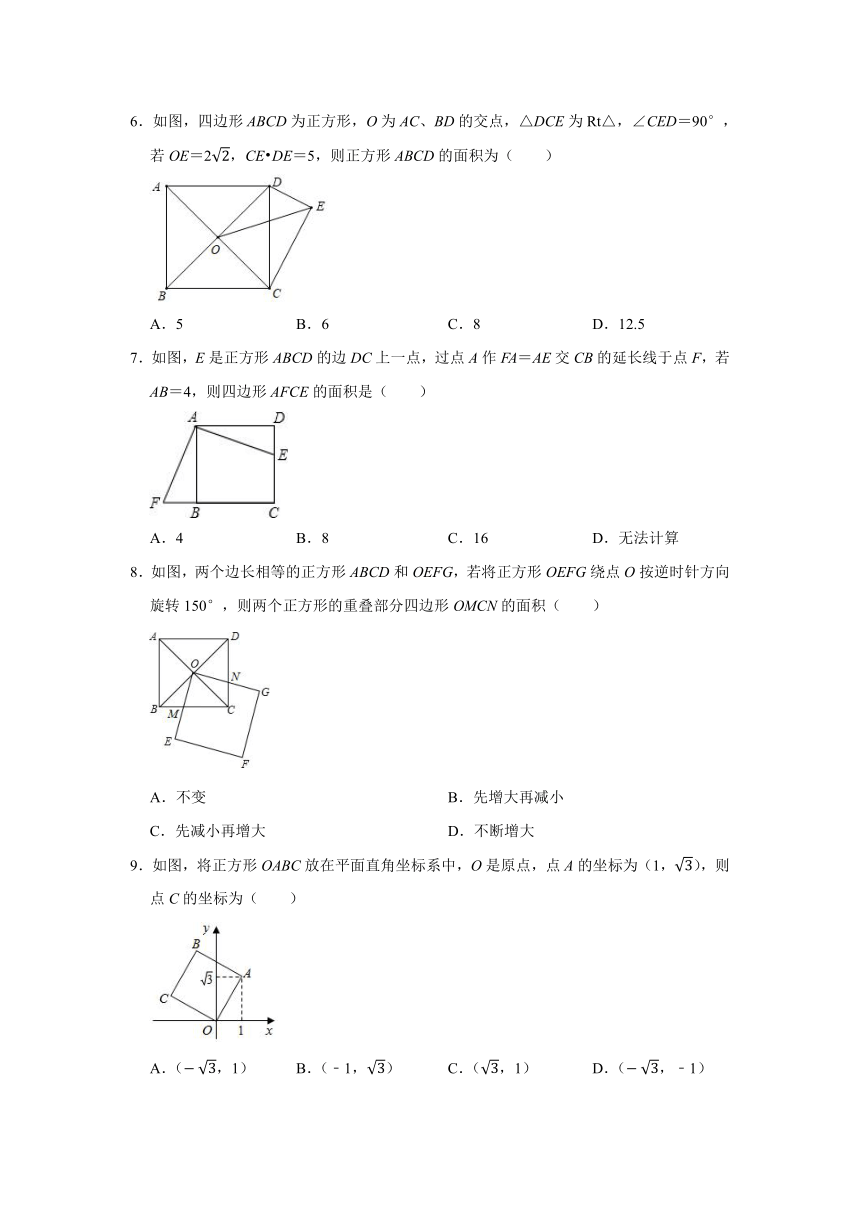
6.如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,若OE=2,CE DE=5,则正方形ABCD的面积为( )
A.5 B.6 C.8 D.12.5
7.如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
A.4 B.8 C.16 D.无法计算
8.如图,两个边长相等的正方形ABCD和OEFG,若将正方形OEFG绕点O按逆时针方向旋转150°,则两个正方形的重叠部分四边形OMCN的面积( )
A.不变 B.先增大再减小
C.先减小再增大 D.不断增大
9.如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,),则点C的坐标为( )
A.(,1) B.(﹣1,) C.(,1) D.(,﹣1)
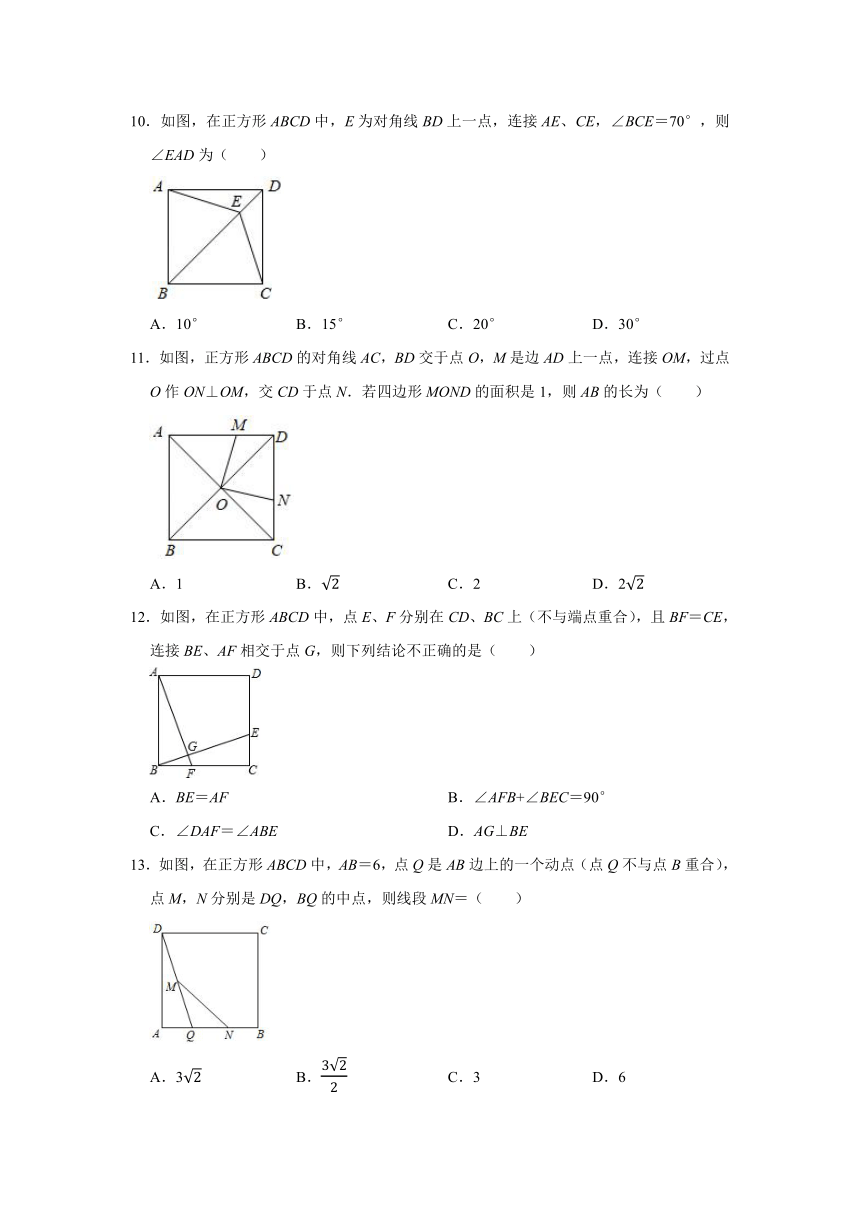
10.如图,在正方形ABCD中,E为对角线BD上一点,连接AE、CE,∠BCE=70°,则∠EAD为( )
A.10° B.15° C.20° D.30°
11.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
12.如图,在正方形ABCD中,点E、F分别在CD、BC上(不与端点重合),且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是( )
A.BE=AF B.∠AFB+∠BEC=90°
C.∠DAF=∠ABE D.AG⊥BE
13.如图,在正方形ABCD中,AB=6,点Q是AB边上的一个动点(点Q不与点B重合),点M,N分别是DQ,BQ的中点,则线段MN=( )
A.3 B. C.3 D.6
14.如图,四边形ABCD是正方形,△CDE是等边三角形,连接AE,则∠AED的度数为( )
A.10° B.15° C.20° D.30°
15.如图,在正方形ABCD中,点P在AC上,PE⊥AB,PF⊥BC,垂足分别为E,F,EF=3,则DP的长为 .
16.如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的度数是 度.
17.两个边长为10cm的正方形按如图所示的方式重叠在一起,点O是其中一个正方形的中心,则重叠部分的面积为 cm2.
18.边长为4的正方形ABCD中,点E、F分别是AB、BC的中点,连结EC、FD,点G,H分别是EC、DF的中点,连结GH,则GH的长为 .
19.如图,两个正方形边长分别为2、a(a>2),图中阴影部分的面积为 .
20.如图,在正方形ABCD中,点E、F分别为边BC、CD上两点,∠EAF=45°,过点A作∠GAB=∠FAD,且点G为边CB延长线上一点.
①△GAB≌△FAD吗?说明理由.
②若线段DF=4,BE=8,求线段EF的长度.
③若DF=4,CF=8.求线段EF的长度.
21.已知四边形ABCD和四边形CEFG都是正方形,且AB>CE,连接BG、DE.
求证:(1)BG=DE;(2)BG⊥DE.
二.正方形的判定
22.如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,连接EF,EF与AD相交于点H.
(1)求证:AD⊥EF;
(2)△ABC满足什么条件时,四边形AEDF是正方形?说明理由.
23.如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P,Q分别从点A,C同时出发,点P以每秒3cm的速度向点B移动,点Q以每秒2cm测得速度向点D移动,当点P到达点B处时,两点均停止移动
(1)P,Q两点出发多长时间,线段PQ的长度为10cm?
(2)是否存在某一时刻,使四边形PBCQ为正方形?若存在,求出该时刻;若不存在,请说明理由.
24.已知:如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)求证:四边形BECF是菱形;
(2)当∠A的大小为多少度时,四边形BECF是正方形?
25.如图,在 ABCD中,AC的垂直平分线分别交BC、AD于点E、F,垂足为O,连接AE、CF.
(1)求证:四边形AECF为菱形;
(2)若AB=5,BC=7,则AC= 时,四边形AECF为正方形.
26.如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E,使AE∥BC,连接AE.
(1)求证:四边形ADCE是矩形;
(2)①若AB=17,BC=16,则四边形ADCE的面积= .
②若AB=10,则BC= 时,四边形ADCE是正方形.
三.正方形的判定与性质
27.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OD的长.
28.如图,已知四边形ABCD为正方形,AB=4,点E为对角线AC上一动点,连接DE、过点E作EF⊥DE.交BC点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
29.如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE、EF为邻边作矩形DEFG,连接AG.
(1)求证:矩形DEFG是正方形;
(2)求AG+AE的值;
(3)若F恰为AB中点,连接DF交AC于点M,请直接写出ME的长.
30.如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE.
(1)求证:BF=DE;
(2)当点E运动到AC中点时(其他条件都保持不变),问四边形AFBE是什么特殊四边形?说明理由.
31.如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.
32.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.
(1)求证:四边形MANP是正方形;
(2)求证:EM=BN.
参考答
一.正方形的性质
1.解:∵矩形的对角线互相平分且相等,菱形的对角线互相平分且垂直,
平行四边形的对角线互相平分,正方形的对角线互相平分且相等且互相垂直,
∴对角线互相平分且相等的是矩形与正方形,
故选:A.
2.解:A、三个图形中,只有矩形和正方形的对角线相等且互相平分,故本选项错误;
B、三个图形中,只有正方形的对角线相等且互相垂直,故本选项错误;
C、平行四边形的对角线互相平分,以上三个图形都是平行四边形,故本选项正确;
D、矩形的四条边不一定相等,故本选项错误;
故选:C.
3.解:将△ABM绕点A逆时针旋转90°得到△ADH,连接NH,
∵∠MAN=45°,
∴∠MAN=∠HAN=45°,
∵△ABM绕点A逆时针旋转90°得到△ADH,
∴AH=AM,BM=DH=2,∠ABM=∠ADH=45°,
又AN=AN,
∴△AMN≌△AHN(SAS),
∴MN=HN,
∵∠NDH=∠ABM+∠ADH=45°+45°=90°,
∴MN=HN.
故选:B.
4.解:延长EB到点H,使得BH=DF,连接AH,如图所示:
在正方形ABCD中,AB=AD,∠ABE=∠D=∠BAD=90°,
∴∠ABH=∠D,
在△ABH和△ADF中,
,
∴△ABH≌△ADF(SAS),
∴∠HAB=∠FAD,AH=AF,
∵∠EAF=45°,
∴∠BAE+∠FAD=45°,
∴∠BAE+∠HAB=45°,
在△HAE和△FAE中,
,
∴△HAE≌△FAE(SAS),
∴EH=EF,
∵BE+DF=5,
∴BE+BH=5,
∴HE=5,
∵AB=6,
∴15,
∴△AEF的面积为15,
故选:B.
5.解:①∵四边形ABCD是正方形,AC,BD相交于点O,
∴OB=OC,∠OBC=∠OCD=45°,
在△OBE和△OCF中,
,
∴△OBE≌△OCF(SAS),
∴OE=OF,
∵∠BOE=∠COF,
∴∠EOF=∠BOC=90°,
∴△OEF是等腰直角三角形;
故①正确;
②∵当OE⊥BC时,OE最小,此时OE=OFBC=1,
∴△OEF面积的最小值是1×1,
故②错误;
③∵BE=CF,
∴CE+CF=CE+BE=BC=2,
假设存在一个△ECF,使得△ECF的周长是2,
则EF,
由①得△OEF是等腰直角三角形,
∴OE.
∵OB,OE的最小值是1,
∴存在一个△ECF,使得△ECF的周长是2.
故③正确;
④由①知:△OBE≌△OCF,
∴S四边形OECF=S△COE+S△OCF=S△COE+S△OBE=S△OBCS正方形ABCD2×2=1,
故④正确;
故选:C.
6.解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵四边形ABCD是正方形,
∵∠COM+∠DOM=90°=∠DON+∠DOM,OC=OD,
∴∠COM=∠DON,
在△COM和△DON中,
,
∴△COM≌△DON(AAS),
∴OM=ON,CM=DN,
∴四边形OMEN是正方形,
在Rt△OEN中,
∵OE=2,
∴2NE2=OE2=(2)2=8,
∴NE=ON=2,
∴DE+CE=DE+EM+MC=DE+EM+DN=EN+EM=2EN=4,
设DE=a,CE=b,
∴a+b=4,
∵CE DE=5,
∴CD2=a2+b2=(a+b)2﹣2ab=42﹣2×5=6,
∴S正方形ABCD=6,
故选:B.
7.解:∵四边形ABCD是正方形,
∴∠ABC=∠D=90°,AB=AD,
即∠ABF=∠D=90°,
在Rt△ABF和Rt△ADE中,
,
∴Rt△ABF≌Rt△ADE(HL),
∴SRt△ABF=SRt△ADE,
∴SRt△ABF+S四边形ABCE=SRt△ADE+S四边形ABCE,
∴S四边形AFCE=S正方形ABCD=16.
故选:C.
8.解:∵四边形ABCD、四边形PEFG是两个边长相等正方形,
∴∠BOC=∠EOG=90°,∠OBC=∠OCD=45°,OB=OC,
∴∠BOC﹣∠COM=∠EOG﹣∠COM,
即∠BOM=∠CON,
∵在△BOM和△CON中
,
∴△BOM≌△CON,
∴两个正方形的重叠部分四边形OMCN的面积是S△COM+S△CNO=S△COM+S△BOM=S△BOCS正方形ABCD,
即不管怎样移动,阴影部分的面积都等于S正方形ABCD,
故选:A.
9.解:如图所示,作AD⊥x轴于D,CE⊥x轴于E,则∠OEC=∠ADO=90°,
∴∠1+∠2=90°,
∵A的坐标为(1,),
∴AD,OD=1,
∵四边形OABC是正方形,
∴OA=OC,∠AOC=90°,
∴∠1+∠3=90°,
∴∠3=∠2,
在△OCE和△AOD中,
,
∴△OCE≌△AOD(AAS),
∴OE=AD,CE=OD=1,
∴C(,1).
故选:A.
10.解:∵正方形ABCD,
∴∠ADE=∠CDE=∠EBC=45°,AD=CD,
∵DE=DE,
∴△AED≌△CED(SAS),
∴∠EAD=∠ECD,
又∵∠BCE=70°,
∴∠BEC=65°,
∵∠BEC=∠CDE+∠ECD,
即65°=45°+∠ECD,
∴∠ECD=20°,
∴∠EAD=20°.
故选:C.
11.解:∵四边形ABCD是正方形,
∴∠MDO=∠NCO=45°,OD=OC,∠DOC=90°,
∴∠DON+∠CON=90°,
∵ON⊥OM,
∴∠MON=90°,
∴∠DON+∠DOM=90°,
∴∠DOM=∠CON,
在△DOM和△CON中,
,
∴△DOM≌△CON(ASA),
∵四边形MOND的面积是1,四边形MOND的面积=△DOM的面积+△DON的面积,
∴四边形MOND的面积=△CON的面积+△DON的面积=△DOC的面积,
∴△DOC的面积是1,
∴正方形ABCD的面积是4,
∴AB2=4,
∴AB=2,
故选:C.
12.解:∵四边形ABCD是正方形,
∴∠ABF=∠C=90°,AB=BC,
∵BF=CE,
∴△ABF≌△BCE(SAS),
∴AF=BE(A正确),∠BAF=∠CBE,∠AFB=∠BEC(B错误),
∵∠BAF+∠DAF=90°,∠ABE+∠EBC=90°,
∴∠DAF=∠ABE(C正确),
∵∠BAF=∠CBE,∠BAF+∠AFB=90°,
∴∠CBE+∠AFB=90°,
∴AG⊥BE(D正确),
所以不正确的是B,
故选:B.
13.解:连接DB,
∵四边形ABCD是正方形,AB=6,
∴∠A=90°,AD=AB=6,
∴DB6,
∵点M,N分别是DQ,BQ的中点,
∴MN是△DQB的中位线,
∴MNDB=3,
故选:A.
14.解:∵四边形ABCD是正方形,
∴DA=DC,∠ADC=90°,
∵△CDE是等边三角形,
∴DC=DE,∠CDE=60°,
∴DA=DE,∠ADE=150°,
∴∠DAE=∠DEA(180°﹣150°)=15°.
故选:B.
15.解:如图,连接PB,
在正方形ABCD中,AB=AD,∠BAC=∠DAC=45°,
∵AP=AP,AB=AD,∠BAC=∠DAC=45°,
在△ABP和△ADP中,
,
∴△ABP≌△ADP(SAS),
∴BP=DP;
∵PE⊥AB,PF⊥BC,∠ABC=90°,
∴四边形BFPE是矩形,
∴EF=PB,
∴EF=DP=3,
故答案为:3.
16.解:∵四边形ABCD是正方形,
∴AB=BC=AD=CD,∠ABC=90°,∠ADG=∠CDG,∠ABD=45°,
∵GD=GD,
∴△ADG≌△CDG,
∴∠AGD=∠CGD,
∵∠CGD=∠EGB,
∴∠AGD=∠EGB,
∵△ABE是等边三角形,
∴AB=BE,∠ABE=60°,
∴BE=BC,∠EBC=150°,
∴∠BEC=∠ECB=15°,
∴∠BGE=180°﹣∠BEC﹣∠EBG=180°﹣15°﹣60°﹣45°=60°,
∴∠AGD=60°
故答案为60.
17.解:如图,连接OA、OD,则∠AOD=∠GOE=90°,
∴∠AOM=∠DON,
∵ABCD是正方形,O为正方形ABCD的中心,
∴OA=OD,∠OAM=∠ODN=45°,
在△OAM和△ODN中,,
∴△OAM≌△ODN(ASA),
∴S△OAM=S△ODN,
∴S阴影=S△ODM+S△ODN=S△OAM+S△ODM=S△OAD,
S正方形ABCD102=25(cm2),
故答案是:25.
18.解:连接CH并延长交AD于P,连接PE,
∵四边形ABCD是正方形,
∴∠A=90°,AD∥BC,AB=AD=BC=4,
∵E,F分别是边AB,BC的中点,
∴AE=CF,
∵AD∥BC,
∴∠DPH=∠FCH,
在△PDH和△CFH中,
,
∴△PDH≌△CFH(AAS),
∴PD=CF=2,
∴AP=AD﹣PD=2,
∴PE,
∵点G,H分别是EC,FD的中点,
∴GHEP.
19.解:阴影部分的面积
20.解:①全等.
证明:∵四边形ABCD为正方形
∴AB=AD,∠ABG=∠D,
在△ABG和△ADF中,∠GAB=∠FAD,AB=AD,∠ABG=∠D
∴△GAB≌△FAD.
②解:∵∠BAD=90°,∠EAF=45°
∴∠DAF+∠BAE=45°
∵△GAB≌△FAD
∴∠GAB=∠FAD,AG=AF
∴∠GAB+∠BAE=45°
∴∠GAE=45°
∴∠GAE=∠EAF
在△GAE和△FAE中
∵AG=AF,∠GAE=∠EAF,AE=AE
∴△GAE≌△FAE(SAS)
∴EF=GE.
∵△GAB≌△FAD
∴GB=DF
∴EF=GE=GB+BE=FD+BE=8+4=12.
③设EF=x,则BE=GE﹣BG=x﹣4.
∵EC=BC﹣BE,
∴EC=12﹣(x﹣4)=16﹣x.
在Rt△EFC中,依据勾股定理可知:EF2=FC2+EC2,即(16﹣x)2+82=x2,
解得:x=10.
∴EF=10.
21.证明:(1)∵四边形ABCD和CEFG为正方形,
∴BC=DC,CG=CE,∠BCD=∠GCE=90°,
∴∠BCD+∠DCG=∠GCE+∠DCG,
即:∠BCG=∠DCE,
在△BCG和△DCE中,,
∴△BCG≌△DCE(SAS),
∴BG=DE,
(2)∵△BCG≌△DCE,
∴∠GBC=∠EDC,
∵∠GBC+∠BOC=90°,∠BOC=∠DOG,
∴∠DOG+∠EDC=90°,
∴BG⊥DE.
二.正方形的判定
22.(1)证明:∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在△AED与△AFD中,
,
∴△AED≌△AFD(AAS),
∴AE=AF,
∴AD⊥EF;
(2)解:△ABC满足∠BAC=90°时,四边形AEDF是正方形,
理由:∵∠AED=∠AFD=∠BAC=90°,
∴四边形AEDF是矩形,
∵EF⊥AD,
∴矩形AEDF是正方形.
23.解:(1)过点P作PH⊥CD于点H,
∴HQ=16﹣5t,
∴PQ2=PH2+HQ2,
即102=(16﹣5t)2+62,
解得:,
答:P,Q两点出发或秒,线段PQ的长度为10cm;
(2)假设四边形PBCQ是正方形,
∴BP=CQ,即16﹣3t=2t,
解得:t,
∵,
∴不成立.
24.解:(1)∵EF垂直平分BC,
∴CF=BF,BE=CE,∠BDE=90°,BD=CD,
又∵∠ACB=90°,
∴EF∥AC,
∵D为BC中点,
∴DB:BC=1:2,
∴BE:AB=1:2,
∴E为AB中点,
即BE=AE,
∵CF=AE,
∴CF=BE,
∴CF=FB=BE=CE,
∴四边形BECF是菱形.
(2)当∠A=45°时,四边形BECF是正方形.
证明:∵∠A=45°,∠ACB=90°,
∴∠CBA=45°,
∴∠EBF=2∠CBA=90°,
∴菱形BECF是正方形.
25.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠FAC=∠ECA,
∵EF垂直平分AC,
∴AF=CF,AE=CE,
∴∠FAC=∠ACF,∠ACE=∠EAC
∴∠EAC=∠ACF,
∴AE∥CF,
∴四边形AECF是平行四边形,
又∵AF=CF,
∴四边形AECF是菱形;
(2)若四边形AECF为正方形,
∴AE=EC,∠AEC=∠AEB=90°,ACAE,
∵AB2=BE2+AE2,
∴25=(7﹣AE)2+AE2,
∴AE=3或4,
∴AC=3或4,
故答案为:3或4.
26.(1)证明:∵点O是AC中点,
∴AO=OC,
∵AE∥BC,
∴∠AEO=∠ODC,∠EAO=∠OCD,
∴△AOE≌△COD(AAS),
∴OE=OD,
∴四边形ADCE是平行四边形,
∵AD是等腰△ABC底边BC上的高,
∴∠ADC=90°,
∴四边形ADCE是矩形;
(2)①∵AD是等腰△ABC底边BC上的高,BC=16,AB=17,
∴BD=CD=8,AB=AC=17,∠ADC=90°,
由勾股定理得:AD15,
∴四边形ADCE的面积是AD×DC=15×8=120.
②当AB=10,BC=10时,四边形ADCE是正方形,理由如下:
∵AB=AC=10,BC=10,
∴ADDC,
∵AD⊥BC,
∴四边形ADCE是正方形;
故答案为:120;10.
三.正方形的判定与性质
27.(1)证明:∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,∠BAE=∠DAG=45°,
∴四边形ABEF是正方形;
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∴AD,∠DAG=∠ADG=45°,
∴DF1,
∵EF⊥AD,
∴∠FDO=∠FOD=45°,
∴DF=FO1,
∴DODF=2.
28.解:(1)如图所示,过E作EM⊥BC于M点,过E作EN⊥CD于N点,
∵正方形ABCD,
∴∠BCD=90°,∠ECN=45°,
∴∠EMC=∠ENC=∠BCD=90°,且NE=NC,
∴四边形EMCN为正方形,
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°,
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形,
(2)CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°,
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴AC=AE+CEAB48,
∴CE+CG=8是定值.
29.解:(1)如图,作EM⊥AD于M,EN⊥AB于N.
∵四边形ABCD是正方形,
∴∠EAD=∠EAB,
∵EM⊥AD于M,EN⊥AB于N,
∴EM=EN,
∵∠EMA=∠ENA=∠DAB=90°,
∴四边形ANEM是矩形,
∵EF⊥DE,
∴∠MEN=∠DEF=90°,
∴∠DEM=∠FEN,
∵∠EMD=∠ENF=90°,
∴△EMD≌△ENF,
∴ED=EF,
∵四边形DEFG是矩形,
∴四边形DEFG是正方形.
(2)∵四边形DEFG是正方形,四边形ABCD是正方形,
∴DG=DE,DC=DA=AB=4,∠GDE=∠ADC=90°,
∴∠ADG=∠CDE,
∴△ADG≌△CDE(SAS),
∴AG=CE,
∴AE+AG=AE+EC=ACAD=4.
(3)如图,作EH⊥DF于H.
∵四边形ABCD是正方形,
∴AB=AD=4,AB∥CD,
∵F是AB中点,
∴AF=FB
∴DF2,
∵△DEF是等腰直角三角形,EH⊥DF,
∴DH=HF,
∴EHDF,
∵AF∥CD,
∴AF:CD=FM:MD=1:2,
∴FM,
∴HM=HF﹣FM,
在Rt△EHM中,EM.
30.(1)证明:∵正方形ABCD,
∴AB=AD,∠BAD=90°,
∵AF⊥AC,
∴∠EAF=90°,
∴∠BAF=∠EAD,
在△ADE和△ABF中
∴△ADE≌△ABF(SAS),
∴BF=DE;
(2)解:当点E运动到AC的中点时四边形AFBE是正方形,
理由:∵点E运动到AC的中点,AB=BC,
∴BE⊥AC,BE=AEAC,
∵AF=AE,
∴BE=AF=AE,
又∵BE⊥AC,∠FAE=∠BEC=90°,
∴BE∥AF,
∵BE=AF,
∴得平行四边形AFBE,
∵∠FAE=90°,AF=AE,
∴四边形AFBE是正方形.
31.证明:(1)连接GE,
∵AB∥CD,
∴∠AEG=∠CGE,
∵GF∥HE,
∴∠HEG=∠FGE,
∴∠HEA=∠CGF;
(2)∵四边形ABCD是正方形,
∴∠D=∠A=90°,
∵四边形EFGH是菱形,
∴HG=HE,
在Rt△HAE和Rt△GDH中,
,
∴Rt△HAE≌Rt△GDH(HL),
∴∠AHE=∠DGH,又∠DHG+∠DGH=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∴菱形EFGH为正方形;
32.证明:(1)∵四边形ABCD是正方形,
∴∠DAB=90°,AC平分∠DAB,
∵PM⊥AD,PN⊥AB,
∴∠PMA=∠PNA=90°,
∴四边形MANP是矩形,
∵AC平分∠DAB,PM⊥AD,PN⊥AB,
∴PM=PN,
∴四边形MANP是正方形;
(2)∵四边形ABCD是正方形,
∴PM=PN,∠MPN=90°,
∵∠EPB=90°,
∴∠MPE+∠EPN=∠NPB+∠EPN=90°,
∴∠MPE=∠NPB,
在△EPM和△BPN中,
∵,
∴△EPM≌△BPN(ASA),
∴EM=BN.
知识点分类练习题(附答案)
一.正方形的性质
1.下列各组图形中,对角线互相平分且相等的是( )
A.矩形与正方形 B.菱形与矩形
C.平行四边形与菱形 D.菱形与正方形
2.菱形、矩形、正方形都具有的性质是( )
A.对角线相等且互相平分 B.对角线相等且互相垂直
C.对角线互相平分 D.四条边相等
3.如图,正方形ABCD中,M、N是对角线BD上的两点,且∠MAN=45°.若BM=2,DN=3,则MN的长为( )
A. B. C.4 D.5
4.如图,在边长为6的正方形ABCD中,E、F分别在边BC、CD上,且∠EAF=45°,连接EF,若BE+DF=5,则△AEF的面积为( )
A.30 B.15 C.11 D.5.5
5.已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合)且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个结论:
①△OEF始终是等腰直角三角形;②△OEF面积的最小值是1;
③至少存在一个△ECF,使得△ECF的周长是2;
④四边形OECF的面积始终是1.
所有正确结论的序号是( )
A.①②③④ B.①②③ C.①③④ D.③④
6.如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,若OE=2,CE DE=5,则正方形ABCD的面积为( )
A.5 B.6 C.8 D.12.5
7.如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
A.4 B.8 C.16 D.无法计算
8.如图,两个边长相等的正方形ABCD和OEFG,若将正方形OEFG绕点O按逆时针方向旋转150°,则两个正方形的重叠部分四边形OMCN的面积( )
A.不变 B.先增大再减小
C.先减小再增大 D.不断增大
9.如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,),则点C的坐标为( )
A.(,1) B.(﹣1,) C.(,1) D.(,﹣1)
10.如图,在正方形ABCD中,E为对角线BD上一点,连接AE、CE,∠BCE=70°,则∠EAD为( )
A.10° B.15° C.20° D.30°
11.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
12.如图,在正方形ABCD中,点E、F分别在CD、BC上(不与端点重合),且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是( )
A.BE=AF B.∠AFB+∠BEC=90°
C.∠DAF=∠ABE D.AG⊥BE
13.如图,在正方形ABCD中,AB=6,点Q是AB边上的一个动点(点Q不与点B重合),点M,N分别是DQ,BQ的中点,则线段MN=( )
A.3 B. C.3 D.6
14.如图,四边形ABCD是正方形,△CDE是等边三角形,连接AE,则∠AED的度数为( )
A.10° B.15° C.20° D.30°
15.如图,在正方形ABCD中,点P在AC上,PE⊥AB,PF⊥BC,垂足分别为E,F,EF=3,则DP的长为 .
16.如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的度数是 度.
17.两个边长为10cm的正方形按如图所示的方式重叠在一起,点O是其中一个正方形的中心,则重叠部分的面积为 cm2.
18.边长为4的正方形ABCD中,点E、F分别是AB、BC的中点,连结EC、FD,点G,H分别是EC、DF的中点,连结GH,则GH的长为 .
19.如图,两个正方形边长分别为2、a(a>2),图中阴影部分的面积为 .
20.如图,在正方形ABCD中,点E、F分别为边BC、CD上两点,∠EAF=45°,过点A作∠GAB=∠FAD,且点G为边CB延长线上一点.
①△GAB≌△FAD吗?说明理由.
②若线段DF=4,BE=8,求线段EF的长度.
③若DF=4,CF=8.求线段EF的长度.
21.已知四边形ABCD和四边形CEFG都是正方形,且AB>CE,连接BG、DE.
求证:(1)BG=DE;(2)BG⊥DE.
二.正方形的判定
22.如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,连接EF,EF与AD相交于点H.
(1)求证:AD⊥EF;
(2)△ABC满足什么条件时,四边形AEDF是正方形?说明理由.
23.如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P,Q分别从点A,C同时出发,点P以每秒3cm的速度向点B移动,点Q以每秒2cm测得速度向点D移动,当点P到达点B处时,两点均停止移动
(1)P,Q两点出发多长时间,线段PQ的长度为10cm?
(2)是否存在某一时刻,使四边形PBCQ为正方形?若存在,求出该时刻;若不存在,请说明理由.
24.已知:如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)求证:四边形BECF是菱形;
(2)当∠A的大小为多少度时,四边形BECF是正方形?
25.如图,在 ABCD中,AC的垂直平分线分别交BC、AD于点E、F,垂足为O,连接AE、CF.
(1)求证:四边形AECF为菱形;
(2)若AB=5,BC=7,则AC= 时,四边形AECF为正方形.
26.如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E,使AE∥BC,连接AE.
(1)求证:四边形ADCE是矩形;
(2)①若AB=17,BC=16,则四边形ADCE的面积= .
②若AB=10,则BC= 时,四边形ADCE是正方形.
三.正方形的判定与性质
27.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OD的长.
28.如图,已知四边形ABCD为正方形,AB=4,点E为对角线AC上一动点,连接DE、过点E作EF⊥DE.交BC点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
29.如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE、EF为邻边作矩形DEFG,连接AG.
(1)求证:矩形DEFG是正方形;
(2)求AG+AE的值;
(3)若F恰为AB中点,连接DF交AC于点M,请直接写出ME的长.
30.如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE.
(1)求证:BF=DE;
(2)当点E运动到AC中点时(其他条件都保持不变),问四边形AFBE是什么特殊四边形?说明理由.
31.如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.
32.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.
(1)求证:四边形MANP是正方形;
(2)求证:EM=BN.
参考答
一.正方形的性质
1.解:∵矩形的对角线互相平分且相等,菱形的对角线互相平分且垂直,
平行四边形的对角线互相平分,正方形的对角线互相平分且相等且互相垂直,
∴对角线互相平分且相等的是矩形与正方形,
故选:A.
2.解:A、三个图形中,只有矩形和正方形的对角线相等且互相平分,故本选项错误;
B、三个图形中,只有正方形的对角线相等且互相垂直,故本选项错误;
C、平行四边形的对角线互相平分,以上三个图形都是平行四边形,故本选项正确;
D、矩形的四条边不一定相等,故本选项错误;
故选:C.
3.解:将△ABM绕点A逆时针旋转90°得到△ADH,连接NH,
∵∠MAN=45°,
∴∠MAN=∠HAN=45°,
∵△ABM绕点A逆时针旋转90°得到△ADH,
∴AH=AM,BM=DH=2,∠ABM=∠ADH=45°,
又AN=AN,
∴△AMN≌△AHN(SAS),
∴MN=HN,
∵∠NDH=∠ABM+∠ADH=45°+45°=90°,
∴MN=HN.
故选:B.
4.解:延长EB到点H,使得BH=DF,连接AH,如图所示:
在正方形ABCD中,AB=AD,∠ABE=∠D=∠BAD=90°,
∴∠ABH=∠D,
在△ABH和△ADF中,
,
∴△ABH≌△ADF(SAS),
∴∠HAB=∠FAD,AH=AF,
∵∠EAF=45°,
∴∠BAE+∠FAD=45°,
∴∠BAE+∠HAB=45°,
在△HAE和△FAE中,
,
∴△HAE≌△FAE(SAS),
∴EH=EF,
∵BE+DF=5,
∴BE+BH=5,
∴HE=5,
∵AB=6,
∴15,
∴△AEF的面积为15,
故选:B.
5.解:①∵四边形ABCD是正方形,AC,BD相交于点O,
∴OB=OC,∠OBC=∠OCD=45°,
在△OBE和△OCF中,
,
∴△OBE≌△OCF(SAS),
∴OE=OF,
∵∠BOE=∠COF,
∴∠EOF=∠BOC=90°,
∴△OEF是等腰直角三角形;
故①正确;
②∵当OE⊥BC时,OE最小,此时OE=OFBC=1,
∴△OEF面积的最小值是1×1,
故②错误;
③∵BE=CF,
∴CE+CF=CE+BE=BC=2,
假设存在一个△ECF,使得△ECF的周长是2,
则EF,
由①得△OEF是等腰直角三角形,
∴OE.
∵OB,OE的最小值是1,
∴存在一个△ECF,使得△ECF的周长是2.
故③正确;
④由①知:△OBE≌△OCF,
∴S四边形OECF=S△COE+S△OCF=S△COE+S△OBE=S△OBCS正方形ABCD2×2=1,
故④正确;
故选:C.
6.解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵四边形ABCD是正方形,
∵∠COM+∠DOM=90°=∠DON+∠DOM,OC=OD,
∴∠COM=∠DON,
在△COM和△DON中,
,
∴△COM≌△DON(AAS),
∴OM=ON,CM=DN,
∴四边形OMEN是正方形,
在Rt△OEN中,
∵OE=2,
∴2NE2=OE2=(2)2=8,
∴NE=ON=2,
∴DE+CE=DE+EM+MC=DE+EM+DN=EN+EM=2EN=4,
设DE=a,CE=b,
∴a+b=4,
∵CE DE=5,
∴CD2=a2+b2=(a+b)2﹣2ab=42﹣2×5=6,
∴S正方形ABCD=6,
故选:B.
7.解:∵四边形ABCD是正方形,
∴∠ABC=∠D=90°,AB=AD,
即∠ABF=∠D=90°,
在Rt△ABF和Rt△ADE中,
,
∴Rt△ABF≌Rt△ADE(HL),
∴SRt△ABF=SRt△ADE,
∴SRt△ABF+S四边形ABCE=SRt△ADE+S四边形ABCE,
∴S四边形AFCE=S正方形ABCD=16.
故选:C.
8.解:∵四边形ABCD、四边形PEFG是两个边长相等正方形,
∴∠BOC=∠EOG=90°,∠OBC=∠OCD=45°,OB=OC,
∴∠BOC﹣∠COM=∠EOG﹣∠COM,
即∠BOM=∠CON,
∵在△BOM和△CON中
,
∴△BOM≌△CON,
∴两个正方形的重叠部分四边形OMCN的面积是S△COM+S△CNO=S△COM+S△BOM=S△BOCS正方形ABCD,
即不管怎样移动,阴影部分的面积都等于S正方形ABCD,
故选:A.
9.解:如图所示,作AD⊥x轴于D,CE⊥x轴于E,则∠OEC=∠ADO=90°,
∴∠1+∠2=90°,
∵A的坐标为(1,),
∴AD,OD=1,
∵四边形OABC是正方形,
∴OA=OC,∠AOC=90°,
∴∠1+∠3=90°,
∴∠3=∠2,
在△OCE和△AOD中,
,
∴△OCE≌△AOD(AAS),
∴OE=AD,CE=OD=1,
∴C(,1).
故选:A.
10.解:∵正方形ABCD,
∴∠ADE=∠CDE=∠EBC=45°,AD=CD,
∵DE=DE,
∴△AED≌△CED(SAS),
∴∠EAD=∠ECD,
又∵∠BCE=70°,
∴∠BEC=65°,
∵∠BEC=∠CDE+∠ECD,
即65°=45°+∠ECD,
∴∠ECD=20°,
∴∠EAD=20°.
故选:C.
11.解:∵四边形ABCD是正方形,
∴∠MDO=∠NCO=45°,OD=OC,∠DOC=90°,
∴∠DON+∠CON=90°,
∵ON⊥OM,
∴∠MON=90°,
∴∠DON+∠DOM=90°,
∴∠DOM=∠CON,
在△DOM和△CON中,
,
∴△DOM≌△CON(ASA),
∵四边形MOND的面积是1,四边形MOND的面积=△DOM的面积+△DON的面积,
∴四边形MOND的面积=△CON的面积+△DON的面积=△DOC的面积,
∴△DOC的面积是1,
∴正方形ABCD的面积是4,
∴AB2=4,
∴AB=2,
故选:C.
12.解:∵四边形ABCD是正方形,
∴∠ABF=∠C=90°,AB=BC,
∵BF=CE,
∴△ABF≌△BCE(SAS),
∴AF=BE(A正确),∠BAF=∠CBE,∠AFB=∠BEC(B错误),
∵∠BAF+∠DAF=90°,∠ABE+∠EBC=90°,
∴∠DAF=∠ABE(C正确),
∵∠BAF=∠CBE,∠BAF+∠AFB=90°,
∴∠CBE+∠AFB=90°,
∴AG⊥BE(D正确),
所以不正确的是B,
故选:B.
13.解:连接DB,
∵四边形ABCD是正方形,AB=6,
∴∠A=90°,AD=AB=6,
∴DB6,
∵点M,N分别是DQ,BQ的中点,
∴MN是△DQB的中位线,
∴MNDB=3,
故选:A.
14.解:∵四边形ABCD是正方形,
∴DA=DC,∠ADC=90°,
∵△CDE是等边三角形,
∴DC=DE,∠CDE=60°,
∴DA=DE,∠ADE=150°,
∴∠DAE=∠DEA(180°﹣150°)=15°.
故选:B.
15.解:如图,连接PB,
在正方形ABCD中,AB=AD,∠BAC=∠DAC=45°,
∵AP=AP,AB=AD,∠BAC=∠DAC=45°,
在△ABP和△ADP中,
,
∴△ABP≌△ADP(SAS),
∴BP=DP;
∵PE⊥AB,PF⊥BC,∠ABC=90°,
∴四边形BFPE是矩形,
∴EF=PB,
∴EF=DP=3,
故答案为:3.
16.解:∵四边形ABCD是正方形,
∴AB=BC=AD=CD,∠ABC=90°,∠ADG=∠CDG,∠ABD=45°,
∵GD=GD,
∴△ADG≌△CDG,
∴∠AGD=∠CGD,
∵∠CGD=∠EGB,
∴∠AGD=∠EGB,
∵△ABE是等边三角形,
∴AB=BE,∠ABE=60°,
∴BE=BC,∠EBC=150°,
∴∠BEC=∠ECB=15°,
∴∠BGE=180°﹣∠BEC﹣∠EBG=180°﹣15°﹣60°﹣45°=60°,
∴∠AGD=60°
故答案为60.
17.解:如图,连接OA、OD,则∠AOD=∠GOE=90°,
∴∠AOM=∠DON,
∵ABCD是正方形,O为正方形ABCD的中心,
∴OA=OD,∠OAM=∠ODN=45°,
在△OAM和△ODN中,,
∴△OAM≌△ODN(ASA),
∴S△OAM=S△ODN,
∴S阴影=S△ODM+S△ODN=S△OAM+S△ODM=S△OAD,
S正方形ABCD102=25(cm2),
故答案是:25.
18.解:连接CH并延长交AD于P,连接PE,
∵四边形ABCD是正方形,
∴∠A=90°,AD∥BC,AB=AD=BC=4,
∵E,F分别是边AB,BC的中点,
∴AE=CF,
∵AD∥BC,
∴∠DPH=∠FCH,
在△PDH和△CFH中,
,
∴△PDH≌△CFH(AAS),
∴PD=CF=2,
∴AP=AD﹣PD=2,
∴PE,
∵点G,H分别是EC,FD的中点,
∴GHEP.
19.解:阴影部分的面积
20.解:①全等.
证明:∵四边形ABCD为正方形
∴AB=AD,∠ABG=∠D,
在△ABG和△ADF中,∠GAB=∠FAD,AB=AD,∠ABG=∠D
∴△GAB≌△FAD.
②解:∵∠BAD=90°,∠EAF=45°
∴∠DAF+∠BAE=45°
∵△GAB≌△FAD
∴∠GAB=∠FAD,AG=AF
∴∠GAB+∠BAE=45°
∴∠GAE=45°
∴∠GAE=∠EAF
在△GAE和△FAE中
∵AG=AF,∠GAE=∠EAF,AE=AE
∴△GAE≌△FAE(SAS)
∴EF=GE.
∵△GAB≌△FAD
∴GB=DF
∴EF=GE=GB+BE=FD+BE=8+4=12.
③设EF=x,则BE=GE﹣BG=x﹣4.
∵EC=BC﹣BE,
∴EC=12﹣(x﹣4)=16﹣x.
在Rt△EFC中,依据勾股定理可知:EF2=FC2+EC2,即(16﹣x)2+82=x2,
解得:x=10.
∴EF=10.
21.证明:(1)∵四边形ABCD和CEFG为正方形,
∴BC=DC,CG=CE,∠BCD=∠GCE=90°,
∴∠BCD+∠DCG=∠GCE+∠DCG,
即:∠BCG=∠DCE,
在△BCG和△DCE中,,
∴△BCG≌△DCE(SAS),
∴BG=DE,
(2)∵△BCG≌△DCE,
∴∠GBC=∠EDC,
∵∠GBC+∠BOC=90°,∠BOC=∠DOG,
∴∠DOG+∠EDC=90°,
∴BG⊥DE.
二.正方形的判定
22.(1)证明:∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在△AED与△AFD中,
,
∴△AED≌△AFD(AAS),
∴AE=AF,
∴AD⊥EF;
(2)解:△ABC满足∠BAC=90°时,四边形AEDF是正方形,
理由:∵∠AED=∠AFD=∠BAC=90°,
∴四边形AEDF是矩形,
∵EF⊥AD,
∴矩形AEDF是正方形.
23.解:(1)过点P作PH⊥CD于点H,
∴HQ=16﹣5t,
∴PQ2=PH2+HQ2,
即102=(16﹣5t)2+62,
解得:,
答:P,Q两点出发或秒,线段PQ的长度为10cm;
(2)假设四边形PBCQ是正方形,
∴BP=CQ,即16﹣3t=2t,
解得:t,
∵,
∴不成立.
24.解:(1)∵EF垂直平分BC,
∴CF=BF,BE=CE,∠BDE=90°,BD=CD,
又∵∠ACB=90°,
∴EF∥AC,
∵D为BC中点,
∴DB:BC=1:2,
∴BE:AB=1:2,
∴E为AB中点,
即BE=AE,
∵CF=AE,
∴CF=BE,
∴CF=FB=BE=CE,
∴四边形BECF是菱形.
(2)当∠A=45°时,四边形BECF是正方形.
证明:∵∠A=45°,∠ACB=90°,
∴∠CBA=45°,
∴∠EBF=2∠CBA=90°,
∴菱形BECF是正方形.
25.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠FAC=∠ECA,
∵EF垂直平分AC,
∴AF=CF,AE=CE,
∴∠FAC=∠ACF,∠ACE=∠EAC
∴∠EAC=∠ACF,
∴AE∥CF,
∴四边形AECF是平行四边形,
又∵AF=CF,
∴四边形AECF是菱形;
(2)若四边形AECF为正方形,
∴AE=EC,∠AEC=∠AEB=90°,ACAE,
∵AB2=BE2+AE2,
∴25=(7﹣AE)2+AE2,
∴AE=3或4,
∴AC=3或4,
故答案为:3或4.
26.(1)证明:∵点O是AC中点,
∴AO=OC,
∵AE∥BC,
∴∠AEO=∠ODC,∠EAO=∠OCD,
∴△AOE≌△COD(AAS),
∴OE=OD,
∴四边形ADCE是平行四边形,
∵AD是等腰△ABC底边BC上的高,
∴∠ADC=90°,
∴四边形ADCE是矩形;
(2)①∵AD是等腰△ABC底边BC上的高,BC=16,AB=17,
∴BD=CD=8,AB=AC=17,∠ADC=90°,
由勾股定理得:AD15,
∴四边形ADCE的面积是AD×DC=15×8=120.
②当AB=10,BC=10时,四边形ADCE是正方形,理由如下:
∵AB=AC=10,BC=10,
∴ADDC,
∵AD⊥BC,
∴四边形ADCE是正方形;
故答案为:120;10.
三.正方形的判定与性质
27.(1)证明:∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,∠BAE=∠DAG=45°,
∴四边形ABEF是正方形;
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∴AD,∠DAG=∠ADG=45°,
∴DF1,
∵EF⊥AD,
∴∠FDO=∠FOD=45°,
∴DF=FO1,
∴DODF=2.
28.解:(1)如图所示,过E作EM⊥BC于M点,过E作EN⊥CD于N点,
∵正方形ABCD,
∴∠BCD=90°,∠ECN=45°,
∴∠EMC=∠ENC=∠BCD=90°,且NE=NC,
∴四边形EMCN为正方形,
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°,
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形,
(2)CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°,
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴AC=AE+CEAB48,
∴CE+CG=8是定值.
29.解:(1)如图,作EM⊥AD于M,EN⊥AB于N.
∵四边形ABCD是正方形,
∴∠EAD=∠EAB,
∵EM⊥AD于M,EN⊥AB于N,
∴EM=EN,
∵∠EMA=∠ENA=∠DAB=90°,
∴四边形ANEM是矩形,
∵EF⊥DE,
∴∠MEN=∠DEF=90°,
∴∠DEM=∠FEN,
∵∠EMD=∠ENF=90°,
∴△EMD≌△ENF,
∴ED=EF,
∵四边形DEFG是矩形,
∴四边形DEFG是正方形.
(2)∵四边形DEFG是正方形,四边形ABCD是正方形,
∴DG=DE,DC=DA=AB=4,∠GDE=∠ADC=90°,
∴∠ADG=∠CDE,
∴△ADG≌△CDE(SAS),
∴AG=CE,
∴AE+AG=AE+EC=ACAD=4.
(3)如图,作EH⊥DF于H.
∵四边形ABCD是正方形,
∴AB=AD=4,AB∥CD,
∵F是AB中点,
∴AF=FB
∴DF2,
∵△DEF是等腰直角三角形,EH⊥DF,
∴DH=HF,
∴EHDF,
∵AF∥CD,
∴AF:CD=FM:MD=1:2,
∴FM,
∴HM=HF﹣FM,
在Rt△EHM中,EM.
30.(1)证明:∵正方形ABCD,
∴AB=AD,∠BAD=90°,
∵AF⊥AC,
∴∠EAF=90°,
∴∠BAF=∠EAD,
在△ADE和△ABF中
∴△ADE≌△ABF(SAS),
∴BF=DE;
(2)解:当点E运动到AC的中点时四边形AFBE是正方形,
理由:∵点E运动到AC的中点,AB=BC,
∴BE⊥AC,BE=AEAC,
∵AF=AE,
∴BE=AF=AE,
又∵BE⊥AC,∠FAE=∠BEC=90°,
∴BE∥AF,
∵BE=AF,
∴得平行四边形AFBE,
∵∠FAE=90°,AF=AE,
∴四边形AFBE是正方形.
31.证明:(1)连接GE,
∵AB∥CD,
∴∠AEG=∠CGE,
∵GF∥HE,
∴∠HEG=∠FGE,
∴∠HEA=∠CGF;
(2)∵四边形ABCD是正方形,
∴∠D=∠A=90°,
∵四边形EFGH是菱形,
∴HG=HE,
在Rt△HAE和Rt△GDH中,
,
∴Rt△HAE≌Rt△GDH(HL),
∴∠AHE=∠DGH,又∠DHG+∠DGH=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∴菱形EFGH为正方形;
32.证明:(1)∵四边形ABCD是正方形,
∴∠DAB=90°,AC平分∠DAB,
∵PM⊥AD,PN⊥AB,
∴∠PMA=∠PNA=90°,
∴四边形MANP是矩形,
∵AC平分∠DAB,PM⊥AD,PN⊥AB,
∴PM=PN,
∴四边形MANP是正方形;
(2)∵四边形ABCD是正方形,
∴PM=PN,∠MPN=90°,
∵∠EPB=90°,
∴∠MPE+∠EPN=∠NPB+∠EPN=90°,
∴∠MPE=∠NPB,
在△EPM和△BPN中,
∵,
∴△EPM≌△BPN(ASA),
∴EM=BN.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
