2022—2023学年人教版数学七年级上册1.2.4绝对值 课件 (共16页)
文档属性
| 名称 | 2022—2023学年人教版数学七年级上册1.2.4绝对值 课件 (共16页) |

|
|
| 格式 | zip | ||
| 文件大小 | 729.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 17:03:37 | ||
图片预览





文档简介
(共16张PPT)
1.2.4 绝对值
想一想:3与-3有什么相同点? 与- 呢?5与-5呢?你还能举出这样的两个数吗?
如果两个数只有符号不同,那么称其中一个数为另一个数的相反数,也称这两个数互为相反数。特别地,0的相反数是0.
画出数轴、并用数轴上的点表示下列各数:
-1.5 , 0 , -6 ,2 , +6 ,-3 ,3
做一做
解:
+6
3
2
0
-1.5
-3
-6
0
1
2
3
4
-1
-2
-3
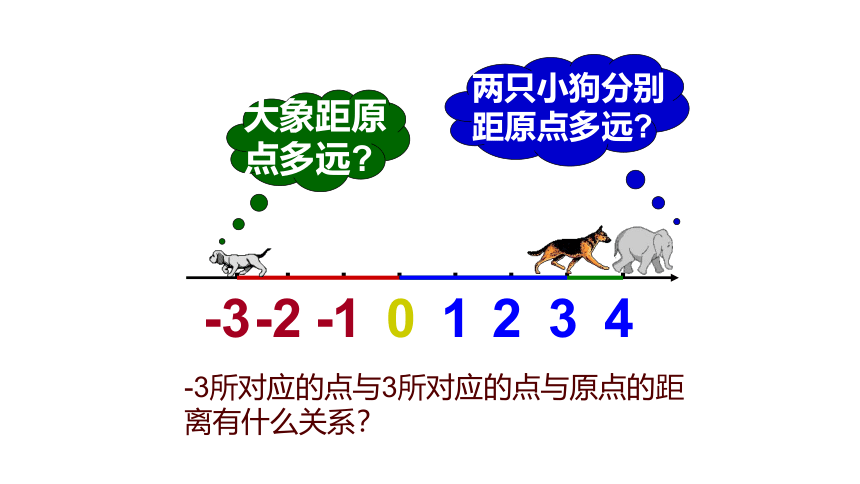
大象距原点多远
两只小狗分别距原点多远
-3所对应的点与3所对应的点与原点的距离有什么关系?
在生活中,有些问题我们只考虑数的大小而不考虑方向,如:每天早上,同学们从各自的家中走往学校所用的时间不同,决定时间的因素是你家距学校的路程,而没有强调你在学校所处的方向。再如:为了计算汽车行驶所耗的汽油,起主要作用的是汽车行驶的路程而不是行驶的方向,这就需要引进一个新的概念──绝对值。
0
6
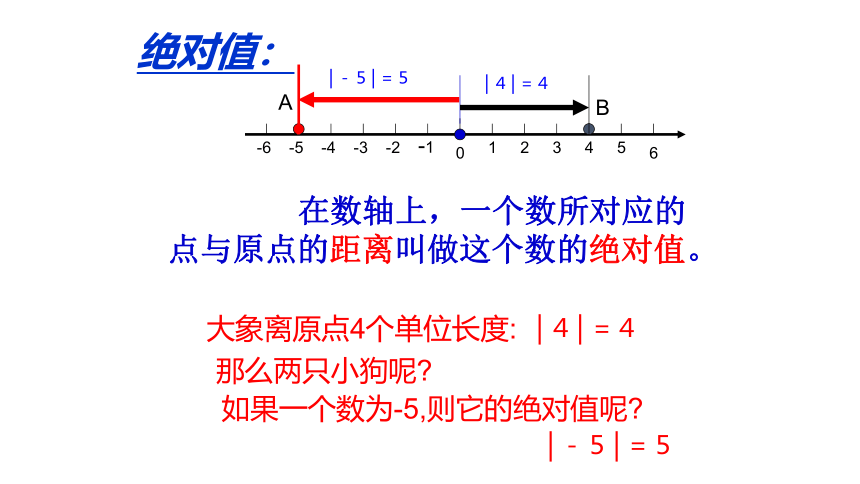
在数轴上,一个数所对应的点与原点的距离叫做这个数的绝对值。
-1
-2
-3
-4
-5
-6
1
2
3
4
5
B
A
│-5│=5
│4│=4
绝对值:
大象离原点4个单位长度:
│4│=4
那么两只小狗呢
如果一个数为-5,则它的绝对值呢
│-5│=5
拓展新知,完善新知
结论1
一个正数的绝对值是它本身;
根据合作学习,给学生充分的思考时间,通过分组讨论,得到绝对值的性质.
合作学习
结论2
一个负数的绝对值是它的相反数;
结论3
零的绝对值是零.
拓展新知,完善新知
根据合作学习,给学生充分的思考时间,通过分组讨论,得到绝对值的性质.
合作学习
性质1
一个正数的绝对值是正数;一个负数的绝对值是它的相反数;零的绝对值是零;
性质2
互为相反数的两个数的绝对值相等.
拓展新知,完善新知
如果是字母 ,那么它的绝对值又会是什么情况?再次给予学生充分讨论的时间.
(2) 绝对值等于本身的数有哪些 (正数和0)
提问
(3) 绝对值等于它相反数的数有哪些 (负数和0)
(1) 对于任意一个有理数 ,它的绝对值的正负性如何?(大于或等于0)
巩固新知,形成技能
(1)如果输出结果是2,输入的数为负数,那个输入的数是 - 2 .
(2)如果输出结果是8,那输入的数应是 8 或 - 8 .
做一做
4
-0.3
0
0.3
4
0.3
0
0.3
设计意图:培养学生利用知识的能力,让学生懂得利用绝对值的性
质求一个数的绝对值,关键是要判断这个数的正负性.
4
-0.3
0
0.3
4
0.3
0
0.3
做一做
解:根据题意可知
x-4=0,y-3=0,
所以x=4,y=3,故x+y=7.
归纳总结: 几个非负数的和为0,则这几个数都为0.
1.判断并改错:
(1)一个数的绝对值等于本身,则这个数一定是正数
( )
(2)一个数的绝对值等于它的相反数,这个数一定是
负数; ( )
(3)如果两个数的绝对值相等,那么这两个数一定
相等; ( )
(4)如果两个数不相等,那么这两个数的绝对值
一定不等; ( )
(5)有理数的绝对值一定是非负数. ( )
当堂练习
0
非负数
非正数
±2
2.____的相反数是它本身,_______的绝对值
是它本身,_______的绝对值是它的相反数.
3.|- |的相反数是 ;若| |=2,则
= _____.
4.求下列各数的绝对值:3,3.14, ,-2.8.
|3|=3;|3.14|=3.14; |-2.8|=2.8.
解:
-
5.化简:
-b
a-b
| 0.2 |=
| b |= (b<0)
| a – b | = (a>b)
0.2
1.数轴上表示数a的点与原点的距离叫做数a的绝对值.
2.绝对值的性质
(1)|a|≥0;
(2)
课堂小结
1.2.4 绝对值
想一想:3与-3有什么相同点? 与- 呢?5与-5呢?你还能举出这样的两个数吗?
如果两个数只有符号不同,那么称其中一个数为另一个数的相反数,也称这两个数互为相反数。特别地,0的相反数是0.
画出数轴、并用数轴上的点表示下列各数:
-1.5 , 0 , -6 ,2 , +6 ,-3 ,3
做一做
解:
+6
3
2
0
-1.5
-3
-6
0
1
2
3
4
-1
-2
-3
大象距原点多远
两只小狗分别距原点多远
-3所对应的点与3所对应的点与原点的距离有什么关系?
在生活中,有些问题我们只考虑数的大小而不考虑方向,如:每天早上,同学们从各自的家中走往学校所用的时间不同,决定时间的因素是你家距学校的路程,而没有强调你在学校所处的方向。再如:为了计算汽车行驶所耗的汽油,起主要作用的是汽车行驶的路程而不是行驶的方向,这就需要引进一个新的概念──绝对值。
0
6
在数轴上,一个数所对应的点与原点的距离叫做这个数的绝对值。
-1
-2
-3
-4
-5
-6
1
2
3
4
5
B
A
│-5│=5
│4│=4
绝对值:
大象离原点4个单位长度:
│4│=4
那么两只小狗呢
如果一个数为-5,则它的绝对值呢
│-5│=5
拓展新知,完善新知
结论1
一个正数的绝对值是它本身;
根据合作学习,给学生充分的思考时间,通过分组讨论,得到绝对值的性质.
合作学习
结论2
一个负数的绝对值是它的相反数;
结论3
零的绝对值是零.
拓展新知,完善新知
根据合作学习,给学生充分的思考时间,通过分组讨论,得到绝对值的性质.
合作学习
性质1
一个正数的绝对值是正数;一个负数的绝对值是它的相反数;零的绝对值是零;
性质2
互为相反数的两个数的绝对值相等.
拓展新知,完善新知
如果是字母 ,那么它的绝对值又会是什么情况?再次给予学生充分讨论的时间.
(2) 绝对值等于本身的数有哪些 (正数和0)
提问
(3) 绝对值等于它相反数的数有哪些 (负数和0)
(1) 对于任意一个有理数 ,它的绝对值的正负性如何?(大于或等于0)
巩固新知,形成技能
(1)如果输出结果是2,输入的数为负数,那个输入的数是 - 2 .
(2)如果输出结果是8,那输入的数应是 8 或 - 8 .
做一做
4
-0.3
0
0.3
4
0.3
0
0.3
设计意图:培养学生利用知识的能力,让学生懂得利用绝对值的性
质求一个数的绝对值,关键是要判断这个数的正负性.
4
-0.3
0
0.3
4
0.3
0
0.3
做一做
解:根据题意可知
x-4=0,y-3=0,
所以x=4,y=3,故x+y=7.
归纳总结: 几个非负数的和为0,则这几个数都为0.
1.判断并改错:
(1)一个数的绝对值等于本身,则这个数一定是正数
( )
(2)一个数的绝对值等于它的相反数,这个数一定是
负数; ( )
(3)如果两个数的绝对值相等,那么这两个数一定
相等; ( )
(4)如果两个数不相等,那么这两个数的绝对值
一定不等; ( )
(5)有理数的绝对值一定是非负数. ( )
当堂练习
0
非负数
非正数
±2
2.____的相反数是它本身,_______的绝对值
是它本身,_______的绝对值是它的相反数.
3.|- |的相反数是 ;若| |=2,则
= _____.
4.求下列各数的绝对值:3,3.14, ,-2.8.
|3|=3;|3.14|=3.14; |-2.8|=2.8.
解:
-
5.化简:
-b
a-b
| 0.2 |=
| b |= (b<0)
| a – b | = (a>b)
0.2
1.数轴上表示数a的点与原点的距离叫做数a的绝对值.
2.绝对值的性质
(1)|a|≥0;
(2)
课堂小结
