青岛版九年级上册2.5.1 解直角三角形的应用课件(共15张PPT)
文档属性
| 名称 | 青岛版九年级上册2.5.1 解直角三角形的应用课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 435.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 19:56:20 | ||
图片预览





文档简介
(共15张PPT)
2.5 解直角三角形的应用
tanA=
b
a
∠A + ∠B = 90 °;
勾股定理:a2+b2=c2 ;
(3)角与边之间的关系:
(2)边之间的关系:
(1)角之间的关系:
sinA=
c
a
,
cosA=
c
b
,
2. 什么叫解直角三角形?如果知道直角三角形的几个元素就可以求其他的元素?有几种情况?
两个元素(至少一个是边)
两条边或一边一角
1.直角三角形的边角关系:
知识回顾:
tanA=
b
a
∠A + ∠B = 90 °;
勾股定理:a2+b2=c2 ;
(3)角与边之间的关系:
(2)边之间的关系:
(1)角之间的关系:
sinA=
c
a
,
cosA=
c
b
,
2. 如果知道直角三角形的几个元素就可以求其
他的元素?有几种情况?
两个元素(至少一个是边)
两条边或一边一角
1.直角三角形的边角关系:
温故知新
新课引入
在日常生活中,我们经常会碰到一些与直角三角形有关的实际问题.对于这些问题,我们可以用所学的解直角三角形的知识来加以解决.
40.95保留一位小数时注意为41.0
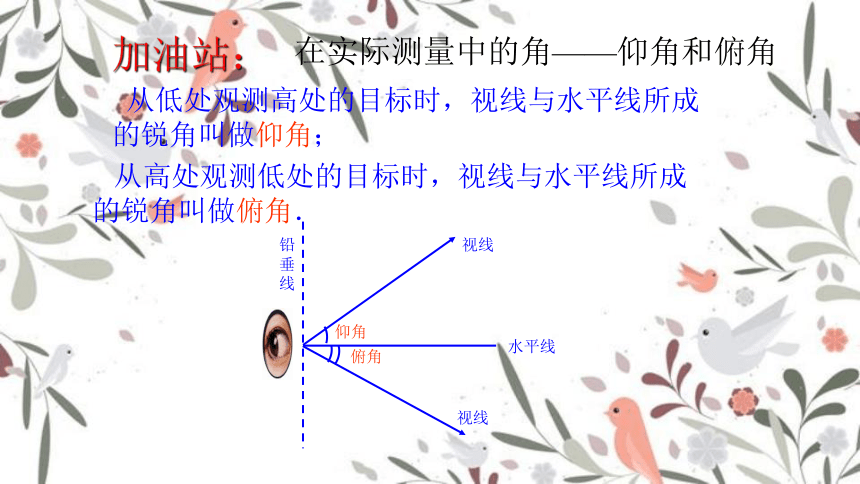
加油站:
铅垂线
水平线
仰角
俯角
在实际测量中的角——仰角和俯角
视线
视线
从高处观测低处的目标时,视线与水平线所成
的锐角叫做俯角.
从低处观测高处的目标时,视线与水平线所成
的锐角叫做仰角;
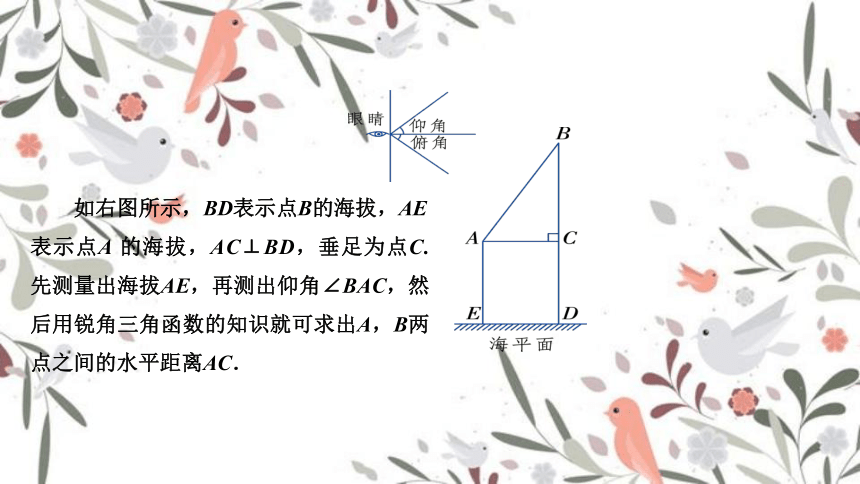
如右图所示,BD表示点B的海拔,AE 表示点A 的海拔,AC⊥BD,垂足为点C. 先测量出海拔AE,再测出仰角∠BAC,然后用锐角三角函数的知识就可求出A,B两点之间的水平距离AC.
15 东营)4月26日,2015黄河口国际马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是 米。
1
2
∠1= 30° ∠2 = 45° CD=200,求AB的长。
200
200
AB=
如上图所示,从山坡脚下点 A 上坡走到点B时,升高的高度h(即线段BC的长度)与水平前进的距离l(即线段AC 的长度)的比叫作坡度,用字母i表示,即
(坡度通常写成1:m 的形式).
坡度越大,山坡越陡.
在上图中,∠BAC 叫作坡角(即山坡与地平面的
夹角),记作 ,显然,坡度等于坡角的正切,即
同侧型
1、已知AC⊥BC,∠B=30°,∠D=45°,AC=1。求图中其它线段的长?
2、已知AC⊥BC,∠B=30°,∠D=45°,BD= -1。求图中其它线段的长?
思考:其它条件不变,将AC的长换成AB、AD、BC、CD可以吗?
【知识迁移】
(16十堰)在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为 米.(结果保留根号)
EF∥MN,AB=30,CD=10.∠1=45 °, ∠2=30 °,求宽。
1
2
D
练习1 .如图,在电线杆上离地面6 米处用拉线固定电线杆,拉线和地面之间的夹角为60° , 求拉线AC 的长和拉线下端点A 与线杆底部D 的距离(精确到0 . 1 米).
2.如图,一架梯子斜靠在墙上,梯子顶端到地面的距离BC = 3.2 米,底端到墙根的距离
AC = 2.4 米.
(1)求梯子的长度和梯子与地面所成角的大小(精确到1 ' ) ;
(2) 如果把梯子的底端到墙角的距离减少0 . 4 米,那么梯子与地面所成的角是多少?
6米
A
B
C
D
A
C
B
AC≈5.2米
AD=3.0米
∠BAC≈53°8′
AB=4.0米,
∠BAC=60°
例、如图,平地上一棵树高为5米,两次观察地面上的影子,第一次是阳光与地面成45°时,第二次是阳光与地面成30°时,求第二次观察到的影子比第一次长多少米?
30°
45°
A
B
C
D
30°
45°
A
B
C
D
课堂小结
通过这节课的学习,相信同学们一定学到了不少的新的知识了吧,课下一定要积极的落实,对新学的知识进行复习巩固,对新知识预习
2.5 解直角三角形的应用
tanA=
b
a
∠A + ∠B = 90 °;
勾股定理:a2+b2=c2 ;
(3)角与边之间的关系:
(2)边之间的关系:
(1)角之间的关系:
sinA=
c
a
,
cosA=
c
b
,
2. 什么叫解直角三角形?如果知道直角三角形的几个元素就可以求其他的元素?有几种情况?
两个元素(至少一个是边)
两条边或一边一角
1.直角三角形的边角关系:
知识回顾:
tanA=
b
a
∠A + ∠B = 90 °;
勾股定理:a2+b2=c2 ;
(3)角与边之间的关系:
(2)边之间的关系:
(1)角之间的关系:
sinA=
c
a
,
cosA=
c
b
,
2. 如果知道直角三角形的几个元素就可以求其
他的元素?有几种情况?
两个元素(至少一个是边)
两条边或一边一角
1.直角三角形的边角关系:
温故知新
新课引入
在日常生活中,我们经常会碰到一些与直角三角形有关的实际问题.对于这些问题,我们可以用所学的解直角三角形的知识来加以解决.
40.95保留一位小数时注意为41.0
加油站:
铅垂线
水平线
仰角
俯角
在实际测量中的角——仰角和俯角
视线
视线
从高处观测低处的目标时,视线与水平线所成
的锐角叫做俯角.
从低处观测高处的目标时,视线与水平线所成
的锐角叫做仰角;
如右图所示,BD表示点B的海拔,AE 表示点A 的海拔,AC⊥BD,垂足为点C. 先测量出海拔AE,再测出仰角∠BAC,然后用锐角三角函数的知识就可求出A,B两点之间的水平距离AC.
15 东营)4月26日,2015黄河口国际马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是 米。
1
2
∠1= 30° ∠2 = 45° CD=200,求AB的长。
200
200
AB=
如上图所示,从山坡脚下点 A 上坡走到点B时,升高的高度h(即线段BC的长度)与水平前进的距离l(即线段AC 的长度)的比叫作坡度,用字母i表示,即
(坡度通常写成1:m 的形式).
坡度越大,山坡越陡.
在上图中,∠BAC 叫作坡角(即山坡与地平面的
夹角),记作 ,显然,坡度等于坡角的正切,即
同侧型
1、已知AC⊥BC,∠B=30°,∠D=45°,AC=1。求图中其它线段的长?
2、已知AC⊥BC,∠B=30°,∠D=45°,BD= -1。求图中其它线段的长?
思考:其它条件不变,将AC的长换成AB、AD、BC、CD可以吗?
【知识迁移】
(16十堰)在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为 米.(结果保留根号)
EF∥MN,AB=30,CD=10.∠1=45 °, ∠2=30 °,求宽。
1
2
D
练习1 .如图,在电线杆上离地面6 米处用拉线固定电线杆,拉线和地面之间的夹角为60° , 求拉线AC 的长和拉线下端点A 与线杆底部D 的距离(精确到0 . 1 米).
2.如图,一架梯子斜靠在墙上,梯子顶端到地面的距离BC = 3.2 米,底端到墙根的距离
AC = 2.4 米.
(1)求梯子的长度和梯子与地面所成角的大小(精确到1 ' ) ;
(2) 如果把梯子的底端到墙角的距离减少0 . 4 米,那么梯子与地面所成的角是多少?
6米
A
B
C
D
A
C
B
AC≈5.2米
AD=3.0米
∠BAC≈53°8′
AB=4.0米,
∠BAC=60°
例、如图,平地上一棵树高为5米,两次观察地面上的影子,第一次是阳光与地面成45°时,第二次是阳光与地面成30°时,求第二次观察到的影子比第一次长多少米?
30°
45°
A
B
C
D
30°
45°
A
B
C
D
课堂小结
通过这节课的学习,相信同学们一定学到了不少的新的知识了吧,课下一定要积极的落实,对新学的知识进行复习巩固,对新知识预习
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
