2022-2023学年京改版九年级数学上册19.4二次函数的应用 课件(共15张PPT)
文档属性
| 名称 | 2022-2023学年京改版九年级数学上册19.4二次函数的应用 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 16:59:14 | ||
图片预览





文档简介
(共15张PPT)
19.4二次函数的应用
教学目标
1.分析实际问题中变量之间的二次函数关系.
2.会运用二次函数求实际问题中的最大值或最小值.
3.能应用二次函数的性质解决图形中最大面积问题.
如何运用二次函数求实际问题中的最大值或最小值
复习思考
首先应当求出函数解析式和自变量的取值范围,然后通过配方变形,或利用公式求它的最大值或最小值。
注意:有此求得的最大值或最小值对应的字变量的值必须在自变量的取值范围内 。
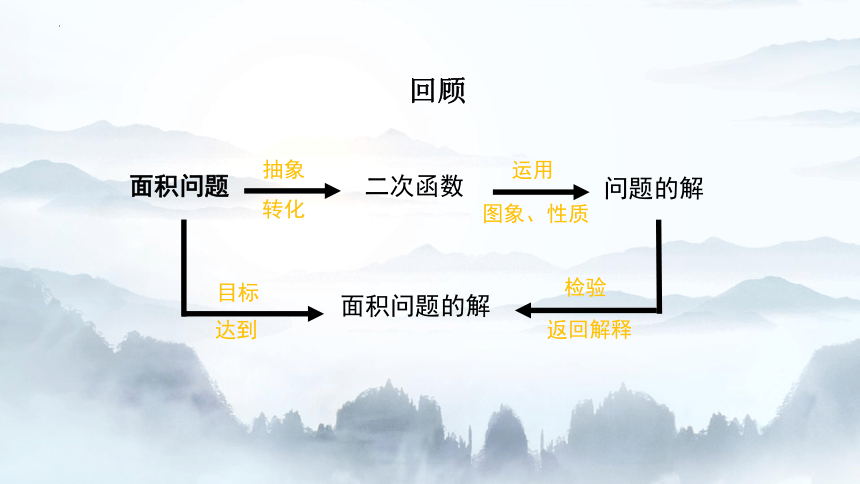
回顾
面积问题
抽象
转化
二次函数
运用
图象、性质
问题的解
返回解释
检验
面积问题的解
达到
目标
复习引入
写出下列抛物线的开口方向、对称轴和顶点坐标.
(1)y=x2-4x-5; (2)y=-x2-3x+4.
解:(1)开口方向:向上;对称轴:x=2;
顶点坐标:(2,-9);
(2)开口方向:向下;对称轴:x= ;
顶点坐标:( , );
由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,
当 时,
二次函数 y = ax 2 + bx + c 有最小(大) 值
想一想:如何求出二次函数 y = ax 2 + bx + c 的最小(大)值?
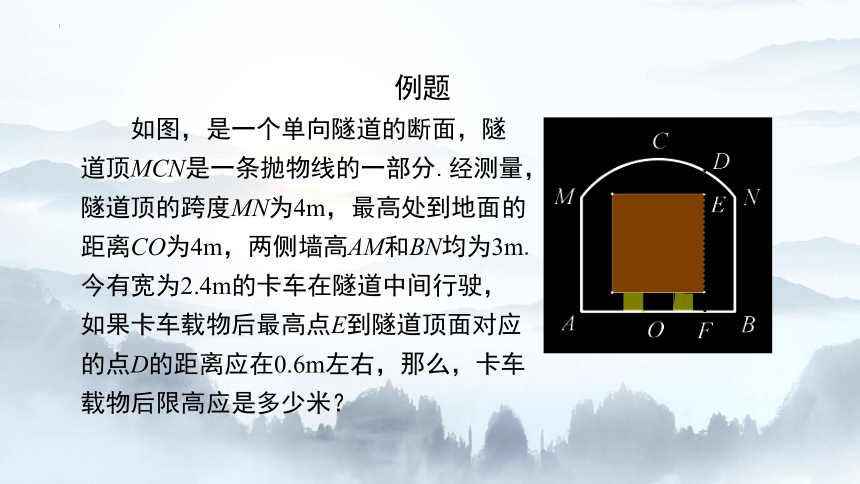
例题
如图,是一个单向隧道的断面,隧道顶MCN是一条抛物线的一部分.经测量,隧道顶的跨度MN为4m,最高处到地面的距离CO为4m,两侧墙高AM和BN均为3m.今有宽为2.4m的卡车在隧道中间行驶,如果卡车载物后最高点E到隧道顶面对应的点D的距离应在0.6m左右,那么,卡车载物后限高应是多少米?
4
1.2
2
2
0.6
4
4
3
3
分析
隧道顶MCN是一条抛物线的一部分;
隧道顶的跨度MN为4m;
最高处到地面的距离CO为4m;
两侧墙高AM和BN均为3m;
今有宽为2.4m的卡车在隧道中间行驶;
卡车载物后最高点E到隧道顶面对应
的点D的距离应在0.6m左右;
求卡车载物后限高应是多少米?
已知:如图,点C为抛物线MCN的顶点,OC=4 , MN=AB=4 ,AM=BN=3 ,OA=OB=2,OF=1.2,DE=0.6,求EF的长?
EF = DF - DE
0.6
4
4
3
4
2
2
分析
3
0.6
1.2
例题
小丽家门前有一块空地,为了美化生活环境,小丽的爸爸准备修建一个矩形花圃,他买回了24米长的不锈钢管准备作为花圃的围栏(如图)问:花圃的一边AD为多少米时,花圃的面积最大?最大值是多少?
矩形ABCD的周长是24米
?
分析
矩形ABCD的周长是24米
?
5
7
35
6
6
36
8
4
32
9
3
27
一起做一做
悬索桥两端主塔塔顶之间的主悬钢索,其形状可近似地看作抛物线,水平桥面与主悬钢索之间用垂直钢索连接.已知两端主塔之间的水平距离为900 m,两主塔塔顶距桥面的高度为81.5 m,主悬钢索最低点离桥面的高度为0.5 m.
(1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图所示,求这条抛物线对应的函数表达式;
y
x
O
-450
450
解:根据题意,得抛物线的顶点坐标为(0,0.5),
对称轴为y轴,设抛物线的函数表达式为y=ax2+0.5.
抛物线经过点(450,81.5),代入上式,得
81.5=a 4502+0.5.
解得
故所求表达式为
(1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图所示,求这条抛物线对应的函数表达式;
y
x
O
-450
450
(2)计算距离桥两端主塔分别为100m,50m处垂直钢索的长.
y
x
O
-450
450
解:当x=450-100=350(m)时,得
当x=450-50=400(m)时,得
几何面积最值问题
一个关键
一个注意
建立函数关系式
常见几何图形的面积公式
依 据
最值有时不在顶点处,则要利用函数的增减性来确定
(二次函数的图象和性质)
实际问题
数学模型
转化
回归
(实物中的抛物线形问题)
课堂小结
19.4二次函数的应用
教学目标
1.分析实际问题中变量之间的二次函数关系.
2.会运用二次函数求实际问题中的最大值或最小值.
3.能应用二次函数的性质解决图形中最大面积问题.
如何运用二次函数求实际问题中的最大值或最小值
复习思考
首先应当求出函数解析式和自变量的取值范围,然后通过配方变形,或利用公式求它的最大值或最小值。
注意:有此求得的最大值或最小值对应的字变量的值必须在自变量的取值范围内 。
回顾
面积问题
抽象
转化
二次函数
运用
图象、性质
问题的解
返回解释
检验
面积问题的解
达到
目标
复习引入
写出下列抛物线的开口方向、对称轴和顶点坐标.
(1)y=x2-4x-5; (2)y=-x2-3x+4.
解:(1)开口方向:向上;对称轴:x=2;
顶点坐标:(2,-9);
(2)开口方向:向下;对称轴:x= ;
顶点坐标:( , );
由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,
当 时,
二次函数 y = ax 2 + bx + c 有最小(大) 值
想一想:如何求出二次函数 y = ax 2 + bx + c 的最小(大)值?
例题
如图,是一个单向隧道的断面,隧道顶MCN是一条抛物线的一部分.经测量,隧道顶的跨度MN为4m,最高处到地面的距离CO为4m,两侧墙高AM和BN均为3m.今有宽为2.4m的卡车在隧道中间行驶,如果卡车载物后最高点E到隧道顶面对应的点D的距离应在0.6m左右,那么,卡车载物后限高应是多少米?
4
1.2
2
2
0.6
4
4
3
3
分析
隧道顶MCN是一条抛物线的一部分;
隧道顶的跨度MN为4m;
最高处到地面的距离CO为4m;
两侧墙高AM和BN均为3m;
今有宽为2.4m的卡车在隧道中间行驶;
卡车载物后最高点E到隧道顶面对应
的点D的距离应在0.6m左右;
求卡车载物后限高应是多少米?
已知:如图,点C为抛物线MCN的顶点,OC=4 , MN=AB=4 ,AM=BN=3 ,OA=OB=2,OF=1.2,DE=0.6,求EF的长?
EF = DF - DE
0.6
4
4
3
4
2
2
分析
3
0.6
1.2
例题
小丽家门前有一块空地,为了美化生活环境,小丽的爸爸准备修建一个矩形花圃,他买回了24米长的不锈钢管准备作为花圃的围栏(如图)问:花圃的一边AD为多少米时,花圃的面积最大?最大值是多少?
矩形ABCD的周长是24米
?
分析
矩形ABCD的周长是24米
?
5
7
35
6
6
36
8
4
32
9
3
27
一起做一做
悬索桥两端主塔塔顶之间的主悬钢索,其形状可近似地看作抛物线,水平桥面与主悬钢索之间用垂直钢索连接.已知两端主塔之间的水平距离为900 m,两主塔塔顶距桥面的高度为81.5 m,主悬钢索最低点离桥面的高度为0.5 m.
(1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图所示,求这条抛物线对应的函数表达式;
y
x
O
-450
450
解:根据题意,得抛物线的顶点坐标为(0,0.5),
对称轴为y轴,设抛物线的函数表达式为y=ax2+0.5.
抛物线经过点(450,81.5),代入上式,得
81.5=a 4502+0.5.
解得
故所求表达式为
(1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图所示,求这条抛物线对应的函数表达式;
y
x
O
-450
450
(2)计算距离桥两端主塔分别为100m,50m处垂直钢索的长.
y
x
O
-450
450
解:当x=450-100=350(m)时,得
当x=450-50=400(m)时,得
几何面积最值问题
一个关键
一个注意
建立函数关系式
常见几何图形的面积公式
依 据
最值有时不在顶点处,则要利用函数的增减性来确定
(二次函数的图象和性质)
实际问题
数学模型
转化
回归
(实物中的抛物线形问题)
课堂小结
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
