人教A版(2019)高中数学必修第一册 5.1任意角和弧度制 课件(共34张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第一册 5.1任意角和弧度制 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 936.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 10:37:38 | ||
图片预览









文档简介
(共34张PPT)
5.1 任意角和弧度制
第五章 三角函数
目录
二、知识讲解
三、小结
四、练习
一、上节回溯
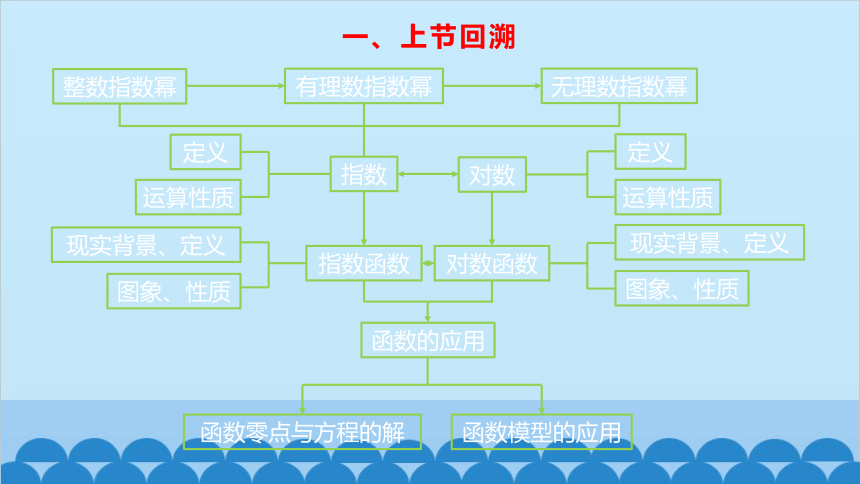
一、上节回溯
函数的应用
指数函数
对数函数
有理数指数幂
定义
运算性质
整数指数幂
无理数指数幂
指数
对数
定义
运算性质
现实背景、定义
图象、性质
现实背景、定义
图象、性质
函数零点与方程的解
函数模型的应用
二、知识讲解
圆周运动是一种常见的周期性变化现象.如图 5.1-1,⊙O 上的点 P 以 A 为起点做逆时针方向的旋转.如何刻画点 P 的位置变化呢?
P
O
A
α
图 5.1-1
二、知识讲解
5.1.1 任意角
现实生活中随处可见超出 0°~360° 范围的角.例如,体操中有“前空翻转体 540 度”“后空翻转体 720 度”这样的动作名称,这里不仅有超出 0°~360° 范围的角,而且旋转的方向也不相同;又如,图 5.1-2 是两个齿轮旋转的示意图,被动轮随着主动轮的旋转而旋转,而且被动轮与主动轮有相反的旋转方向.这样,OA 绕点 O 旋转所成的角与 O′B 绕点 O′ 旋转所成的角就会有不同的方向.因此,要准确地描述这些现象,不仅要知道旋转的度数,还要知道旋转的方向,这就需要对角的概念进行推广.
被动轮
主动轮
图 5.1-2
二、知识讲解
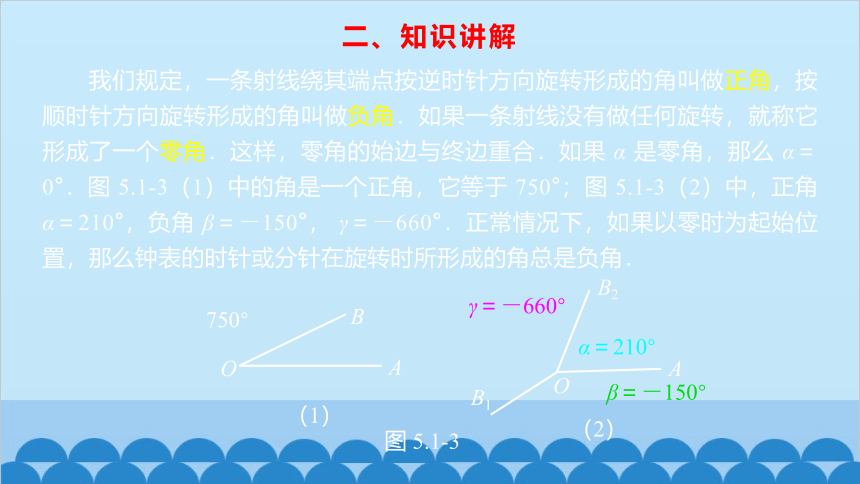
我们规定,一条射线绕其端点按逆时针方向旋转形成的角叫做正角,按顺时针方向旋转形成的角叫做负角.如果一条射线没有做任何旋转,就称它形成了一个零角.这样,零角的始边与终边重合.如果 α 是零角,那么 α=0°.图 5.1-3(1)中的角是一个正角,它等于 750°;图 5.1-3(2)中,正角α=210°,负角 β=-150°, γ=-660°.正常情况下,如果以零时为起始位置,那么钟表的时针或分针在旋转时所形成的角总是负角.
B
O
A
750°
(1)
图 5.1-3
B2
O
A
α=210°
(2)
β=-150°
γ=-660°
B1
二、知识讲解
这样,我们就把角的概念推广到了任意角(any angle),包括正角、负角和零角.设角 α 由射线 OA 绕端点 O 旋转而成,角 β 由射线 O′A′ 绕端点O′ 旋转而成.如果它们的旋转方向相同且旋转量相等,那么就称 α=β.
设 α,β 是任意两个角.我们规定,把角 α 的终边旋转角 β,这时终边所对应的角是 α+β.
二、知识讲解
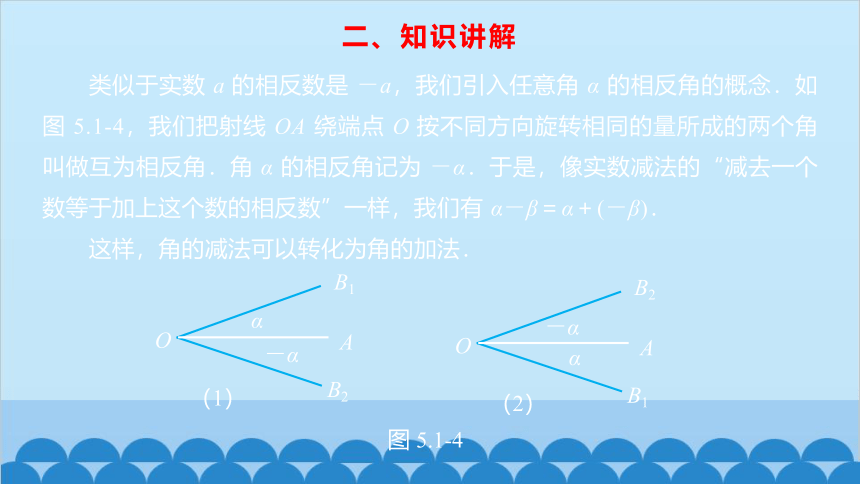
类似于实数 a 的相反数是 -a,我们引入任意角 α 的相反角的概念.如图 5.1-4,我们把射线 OA 绕端点 O 按不同方向旋转相同的量所成的两个角叫做互为相反角.角 α 的相反角记为 -α.于是,像实数减法的“减去一个数等于加上这个数的相反数”一样,我们有 α-β=α+(-β).
这样,角的减法可以转化为角的加法.
B2
O
A
-α
(1)
α
B1
B1
O
A
-α
(2)
α
B2
图 5.1-4
二、知识讲解
我们通常在直角坐标系内讨论角.为了方便,使角的顶点与原点重合,角的始边与 x 轴的非负半轴重合.那么,角的终边在第几象限,就说这个角是第几象限角.例如,图 5.1-5 中的 30° 角、-120°角分别是第一象限角和第三象限角.如果角的终边在坐标轴上,那么就认为这个角不属于任何一个象限.
x
y
O
30°
-120°
图 5.1-5
你能说说在直角坐标系内讨论角的好处吗?
?
二、知识讲解
将角按照上述方法放在直角坐标系中后,给定一个角,就有唯一的一条终边与之对应.反之,对于直角坐标系内任意一条射线 OB(图 5.1-6),以它为终边的角是否唯一?如果不唯一,那么终边相同的角有什么关系?
探究
x
y
O
-32°
-392°
图 5.1-6
B
328°
二、知识讲解
328°=-32°+360°(这里 k=___),-392°=-32°-360°(这里 k=___).
设 S={β | β=-32°+k · 360°,k∈Z}, 则 328°,-392° 角都是 S 的元素,-32° 角也是 S 的元素(此时 k=___).因此,所有与 -32° 角终边相同的角,连同 -32° 角在内,都是集合 S 的元素;反过来,集合 S 的任一元素显然与-32° 角的终边相同.
一般地,我们有:
所有与角 α 终边相同的角,连同角 α 在内,可构成一个集合
S={β | β=α +k · 360°,k∈Z},
即任一与角 α 终边相同的角,都可以表示成角 α 与整数个周角的和.
二、知识讲解
例1 在 0°~360° 范围内,找出与 -950°12′ 角终边相同的角,并判定它是第几象限角.
解:-950°12′=129°48′-3×360°,所以在 0°~360° 范围内,与 -950°12′ 角终边相同的角是 129°48′,它是第二象限角.
二、知识讲解
例2 写出终边在 y 轴上的角的集合.
解:在 0°~360° 范围内,终边在 y 轴上的角有两个,即 90°,270° 角(图 5.1-7).因此,所有与 90° 角终边相同的角构成集合
S1={β | β=90°+k · 360°,k∈Z},
而所有与 270° 角终边相同的角构成集合
S2={β | β=270°+k · 360°,k∈Z},
于是,终边在 y 轴上的角的集合
S=S1∪S2={β | β=90°+2k · 180°,k∈Z}∪{β | β=90°+180°+2k · 180°,k∈Z}
={β | β=90°+2k · 180°,k∈Z}∪{β | β=90°+(2k+1)180°,k∈Z}
={β | β=90°+n · 180°,n∈Z}.
x
y
O
90°
图 5.1-7
270°
二、知识讲解
例3 写出终边在直线 y=x 上的角的集合 S.S 中满足不等式 -360°≤β<720° 的元素 β 有哪些?
解:如图 5.1-8,在直角坐标系中画出直线 y=x,可以发现它与 x 轴的夹角是 45°,在 0°~360° 范围内,终边在直线 y=x 上的角有两个:45°,225°.因此,终边在直线 y=x 上的角的集合
S={β | β=45°+k · 360°,k∈Z}∪
{β | β=225°+k · 360°,k∈Z}
={β | β=45°+n · 180°,n∈Z}.
x
y
O
45°
图 5.1-8
225°
y=x
二、知识讲解
S 中适合不等式-360°≤β<720° 的元素 β 有
45°-2×180°=-315°,
45°-1×180°=-135°,
45°+0×180°=45°,
45°+1×180°=225°,
45°+2×180°=405°,
45°+3×180°=585°.
二、知识讲解
5.1.2 弧度制
二、知识讲解
A
B
O
α
图 5.1-9
P
P1
二、知识讲解
探究
可以发现,圆心角 α 所对的弧长与半径的比值,只与 α 的大小有关.也就是说,这个比值随 α 的确定而唯一确定.这就启发我们,可以利用圆的弧长与半径的关系度量圆心角.
A
B
O
α
图 5.1-10
P
P1
Q
Q1
二、知识讲解
A
B
O
1 rad
图 5.1-11
1
二、知识讲解
角度制、弧度制都是角的度量制,它们之间应该可以换算.如何换算呢?
探究
其中,α 的正负由角 α 的终边的旋转方向决定,即逆时针旋转为正,顺时针旋转为负.当角的终边旋转一周后继续旋转,就可以得到弧度数大于 2π 或小于 -2π 的角.这样就可以得到弧度为任意大小的角.
一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是 0.
二、知识讲解
二、知识讲解
一般地,只需根据
180°=π rad
就可以进行弧度与角度的换算了.
二、知识讲解
1.178 097 245.
因此,67°30′≈1.178 rad.
二、知识讲解
例5 将 3.14 rad 换算成角度(用度数表示,精确到 0.001).
解:利用计算器有
179.908 747 7.
因此,3.14 rad≈179.909°.
二、知识讲解
360°
150°
135°
度
弧度
45°
30°
120°
π
0°
二、知识讲解
角的概念推广后,在弧度制下,角的集合与实数集 R 之间建立起一一对应的关系:每一个角都有唯一的一个实数(等于这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应(图 5.1-12).
图 5.1-12
正角
零角
正实数
负角
负实数
0
二、知识讲解
二、知识讲解
三、小结
弧度制
正角负角零角
象限角
任意角
角的集合与实数集一一对应
终边相同的角:β=α+k · 360°,k∈Z
弧度的概念
弧度公式
弧度与角度的换算
180°=π rad
1.在 0°~360° 范围内,找出与下列各角终边相同的角,并指出它们是第几象限角:
(1)-54°18′;(2)395°8′;(3)-1 190°30′.
答案:(1)305°42′,第四象限角.(2)35°8′,第一象限角.(3)249°30′,第三象限角.
四、练习
2.写出与下列各角终边相同的角的集合,并找出集合中适合不等式 -720°≤β<360° 的元素 β:
(1)1 303°18′;(2)-225°.
答案:(1){β | β=1 303°18′+k · 360°,k∈Z},-496°42′,-136°42′,223°18′.(2){β | β=-225°+k · 360°,k∈Z},-585°,-225°,135°.
四、练习
四、练习
四、练习
谢谢观看
5.1 任意角和弧度制
第五章 三角函数
目录
二、知识讲解
三、小结
四、练习
一、上节回溯
一、上节回溯
函数的应用
指数函数
对数函数
有理数指数幂
定义
运算性质
整数指数幂
无理数指数幂
指数
对数
定义
运算性质
现实背景、定义
图象、性质
现实背景、定义
图象、性质
函数零点与方程的解
函数模型的应用
二、知识讲解
圆周运动是一种常见的周期性变化现象.如图 5.1-1,⊙O 上的点 P 以 A 为起点做逆时针方向的旋转.如何刻画点 P 的位置变化呢?
P
O
A
α
图 5.1-1
二、知识讲解
5.1.1 任意角
现实生活中随处可见超出 0°~360° 范围的角.例如,体操中有“前空翻转体 540 度”“后空翻转体 720 度”这样的动作名称,这里不仅有超出 0°~360° 范围的角,而且旋转的方向也不相同;又如,图 5.1-2 是两个齿轮旋转的示意图,被动轮随着主动轮的旋转而旋转,而且被动轮与主动轮有相反的旋转方向.这样,OA 绕点 O 旋转所成的角与 O′B 绕点 O′ 旋转所成的角就会有不同的方向.因此,要准确地描述这些现象,不仅要知道旋转的度数,还要知道旋转的方向,这就需要对角的概念进行推广.
被动轮
主动轮
图 5.1-2
二、知识讲解
我们规定,一条射线绕其端点按逆时针方向旋转形成的角叫做正角,按顺时针方向旋转形成的角叫做负角.如果一条射线没有做任何旋转,就称它形成了一个零角.这样,零角的始边与终边重合.如果 α 是零角,那么 α=0°.图 5.1-3(1)中的角是一个正角,它等于 750°;图 5.1-3(2)中,正角α=210°,负角 β=-150°, γ=-660°.正常情况下,如果以零时为起始位置,那么钟表的时针或分针在旋转时所形成的角总是负角.
B
O
A
750°
(1)
图 5.1-3
B2
O
A
α=210°
(2)
β=-150°
γ=-660°
B1
二、知识讲解
这样,我们就把角的概念推广到了任意角(any angle),包括正角、负角和零角.设角 α 由射线 OA 绕端点 O 旋转而成,角 β 由射线 O′A′ 绕端点O′ 旋转而成.如果它们的旋转方向相同且旋转量相等,那么就称 α=β.
设 α,β 是任意两个角.我们规定,把角 α 的终边旋转角 β,这时终边所对应的角是 α+β.
二、知识讲解
类似于实数 a 的相反数是 -a,我们引入任意角 α 的相反角的概念.如图 5.1-4,我们把射线 OA 绕端点 O 按不同方向旋转相同的量所成的两个角叫做互为相反角.角 α 的相反角记为 -α.于是,像实数减法的“减去一个数等于加上这个数的相反数”一样,我们有 α-β=α+(-β).
这样,角的减法可以转化为角的加法.
B2
O
A
-α
(1)
α
B1
B1
O
A
-α
(2)
α
B2
图 5.1-4
二、知识讲解
我们通常在直角坐标系内讨论角.为了方便,使角的顶点与原点重合,角的始边与 x 轴的非负半轴重合.那么,角的终边在第几象限,就说这个角是第几象限角.例如,图 5.1-5 中的 30° 角、-120°角分别是第一象限角和第三象限角.如果角的终边在坐标轴上,那么就认为这个角不属于任何一个象限.
x
y
O
30°
-120°
图 5.1-5
你能说说在直角坐标系内讨论角的好处吗?
?
二、知识讲解
将角按照上述方法放在直角坐标系中后,给定一个角,就有唯一的一条终边与之对应.反之,对于直角坐标系内任意一条射线 OB(图 5.1-6),以它为终边的角是否唯一?如果不唯一,那么终边相同的角有什么关系?
探究
x
y
O
-32°
-392°
图 5.1-6
B
328°
二、知识讲解
328°=-32°+360°(这里 k=___),-392°=-32°-360°(这里 k=___).
设 S={β | β=-32°+k · 360°,k∈Z}, 则 328°,-392° 角都是 S 的元素,-32° 角也是 S 的元素(此时 k=___).因此,所有与 -32° 角终边相同的角,连同 -32° 角在内,都是集合 S 的元素;反过来,集合 S 的任一元素显然与-32° 角的终边相同.
一般地,我们有:
所有与角 α 终边相同的角,连同角 α 在内,可构成一个集合
S={β | β=α +k · 360°,k∈Z},
即任一与角 α 终边相同的角,都可以表示成角 α 与整数个周角的和.
二、知识讲解
例1 在 0°~360° 范围内,找出与 -950°12′ 角终边相同的角,并判定它是第几象限角.
解:-950°12′=129°48′-3×360°,所以在 0°~360° 范围内,与 -950°12′ 角终边相同的角是 129°48′,它是第二象限角.
二、知识讲解
例2 写出终边在 y 轴上的角的集合.
解:在 0°~360° 范围内,终边在 y 轴上的角有两个,即 90°,270° 角(图 5.1-7).因此,所有与 90° 角终边相同的角构成集合
S1={β | β=90°+k · 360°,k∈Z},
而所有与 270° 角终边相同的角构成集合
S2={β | β=270°+k · 360°,k∈Z},
于是,终边在 y 轴上的角的集合
S=S1∪S2={β | β=90°+2k · 180°,k∈Z}∪{β | β=90°+180°+2k · 180°,k∈Z}
={β | β=90°+2k · 180°,k∈Z}∪{β | β=90°+(2k+1)180°,k∈Z}
={β | β=90°+n · 180°,n∈Z}.
x
y
O
90°
图 5.1-7
270°
二、知识讲解
例3 写出终边在直线 y=x 上的角的集合 S.S 中满足不等式 -360°≤β<720° 的元素 β 有哪些?
解:如图 5.1-8,在直角坐标系中画出直线 y=x,可以发现它与 x 轴的夹角是 45°,在 0°~360° 范围内,终边在直线 y=x 上的角有两个:45°,225°.因此,终边在直线 y=x 上的角的集合
S={β | β=45°+k · 360°,k∈Z}∪
{β | β=225°+k · 360°,k∈Z}
={β | β=45°+n · 180°,n∈Z}.
x
y
O
45°
图 5.1-8
225°
y=x
二、知识讲解
S 中适合不等式-360°≤β<720° 的元素 β 有
45°-2×180°=-315°,
45°-1×180°=-135°,
45°+0×180°=45°,
45°+1×180°=225°,
45°+2×180°=405°,
45°+3×180°=585°.
二、知识讲解
5.1.2 弧度制
二、知识讲解
A
B
O
α
图 5.1-9
P
P1
二、知识讲解
探究
可以发现,圆心角 α 所对的弧长与半径的比值,只与 α 的大小有关.也就是说,这个比值随 α 的确定而唯一确定.这就启发我们,可以利用圆的弧长与半径的关系度量圆心角.
A
B
O
α
图 5.1-10
P
P1
Q
Q1
二、知识讲解
A
B
O
1 rad
图 5.1-11
1
二、知识讲解
角度制、弧度制都是角的度量制,它们之间应该可以换算.如何换算呢?
探究
其中,α 的正负由角 α 的终边的旋转方向决定,即逆时针旋转为正,顺时针旋转为负.当角的终边旋转一周后继续旋转,就可以得到弧度数大于 2π 或小于 -2π 的角.这样就可以得到弧度为任意大小的角.
一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是 0.
二、知识讲解
二、知识讲解
一般地,只需根据
180°=π rad
就可以进行弧度与角度的换算了.
二、知识讲解
1.178 097 245.
因此,67°30′≈1.178 rad.
二、知识讲解
例5 将 3.14 rad 换算成角度(用度数表示,精确到 0.001).
解:利用计算器有
179.908 747 7.
因此,3.14 rad≈179.909°.
二、知识讲解
360°
150°
135°
度
弧度
45°
30°
120°
π
0°
二、知识讲解
角的概念推广后,在弧度制下,角的集合与实数集 R 之间建立起一一对应的关系:每一个角都有唯一的一个实数(等于这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应(图 5.1-12).
图 5.1-12
正角
零角
正实数
负角
负实数
0
二、知识讲解
二、知识讲解
三、小结
弧度制
正角负角零角
象限角
任意角
角的集合与实数集一一对应
终边相同的角:β=α+k · 360°,k∈Z
弧度的概念
弧度公式
弧度与角度的换算
180°=π rad
1.在 0°~360° 范围内,找出与下列各角终边相同的角,并指出它们是第几象限角:
(1)-54°18′;(2)395°8′;(3)-1 190°30′.
答案:(1)305°42′,第四象限角.(2)35°8′,第一象限角.(3)249°30′,第三象限角.
四、练习
2.写出与下列各角终边相同的角的集合,并找出集合中适合不等式 -720°≤β<360° 的元素 β:
(1)1 303°18′;(2)-225°.
答案:(1){β | β=1 303°18′+k · 360°,k∈Z},-496°42′,-136°42′,223°18′.(2){β | β=-225°+k · 360°,k∈Z},-585°,-225°,135°.
四、练习
四、练习
四、练习
谢谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
