人教A版(2019)高中数学必修第一册 2.3 二次函数与一元二次方程、不等式 课件(共29张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第一册 2.3 二次函数与一元二次方程、不等式 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 968.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 10:38:10 | ||
图片预览






文档简介
(共29张PPT)
2.3 二次函数与一元二次方
程、不等式
第二章 一元二次函数、方程和不等式
目录
二、知识讲解
三、小结
四、练习
一、上节回溯
五、本章知识结构
一、上节回溯
应用
定义
基本不等式
几何解释
证明方法
1.一元二次不等式
二、知识讲解
问题 园艺师打算在绿地上用栅栏围一个矩形区域种植花卉.若栅栏的长度是 24 m,围成的矩形区域的面积要大于 20 m2,则这个矩形的边长为多少米?
设这个矩形的一条边长为 x m,则另一条边长为 (12-x) m.由题意,得(12-x)x>20,其中 x∈{x | 0x2-12x+20<0,x∈{x | 0求得不等式 ① 的解集,就得到了问题的答案.
二、知识讲解
一般地,我们把只含有一个未知数,并且未知数的最高次数是 2 的不等式,称为一元二次不等式(quadric inequality in one unknown).一元二次不等式的一般形式是
ax2+bx+c>0 或 ax2+bx+c<0,
其中 a,b,c 均为常数,a≠0.
1.一元二次不等式
二、知识讲解
在初中,我们学习了从一次函数的观点看一元一次方程、一元一次不等式的思想方法.类似地,能否从二次函数的观点看一元二次不等式,进而得到一元二次不等式的求解方法呢?
?
思考
2.一元二次不等式的求解方法
二、知识讲解
下面,我们先考察一元二次不等式 x2-12x+20<0 与二次函数 y=x2-12x+20 之间的关系.
y=x2-12x+20
y
x
O
15
2
5
10
20
5
10
-5
-10
-15
如图,在平面直角坐标系中画出二次函数 y=x2-12x+20 的图象,图象与 x 轴有两个交点.我们知道,这两个交点的横坐标就是方程 x2-12x+20=0 的两个实数根 x1=2,x2=10,因此二次函数 y=x2-12x+20 与 x 轴的两个交点是 (2,0) 和 (10,0).
2.一元二次不等式的求解方法
二、知识讲解
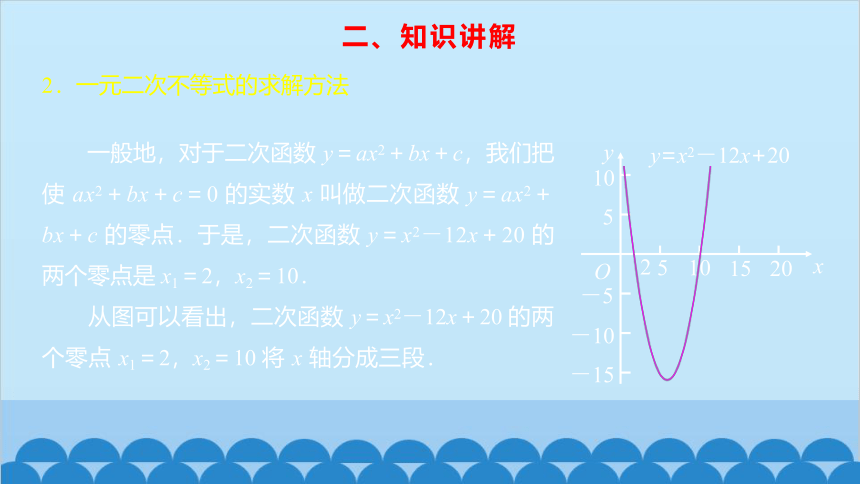
一般地,对于二次函数 y=ax2+bx+c,我们把使 ax2+bx+c=0 的实数 x 叫做二次函数 y=ax2+bx+c 的零点.于是,二次函数 y=x2-12x+20 的两个零点是 x1=2,x2=10.
从图可以看出,二次函数 y=x2-12x+20 的两个零点 x1=2,x2=10 将 x 轴分成三段.
y=x2-12x+20
y
x
O
15
2
5
10
20
5
10
-5
-10
-15
2.一元二次不等式的求解方法
二、知识讲解
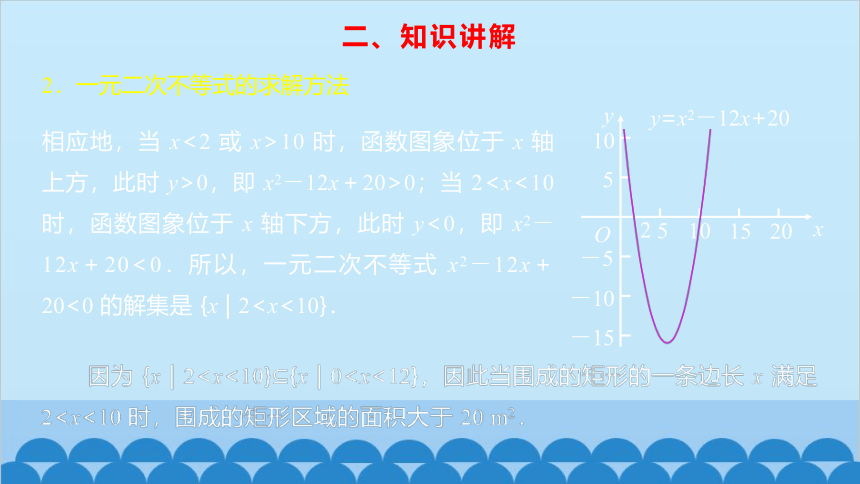
相应地,当 x<2 或 x>10 时,函数图象位于 x 轴上方,此时 y>0,即 x2-12x+20>0;当 2y=x2-12x+20
y
x
O
15
2
5
10
20
5
10
-5
-10
-15
2.一元二次不等式的求解方法
二、知识讲解
2.一元二次不等式的求解方法
二、知识讲解
二次函数与一元二次方程、不等式的解的对应关系
O
y= ax2+bx+c (a>0)
的图象
ax2+bx+c=0 (a>0)
的根
ax2+bx+c>0 (a>0)
的解集
ax2+bx+c<0 (a>0)
的解集
有两个不相等的实数
根 x1,x2 (x1
没有实根
{ x | xx2 }
R
{ x | x1x
x
x
y
y
y
O
O
x1
x2
x1=x2
二、知识讲解
例1 求不等式 x2-5x+6>0 的解集.
分析:因为方程 x2-5x+6=0 的根是函数 y=x2-5x+6 的零点,所以先求出 x2-5x+6=0 的根,再根据函数图象得到 x2-5x+6>0 的解集.
y=x2-5x+6
y
x
O
3
-1
1
2
4
3
4
2
1
-1
5
6
2.一元二次不等式的求解方法
二、知识讲解
例2 求不等式 9x2-6x+1>0 的解集.
y=9x2-6x+1
y
x
O
0.6
0.2
0.4
0.3
0.4
0.2
0.1
0.5
0.6
2.一元二次不等式的求解方法
二、知识讲解
例3 求不等式 -x2+2x-3>0 的解集.
4
y=x2-2x+3
y
x
O
-2
2
4
3
2
1
5
6
现在,你能解决第 2.1 节的“问题 2” 了吗?
2.一元二次不等式的求解方法
二、知识讲解
利用框图可以清晰地表示求解一元二次不等式的过程.这里,我们以求解可化成 ax2+bx+c>0(a>0) 形式的不等式为例,用框图表示其求解过程.
2.一元二次不等式的求解方法
二、知识讲解
将原不等式化成 ax2+bx+c>0(a>0) 的形式
方程 ax2+bx+c=0 有
两个不相等的实数根,
解得 x1,x2 (x1
方程 ax2+bx+c=0 没有实数根
原不等式的解集为{ x | xx2 }
原不等式的解集为 R
二、知识讲解
利用一元二次不等式可以解决一些实际问题,下面看两个例子.
例4 一家车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量 x(单位:辆)与创造的价值 y(单位:元)之间有如下的关系:
y=-20x2+2 200x.
若这家工厂希望在一个星期内利用这条流水线创收 60 000 元以上,则在一个星期内大约应该生产多少辆摩托车?
3.一元二次不等式的应用
二、知识讲解
二、知识讲解
画出二次函数 y=x2-110x+3 000 的图象,结合图象得不等式 x2-110x+3 000<0 的解集为 {x | 50 因为 x 只能取整数值,所以当这条流水线在一周内生产的摩托车数量在 51~59 辆时,这家工厂能够获得 60 000元以上的收益.
50
y=x2-110x+3 000
y
x
O
60
20
40
30
40
20
10
50
10
30
二、知识讲解
3.一元二次不等式的应用
二、知识讲解
二、知识讲解
画出二次函数 s=v2+9v-7 110 的图象,结合图象得不等式的解集为 {v | vv2},从而原不等式的解集为 {v | vv2}.
因为车速 v>0,所以 v>v2.而 79.9s=v2+9v-7 110
s
v
O
v2
v1
类似地,第 2.1 节的不等式①经移项整理,得 2x2-13x+20≤0.用上述方法解这个不等式,得 {x | 2.5≤x≤4}.所以,当每本杂志的定价不低于 2.5 元且不超过 4 元时,提价后的销售总收入不低于 20 万元.
三、小结
解法
定义
一元二次不等式
ax2+bx+c>0 或 ax2+bx+c<0(a≠0)
应用
一元二次方程
ax2+bx+c=0(a≠0)
二次函数
y=ax2+bx+c(a≠0)
四、练习
四、练习
四、练习
5.某网店销售一批新款削笔器,每个削笔器的最低售价为 15 元.若按最低售价销售,每天能卖出 30 个;若一个削笔器的售价每提高 1 元,日销售量将减少 2 个.为了使这批削笔器每天获得 400 元以上的销售收入,应怎样制定这批削笔器的销售价格?
答案:设每个削笔器的售价为 x 元,则 15≤x<20.
四、练习
五、本章知识结构
不等关系
方程
一元二次方程
不等式
等式的性质
相等关系
一元二次不等式
二次函数
不等式的性质
基本不等式
谢谢观看
2.3 二次函数与一元二次方
程、不等式
第二章 一元二次函数、方程和不等式
目录
二、知识讲解
三、小结
四、练习
一、上节回溯
五、本章知识结构
一、上节回溯
应用
定义
基本不等式
几何解释
证明方法
1.一元二次不等式
二、知识讲解
问题 园艺师打算在绿地上用栅栏围一个矩形区域种植花卉.若栅栏的长度是 24 m,围成的矩形区域的面积要大于 20 m2,则这个矩形的边长为多少米?
设这个矩形的一条边长为 x m,则另一条边长为 (12-x) m.由题意,得(12-x)x>20,其中 x∈{x | 0
二、知识讲解
一般地,我们把只含有一个未知数,并且未知数的最高次数是 2 的不等式,称为一元二次不等式(quadric inequality in one unknown).一元二次不等式的一般形式是
ax2+bx+c>0 或 ax2+bx+c<0,
其中 a,b,c 均为常数,a≠0.
1.一元二次不等式
二、知识讲解
在初中,我们学习了从一次函数的观点看一元一次方程、一元一次不等式的思想方法.类似地,能否从二次函数的观点看一元二次不等式,进而得到一元二次不等式的求解方法呢?
?
思考
2.一元二次不等式的求解方法
二、知识讲解
下面,我们先考察一元二次不等式 x2-12x+20<0 与二次函数 y=x2-12x+20 之间的关系.
y=x2-12x+20
y
x
O
15
2
5
10
20
5
10
-5
-10
-15
如图,在平面直角坐标系中画出二次函数 y=x2-12x+20 的图象,图象与 x 轴有两个交点.我们知道,这两个交点的横坐标就是方程 x2-12x+20=0 的两个实数根 x1=2,x2=10,因此二次函数 y=x2-12x+20 与 x 轴的两个交点是 (2,0) 和 (10,0).
2.一元二次不等式的求解方法
二、知识讲解
一般地,对于二次函数 y=ax2+bx+c,我们把使 ax2+bx+c=0 的实数 x 叫做二次函数 y=ax2+bx+c 的零点.于是,二次函数 y=x2-12x+20 的两个零点是 x1=2,x2=10.
从图可以看出,二次函数 y=x2-12x+20 的两个零点 x1=2,x2=10 将 x 轴分成三段.
y=x2-12x+20
y
x
O
15
2
5
10
20
5
10
-5
-10
-15
2.一元二次不等式的求解方法
二、知识讲解
相应地,当 x<2 或 x>10 时,函数图象位于 x 轴上方,此时 y>0,即 x2-12x+20>0;当 2
y
x
O
15
2
5
10
20
5
10
-5
-10
-15
2.一元二次不等式的求解方法
二、知识讲解
2.一元二次不等式的求解方法
二、知识讲解
二次函数与一元二次方程、不等式的解的对应关系
O
y= ax2+bx+c (a>0)
的图象
ax2+bx+c=0 (a>0)
的根
ax2+bx+c>0 (a>0)
的解集
ax2+bx+c<0 (a>0)
的解集
有两个不相等的实数
根 x1,x2 (x1
没有实根
{ x | x
R
{ x | x1
x
x
y
y
y
O
O
x1
x2
x1=x2
二、知识讲解
例1 求不等式 x2-5x+6>0 的解集.
分析:因为方程 x2-5x+6=0 的根是函数 y=x2-5x+6 的零点,所以先求出 x2-5x+6=0 的根,再根据函数图象得到 x2-5x+6>0 的解集.
y=x2-5x+6
y
x
O
3
-1
1
2
4
3
4
2
1
-1
5
6
2.一元二次不等式的求解方法
二、知识讲解
例2 求不等式 9x2-6x+1>0 的解集.
y=9x2-6x+1
y
x
O
0.6
0.2
0.4
0.3
0.4
0.2
0.1
0.5
0.6
2.一元二次不等式的求解方法
二、知识讲解
例3 求不等式 -x2+2x-3>0 的解集.
4
y=x2-2x+3
y
x
O
-2
2
4
3
2
1
5
6
现在,你能解决第 2.1 节的“问题 2” 了吗?
2.一元二次不等式的求解方法
二、知识讲解
利用框图可以清晰地表示求解一元二次不等式的过程.这里,我们以求解可化成 ax2+bx+c>0(a>0) 形式的不等式为例,用框图表示其求解过程.
2.一元二次不等式的求解方法
二、知识讲解
将原不等式化成 ax2+bx+c>0(a>0) 的形式
方程 ax2+bx+c=0 有
两个不相等的实数根,
解得 x1,x2 (x1
方程 ax2+bx+c=0 没有实数根
原不等式的解集为{ x | x
原不等式的解集为 R
二、知识讲解
利用一元二次不等式可以解决一些实际问题,下面看两个例子.
例4 一家车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量 x(单位:辆)与创造的价值 y(单位:元)之间有如下的关系:
y=-20x2+2 200x.
若这家工厂希望在一个星期内利用这条流水线创收 60 000 元以上,则在一个星期内大约应该生产多少辆摩托车?
3.一元二次不等式的应用
二、知识讲解
二、知识讲解
画出二次函数 y=x2-110x+3 000 的图象,结合图象得不等式 x2-110x+3 000<0 的解集为 {x | 50
50
y=x2-110x+3 000
y
x
O
60
20
40
30
40
20
10
50
10
30
二、知识讲解
3.一元二次不等式的应用
二、知识讲解
二、知识讲解
画出二次函数 s=v2+9v-7 110 的图象,结合图象得不等式的解集为 {v | v
因为车速 v>0,所以 v>v2.而 79.9
s
v
O
v2
v1
类似地,第 2.1 节的不等式①经移项整理,得 2x2-13x+20≤0.用上述方法解这个不等式,得 {x | 2.5≤x≤4}.所以,当每本杂志的定价不低于 2.5 元且不超过 4 元时,提价后的销售总收入不低于 20 万元.
三、小结
解法
定义
一元二次不等式
ax2+bx+c>0 或 ax2+bx+c<0(a≠0)
应用
一元二次方程
ax2+bx+c=0(a≠0)
二次函数
y=ax2+bx+c(a≠0)
四、练习
四、练习
四、练习
5.某网店销售一批新款削笔器,每个削笔器的最低售价为 15 元.若按最低售价销售,每天能卖出 30 个;若一个削笔器的售价每提高 1 元,日销售量将减少 2 个.为了使这批削笔器每天获得 400 元以上的销售收入,应怎样制定这批削笔器的销售价格?
答案:设每个削笔器的售价为 x 元,则 15≤x<20.
四、练习
五、本章知识结构
不等关系
方程
一元二次方程
不等式
等式的性质
相等关系
一元二次不等式
二次函数
不等式的性质
基本不等式
谢谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
