人教A版(2019)高中数学必修第一册 4.2指数函数 课件(共35张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第一册 4.2指数函数 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 10:39:22 | ||
图片预览










文档简介
(共35张PPT)
4.2 指数函数
第四章 指数函数与对数函数
目录
二、知识讲解
三、小结
四、练习
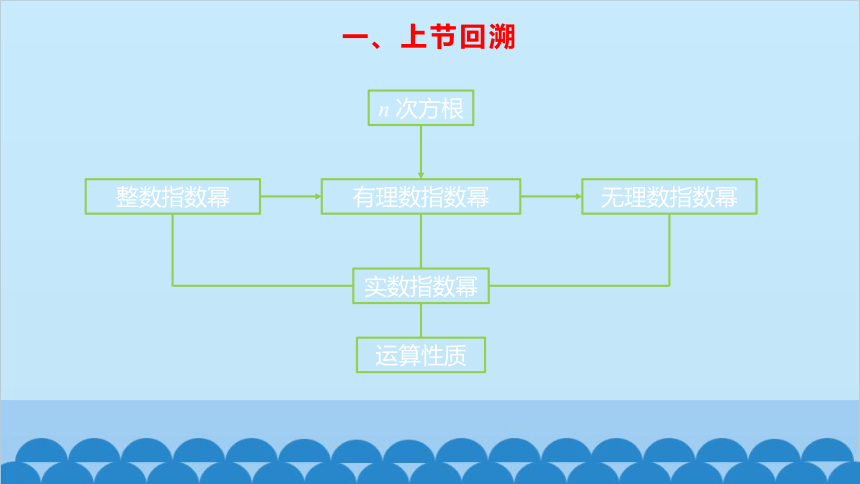
一、上节回溯
一、上节回溯
有理数指数幂
n 次方根
整数指数幂
无理数指数幂
实数指数幂
运算性质
二、知识讲解
对于幂 ax (a>0),我们已经把指数 x 的范围拓展到了实数.上一章学习了函数的概念和基本性质,通过对幂函数的研究,进一步了解了研究一类函数的过程和方法.下面继续研究其他类型的基本初等函数.
二、知识讲解
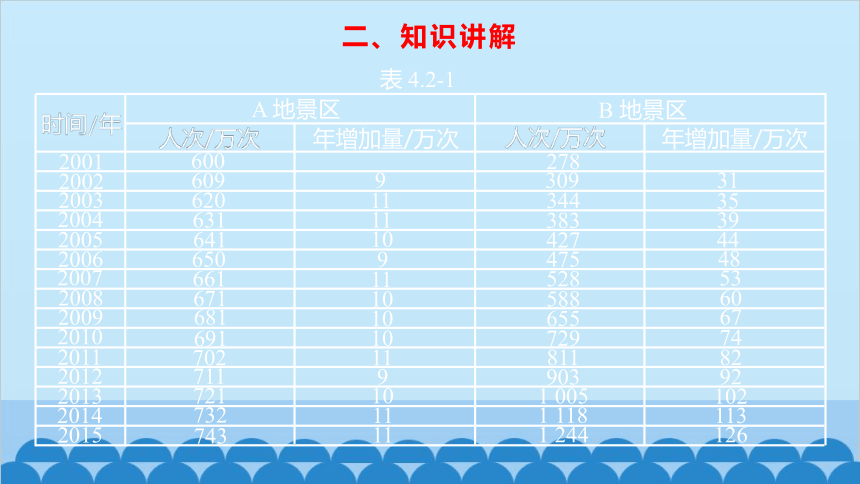
问题1 随着中国经济高速增长,人民生活水平不断提高,旅游成了越来越多家庭的重要生活方式.由于旅游人数不断增加,A,B 两地景区自2001 年起采取了不同的应对措施,A 地提高了景区门票价格,而 B 地则取消了景区门票.表 4.2-1 给出了 A,B 两地景区 2001 年至 2015 年的游客人次以及逐年增加量.
4.2.1 指数函数的概念
二、知识讲解
309
11
702
2003
A 地景区
年增加量/万次
2009
2005
609
2006
661
2008
2007
631
2015
2001
2002
2004
641
620
600
650
2011
2010
2012
2014
2013
表 4.2-1
B 地景区
年增加量/万次
671
681
691
711
721
732
743
10
11
9
9
11
10
10
10
11
9
10
11
11
344
383
278
427
475
528
588
655
729
811
903
1 005
1 118
1 244
44
35
31
48
53
60
67
74
82
92
102
113
126
39
二、知识讲解
比较两地景区游客人次的变化情况,你发现了怎样的变化规律?
为了有利于观察规律,根据表 4.2-1,分别画出 A,B 两地景区采取不同措施后的 15 年游客人次的图象(图 4.2-1 和图 4.2-2).
2003
2001
2005
2007
2009
2011
2013
2015
时间/年
300
500
700
900
1100
1300
人次/万次
图 4.2-1
2003
2001
2005
2007
2009
2011
2013
2015
时间/年
300
500
700
900
1100
1300
人次/万次
图 4.2-2
二、知识讲解
观察图象和表格,可以发现,A 地景区的游客人次近似于直线上升(线性增长),年增加量大致相等(约为 10 万次);B 地景区的游客人次则是非线性增长,年增加量越来越大,但从图象和年增加量都难以看出变化规律.
探究
二、知识讲解
二、知识讲解
二、知识讲解
x 年后,游客人次是 2001 年的 1.11x 倍.
如果设经过 x 年后的游客人次为 2001 年的 y 倍,那么
y=1.11x (x∈[0,+∞)). ①
这是一个函数,其中指数 x 是自变量.
二、知识讲解
问题2 当生物死亡后,它机体内原有的碳 14 含量会按确定的比率衰减(称为衰减率),大约每经过 5 730 年衰减为原来的一半,这个时间称为“半衰期”.按照上述变化规律,生物体内碳 14 含量与死亡年数之间有怎样的关系?
设死亡生物体内碳 14 含量的年衰减率为 p,如果把刚死亡的生物体内碳 14 含量看成 1 个单位,那么
死亡 1 年后,生物体内碳 14 含量为 (1-p)1;
死亡 2 年后,生物体内碳 14 含量为 (1-p)2;
死亡 3 年后,生物体内碳 14 含量为 (1-p)3;
二、知识讲解
二、知识讲解
二、知识讲解
二、知识讲解
例2 (1)在问题 1 中,如果平均每位游客出游一次可给当地带来 1 000 元门票之外的收入,A 地景区的门票价格为 150 元,比较这 15 年间 A,B 两地旅游收入变化情况.
(2)在问题 2 中,某生物死亡 10 000 年后,它体内碳 14 的含量衰减为原来的百分之几?
解:(1)设经过 x 年,游客给 A,B 两地带来的收入分别为 f (x) 和 g (x),则
f (x)=1 150×(10x+600),
g (x)=1 000×278×1.11x.
利用计算工具可得,
二、知识讲解
当 x=0 时,f (0)-g (0)=412 000.
当 x≈10.22 时,f (10.22)≈g (10.22).
结合图 4.2-3 可知:
当 x<10.22 时,f (x)>g (x),
当 x>10.22 时,f (x) 当 x=14 时,g (14)-f (14)≈347 303.
这说明,在 2001 年,游客给 A 地带来的收入比 B 地多 412 000 万元;随后 10 年,虽然 f (x)>g (x),但 g (x) 的增长速度大于 f (x);
O
x
y
2
20
40
4
60
6
80
8
100
10
140
12
f (x)
14
120
16
g (x)
图 4.2-3
二、知识讲解
二、知识讲解
在实际问题中,经常会遇到类似于例 2(1)的指数增长模型:设原有量为 N,每次的增长率为 p,经过 x 次增长,该量增长到 y,则 y=N(1+p)x (x∈N).形如 y=kax (k∈R,且 k≠0,a>0,且 a≠1) 的函数是刻画指数增长或指数衰减变化规律的非常有用的函数模型.
二、知识讲解
下面我们类比研究幂函数性质的过程和方法,进一步研究指数函数.首先画出指数函数的图象,然后借助图象研究指数函数的性质.
先从简单的函数 y=2x 开始.
请同学们完成 x,y 的对应值表 4.2-2,并用描点法画出函数 y=2x 的图象(图 4.2-4).
4.2.2 指数函数的图象和性质
二、知识讲解
为了得到指数函数 y=ax (a>0,且 a≠1) 的性质,我们还需要画出更多的具体指数函数的图象进行观察.
x
y
-1.5
-2
-1
-0.5
0.5
0
1
1.5
2
0.35
0.71
1.41
2.83
表 4.2-2
x
y
O
图 4.2-4
-1
-2
-3
2
1
3
1
2
3
4
5
6
7
8
y=2x
二、知识讲解
探究
二、知识讲解
y
x
O
y=2x
P
P1
1
图 4.2-5
二、知识讲解
选取底数 a (a>0,且 a≠1) 的若干个不同的值,在同一直角坐标系内画出相应的指数函数的图象.观察这些图象的位置、公共点和变化趋势,它们有哪些共性?由此你能概括出指数函数 y=ax (a>0,且 a≠1) 的值域和性质吗?
探究
二、知识讲解
如图 4.2-6,选取底数 a 的若干值,用信息技术画图,发现指数函数 y=ax的图象按底数 a 的取值,可分为 01 两种类型.因此,指数函数的性质也可以分 01 两种情况进行研究.
y
x
O
y=2x
1
图 4.2-6
y=3x
y=4x
二、知识讲解
一般地,指数函数的图象和性质如表 4.2-3 所示.
x
y
O
y=1
y=ax
(0,1)
x
y
O
y=1
y=ax
(0,1)
定义域
图象
值域
性质
(2)减函数
(1)过定点 (0,1),即 x=0 时,y=1
(2)增函数
(0,+∞)
R
0a>1
表 4.2-3
二、知识讲解
二、知识讲解
例4 如图 4.2-7,某城市人口呈指数增长.
(1)根据图象,估计该城市人口每翻一番所需的时间(倍增期);
(2)该城市人口从 80 万人开始,经过 20 年会增长到多少万人?
分析:(1)因为该城市人口呈指数增长,而同一指数函数的倍增期是相同的,所以可以从图象中选取适当的点计算倍增期.(2)要计算 20 年后的人口数,关键是要找到 20 年与倍增期的数量关系.
x/年
y/万人
20
O
10
30
40
50
60
70
80
20
10
30
40
50
60
70
80
图 4.2-7
三、小结
图象
指数函数
概念
性质
四、练习
四、练习
四、练习
y
x
O
1
y=3x
四、练习
5.体内癌细胞初期增加得很缓慢,但到了晚期就急剧增加,画一幅能反映体内癌细胞数量随时间变化的示意图.
答案:可用指数函数 S=S0at 来刻画体内癌细胞数量 S 随时间 t 变化的规律,其中初始量 S0>0,增长比例 a>1,t≥0.
四、练习
S
t
O
S0
S=S0at
谢谢观看
4.2 指数函数
第四章 指数函数与对数函数
目录
二、知识讲解
三、小结
四、练习
一、上节回溯
一、上节回溯
有理数指数幂
n 次方根
整数指数幂
无理数指数幂
实数指数幂
运算性质
二、知识讲解
对于幂 ax (a>0),我们已经把指数 x 的范围拓展到了实数.上一章学习了函数的概念和基本性质,通过对幂函数的研究,进一步了解了研究一类函数的过程和方法.下面继续研究其他类型的基本初等函数.
二、知识讲解
问题1 随着中国经济高速增长,人民生活水平不断提高,旅游成了越来越多家庭的重要生活方式.由于旅游人数不断增加,A,B 两地景区自2001 年起采取了不同的应对措施,A 地提高了景区门票价格,而 B 地则取消了景区门票.表 4.2-1 给出了 A,B 两地景区 2001 年至 2015 年的游客人次以及逐年增加量.
4.2.1 指数函数的概念
二、知识讲解
309
11
702
2003
A 地景区
年增加量/万次
2009
2005
609
2006
661
2008
2007
631
2015
2001
2002
2004
641
620
600
650
2011
2010
2012
2014
2013
表 4.2-1
B 地景区
年增加量/万次
671
681
691
711
721
732
743
10
11
9
9
11
10
10
10
11
9
10
11
11
344
383
278
427
475
528
588
655
729
811
903
1 005
1 118
1 244
44
35
31
48
53
60
67
74
82
92
102
113
126
39
二、知识讲解
比较两地景区游客人次的变化情况,你发现了怎样的变化规律?
为了有利于观察规律,根据表 4.2-1,分别画出 A,B 两地景区采取不同措施后的 15 年游客人次的图象(图 4.2-1 和图 4.2-2).
2003
2001
2005
2007
2009
2011
2013
2015
时间/年
300
500
700
900
1100
1300
人次/万次
图 4.2-1
2003
2001
2005
2007
2009
2011
2013
2015
时间/年
300
500
700
900
1100
1300
人次/万次
图 4.2-2
二、知识讲解
观察图象和表格,可以发现,A 地景区的游客人次近似于直线上升(线性增长),年增加量大致相等(约为 10 万次);B 地景区的游客人次则是非线性增长,年增加量越来越大,但从图象和年增加量都难以看出变化规律.
探究
二、知识讲解
二、知识讲解
二、知识讲解
x 年后,游客人次是 2001 年的 1.11x 倍.
如果设经过 x 年后的游客人次为 2001 年的 y 倍,那么
y=1.11x (x∈[0,+∞)). ①
这是一个函数,其中指数 x 是自变量.
二、知识讲解
问题2 当生物死亡后,它机体内原有的碳 14 含量会按确定的比率衰减(称为衰减率),大约每经过 5 730 年衰减为原来的一半,这个时间称为“半衰期”.按照上述变化规律,生物体内碳 14 含量与死亡年数之间有怎样的关系?
设死亡生物体内碳 14 含量的年衰减率为 p,如果把刚死亡的生物体内碳 14 含量看成 1 个单位,那么
死亡 1 年后,生物体内碳 14 含量为 (1-p)1;
死亡 2 年后,生物体内碳 14 含量为 (1-p)2;
死亡 3 年后,生物体内碳 14 含量为 (1-p)3;
二、知识讲解
二、知识讲解
二、知识讲解
二、知识讲解
例2 (1)在问题 1 中,如果平均每位游客出游一次可给当地带来 1 000 元门票之外的收入,A 地景区的门票价格为 150 元,比较这 15 年间 A,B 两地旅游收入变化情况.
(2)在问题 2 中,某生物死亡 10 000 年后,它体内碳 14 的含量衰减为原来的百分之几?
解:(1)设经过 x 年,游客给 A,B 两地带来的收入分别为 f (x) 和 g (x),则
f (x)=1 150×(10x+600),
g (x)=1 000×278×1.11x.
利用计算工具可得,
二、知识讲解
当 x=0 时,f (0)-g (0)=412 000.
当 x≈10.22 时,f (10.22)≈g (10.22).
结合图 4.2-3 可知:
当 x<10.22 时,f (x)>g (x),
当 x>10.22 时,f (x)
这说明,在 2001 年,游客给 A 地带来的收入比 B 地多 412 000 万元;随后 10 年,虽然 f (x)>g (x),但 g (x) 的增长速度大于 f (x);
O
x
y
2
20
40
4
60
6
80
8
100
10
140
12
f (x)
14
120
16
g (x)
图 4.2-3
二、知识讲解
二、知识讲解
在实际问题中,经常会遇到类似于例 2(1)的指数增长模型:设原有量为 N,每次的增长率为 p,经过 x 次增长,该量增长到 y,则 y=N(1+p)x (x∈N).形如 y=kax (k∈R,且 k≠0,a>0,且 a≠1) 的函数是刻画指数增长或指数衰减变化规律的非常有用的函数模型.
二、知识讲解
下面我们类比研究幂函数性质的过程和方法,进一步研究指数函数.首先画出指数函数的图象,然后借助图象研究指数函数的性质.
先从简单的函数 y=2x 开始.
请同学们完成 x,y 的对应值表 4.2-2,并用描点法画出函数 y=2x 的图象(图 4.2-4).
4.2.2 指数函数的图象和性质
二、知识讲解
为了得到指数函数 y=ax (a>0,且 a≠1) 的性质,我们还需要画出更多的具体指数函数的图象进行观察.
x
y
-1.5
-2
-1
-0.5
0.5
0
1
1.5
2
0.35
0.71
1.41
2.83
表 4.2-2
x
y
O
图 4.2-4
-1
-2
-3
2
1
3
1
2
3
4
5
6
7
8
y=2x
二、知识讲解
探究
二、知识讲解
y
x
O
y=2x
P
P1
1
图 4.2-5
二、知识讲解
选取底数 a (a>0,且 a≠1) 的若干个不同的值,在同一直角坐标系内画出相应的指数函数的图象.观察这些图象的位置、公共点和变化趋势,它们有哪些共性?由此你能概括出指数函数 y=ax (a>0,且 a≠1) 的值域和性质吗?
探究
二、知识讲解
如图 4.2-6,选取底数 a 的若干值,用信息技术画图,发现指数函数 y=ax的图象按底数 a 的取值,可分为 0
y
x
O
y=2x
1
图 4.2-6
y=3x
y=4x
二、知识讲解
一般地,指数函数的图象和性质如表 4.2-3 所示.
x
y
O
y=1
y=ax
(0,1)
x
y
O
y=1
y=ax
(0,1)
定义域
图象
值域
性质
(2)减函数
(1)过定点 (0,1),即 x=0 时,y=1
(2)增函数
(0,+∞)
R
0
表 4.2-3
二、知识讲解
二、知识讲解
例4 如图 4.2-7,某城市人口呈指数增长.
(1)根据图象,估计该城市人口每翻一番所需的时间(倍增期);
(2)该城市人口从 80 万人开始,经过 20 年会增长到多少万人?
分析:(1)因为该城市人口呈指数增长,而同一指数函数的倍增期是相同的,所以可以从图象中选取适当的点计算倍增期.(2)要计算 20 年后的人口数,关键是要找到 20 年与倍增期的数量关系.
x/年
y/万人
20
O
10
30
40
50
60
70
80
20
10
30
40
50
60
70
80
图 4.2-7
三、小结
图象
指数函数
概念
性质
四、练习
四、练习
四、练习
y
x
O
1
y=3x
四、练习
5.体内癌细胞初期增加得很缓慢,但到了晚期就急剧增加,画一幅能反映体内癌细胞数量随时间变化的示意图.
答案:可用指数函数 S=S0at 来刻画体内癌细胞数量 S 随时间 t 变化的规律,其中初始量 S0>0,增长比例 a>1,t≥0.
四、练习
S
t
O
S0
S=S0at
谢谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
