黑龙江省齐齐哈尔市齐市第八高级中学2022-2023学年高二上学期9月开学考试数学试题(含答案)
文档属性
| 名称 | 黑龙江省齐齐哈尔市齐市第八高级中学2022-2023学年高二上学期9月开学考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 822.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 11:53:43 | ||
图片预览



文档简介
齐市第八高级中学2022-2023学年高二上学期9月开学考试
数学试题
分值:150分时间:120分钟
一 单选题(本题共8小题,每小题5分,共40分.每题四个选项中只有一个正确选项)
1.已知复数在复平面内对应的点的坐标为,则( )
A. B. C. D.
2.已知是上的偶函数,在上单调递增,且,则下列不等式成立的是( )
A.
B.
C.
D.
3.若,且恒成立,则实数的取值范围是( )
A. B.或
C.或 D.
4.《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”;四个面均为直角三角形的四面体称为“鳌臑”.如图,在堑堵中,,且,下列说法错误的是( )
A.四棱锥为“阳马”
B.四面体为“鳖臑”
C.四棱锥体积的最大值为
D.过A点作于点,过点作于点,则面
5.在中,角的对边分别为,已知三个向量,共线,则的形状为( )
A.等边三角形 B.钝角三角形
C.有一个角是的直角三角形 D.等腰直角三角形
6.若,则事件与的关系正确的是( )
A.事件与互斥 B.事件与对立
C.事件与相互独立 D.事件与既互斥又独立
7.新冠肺炎疫情发生以来,医用口罩成为抗疫急需物资.某医用口罩生产厂家生产三种不同型号的口罩,三种型号的口罩产量之比为.为了提高这三种口罩的质量,用分层抽样的方法抽取一个容量为的样本.在样本中种口罩数量比种口罩数量多40只,比种口罩数量多80只,则( )
A.240 B.280 C.320 D.360
8.灯笼起源于中国的西汉时期,两千多年来,每逢节日人们便会挂起象征美好团圆意义的红灯笼,营造一种喜庆的氛围.如图1,某球形灯笼的轮廓由三部分组成,上下两部分是两个相同的圆柱的侧面,中间是球面的一部分(除去两个球冠).如图2,球冠是由球面被一个平面截得的,垂直于截面的直径被截得的部分叫做球冠的高,若球冠所在球的半径为,球冠的高为,则球冠的面积.已知该灯笼的高为,圆柱的高为,圆柱的底面圆直径为,则围成该灯笼所需布料的面积为( )
A. B. C. D.
二 多选题(本题共4小题,每小题5分,共20分.每小题有多项正确选项,全部选对得5分,有选错的得0分,部分选对得2分)
9.下列说法正确的是( )
A.圆柱的侧面展开图是矩形
B.球面可以看成是一个圆绕着它的直径所在的直线旋转所形成的曲面
C.直角梯形绕它的一腰所在直线旋转一周形成的几何体是圆台
D.圆柱 圆锥 圆台中,平行于底面的截面都是圆面
10.函数的部分图像如图所示,下列说法正确的是( )
A.图像的一条对称轴可能为直线
B.函数的解折式可以为
C.的图像关于点对称
D.在区间上单调递增
11.下列命题中是真命题的有( )
A.有三种个体按的比例分层抽样调查,如果抽取的个体数为9,则样本容量为30
B.一组数据的平均数 众数 中位数相同
C.若甲组数据的方差为5,乙组数据为,则这两组数据中较稳定的是甲
D.某一组样本数据为,则样本数据落在区间内的频率为
12.如图所示是正方体的平面展开图,那么在正方体中( )
A.
B.和所成的角是
C.直线和平面所成的角是
D.如果平面平面,那么直线直线.
三 填空题(本题共4小题,每题5分,共20分)
13.已知向量,若,则__________.
14.在四面体中,,且,则该四面体外接球的表面积为__________.
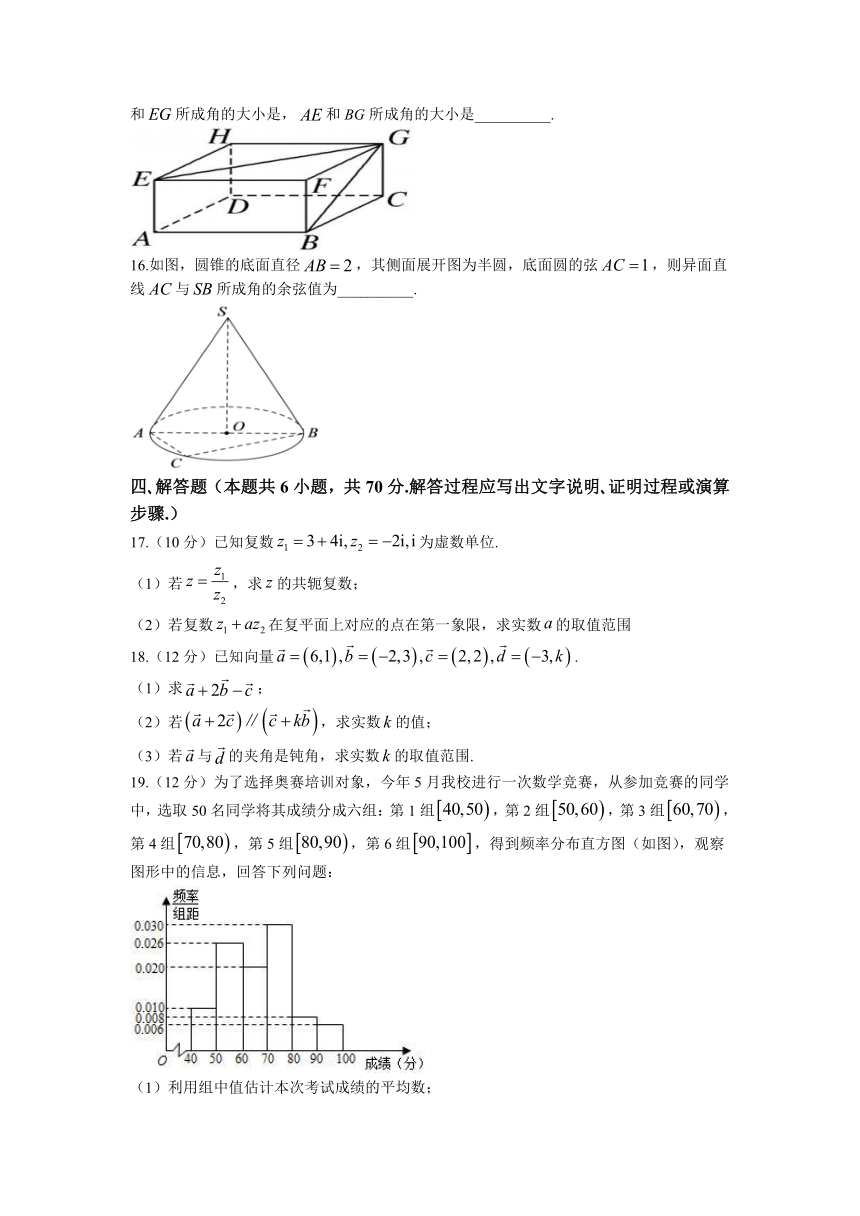
15.如图所示,已知在长方体中,,则和所成角的大小是,和BG所成角的大小是__________.
16.如图,圆锥的底面直径,其侧面展开图为半圆,底面圆的弦,则异面直线与所成角的余弦值为__________.
四 解答题(本题共6小题,共70分.解答过程应写出文字说明 证明过程或演算步骤.)
17.(10分)已知复数为虚数单位.
(1)若,求的共轭复数;
(2)若复数在复平面上对应的点在第一象限,求实数的取值范围
18.(12分)已知向量.
(1)求;
(2)若,求实数的值;
(3)若与的夹角是钝角,求实数的取值范围.
19.(12分)为了选择奥赛培训对象,今年5月我校进行一次数学竞赛,从参加竞赛的同学中,选取50名同学将其成绩分成六组:第1组,第2组,第3组,第4组,第5组,第6组,得到频率分布直方图(如图),观察图形中的信息,回答下列问题:
(1)利用组中值估计本次考试成绩的平均数;
(2)从频率分布直方图中,估计第65百分位数是多少;
(3)已知学生成绩评定等级有优秀 良好 一般三个等级,其中成绩不小于90分时为优秀等级,若从第5组和第6组两组学生中,随机抽取2人,求所抽取的2人中至少1人成绩优秀的概率.
20.(12分)记的内角的对边分别为,已知__________.
在①,②这两个条件中任选一个,补充在上面的横线上,并解答下列问题:
(1)求的大小;
(2)若的面积为,且,求的周长.
21.(12分)已知函数.
(1)求的最小正周期和对称轴方程;
(2)若函数在存在零点,求实数的取值范围.
22.(12分)在四棱锥中,,为正三角形,且平面平面.
(1)求二面角的余弦值;
(2)线段上是否存在一点,使得异面直线和所成的角的余弦值为?若存在,指出点的位置;若不存在,请说明理由.
开学考试答案
一、选择题:
1 2 3 4 5 6 7 8 9 10 11 12
D B A C A C A B ABD BC BD BCD
二、填空题
13. 14. 15.45°;60° 16.
三、解答题
17.(1)由
所以;
(2)由题意,复数,,
,
∵复数在复平面上对应的点在第一象限,
∴解得,
∴实数a的取值范围.
18.(1)因为(6,1),(,3),(2,2),
∴(6,1)+(,6) (2,2)=(0,5).
(2)(10,5),(2 2k,2+3k),
∵,
∴10(2+3k) 5(2 2k)=0,
解得.
(3)与的夹角是钝角,
∴,且,
∵,
且,
解得且.
19.(1)本次考试成绩的平均数为.
(2)因为前3组频率之和为,前4组频率之和为,
所以第百分位数在第4组中,设为,
则,解得.
第百分位数是.
(3)第五组与第六组学生总人数为,
其中第五组有人,记为 ,第六组有人,记为 ,
从中随机抽取人的情况有: 共有种,
其中至少人成绩优秀的情况有种,
所抽取的人中至少人成绩优秀的概率.
20.解①选择①
由题意得.
得,
即.
选择②
由题意得,即.
所以.
即.
(2)由的面积.得.
由,得.
得,即.
故的周长为.
21.解:(1)对于函数6cosx(sinxcosx)sin2x﹣3
=3(sin2x cos2x)=3sin(2x),
故它的最小正周期为π.
令2xkπ,求得x,k∈Z,
故f(x)的对称轴方程为x,k∈Z.
(2)∵函数y=f(x)﹣a在存在零点,即sin(2x),在[,]上有解.
当x∈[,],2x∈[0,],sin(2x)∈[0,1],
∴∈[0,1],∴a∈[0,3].
22.(1)设是中点,为正三角形,
则,平面平面,
面,又∵,
,所以为正三角形,,
建立如图所示空间直角坐标系,则,
于是,,
(1)设平面的法向量为,
由得一个法向量为,
平面的一个法向量为,
设二面角的平面角为,则
由图知为锐角,所以,二面角的余弦值为.
(2)设,则,
,
所以
解得或,所以存在点M为线段PC的三等分点.
数学试题
分值:150分时间:120分钟
一 单选题(本题共8小题,每小题5分,共40分.每题四个选项中只有一个正确选项)
1.已知复数在复平面内对应的点的坐标为,则( )
A. B. C. D.
2.已知是上的偶函数,在上单调递增,且,则下列不等式成立的是( )
A.
B.
C.
D.
3.若,且恒成立,则实数的取值范围是( )
A. B.或
C.或 D.
4.《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”;四个面均为直角三角形的四面体称为“鳌臑”.如图,在堑堵中,,且,下列说法错误的是( )
A.四棱锥为“阳马”
B.四面体为“鳖臑”
C.四棱锥体积的最大值为
D.过A点作于点,过点作于点,则面
5.在中,角的对边分别为,已知三个向量,共线,则的形状为( )
A.等边三角形 B.钝角三角形
C.有一个角是的直角三角形 D.等腰直角三角形
6.若,则事件与的关系正确的是( )
A.事件与互斥 B.事件与对立
C.事件与相互独立 D.事件与既互斥又独立
7.新冠肺炎疫情发生以来,医用口罩成为抗疫急需物资.某医用口罩生产厂家生产三种不同型号的口罩,三种型号的口罩产量之比为.为了提高这三种口罩的质量,用分层抽样的方法抽取一个容量为的样本.在样本中种口罩数量比种口罩数量多40只,比种口罩数量多80只,则( )
A.240 B.280 C.320 D.360
8.灯笼起源于中国的西汉时期,两千多年来,每逢节日人们便会挂起象征美好团圆意义的红灯笼,营造一种喜庆的氛围.如图1,某球形灯笼的轮廓由三部分组成,上下两部分是两个相同的圆柱的侧面,中间是球面的一部分(除去两个球冠).如图2,球冠是由球面被一个平面截得的,垂直于截面的直径被截得的部分叫做球冠的高,若球冠所在球的半径为,球冠的高为,则球冠的面积.已知该灯笼的高为,圆柱的高为,圆柱的底面圆直径为,则围成该灯笼所需布料的面积为( )
A. B. C. D.
二 多选题(本题共4小题,每小题5分,共20分.每小题有多项正确选项,全部选对得5分,有选错的得0分,部分选对得2分)
9.下列说法正确的是( )
A.圆柱的侧面展开图是矩形
B.球面可以看成是一个圆绕着它的直径所在的直线旋转所形成的曲面
C.直角梯形绕它的一腰所在直线旋转一周形成的几何体是圆台
D.圆柱 圆锥 圆台中,平行于底面的截面都是圆面
10.函数的部分图像如图所示,下列说法正确的是( )
A.图像的一条对称轴可能为直线
B.函数的解折式可以为
C.的图像关于点对称
D.在区间上单调递增
11.下列命题中是真命题的有( )
A.有三种个体按的比例分层抽样调查,如果抽取的个体数为9,则样本容量为30
B.一组数据的平均数 众数 中位数相同
C.若甲组数据的方差为5,乙组数据为,则这两组数据中较稳定的是甲
D.某一组样本数据为,则样本数据落在区间内的频率为
12.如图所示是正方体的平面展开图,那么在正方体中( )
A.
B.和所成的角是
C.直线和平面所成的角是
D.如果平面平面,那么直线直线.
三 填空题(本题共4小题,每题5分,共20分)
13.已知向量,若,则__________.
14.在四面体中,,且,则该四面体外接球的表面积为__________.
15.如图所示,已知在长方体中,,则和所成角的大小是,和BG所成角的大小是__________.
16.如图,圆锥的底面直径,其侧面展开图为半圆,底面圆的弦,则异面直线与所成角的余弦值为__________.
四 解答题(本题共6小题,共70分.解答过程应写出文字说明 证明过程或演算步骤.)
17.(10分)已知复数为虚数单位.
(1)若,求的共轭复数;
(2)若复数在复平面上对应的点在第一象限,求实数的取值范围
18.(12分)已知向量.
(1)求;
(2)若,求实数的值;
(3)若与的夹角是钝角,求实数的取值范围.
19.(12分)为了选择奥赛培训对象,今年5月我校进行一次数学竞赛,从参加竞赛的同学中,选取50名同学将其成绩分成六组:第1组,第2组,第3组,第4组,第5组,第6组,得到频率分布直方图(如图),观察图形中的信息,回答下列问题:
(1)利用组中值估计本次考试成绩的平均数;
(2)从频率分布直方图中,估计第65百分位数是多少;
(3)已知学生成绩评定等级有优秀 良好 一般三个等级,其中成绩不小于90分时为优秀等级,若从第5组和第6组两组学生中,随机抽取2人,求所抽取的2人中至少1人成绩优秀的概率.
20.(12分)记的内角的对边分别为,已知__________.
在①,②这两个条件中任选一个,补充在上面的横线上,并解答下列问题:
(1)求的大小;
(2)若的面积为,且,求的周长.
21.(12分)已知函数.
(1)求的最小正周期和对称轴方程;
(2)若函数在存在零点,求实数的取值范围.
22.(12分)在四棱锥中,,为正三角形,且平面平面.
(1)求二面角的余弦值;
(2)线段上是否存在一点,使得异面直线和所成的角的余弦值为?若存在,指出点的位置;若不存在,请说明理由.
开学考试答案
一、选择题:
1 2 3 4 5 6 7 8 9 10 11 12
D B A C A C A B ABD BC BD BCD
二、填空题
13. 14. 15.45°;60° 16.
三、解答题
17.(1)由
所以;
(2)由题意,复数,,
,
∵复数在复平面上对应的点在第一象限,
∴解得,
∴实数a的取值范围.
18.(1)因为(6,1),(,3),(2,2),
∴(6,1)+(,6) (2,2)=(0,5).
(2)(10,5),(2 2k,2+3k),
∵,
∴10(2+3k) 5(2 2k)=0,
解得.
(3)与的夹角是钝角,
∴,且,
∵,
且,
解得且.
19.(1)本次考试成绩的平均数为.
(2)因为前3组频率之和为,前4组频率之和为,
所以第百分位数在第4组中,设为,
则,解得.
第百分位数是.
(3)第五组与第六组学生总人数为,
其中第五组有人,记为 ,第六组有人,记为 ,
从中随机抽取人的情况有: 共有种,
其中至少人成绩优秀的情况有种,
所抽取的人中至少人成绩优秀的概率.
20.解①选择①
由题意得.
得,
即.
选择②
由题意得,即.
所以.
即.
(2)由的面积.得.
由,得.
得,即.
故的周长为.
21.解:(1)对于函数6cosx(sinxcosx)sin2x﹣3
=3(sin2x cos2x)=3sin(2x),
故它的最小正周期为π.
令2xkπ,求得x,k∈Z,
故f(x)的对称轴方程为x,k∈Z.
(2)∵函数y=f(x)﹣a在存在零点,即sin(2x),在[,]上有解.
当x∈[,],2x∈[0,],sin(2x)∈[0,1],
∴∈[0,1],∴a∈[0,3].
22.(1)设是中点,为正三角形,
则,平面平面,
面,又∵,
,所以为正三角形,,
建立如图所示空间直角坐标系,则,
于是,,
(1)设平面的法向量为,
由得一个法向量为,
平面的一个法向量为,
设二面角的平面角为,则
由图知为锐角,所以,二面角的余弦值为.
(2)设,则,
,
所以
解得或,所以存在点M为线段PC的三等分点.
同课章节目录
