四川省遂宁市涪江高级中学校2022-2023学年高三上学期9月开学考试数学(理)试题(含答案)
文档属性
| 名称 | 四川省遂宁市涪江高级中学校2022-2023学年高三上学期9月开学考试数学(理)试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 334.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 00:00:00 | ||
图片预览


文档简介
涪江高级中学校2022-2023学年高三上学期9月开学考试
数学试题(理)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知是虚数单位,若复数满足:,则复数( )
A. B. C. D.
2. 已知,,且,则的最小值为( )
A. 2 B. 4 C. 6 D. 8
3. 在集合和中各取一个数字组成一个两位数,则这个两位数能被4整除的概率为( )
A. B. C. D.
4. 已知实数,,满足,,,则实数,,的大小关系为( )
A. B. C. D.
5. 在中,“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
6. 月形是一种特殊的平面图形,指有相同的底,且在底的同一侧的两个弓形所围成的图形.月形中的一种特殊的情形是镰刀形,即由半圆和弓形所围成的图形(如下图),若半圆的半径与弓形所在圆的半径之比为,现向半圆内随机取一点,则取到镰刀形中的一点的概率为( )
A. B. C. D.
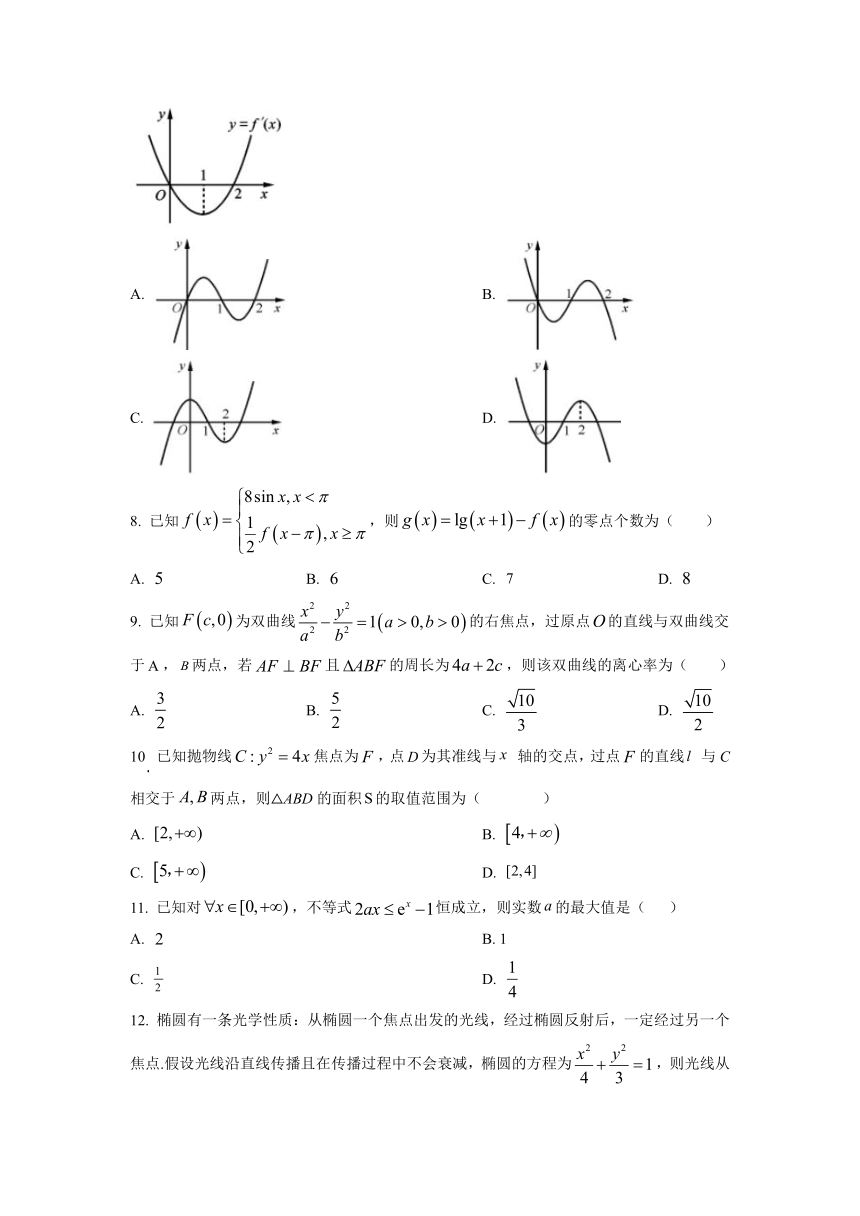
7. 设是函数的导函数,的图像如图所示,则的图像最有可能的是( )
A. B.
C. D.
8. 已知,则的零点个数为( )
A. B. C. D.
9. 已知为双曲线的右焦点,过原点的直线与双曲线交于,两点,若且的周长为,则该双曲线的离心率为( )
A. B. C. D.
10 已知抛物线焦点为,点为其准线与 轴的交点,过点的直线 与C相交于两点,则△ABD的面积的取值范围为( )
A. B.
C. D.
11. 已知对,不等式恒成立,则实数的最大值是( )
A. B. 1
C. D.
12. 椭圆有一条光学性质:从椭圆一个焦点出发的光线,经过椭圆反射后,一定经过另一个焦点.假设光线沿直线传播且在传播过程中不会衰减,椭圆的方程为,则光线从椭圆一个焦点出发,到首次回到该焦点所经过的路程不可能为( )
A. 2 B. 4 C. 6 D. 8
二、填空题:本题共4小题,每小题5分,共20分.
13. 曲线在点处的切线方程为__________.
14. 已知圆:与直线:相交于、两点,且,则实数______.
15. 若函数为定义在上的奇函数,当时,,则不等式的解集为______.
16. 已知x,,满足,给出下列四个结论:①;②;③;④.其中一定成立的结论是______(写出所有成立结论的编号).
三、解答题:本题共70分.解答应写出文字说明、证明过程或演算步骤.
17. 设命题:函数在区间上单调递减;命题:对恒成立.如果命题“且”为假命题,求的取值范围.
18. 在直角坐标系中,曲线的参数方程为(为参数).在以坐标原点为极点,轴正半轴为极轴的极坐标系中,曲线,其中.
(1)说明是哪种曲线,并将方程化为极坐标方程;
(2)设曲线和曲线交于两点,求.
19. 已知函数 .
(1)若是的一个极值点,求值及的单调区间;
(2)当时,求在区间上的最值.
20. “生命重于泰山,疫情就是命令,防控就是责任”.面对疫情,为切实做好防控,落实“停课不停学”,某校高三年级启动线上公益学习活动,助“战”高考.为了解学生学习效果,李华老师在任教的甲、乙两个班中各随机抽取20名学生进行一次检测,根据他们取得的成绩(单位:分,满分100分)绘制了如下茎叶图,记成绩不低于70分者为“成绩优良”.
(1)分别估计甲、乙两个班“成绩优良”的概率;
(2)根据茎叶图判断哪个班的学习效果更好?并从两个角度来说明理由.
21. 已知函数.
(1)若函数在区间上递增,求实数的取值范围;
(2)求证:.
请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题计分.
22. 已知平面直角坐标系xOy中,曲线参数方程为(其中为参数,),直线的参数方程为(为参数,为锐角);以坐标原点为极点,轴的非负半轴为极轴建立极坐标系,.
(1)求曲线的极坐标方程以及直线的普通方程;
(2)记直线与、轴的交点分别为,,点在曲线上,直线AP的倾斜角为,若,求的值.
23. 已知函数.
(1)若,解不等式;
(2)若,且的最小值为,求证:.
涪江高级中学校2022-2023学年高三上学期9月开学考试
数学试题(理)答案
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
【1题答案】
【答案】A
【2题答案】
【答案】C
【3题答案】
【答案】C
【4题答案】
【答案】B
【5题答案】
【答案】B
【6题答案】
【答案】B
【7题答案】
【答案】C
【8题答案】
【答案】C
【9题答案】
【答案】D
【10题答案】
【答案】B
【11题答案】
【答案】C
【12题答案】
【答案】B
二、填空题:本题共4小题,每小题5分,共20分.
【13题答案】
【答案】
【14题答案】
【答案】-7或-1
【15题答案】
【答案】
【16题答案】
【答案】①④
三、解答题:本题共70分.解答应写出文字说明、证明过程或演算步骤.
【17题答案】
【答案】
【18题答案】
【答案】(1)是以为圆心,5为半径的圆;;(2).
【19题答案】
【答案】(1),单调递增区间为,单调递减区间为;
(2).
【20题答案】
【答案】(1)甲班“成绩优良”概率为,乙班“成绩优良”的概率为
(2)乙班学习的效果更好,理由略
【21题答案】
【答案】(1).(2)证明略.
请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题计分.
【22题答案】
【答案】(1),,,
(2)
【23题答案】
【答案】(1);(2)证明略.
数学试题(理)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知是虚数单位,若复数满足:,则复数( )
A. B. C. D.
2. 已知,,且,则的最小值为( )
A. 2 B. 4 C. 6 D. 8
3. 在集合和中各取一个数字组成一个两位数,则这个两位数能被4整除的概率为( )
A. B. C. D.
4. 已知实数,,满足,,,则实数,,的大小关系为( )
A. B. C. D.
5. 在中,“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
6. 月形是一种特殊的平面图形,指有相同的底,且在底的同一侧的两个弓形所围成的图形.月形中的一种特殊的情形是镰刀形,即由半圆和弓形所围成的图形(如下图),若半圆的半径与弓形所在圆的半径之比为,现向半圆内随机取一点,则取到镰刀形中的一点的概率为( )
A. B. C. D.
7. 设是函数的导函数,的图像如图所示,则的图像最有可能的是( )
A. B.
C. D.
8. 已知,则的零点个数为( )
A. B. C. D.
9. 已知为双曲线的右焦点,过原点的直线与双曲线交于,两点,若且的周长为,则该双曲线的离心率为( )
A. B. C. D.
10 已知抛物线焦点为,点为其准线与 轴的交点,过点的直线 与C相交于两点,则△ABD的面积的取值范围为( )
A. B.
C. D.
11. 已知对,不等式恒成立,则实数的最大值是( )
A. B. 1
C. D.
12. 椭圆有一条光学性质:从椭圆一个焦点出发的光线,经过椭圆反射后,一定经过另一个焦点.假设光线沿直线传播且在传播过程中不会衰减,椭圆的方程为,则光线从椭圆一个焦点出发,到首次回到该焦点所经过的路程不可能为( )
A. 2 B. 4 C. 6 D. 8
二、填空题:本题共4小题,每小题5分,共20分.
13. 曲线在点处的切线方程为__________.
14. 已知圆:与直线:相交于、两点,且,则实数______.
15. 若函数为定义在上的奇函数,当时,,则不等式的解集为______.
16. 已知x,,满足,给出下列四个结论:①;②;③;④.其中一定成立的结论是______(写出所有成立结论的编号).
三、解答题:本题共70分.解答应写出文字说明、证明过程或演算步骤.
17. 设命题:函数在区间上单调递减;命题:对恒成立.如果命题“且”为假命题,求的取值范围.
18. 在直角坐标系中,曲线的参数方程为(为参数).在以坐标原点为极点,轴正半轴为极轴的极坐标系中,曲线,其中.
(1)说明是哪种曲线,并将方程化为极坐标方程;
(2)设曲线和曲线交于两点,求.
19. 已知函数 .
(1)若是的一个极值点,求值及的单调区间;
(2)当时,求在区间上的最值.
20. “生命重于泰山,疫情就是命令,防控就是责任”.面对疫情,为切实做好防控,落实“停课不停学”,某校高三年级启动线上公益学习活动,助“战”高考.为了解学生学习效果,李华老师在任教的甲、乙两个班中各随机抽取20名学生进行一次检测,根据他们取得的成绩(单位:分,满分100分)绘制了如下茎叶图,记成绩不低于70分者为“成绩优良”.
(1)分别估计甲、乙两个班“成绩优良”的概率;
(2)根据茎叶图判断哪个班的学习效果更好?并从两个角度来说明理由.
21. 已知函数.
(1)若函数在区间上递增,求实数的取值范围;
(2)求证:.
请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题计分.
22. 已知平面直角坐标系xOy中,曲线参数方程为(其中为参数,),直线的参数方程为(为参数,为锐角);以坐标原点为极点,轴的非负半轴为极轴建立极坐标系,.
(1)求曲线的极坐标方程以及直线的普通方程;
(2)记直线与、轴的交点分别为,,点在曲线上,直线AP的倾斜角为,若,求的值.
23. 已知函数.
(1)若,解不等式;
(2)若,且的最小值为,求证:.
涪江高级中学校2022-2023学年高三上学期9月开学考试
数学试题(理)答案
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
【1题答案】
【答案】A
【2题答案】
【答案】C
【3题答案】
【答案】C
【4题答案】
【答案】B
【5题答案】
【答案】B
【6题答案】
【答案】B
【7题答案】
【答案】C
【8题答案】
【答案】C
【9题答案】
【答案】D
【10题答案】
【答案】B
【11题答案】
【答案】C
【12题答案】
【答案】B
二、填空题:本题共4小题,每小题5分,共20分.
【13题答案】
【答案】
【14题答案】
【答案】-7或-1
【15题答案】
【答案】
【16题答案】
【答案】①④
三、解答题:本题共70分.解答应写出文字说明、证明过程或演算步骤.
【17题答案】
【答案】
【18题答案】
【答案】(1)是以为圆心,5为半径的圆;;(2).
【19题答案】
【答案】(1),单调递增区间为,单调递减区间为;
(2).
【20题答案】
【答案】(1)甲班“成绩优良”概率为,乙班“成绩优良”的概率为
(2)乙班学习的效果更好,理由略
【21题答案】
【答案】(1).(2)证明略.
请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题计分.
【22题答案】
【答案】(1),,,
(2)
【23题答案】
【答案】(1);(2)证明略.
同课章节目录
