24.1 圆学案(共5课时)
文档属性
| 名称 | 24.1 圆学案(共5课时) |  | |
| 格式 | zip | ||
| 文件大小 | 267.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-15 20:04:51 | ||
图片预览


文档简介
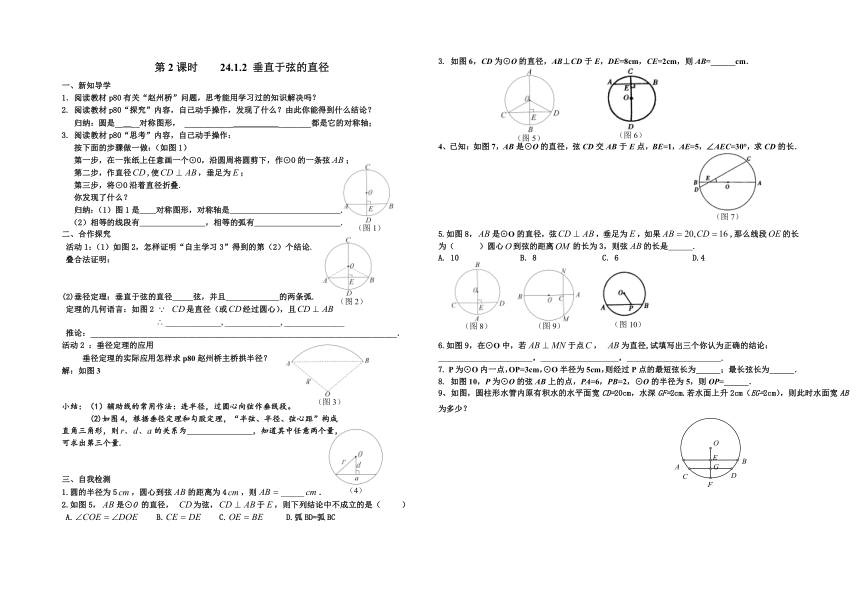
第1课时 24.1.1 圆
一、新知导学
1.圆的定义:把线段op的一个端点O ,使线段OP绕着点O在 旋转 ,
另一端点P运动所形成的图形叫做圆,其中点O叫做 ,线段OP叫做 .以O为圆心
的圆记作 .
2.圆的集合定义:圆是到 的点的集合.
3、从圆的定义中归纳:①圆上各点到定点(圆心)的距离都等于____ __;
②到定点的距离等于定长的点都在____ _.
4、圆的表示方法:以点为圆心的圆记作______,读作______.
5、要确定一个圆,需要两个基本条件,一个是______,另一个是_____,其中_____确定圆的位置,______确定圆的大小.
6;如图1,弦有线段 ,直径是 ,
最长的弦是 ,优弧有 ;劣弧有 。
二、合作探究
1.判断下列说法是否正确,为什么?
(1)直径是弦.( ) (2)弦是直径.( )
(3)半圆是弧.( ) (4) 弧是半圆.( )
(5) 等弧的长度相等.( ) (6) 长度相等的两条弧是等弧.( )
2.⊙O的半径为2㎝,弦AB所对的劣弧为圆周长的,则∠AOB= ,AB=
3.已知:如图2,为的半径,分别为的中点,
求证:(1) (2)
4.对角线互相垂直的四边形的各边的中点是否在同一个圆上?并说明理由.
三、自我检测
1.到定点O的距离为2cm的点的集合是以 为圆心, 为半径的圆.
2.正方形的四个顶点在以 为圆心,以 为半径的圆上.
3.一个点与定圆最近点的距离为4cm, 与最远点的距离是9cm,则圆的半径是
4.下列说法正确的有( )
①半径相等的两个圆是等圆; ②半径相等的两个半圆是等弧;
③过圆心的线段是直径; ④ 分别在两个等圆上的两条弧是等弧.
A. 1个 B. 2个 C. 3个 D. 4个
5.如图3,点以及点分别在一条直线上,则圆中有 条弦.
6、下列说法正确的是 (填序号)
①直径是弦 ②弦是直径 ③半径是弦 ④半圆是弧,但弧不一定是半圆
⑤半径相等的两个半圆是等弧 ⑥长度相等的两条弧是等弧 ⑦等弧的长度相等
7.圆O的半径为3 ,则圆O中最长的弦长为
8.如图4,在中,以为圆心,为半径的圆交于点,求的度数.
9、已知:如图5,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠E=18°,求∠C及∠AOC的度数.
第2课时 24.1.2 垂直于弦的直径
一、新知导学
1.阅读教材p80有关“赵州桥”问题,思考能用学习过的知识解决吗?
2. 阅读教材p80“探究”内容,自己动手操作,发现了什么?由此你能得到什么结论?
归纳:圆是__ __对称图形, ____________ ________都是它的对称轴;
3. 阅读教材p80“思考”内容,自己动手操作:
按下面的步骤做一做:(如图1)
第一步,在一张纸上任意画一个⊙O,沿圆周将圆剪下,作⊙O的一条弦;
第二步,作直径,使,垂足为;
第三步,将⊙O沿着直径折叠.
你发现了什么?
归纳:(1)图1是 对称图形,对称轴是 .
(2)相等的线段有 ,相等的弧有 .
二、合作探究
活动1:(1)如图2,怎样证明“自主学习3”得到的第(2)个结论.
叠合法证明:
(2)垂径定理:垂直于弦的直径 弦,并且 的两条弧.
定理的几何语言:如图2 是直径(或经过圆心),且
推论:___________________________________________________________________________.
活动2 :垂径定理的应用
垂径定理的实际应用怎样求p80赵州桥主桥拱半径?
解:如图3
小结:(1)辅助线的常用作法:连半径,过圆心向弦作垂线段。
(2)如图4,根据垂径定理和勾股定理,“半弦、半径、弦心距”构成
直角三角形,则的关系为 ,知道其中任意两个量,
可求出第三个量.
三、自我检测
1.圆的半径为5,圆心到弦的距离为4,则.
2.如图5,是⊙O 的直径, 为弦,于,则下列结论中不成立的是( )
A. B. C. D.弧BD=弧BC
3. 如图6,CD为⊙O的直径,AB⊥CD于E,DE=8cm,CE=2cm,则AB=______cm.
4、已知:如图7,AB是⊙O的直径,弦CD交AB于E点,BE=1,AE=5,∠AEC=30°,求CD的长.
5.如图8,是⊙O的直径,弦,垂足为,如果,那么线段的长为( )圆心到弦的距离的长为3,则弦的长是 .
A. 10 B. 8 C. 6 D.4
6.如图9,在⊙O中,若于点, 为直径,试填写出三个你认为正确的结论:
, , .
7. P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最短弦长为______;最长弦长为______.
8. 如图10,P为⊙O的弦AB上的点,PA=6,PB=2,⊙O的半径为5,则OP=______.
9、如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm.若水面上升2cm(EG=2cm),则此时水面宽AB为多少?
第3课时 24.1.3 弧、弦、圆心角
教学目标:
结合图形了解圆心角的概念,学会辨别圆心角。
2.发现圆心角、弦、弧之间的相等关系,并初步学会运用这些关系解决有关问题。
教学过程:
一.预习检测:
如图所示,∠AOB的顶点在圆心,像这样 的角叫做圆心角.
二.合作探究:
1、如图所示的⊙O中,将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置,你能发现哪些等量关系?为什么?
因此,在同一个圆中,相等的圆心角所对的_____相等,所对的 相等.
2、 在⊙O和⊙O′中,分别作相等的圆心角∠AOB和
∠A′O′B′得到如图2,滚动一个圆,使O与O′重合,
固定圆心,将其中的一个圆旋转一个角度,使得OA与
O′A′重合.
在等圆中,相等的圆心角是否也有所对的弧相等,所对的弦相等吗?
因此,我们可以得到下面的定理:____________________________________________
_____________________________________。
同样,还可以得到:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角___ _,所对的弦也__ _
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角__ __,所对的弧也__ _
探究:1、课本P83,例1.
2、 如图,在⊙O中,AB、CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为EF.
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
(2)如果OE=OF,那么弧AB与弧CD的大小有什么关系?AB与CD的大小有什么关系?为什么?∠AOB与∠COD呢?
三. 达标测评
1.如果两个圆心角相等,那么( )
A.这两个圆心角所对的弦相等;B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等;D.以上说法都不对
2.在同圆中,圆心角∠AOB=2∠COD,则两条弧AB与CD关系是( )
A.=2 B.> C.<2 D.不能确定 .
3.一条弦长恰好为半径长,则此弦所对的弧是半圆的_________.
4.如图4,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE=________.
5.如图,⊙中,如果=2,那么( ).
A. B. C. D.
图4 5题图
6. 已知:如图,点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点A、B 和C、D。求证:∠OBA=∠OCD。
7、已知:O是∠EPF的平分线上所在直线上一点,以O为圆心的圆和∠EPF的两边所在直线分别交于A、B和C、D(1)求证:AB=CD;(2)当P点在⊙O上时,上述结论成立吗?为什么?(3)当P点在⊙O内时,上述结论成立吗?为什么?
四、课外作业:
一、填空题
1.如图,AB、CE是⊙O的直径,∠COD=60°,且弧AD=弧BC,那么与∠AOE相等的角有_____,
与∠AOC相等的角有_________.
2.一条弦把圆分成1:3两部分,则弦所对的圆心角为________.
3.弦心距是弦的一半时,弦与直径的比是________,弦所对的圆心角是_____.
4.如图,AB为圆O的直径,弧BD=弧BC,∠A=25°,则∠BOD=______.
5.如图,AB、CD是⊙O的两条弦,M、N分别为AB、CD的中点,且∠AMN=∠CNM,AB=6,则CD=_______.
6.如图,直角坐标系中一条圆弧经过网格点A、B、C,其中B点坐标为(4,4),则该圆弧所
在圆的圆心坐标为_________.
7.如图所示,已知C为弧AB的中点,OA⊥CD于M,CN⊥OB于N,若OA=r,ON=a,则CD=_______.
二、选择题
8.如果两条弦相等,那么( )
A.这两条弦所对的弧相等 B.这两条弦所对的圆心角相等
C.这两条弦的弦心距相等 D.以上答案都不对
9.如图4,在圆O中,直径MN⊥AB,垂足为C,则下列结论中错误的是( )
A.AC=BC B.弧AN=弧BN C.弧AM=弧BM D.OC=CN
10.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的直径的长为( )
A.4 B.8 C.24 D.16
11.如图5,在半径为2cm的圆O内有长为2cm的弦AB,则此弦所对的圆心角∠AOB为()
A.60° B.90° C.120° D.150°
12.如图6,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不一定成立的是( )
A.∠COE=∠DOE B.CE=DE C.OE=BE D.弧BD=弧BC
13.如图7所示,在△ABC中,∠A=70°,⊙O截△ABC的三边所得的弦长相等,则∠BOC=( )
A.140° B.135° C.130° D.125°
图
三、解答题:
14.如图,在⊙O中,AB、CD是弦,点E、F是AB、CD的中点,并且=,
(1)求证:∠AEF=∠CFE;(2)若∠EOF=120°,OE=4cm,求:EF的长.
15.如图7-44,AB是⊙O的直径,弦CD和AB相交于P,且∠APC=45°,OQ是弦CD的弦心距,(1)求证:PC-PD=2OQ;(2)若⊙O的半径为5cm,求的值.
第4课时 圆周角(1)
新知导学
圆周角的定义
顶点在 ,并且两边都和圆 的角叫做圆周角.
2.圆周角定理
在同圆或等圆中,同弧或等弧所对的圆周角 ,都等于该弧所对的圆心角的 .
二、合作探究
1.如图,⊙O的直径AB=8cm,∠CBD=30°,求弦DC的长.
2.如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC= ∠CAD,求弦AC的长.
【自我检测】
一、选择题:
1.在半径为R的圆中有一条长度为R的弦,则该弦所对的圆周角的度数是( )
A.30° B.30°或150° C.60° D.60°或120°
2.如图,A、B、C三点都在⊙O上,点D是AB延长线上一点,∠AOC=140°, ∠CBD 的度数是( )
A.40° B.50° C.70° D.110°
3.如图1,已知圆心角∠BOC=100°,则圆周角∠BAC的度数是( )
A.50° B.100° C.130° D.200°
4.如图2,A、B、C、D四点在同一个圆上,四边形ABCD 的对角线把四个内角分成的八个角中,相等的角有( ) A.2对 B.3对 C.4对 D.5对
5.如图3,D是弧AC的中点,则图中与∠ABD相等的角的个数是( )A.4个 B.3个C.2个 D.1个
6.如图4,∠AOB=100°,则∠A+∠B等于( )
A.100° B.80° C.50° D.40°
7.如图⊙O中弧AB的度数为60°,AC是⊙O的直径,那么∠BOC等于 ( )
A.150° B.130° C.120° D.60°
二、填空题:
8.如图,等边三角形ABC的三个顶点都在⊙O上,D是弧AC上任一点(不与A、C重合),
则∠ADC的度数是________.
9.如图,四边形ABCD的四个顶点都在⊙O上,且AD∥BC,对角线AC与BC相交于点E,那么图中
有_________对全等三角形;________对相似比不等于1的相似三角形.
10.已知,如图,∠BAC的对角∠BAD=100°,则∠BOC=_______度.
11.如图,A、B、C为⊙O上三点,若∠OAB=46°,则∠ACB=_______度.
12.如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=______.
三、解答题:
13.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是弧CAD上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.
(2)点P′在劣弧CD上(不与C、D重合时),∠CP′D与∠COB有什么数量关系 请证明你的结论.
14.在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻.当甲带球部到A点时,乙随后冲到B点,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢 为什么 (不考虑其他因素)
第5课时 圆周角(2)
一、新知导学
1.直径(或半圆)所对的圆周角是 .
2.900的圆周角所对的弦是 .
二、合作探究
1.如图,AB是半圆的直径,AC为弦,OD⊥AB,交AC于点D,垂足为O,⊙O的半径为4,
OD=3,求CD的长.
2.如图,AB是⊙O的直径,AB=AC,D、E在⊙O上.求证:BD=DE.
三、自我检测
一、填空题
1.如图,AB是⊙O的直径,∠AOD是圆心角,∠BCD是圆周角.若∠BCD=25°,则∠AOD= .
2.如图,⊙O直径MN⊥AB于P,∠BMN=30°,则∠AON= .
3.如图,A、B、C是⊙O上三点,∠BAC的平分线AM交BC于点D,交⊙O于点M.若∠BAC=60°,∠ABC=50°,则∠CBM= ,∠AMB= .
4.⊙O中,若弦AB长2cm,弦心距为cm,则此弦所对的圆周角等于 .
5.如图,⊙O中,两条弦AB⊥BC,AB=6,BC=8,求⊙O的半径= .
二、选择题
6.下列说法正确的是( )
A.顶点在圆上的角是圆周角 B.两边都和圆相交的角是圆周角
C.圆心角是圆周角的2倍 D.圆周角度数等于它所对圆心角度数的一半
7.下列说法错误的是( )
A.等弧所对圆周角相等 B.同弧所对圆周角相等
C.同圆中,相等的圆周角所对弧也相等. D.同圆中,等弦所对的圆周角相等
8.在⊙O中,同弦所对的圆周角( )
A.相等 B.互补 C.相等或互补 D.都不对
9.如图,在⊙O中,弦AD=弦DC,则图中相等的圆周角的对数是( )
A.5对 B.6对 C.7对 D.8对
三、解答及证明题
10.如图,AB是⊙O的直径,FB交⊙O于点G,FD⊥AB,垂足为D,
FD交AG于E.求证:EF·DE=AE·EG.
11.如图,△ABC内接于⊙O,E为的中点.求证:AB·BE=AE·BD.
12.根据图中所给的条件,求△AOB的面积及圆的面积.
13.如图,在圆内接△ABC中,AB=AC,D是BC边上一点.
(1)求证:AB2=AD·AE;
(2)当D为BC延长线上一点时,第(1)小题的结论还成立吗?如果成立,请证明;
如果不成立,请说明理由.
14.如图,以△ABC的BC边为直径的半圆交AB于D,交AC于E,过E点作
EF⊥BC,垂足为F,且BF:FC=5:1,AB=8,AE=2,
求EC的长.
(图1)
(图2)
(图4)
(图3)
(图5)
(图1)
(图2)
(图3)
(4)
(图6)
(图5)
(图7)
(图9)
(图8)
(图10)
(2)
一、新知导学
1.圆的定义:把线段op的一个端点O ,使线段OP绕着点O在 旋转 ,
另一端点P运动所形成的图形叫做圆,其中点O叫做 ,线段OP叫做 .以O为圆心
的圆记作 .
2.圆的集合定义:圆是到 的点的集合.
3、从圆的定义中归纳:①圆上各点到定点(圆心)的距离都等于____ __;
②到定点的距离等于定长的点都在____ _.
4、圆的表示方法:以点为圆心的圆记作______,读作______.
5、要确定一个圆,需要两个基本条件,一个是______,另一个是_____,其中_____确定圆的位置,______确定圆的大小.
6;如图1,弦有线段 ,直径是 ,
最长的弦是 ,优弧有 ;劣弧有 。
二、合作探究
1.判断下列说法是否正确,为什么?
(1)直径是弦.( ) (2)弦是直径.( )
(3)半圆是弧.( ) (4) 弧是半圆.( )
(5) 等弧的长度相等.( ) (6) 长度相等的两条弧是等弧.( )
2.⊙O的半径为2㎝,弦AB所对的劣弧为圆周长的,则∠AOB= ,AB=
3.已知:如图2,为的半径,分别为的中点,
求证:(1) (2)
4.对角线互相垂直的四边形的各边的中点是否在同一个圆上?并说明理由.
三、自我检测
1.到定点O的距离为2cm的点的集合是以 为圆心, 为半径的圆.
2.正方形的四个顶点在以 为圆心,以 为半径的圆上.
3.一个点与定圆最近点的距离为4cm, 与最远点的距离是9cm,则圆的半径是
4.下列说法正确的有( )
①半径相等的两个圆是等圆; ②半径相等的两个半圆是等弧;
③过圆心的线段是直径; ④ 分别在两个等圆上的两条弧是等弧.
A. 1个 B. 2个 C. 3个 D. 4个
5.如图3,点以及点分别在一条直线上,则圆中有 条弦.
6、下列说法正确的是 (填序号)
①直径是弦 ②弦是直径 ③半径是弦 ④半圆是弧,但弧不一定是半圆
⑤半径相等的两个半圆是等弧 ⑥长度相等的两条弧是等弧 ⑦等弧的长度相等
7.圆O的半径为3 ,则圆O中最长的弦长为
8.如图4,在中,以为圆心,为半径的圆交于点,求的度数.
9、已知:如图5,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠E=18°,求∠C及∠AOC的度数.
第2课时 24.1.2 垂直于弦的直径
一、新知导学
1.阅读教材p80有关“赵州桥”问题,思考能用学习过的知识解决吗?
2. 阅读教材p80“探究”内容,自己动手操作,发现了什么?由此你能得到什么结论?
归纳:圆是__ __对称图形, ____________ ________都是它的对称轴;
3. 阅读教材p80“思考”内容,自己动手操作:
按下面的步骤做一做:(如图1)
第一步,在一张纸上任意画一个⊙O,沿圆周将圆剪下,作⊙O的一条弦;
第二步,作直径,使,垂足为;
第三步,将⊙O沿着直径折叠.
你发现了什么?
归纳:(1)图1是 对称图形,对称轴是 .
(2)相等的线段有 ,相等的弧有 .
二、合作探究
活动1:(1)如图2,怎样证明“自主学习3”得到的第(2)个结论.
叠合法证明:
(2)垂径定理:垂直于弦的直径 弦,并且 的两条弧.
定理的几何语言:如图2 是直径(或经过圆心),且
推论:___________________________________________________________________________.
活动2 :垂径定理的应用
垂径定理的实际应用怎样求p80赵州桥主桥拱半径?
解:如图3
小结:(1)辅助线的常用作法:连半径,过圆心向弦作垂线段。
(2)如图4,根据垂径定理和勾股定理,“半弦、半径、弦心距”构成
直角三角形,则的关系为 ,知道其中任意两个量,
可求出第三个量.
三、自我检测
1.圆的半径为5,圆心到弦的距离为4,则.
2.如图5,是⊙O 的直径, 为弦,于,则下列结论中不成立的是( )
A. B. C. D.弧BD=弧BC
3. 如图6,CD为⊙O的直径,AB⊥CD于E,DE=8cm,CE=2cm,则AB=______cm.
4、已知:如图7,AB是⊙O的直径,弦CD交AB于E点,BE=1,AE=5,∠AEC=30°,求CD的长.
5.如图8,是⊙O的直径,弦,垂足为,如果,那么线段的长为( )圆心到弦的距离的长为3,则弦的长是 .
A. 10 B. 8 C. 6 D.4
6.如图9,在⊙O中,若于点, 为直径,试填写出三个你认为正确的结论:
, , .
7. P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最短弦长为______;最长弦长为______.
8. 如图10,P为⊙O的弦AB上的点,PA=6,PB=2,⊙O的半径为5,则OP=______.
9、如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm.若水面上升2cm(EG=2cm),则此时水面宽AB为多少?
第3课时 24.1.3 弧、弦、圆心角
教学目标:
结合图形了解圆心角的概念,学会辨别圆心角。
2.发现圆心角、弦、弧之间的相等关系,并初步学会运用这些关系解决有关问题。
教学过程:
一.预习检测:
如图所示,∠AOB的顶点在圆心,像这样 的角叫做圆心角.
二.合作探究:
1、如图所示的⊙O中,将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置,你能发现哪些等量关系?为什么?
因此,在同一个圆中,相等的圆心角所对的_____相等,所对的 相等.
2、 在⊙O和⊙O′中,分别作相等的圆心角∠AOB和
∠A′O′B′得到如图2,滚动一个圆,使O与O′重合,
固定圆心,将其中的一个圆旋转一个角度,使得OA与
O′A′重合.
在等圆中,相等的圆心角是否也有所对的弧相等,所对的弦相等吗?
因此,我们可以得到下面的定理:____________________________________________
_____________________________________。
同样,还可以得到:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角___ _,所对的弦也__ _
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角__ __,所对的弧也__ _
探究:1、课本P83,例1.
2、 如图,在⊙O中,AB、CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为EF.
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
(2)如果OE=OF,那么弧AB与弧CD的大小有什么关系?AB与CD的大小有什么关系?为什么?∠AOB与∠COD呢?
三. 达标测评
1.如果两个圆心角相等,那么( )
A.这两个圆心角所对的弦相等;B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等;D.以上说法都不对
2.在同圆中,圆心角∠AOB=2∠COD,则两条弧AB与CD关系是( )
A.=2 B.> C.<2 D.不能确定 .
3.一条弦长恰好为半径长,则此弦所对的弧是半圆的_________.
4.如图4,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE=________.
5.如图,⊙中,如果=2,那么( ).
A. B. C. D.
图4 5题图
6. 已知:如图,点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点A、B 和C、D。求证:∠OBA=∠OCD。
7、已知:O是∠EPF的平分线上所在直线上一点,以O为圆心的圆和∠EPF的两边所在直线分别交于A、B和C、D(1)求证:AB=CD;(2)当P点在⊙O上时,上述结论成立吗?为什么?(3)当P点在⊙O内时,上述结论成立吗?为什么?
四、课外作业:
一、填空题
1.如图,AB、CE是⊙O的直径,∠COD=60°,且弧AD=弧BC,那么与∠AOE相等的角有_____,
与∠AOC相等的角有_________.
2.一条弦把圆分成1:3两部分,则弦所对的圆心角为________.
3.弦心距是弦的一半时,弦与直径的比是________,弦所对的圆心角是_____.
4.如图,AB为圆O的直径,弧BD=弧BC,∠A=25°,则∠BOD=______.
5.如图,AB、CD是⊙O的两条弦,M、N分别为AB、CD的中点,且∠AMN=∠CNM,AB=6,则CD=_______.
6.如图,直角坐标系中一条圆弧经过网格点A、B、C,其中B点坐标为(4,4),则该圆弧所
在圆的圆心坐标为_________.
7.如图所示,已知C为弧AB的中点,OA⊥CD于M,CN⊥OB于N,若OA=r,ON=a,则CD=_______.
二、选择题
8.如果两条弦相等,那么( )
A.这两条弦所对的弧相等 B.这两条弦所对的圆心角相等
C.这两条弦的弦心距相等 D.以上答案都不对
9.如图4,在圆O中,直径MN⊥AB,垂足为C,则下列结论中错误的是( )
A.AC=BC B.弧AN=弧BN C.弧AM=弧BM D.OC=CN
10.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的直径的长为( )
A.4 B.8 C.24 D.16
11.如图5,在半径为2cm的圆O内有长为2cm的弦AB,则此弦所对的圆心角∠AOB为()
A.60° B.90° C.120° D.150°
12.如图6,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不一定成立的是( )
A.∠COE=∠DOE B.CE=DE C.OE=BE D.弧BD=弧BC
13.如图7所示,在△ABC中,∠A=70°,⊙O截△ABC的三边所得的弦长相等,则∠BOC=( )
A.140° B.135° C.130° D.125°
图
三、解答题:
14.如图,在⊙O中,AB、CD是弦,点E、F是AB、CD的中点,并且=,
(1)求证:∠AEF=∠CFE;(2)若∠EOF=120°,OE=4cm,求:EF的长.
15.如图7-44,AB是⊙O的直径,弦CD和AB相交于P,且∠APC=45°,OQ是弦CD的弦心距,(1)求证:PC-PD=2OQ;(2)若⊙O的半径为5cm,求的值.
第4课时 圆周角(1)
新知导学
圆周角的定义
顶点在 ,并且两边都和圆 的角叫做圆周角.
2.圆周角定理
在同圆或等圆中,同弧或等弧所对的圆周角 ,都等于该弧所对的圆心角的 .
二、合作探究
1.如图,⊙O的直径AB=8cm,∠CBD=30°,求弦DC的长.
2.如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC= ∠CAD,求弦AC的长.
【自我检测】
一、选择题:
1.在半径为R的圆中有一条长度为R的弦,则该弦所对的圆周角的度数是( )
A.30° B.30°或150° C.60° D.60°或120°
2.如图,A、B、C三点都在⊙O上,点D是AB延长线上一点,∠AOC=140°, ∠CBD 的度数是( )
A.40° B.50° C.70° D.110°
3.如图1,已知圆心角∠BOC=100°,则圆周角∠BAC的度数是( )
A.50° B.100° C.130° D.200°
4.如图2,A、B、C、D四点在同一个圆上,四边形ABCD 的对角线把四个内角分成的八个角中,相等的角有( ) A.2对 B.3对 C.4对 D.5对
5.如图3,D是弧AC的中点,则图中与∠ABD相等的角的个数是( )A.4个 B.3个C.2个 D.1个
6.如图4,∠AOB=100°,则∠A+∠B等于( )
A.100° B.80° C.50° D.40°
7.如图⊙O中弧AB的度数为60°,AC是⊙O的直径,那么∠BOC等于 ( )
A.150° B.130° C.120° D.60°
二、填空题:
8.如图,等边三角形ABC的三个顶点都在⊙O上,D是弧AC上任一点(不与A、C重合),
则∠ADC的度数是________.
9.如图,四边形ABCD的四个顶点都在⊙O上,且AD∥BC,对角线AC与BC相交于点E,那么图中
有_________对全等三角形;________对相似比不等于1的相似三角形.
10.已知,如图,∠BAC的对角∠BAD=100°,则∠BOC=_______度.
11.如图,A、B、C为⊙O上三点,若∠OAB=46°,则∠ACB=_______度.
12.如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=______.
三、解答题:
13.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是弧CAD上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.
(2)点P′在劣弧CD上(不与C、D重合时),∠CP′D与∠COB有什么数量关系 请证明你的结论.
14.在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻.当甲带球部到A点时,乙随后冲到B点,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢 为什么 (不考虑其他因素)
第5课时 圆周角(2)
一、新知导学
1.直径(或半圆)所对的圆周角是 .
2.900的圆周角所对的弦是 .
二、合作探究
1.如图,AB是半圆的直径,AC为弦,OD⊥AB,交AC于点D,垂足为O,⊙O的半径为4,
OD=3,求CD的长.
2.如图,AB是⊙O的直径,AB=AC,D、E在⊙O上.求证:BD=DE.
三、自我检测
一、填空题
1.如图,AB是⊙O的直径,∠AOD是圆心角,∠BCD是圆周角.若∠BCD=25°,则∠AOD= .
2.如图,⊙O直径MN⊥AB于P,∠BMN=30°,则∠AON= .
3.如图,A、B、C是⊙O上三点,∠BAC的平分线AM交BC于点D,交⊙O于点M.若∠BAC=60°,∠ABC=50°,则∠CBM= ,∠AMB= .
4.⊙O中,若弦AB长2cm,弦心距为cm,则此弦所对的圆周角等于 .
5.如图,⊙O中,两条弦AB⊥BC,AB=6,BC=8,求⊙O的半径= .
二、选择题
6.下列说法正确的是( )
A.顶点在圆上的角是圆周角 B.两边都和圆相交的角是圆周角
C.圆心角是圆周角的2倍 D.圆周角度数等于它所对圆心角度数的一半
7.下列说法错误的是( )
A.等弧所对圆周角相等 B.同弧所对圆周角相等
C.同圆中,相等的圆周角所对弧也相等. D.同圆中,等弦所对的圆周角相等
8.在⊙O中,同弦所对的圆周角( )
A.相等 B.互补 C.相等或互补 D.都不对
9.如图,在⊙O中,弦AD=弦DC,则图中相等的圆周角的对数是( )
A.5对 B.6对 C.7对 D.8对
三、解答及证明题
10.如图,AB是⊙O的直径,FB交⊙O于点G,FD⊥AB,垂足为D,
FD交AG于E.求证:EF·DE=AE·EG.
11.如图,△ABC内接于⊙O,E为的中点.求证:AB·BE=AE·BD.
12.根据图中所给的条件,求△AOB的面积及圆的面积.
13.如图,在圆内接△ABC中,AB=AC,D是BC边上一点.
(1)求证:AB2=AD·AE;
(2)当D为BC延长线上一点时,第(1)小题的结论还成立吗?如果成立,请证明;
如果不成立,请说明理由.
14.如图,以△ABC的BC边为直径的半圆交AB于D,交AC于E,过E点作
EF⊥BC,垂足为F,且BF:FC=5:1,AB=8,AE=2,
求EC的长.
(图1)
(图2)
(图4)
(图3)
(图5)
(图1)
(图2)
(图3)
(4)
(图6)
(图5)
(图7)
(图9)
(图8)
(图10)
(2)
同课章节目录
