2022-2023学年人教版九年级数学上册22.1.4二次函数y=ax2+bx+c的图象和性质(第1课时)课件(共15张PPT)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册22.1.4二次函数y=ax2+bx+c的图象和性质(第1课时)课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-16 08:32:59 | ||
图片预览





文档简介
(共15张PPT)
22.1.4 二次函数 y=ax2+bx+c 的图象和性质
温故知新
y=ax2+k
y=a(x-h)2
y=a(x-h)2+k
y=ax2
类比
从特殊到一般
转化
上(下)平移
上(下)平移
左(右)平移
上(下)平移
左(右)平移
左(右)平移
数形结合
1.你研究过哪些形式的二次函数的图象和性质?是怎样研究的?
图象 开口方向 顶点坐标 对称轴 最值
(0,0)
y轴(直线x=0)
0
(0,3)
直线x=0
3
(6,0)
直线x=6
0
(6,3)
直线x=6
3
向上
向上
向上
向上
2.填一填:
问题:
当一枚火箭被竖直向上发射时,它的高度 h (m) 与时间 t (s) 的关系可以用公式 h = - 5 t + 150 t +10 表示,经过多长时间,火箭到达它的最高点?最高点的高度是多少?
今天我们继续学习:
二次函数的一般形式y=ax2+bx+c(a≠0)的图象和性质
同学们想知道如何求这道题吗?
配方得:
y= x2-6x+21
=
(x-6)2+3
由此可知,抛物线
的顶点是点(6,3),对称轴是直线 x=6.
y= x2-6x+21
我们已经知道, 这样的函数图像和性质,能否利用这些知识来讨论二次函数 的图像和性质 ?
探究一
三、新课
(具体书写板演过程)
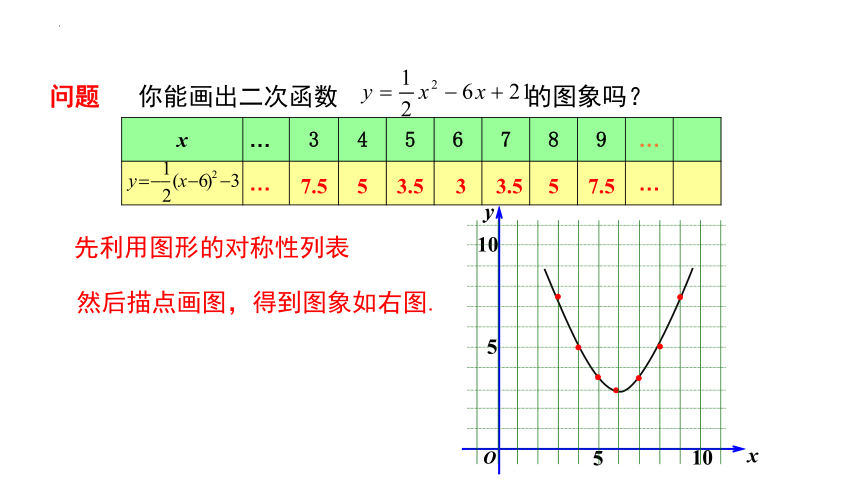
问题 你能画出二次函数 的图象吗?
…
…
…
…
9
8
7
6
5
4
3
x
先利用图形的对称性列表
7.5
5
3.5
3
3.5
5
7.5
5
10
x
y
5
10
然后描点画图,得到图象如右图.
O
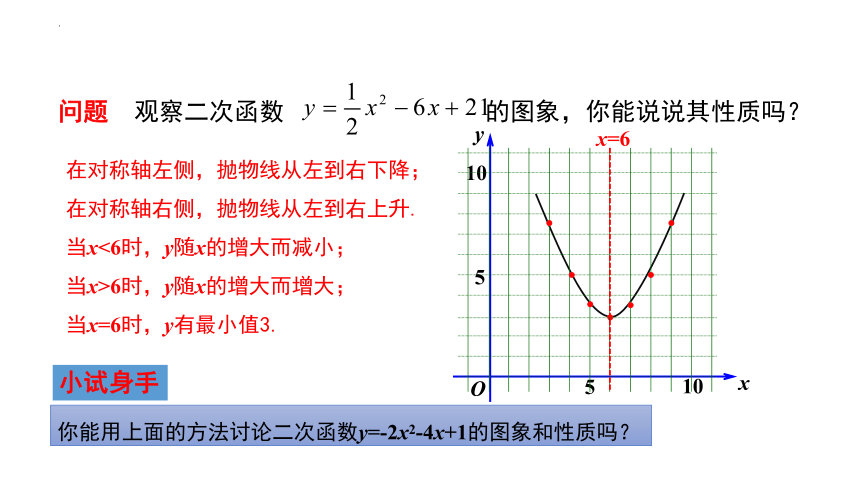
问题 观察二次函数 的图象,你能说说其性质吗?
5
10
x
y
5
10
x=6
在对称轴左侧,抛物线从左到右下降;
在对称轴右侧,抛物线从左到右上升.
当x<6时,y随x的增大而减小;
当x>6时,y随x的增大而增大;
当x=6时,y有最小值3.
O
你能用上面的方法讨论二次函数y=-2x2-4x+1的图象和性质吗?
小试身手
向下
(-1,3)
x=-1
3
大
-1
左(或上)
3(或1)
上(或左)
1(或3)
二次函数y=-2x2-4x+1的图象和性质
大于3
小于3
想一想
解:
我们也可以利用这个结论来求出二次函数的对称轴和顶点坐标.
1
方法一:配方法
方法二:公式法
设顶点式为 y= a(x-h) +k
C
2
D
3
知识小结
列表
图象的对称性
转化
描点法
y= ax +bx+c (a≠0) 图象 开口 顶点坐标 对称轴 增减性 最值
a>0
a<0
向上
向下
直线
在对称轴左侧
即当x< 时,
y 随 x的增大而减小.
在对称轴右侧
即当x> 时,
y随 x 的增大而增大.
在对称轴左侧
即当x< 时,
y 随 x的增大而增大,
在对称轴右侧
即当x> 时,
y随 x 的增大而减小.
当 时,
y最小值=
15
二次函数 y=ax +bx+c 的图形和性质
x
y
y
x
当 时,
y最大值=
4ac﹣b
4a
4ac﹣b
4a
22.1.4 二次函数 y=ax2+bx+c 的图象和性质
温故知新
y=ax2+k
y=a(x-h)2
y=a(x-h)2+k
y=ax2
类比
从特殊到一般
转化
上(下)平移
上(下)平移
左(右)平移
上(下)平移
左(右)平移
左(右)平移
数形结合
1.你研究过哪些形式的二次函数的图象和性质?是怎样研究的?
图象 开口方向 顶点坐标 对称轴 最值
(0,0)
y轴(直线x=0)
0
(0,3)
直线x=0
3
(6,0)
直线x=6
0
(6,3)
直线x=6
3
向上
向上
向上
向上
2.填一填:
问题:
当一枚火箭被竖直向上发射时,它的高度 h (m) 与时间 t (s) 的关系可以用公式 h = - 5 t + 150 t +10 表示,经过多长时间,火箭到达它的最高点?最高点的高度是多少?
今天我们继续学习:
二次函数的一般形式y=ax2+bx+c(a≠0)的图象和性质
同学们想知道如何求这道题吗?
配方得:
y= x2-6x+21
=
(x-6)2+3
由此可知,抛物线
的顶点是点(6,3),对称轴是直线 x=6.
y= x2-6x+21
我们已经知道, 这样的函数图像和性质,能否利用这些知识来讨论二次函数 的图像和性质 ?
探究一
三、新课
(具体书写板演过程)
问题 你能画出二次函数 的图象吗?
…
…
…
…
9
8
7
6
5
4
3
x
先利用图形的对称性列表
7.5
5
3.5
3
3.5
5
7.5
5
10
x
y
5
10
然后描点画图,得到图象如右图.
O
问题 观察二次函数 的图象,你能说说其性质吗?
5
10
x
y
5
10
x=6
在对称轴左侧,抛物线从左到右下降;
在对称轴右侧,抛物线从左到右上升.
当x<6时,y随x的增大而减小;
当x>6时,y随x的增大而增大;
当x=6时,y有最小值3.
O
你能用上面的方法讨论二次函数y=-2x2-4x+1的图象和性质吗?
小试身手
向下
(-1,3)
x=-1
3
大
-1
左(或上)
3(或1)
上(或左)
1(或3)
二次函数y=-2x2-4x+1的图象和性质
大于3
小于3
想一想
解:
我们也可以利用这个结论来求出二次函数的对称轴和顶点坐标.
1
方法一:配方法
方法二:公式法
设顶点式为 y= a(x-h) +k
C
2
D
3
知识小结
列表
图象的对称性
转化
描点法
y= ax +bx+c (a≠0) 图象 开口 顶点坐标 对称轴 增减性 最值
a>0
a<0
向上
向下
直线
在对称轴左侧
即当x< 时,
y 随 x的增大而减小.
在对称轴右侧
即当x> 时,
y随 x 的增大而增大.
在对称轴左侧
即当x< 时,
y 随 x的增大而增大,
在对称轴右侧
即当x> 时,
y随 x 的增大而减小.
当 时,
y最小值=
15
二次函数 y=ax +bx+c 的图形和性质
x
y
y
x
当 时,
y最大值=
4ac﹣b
4a
4ac﹣b
4a
同课章节目录
