2022年秋京改版数学九年级上册 19.3二次函数的性质 课件(共13张PPT)
文档属性
| 名称 | 2022年秋京改版数学九年级上册 19.3二次函数的性质 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 00:00:00 | ||
图片预览



文档简介
(共13张PPT)
19.3二次函数的性质
复习引入
观察函数y= x+1,y= -x+1 的图象,
函数有最大(小)值吗?y随自变量x
的增大怎样变化?
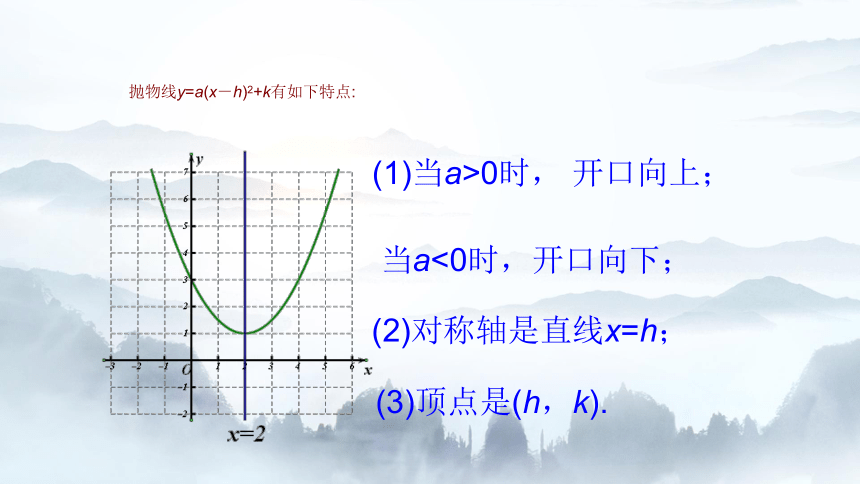
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时, 开口向上;
当a<0时,开口向下;
(2)对称轴是直线x=h;
(3)顶点是(h,k).
函数有最大(小)值吗?
y随自变量x的增大怎样变化?
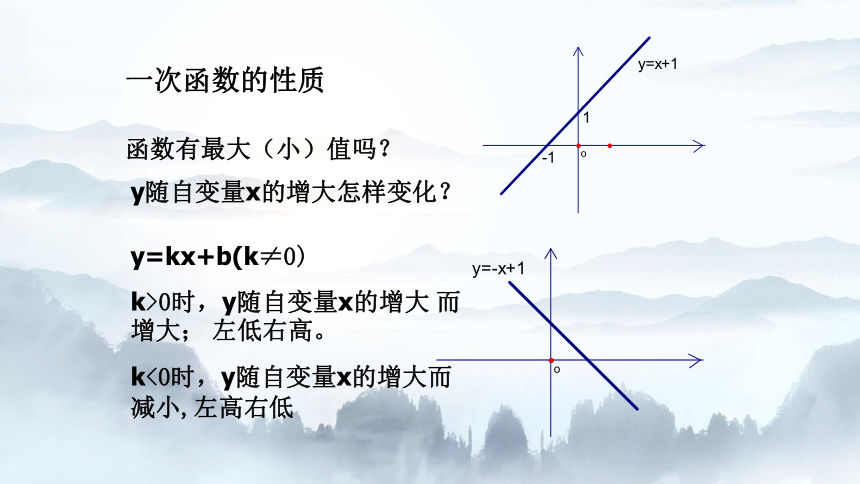
一次函数的性质
y=kx+b(k≠0)
k>0时,y随自变量x的增大 而增大; 左低右高。
k<0时,y随自变量x的增大而减小,左高右低
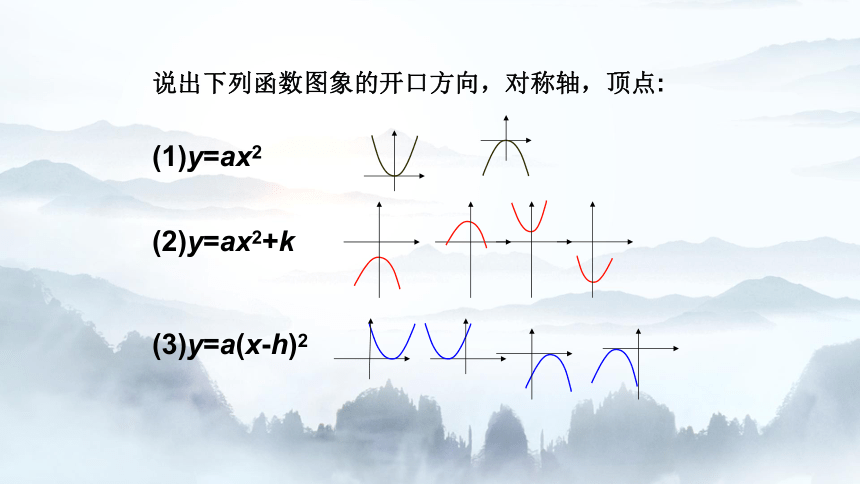
说出下列函数图象的开口方向,对称轴,顶点:
(1)y=ax2
(2)y=ax2+k
(3)y=a(x-h)2
y= 2(x+3)2-2
画出下列函数图象,并说出抛物线的最大值或最小值各是多少及增减性如何?
y= 2(x-3)2+3
y= 2(x-2)2-1
y= 3(x+1)2+1
新知探究
y=a(x-h)2 +k(a≠0) a>0 a<0
对称轴
增
减
性
极值
x=h
x=h
当x当x>h时,y随着x的增大而增大.
当x当x>h时,y随着x的增大而减小.
x=h时,y最小值=k
x=h时,y最大值=k
归纳
例 已知二次函数 .
(1)当自变量x在什么范围内取值时,y随x的增大而增大?在什么范围内取值时,y随x的增大而减小?
(2)这个二次函数有最大值还是最小值?如果有,当x在何值时,函数取得最大值或最小值?并求出最大值或最小值.
解:
(1)因为
所以图象的顶点坐标为(1,3).
因为抛物线开口向下,所以当x<1时,y随x的增大而增大;当x>1时,y随x的增大而减小.
(2)因为抛物线开口向下,顶点坐标为(1,3),所以当x=1时,这个二次函数有最大值3.
通过配方,写出下列抛物线的增减性和最值.
(1)y=x2+4x; (2)y=2x2-4x;
(3)y=-3x2+6x-5;(4) y=x2-8x+5.
解:
(1)x>-2时,y随x的增大而增大;
x<-2时,y随x的增大而减小;
x=-2时,取得最小值,最小值为-4.
(2)x>1时,y随x的增大而增大;
x<1时,y随x的增大而减小;
x=1时,取得最小值,最小值为-2.
巩固练习
(4)x>4时,y随x的增大而增大;
x<4时,y随x的增大而减小;
x=4时,取得最小值,最小值为-11.
(3)x>1时,y随x的增大而减小;
x<1时,y随x的增大而增大;
x=1时,取得最大值,最大值为-2.
x
y
O
x
y
O
a>0
a<0
函数图像
二次函数y=ax2+bx+c的图像和性质如下:
(a>0)
(a<0)
函数增
减情况
当x> 时,函数值
y随x值增大而 ;
当x< 时,函数值
y随x值增大而 .
增大
减小
当x> 时,函数值
y随x值增大而 ;
当x< 时,函数值
y随x值增大而 .
减小
增大
函数
最值
当x= 时,函数值
取得最小值,y最小值=
.
当x= 时,函数值
取得最大值,y最大值=
.
19.3二次函数的性质
复习引入
观察函数y= x+1,y= -x+1 的图象,
函数有最大(小)值吗?y随自变量x
的增大怎样变化?
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时, 开口向上;
当a<0时,开口向下;
(2)对称轴是直线x=h;
(3)顶点是(h,k).
函数有最大(小)值吗?
y随自变量x的增大怎样变化?
一次函数的性质
y=kx+b(k≠0)
k>0时,y随自变量x的增大 而增大; 左低右高。
k<0时,y随自变量x的增大而减小,左高右低
说出下列函数图象的开口方向,对称轴,顶点:
(1)y=ax2
(2)y=ax2+k
(3)y=a(x-h)2
y= 2(x+3)2-2
画出下列函数图象,并说出抛物线的最大值或最小值各是多少及增减性如何?
y= 2(x-3)2+3
y= 2(x-2)2-1
y= 3(x+1)2+1
新知探究
y=a(x-h)2 +k(a≠0) a>0 a<0
对称轴
增
减
性
极值
x=h
x=h
当x
当x
x=h时,y最小值=k
x=h时,y最大值=k
归纳
例 已知二次函数 .
(1)当自变量x在什么范围内取值时,y随x的增大而增大?在什么范围内取值时,y随x的增大而减小?
(2)这个二次函数有最大值还是最小值?如果有,当x在何值时,函数取得最大值或最小值?并求出最大值或最小值.
解:
(1)因为
所以图象的顶点坐标为(1,3).
因为抛物线开口向下,所以当x<1时,y随x的增大而增大;当x>1时,y随x的增大而减小.
(2)因为抛物线开口向下,顶点坐标为(1,3),所以当x=1时,这个二次函数有最大值3.
通过配方,写出下列抛物线的增减性和最值.
(1)y=x2+4x; (2)y=2x2-4x;
(3)y=-3x2+6x-5;(4) y=x2-8x+5.
解:
(1)x>-2时,y随x的增大而增大;
x<-2时,y随x的增大而减小;
x=-2时,取得最小值,最小值为-4.
(2)x>1时,y随x的增大而增大;
x<1时,y随x的增大而减小;
x=1时,取得最小值,最小值为-2.
巩固练习
(4)x>4时,y随x的增大而增大;
x<4时,y随x的增大而减小;
x=4时,取得最小值,最小值为-11.
(3)x>1时,y随x的增大而减小;
x<1时,y随x的增大而增大;
x=1时,取得最大值,最大值为-2.
x
y
O
x
y
O
a>0
a<0
函数图像
二次函数y=ax2+bx+c的图像和性质如下:
(a>0)
(a<0)
函数增
减情况
当x> 时,函数值
y随x值增大而 ;
当x< 时,函数值
y随x值增大而 .
增大
减小
当x> 时,函数值
y随x值增大而 ;
当x< 时,函数值
y随x值增大而 .
减小
增大
函数
最值
当x= 时,函数值
取得最小值,y最小值=
.
当x= 时,函数值
取得最大值,y最大值=
.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
