2022年秋青岛版初中数学九年级上册 2.4 解直角三角形 课件(共16张PPT)
文档属性
| 名称 | 2022年秋青岛版初中数学九年级上册 2.4 解直角三角形 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 827.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 22:10:50 | ||
图片预览





文档简介
(共16张PPT)
2.4 解直角三角形
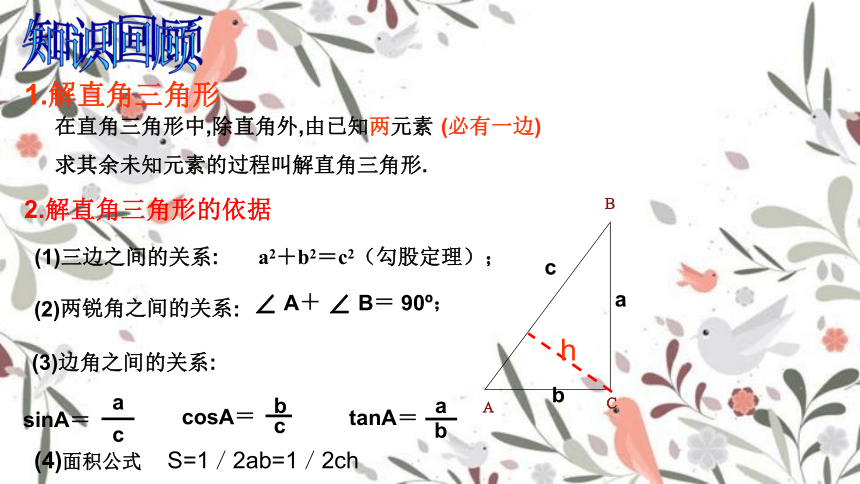
在直角三角形中,除直角外,由已知两元素
求其余未知元素的过程叫解直角三角形.
1.解直角三角形
(1)三边之间的关系:
a2+b2=c2(勾股定理);
2.解直角三角形的依据
(2)两锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
A
C
B
a
b
c
tanA=
a
b
sinA=
a
c
cosA=
b
c
(必有一边)
(4)面积公式 S=1/2ab=1/2ch
h
复习
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数 30° 45° 60°
sin a
cos a
tan a
对于sinα与tanα,角度越大,函数值也越大;(带正)
对于cosα,角度越大,函数值越小。
已知直角三角形的两个元素(至少一个是边),熟练解直角三角形。
通过将非直角三角形问题转化为解直角三角形问题,感悟转化和分类讨论的数学思想。
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
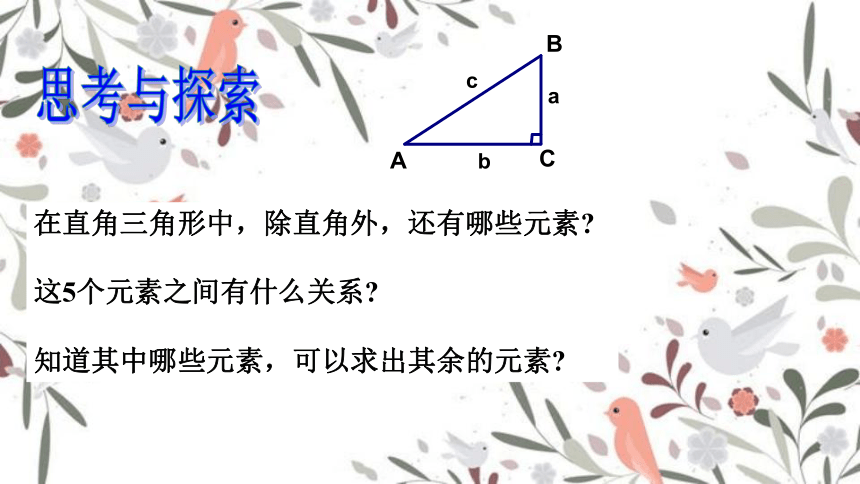
在直角三角形中,我们把两个锐角、三条边称为直角三角形的五个元素.
图中∠A,∠B,a,b,c即为直角三角形的五个元素.
锐角三角比
课时导入
在直角三角形中,除直角外,还有哪些元素
这5个元素之间有什么关系
知道其中哪些元素,可以求出其余的元素
答案: 米
如图,直升飞机在长400米的跨江大桥AB的上方P点处,且A、B、O三点在一条直线上,在大桥的两端测得飞机的仰角分别为30°和45 °,求飞机的高度PO .
A
B
O
30°
45°
400米
P
x
x
例:如图,在△ABC中,已知∠ACB=135°,BC=4,求AC边上的高.
添加条件:如图,在△ABC中,已知∠ACB=135°,BC=4,∠A=30°,求AC边的长.
知道五个元素中的几个,就可以求其余元素?
探究
必须已知除直角外的两个元素(至少有一个是边).
已知两边:a.两直角边;b.一直角边和斜边.
已知一边和一锐角:a.一直角边和一锐角;b.斜边和一锐角.
在直角三角形中,由已知元素求未知元素的过程,叫
解直角三角形
解直角三角形的依据
A
C
B
a
b
c
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
新知识
(4)面积公式:
在山脚C处测得山顶A的仰角为45°。问题如下:
1)沿着水平地面向前300米到达D点,在D点测得山顶A的仰角为600 , 求山高AB。
D
A
B
C
x
45°
60°
300米
AB还可以怎样表示?
那么这是先利用那个三角形?
若设AB为x,又该怎样找关系?
x
解直角
三角形
∠A+ ∠ B=90°
a2+b2=c2
三角函数
关系式
解直角三角形:
由已知元素求未知元素的过程
直角三角形中,
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
已知一边一角如何解直角三角形?
2、如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=45°,∠ACB=30°,量得BC长为30米.求河的宽度(即求△ABC中BC边上的高);
解:过点A作AD⊥BC交BC于点D
在Rt△ABD中,∠ADB=90°,∠ABC=45°
∴∠BAD=45° ∴BD=AD
设BD=AD=x米,在Rt△ACD中,∠ADC=90°, AD=x米,∠ACB=30°
tan ∠ACB= ∴CD= x米
∵BD+CD=BC,BC=30米
∴x+ x=30
解得:x=
∴河的宽度为 米
总 结
在直角三角形的6个元素中,直角是已知元素,如果
再知道一条边和第三 个元素,那么这个三角形的所有元
素就都可以确定下来.
解直角三角形
由直角三角形中已知的元素求出未知元素的过程,叫作解直角三角形.
两边:两直角边或斜边、一直角边
一边一角:直角边、一锐角或斜边、一锐角
课堂小结
今天的课到此结束。如果你有任何问题,你可以问老师。我相信每个人都能学会这节课的内容,对今后的学习会有很大的帮助
2.4 解直角三角形
在直角三角形中,除直角外,由已知两元素
求其余未知元素的过程叫解直角三角形.
1.解直角三角形
(1)三边之间的关系:
a2+b2=c2(勾股定理);
2.解直角三角形的依据
(2)两锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
A
C
B
a
b
c
tanA=
a
b
sinA=
a
c
cosA=
b
c
(必有一边)
(4)面积公式 S=1/2ab=1/2ch
h
复习
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数 30° 45° 60°
sin a
cos a
tan a
对于sinα与tanα,角度越大,函数值也越大;(带正)
对于cosα,角度越大,函数值越小。
已知直角三角形的两个元素(至少一个是边),熟练解直角三角形。
通过将非直角三角形问题转化为解直角三角形问题,感悟转化和分类讨论的数学思想。
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
在直角三角形中,我们把两个锐角、三条边称为直角三角形的五个元素.
图中∠A,∠B,a,b,c即为直角三角形的五个元素.
锐角三角比
课时导入
在直角三角形中,除直角外,还有哪些元素
这5个元素之间有什么关系
知道其中哪些元素,可以求出其余的元素
答案: 米
如图,直升飞机在长400米的跨江大桥AB的上方P点处,且A、B、O三点在一条直线上,在大桥的两端测得飞机的仰角分别为30°和45 °,求飞机的高度PO .
A
B
O
30°
45°
400米
P
x
x
例:如图,在△ABC中,已知∠ACB=135°,BC=4,求AC边上的高.
添加条件:如图,在△ABC中,已知∠ACB=135°,BC=4,∠A=30°,求AC边的长.
知道五个元素中的几个,就可以求其余元素?
探究
必须已知除直角外的两个元素(至少有一个是边).
已知两边:a.两直角边;b.一直角边和斜边.
已知一边和一锐角:a.一直角边和一锐角;b.斜边和一锐角.
在直角三角形中,由已知元素求未知元素的过程,叫
解直角三角形
解直角三角形的依据
A
C
B
a
b
c
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
新知识
(4)面积公式:
在山脚C处测得山顶A的仰角为45°。问题如下:
1)沿着水平地面向前300米到达D点,在D点测得山顶A的仰角为600 , 求山高AB。
D
A
B
C
x
45°
60°
300米
AB还可以怎样表示?
那么这是先利用那个三角形?
若设AB为x,又该怎样找关系?
x
解直角
三角形
∠A+ ∠ B=90°
a2+b2=c2
三角函数
关系式
解直角三角形:
由已知元素求未知元素的过程
直角三角形中,
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
已知一边一角如何解直角三角形?
2、如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=45°,∠ACB=30°,量得BC长为30米.求河的宽度(即求△ABC中BC边上的高);
解:过点A作AD⊥BC交BC于点D
在Rt△ABD中,∠ADB=90°,∠ABC=45°
∴∠BAD=45° ∴BD=AD
设BD=AD=x米,在Rt△ACD中,∠ADC=90°, AD=x米,∠ACB=30°
tan ∠ACB= ∴CD= x米
∵BD+CD=BC,BC=30米
∴x+ x=30
解得:x=
∴河的宽度为 米
总 结
在直角三角形的6个元素中,直角是已知元素,如果
再知道一条边和第三 个元素,那么这个三角形的所有元
素就都可以确定下来.
解直角三角形
由直角三角形中已知的元素求出未知元素的过程,叫作解直角三角形.
两边:两直角边或斜边、一直角边
一边一角:直角边、一锐角或斜边、一锐角
课堂小结
今天的课到此结束。如果你有任何问题,你可以问老师。我相信每个人都能学会这节课的内容,对今后的学习会有很大的帮助
