2022年秋青岛版初中数学九年级上册 2.5.3 解直角三角形的应用 3 课件(共15张PPT)
文档属性
| 名称 | 2022年秋青岛版初中数学九年级上册 2.5.3 解直角三角形的应用 3 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 22:11:35 | ||
图片预览






文档简介
(共15张PPT)
2.5.3 解直角三角形的应用 3
1.利用解直角三角形的知识解决实际问题的一般步骤是:
(1)将实际问题抽象为_ _ __(画出平面图形,转化为_ _ __的问题).
(2)根据条件的特点,适当选用锐角三角函数等去_________.
(3)得到_____ ___的答案.(4)得到__ ______的答案.
2.如图,小明从A地沿北偏东30°方向走 到B地,再从B地向正南方向走200 m到C地,此时小明离A地_______ m
3.如图,水库大坝的横断面是梯形,坝顶宽6 m,坝高24 m,斜坡AB的坡角A为45°,斜坡CD的坡角D的正切值为 ,则坡底AD的长为( )
A. 42 m B. C.78 m D.
解直角三角形
解直角三角形
数学问题
数学问题
实际问题
100
C
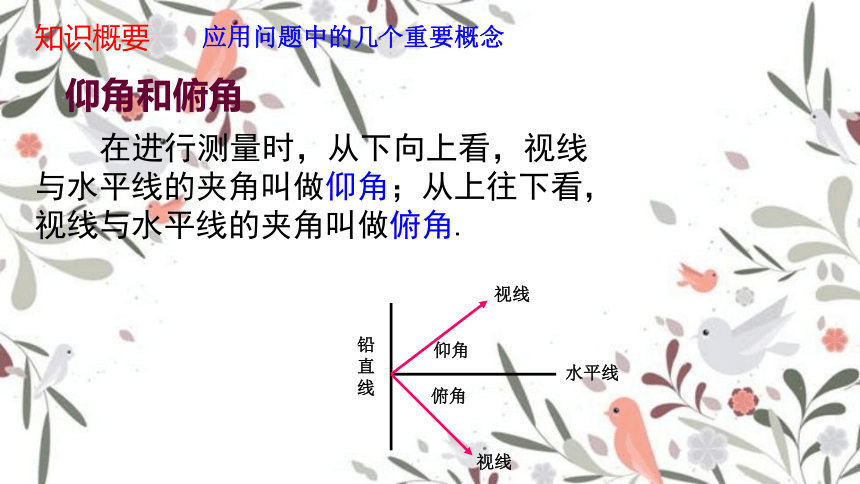
仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
知识概要
应用问题中的几个重要概念
解决直角三角形的应用思路
把实际问题转化为解直角三角形的问题,关键是找出实际问题中的直角三角形之间数量关系,是解决与直角三角形有关的实际问题的重要工具。
某探险者某天到达如图所示的点A 处时,他准备估算出离他的目的地——海拔为3 500 m 的山峰顶点B处的水平距离. 他能想出一个可行的办法吗?
海中一小岛周围3.8海里内有暗礁。军舰由西向东航行,望见这岛在北偏东75°,航行8海里后,望见这岛在北偏东60°,如果军舰不改变航向,继续前进,有没有触礁的危险?
点拔:方位角问题的实际应用题解法:
直接或间接把问题放在直角三角形中,解题时应善于发现直角三角形,用三角函数等知识解决问题。
解:作ND⊥CB交AC于N,
由题意,知∠ACB=15°,∠NDA=60°,
∴∠ADB=90°-∠NDA=30°,
又∠ADB=∠ACB+∠CAD,
∴∠CAD=30°-15°=15°,
∴∠ACB=∠CAD,即AD=CD=8,
而4>3.8,
所以没有触礁的危险。
坡度通常写成1∶m的形式,如i=1∶6.
坡面与水平面的夹角叫做坡角,记作a,有i= =tan a
显然,坡度越大,坡角a就越大,坡面就越陡.
在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
如图:坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面坡度(或坡比).记作i,即 I = .
坡度(坡比),坡角的概念
如图,如果测得点A的海拔AE为1600m, 仰角 求出A,B两点之间的水平距离AC(结果保留整数).
A. B. C. D.
1.王英同学从A地沿北偏西60°方向走100 m到B地,再从B地向正南方向走200 m到C地,此时王英同学离A地( )
2、在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200 m到达B地,再沿北偏东30°方向走,恰能达目的地C(如图),那么,由此可知,B,C两地相距_ _m.
3、如右上图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1∶1.5,则坝底AD的长度为( )
D
A.26米 B.28米 C.30米 D.46米
200
D
2题
3题
如图,从山脚到山顶有两条路AB与BD,问哪条路比较陡?
右边的路BD陡些.
如何用数量来刻画哪条路陡呢?
如上图所示,从山坡脚下点 A 上坡走到点B时,升高的高度h(即线段BC的长度)与水平前进的距离l(即线段AC 的长度)的比叫作坡度,用字母i表示,即
(坡度通常写成1:m的形式).
坡度越大,山坡越陡.
在上图中,∠BAC 叫作坡角(即山坡与地平面的
夹角),记作 ,显然,坡度等于坡角的正切,即
(2014·泸州)海中两个灯塔A,B,其中B位于A的正东方向上,渔船跟踪鱼群由西向东航行,在点C处测得灯塔A在西北方向上,灯塔B在北偏东30°方向上,渔船不改变航向继续向东航行30海里到达点D,这时测得灯塔A在北偏西60°方向上,求灯塔A,B间的距离.(计算结果用根号表示,不取近似值)
必做题
如图,河流的两岸PQ,MN互相平行,河岸PQ上有一排小树,已知相邻 两树之间的距CD=50米,某人在河岸MN的A处测的∠DAN=35°,然后沿河岸走了120米到达B处,测的∠CBN=70°,求河流的宽度CE(结果保留两个有效数字)。(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
1. 在直角三角形中,任一锐角的三角函数只与角
的大小有关,而与直角三角形的大小无关.
2. 在直角三角形中,已知一条边和一个角,或已知
两条边,就可以求出其他的边和角.
有些关于图形的实际问题,我们可以结和已知条件,
恰当地构造出直角三角形,画出图形,将实际问题
转化为解直角三角形的问题.
3.
课堂小结
今天的课到此结束。如果你有任何问题,你可以问老师。我相信每个人都能学会这节课的内容,对今后的学习会有很大的帮助
2.5.3 解直角三角形的应用 3
1.利用解直角三角形的知识解决实际问题的一般步骤是:
(1)将实际问题抽象为_ _ __(画出平面图形,转化为_ _ __的问题).
(2)根据条件的特点,适当选用锐角三角函数等去_________.
(3)得到_____ ___的答案.(4)得到__ ______的答案.
2.如图,小明从A地沿北偏东30°方向走 到B地,再从B地向正南方向走200 m到C地,此时小明离A地_______ m
3.如图,水库大坝的横断面是梯形,坝顶宽6 m,坝高24 m,斜坡AB的坡角A为45°,斜坡CD的坡角D的正切值为 ,则坡底AD的长为( )
A. 42 m B. C.78 m D.
解直角三角形
解直角三角形
数学问题
数学问题
实际问题
100
C
仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
知识概要
应用问题中的几个重要概念
解决直角三角形的应用思路
把实际问题转化为解直角三角形的问题,关键是找出实际问题中的直角三角形之间数量关系,是解决与直角三角形有关的实际问题的重要工具。
某探险者某天到达如图所示的点A 处时,他准备估算出离他的目的地——海拔为3 500 m 的山峰顶点B处的水平距离. 他能想出一个可行的办法吗?
海中一小岛周围3.8海里内有暗礁。军舰由西向东航行,望见这岛在北偏东75°,航行8海里后,望见这岛在北偏东60°,如果军舰不改变航向,继续前进,有没有触礁的危险?
点拔:方位角问题的实际应用题解法:
直接或间接把问题放在直角三角形中,解题时应善于发现直角三角形,用三角函数等知识解决问题。
解:作ND⊥CB交AC于N,
由题意,知∠ACB=15°,∠NDA=60°,
∴∠ADB=90°-∠NDA=30°,
又∠ADB=∠ACB+∠CAD,
∴∠CAD=30°-15°=15°,
∴∠ACB=∠CAD,即AD=CD=8,
而4>3.8,
所以没有触礁的危险。
坡度通常写成1∶m的形式,如i=1∶6.
坡面与水平面的夹角叫做坡角,记作a,有i= =tan a
显然,坡度越大,坡角a就越大,坡面就越陡.
在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
如图:坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面坡度(或坡比).记作i,即 I = .
坡度(坡比),坡角的概念
如图,如果测得点A的海拔AE为1600m, 仰角 求出A,B两点之间的水平距离AC(结果保留整数).
A. B. C. D.
1.王英同学从A地沿北偏西60°方向走100 m到B地,再从B地向正南方向走200 m到C地,此时王英同学离A地( )
2、在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200 m到达B地,再沿北偏东30°方向走,恰能达目的地C(如图),那么,由此可知,B,C两地相距_ _m.
3、如右上图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1∶1.5,则坝底AD的长度为( )
D
A.26米 B.28米 C.30米 D.46米
200
D
2题
3题
如图,从山脚到山顶有两条路AB与BD,问哪条路比较陡?
右边的路BD陡些.
如何用数量来刻画哪条路陡呢?
如上图所示,从山坡脚下点 A 上坡走到点B时,升高的高度h(即线段BC的长度)与水平前进的距离l(即线段AC 的长度)的比叫作坡度,用字母i表示,即
(坡度通常写成1:m的形式).
坡度越大,山坡越陡.
在上图中,∠BAC 叫作坡角(即山坡与地平面的
夹角),记作 ,显然,坡度等于坡角的正切,即
(2014·泸州)海中两个灯塔A,B,其中B位于A的正东方向上,渔船跟踪鱼群由西向东航行,在点C处测得灯塔A在西北方向上,灯塔B在北偏东30°方向上,渔船不改变航向继续向东航行30海里到达点D,这时测得灯塔A在北偏西60°方向上,求灯塔A,B间的距离.(计算结果用根号表示,不取近似值)
必做题
如图,河流的两岸PQ,MN互相平行,河岸PQ上有一排小树,已知相邻 两树之间的距CD=50米,某人在河岸MN的A处测的∠DAN=35°,然后沿河岸走了120米到达B处,测的∠CBN=70°,求河流的宽度CE(结果保留两个有效数字)。(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
1. 在直角三角形中,任一锐角的三角函数只与角
的大小有关,而与直角三角形的大小无关.
2. 在直角三角形中,已知一条边和一个角,或已知
两条边,就可以求出其他的边和角.
有些关于图形的实际问题,我们可以结和已知条件,
恰当地构造出直角三角形,画出图形,将实际问题
转化为解直角三角形的问题.
3.
课堂小结
今天的课到此结束。如果你有任何问题,你可以问老师。我相信每个人都能学会这节课的内容,对今后的学习会有很大的帮助
