1.4.1 第2课时 有理数加法的运算律 课件(共23页)
文档属性
| 名称 | 1.4.1 第2课时 有理数加法的运算律 课件(共23页) |  | |
| 格式 | pptx | ||
| 文件大小 | 999.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 18:34:22 | ||
图片预览





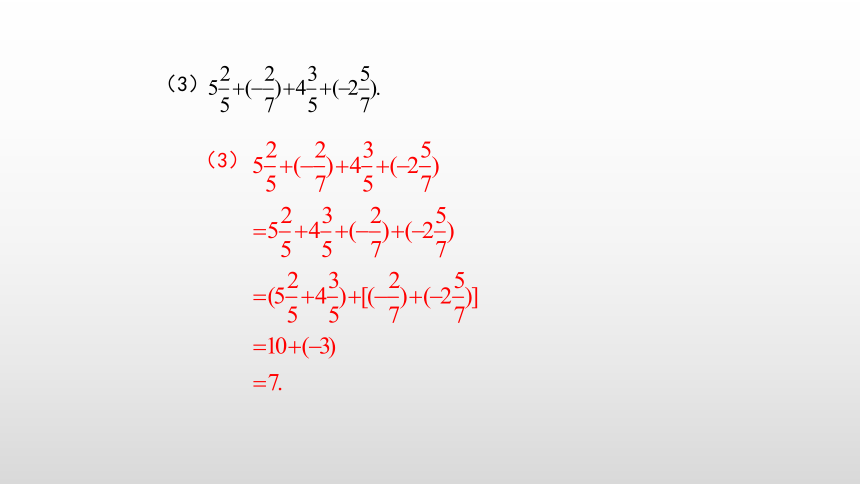
文档简介
(共23张PPT)
1.4 有理数的加法和减法
1.4.1 有理数的加法
第2课时 有理数加法的运算律
湘教版七年级上册
教学目标
1.能概括出有理数的加法交换律和结合律.
2.灵活熟练地运用加法交换律、结合律简化运算(重点、难点)
导入新课
情境引入
学习了有理数的加法运算法则后,爱探索的小明发现,(-3)+(-6)与(-6)+(-3)相等,8+(-3)与(-3)+8也相等,于是他想:是不是任意的两个加数,交换它们的位置后,和仍然相等呢?同学们你们认为呢?
3
﹢
-5
﹦
__
-2
-5
3
﹢
﹦
__
-2
讲授新课
加法运算律
一
观察与思考
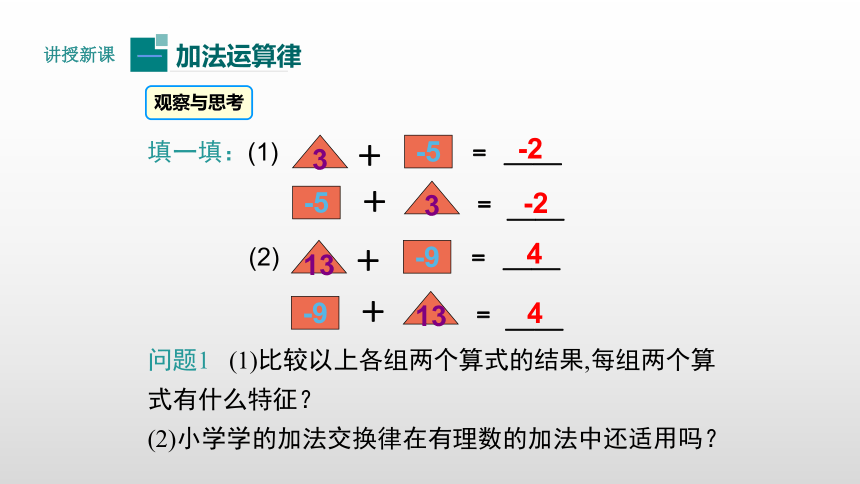
填一填:(1)
问题1 (1)比较以上各组两个算式的结果,每组两个算式有什么特征?
(2)小学学的加法交换律在有理数的加法中还适用吗?
13
﹢
-9
﹦
__
4
-9
13
﹢
﹦
__
4
(2)
3
-5
﹢
﹦
__
)
-7
-9
(
﹢
3
-5
﹢
﹢
﹦
__
-7
-9
(
)
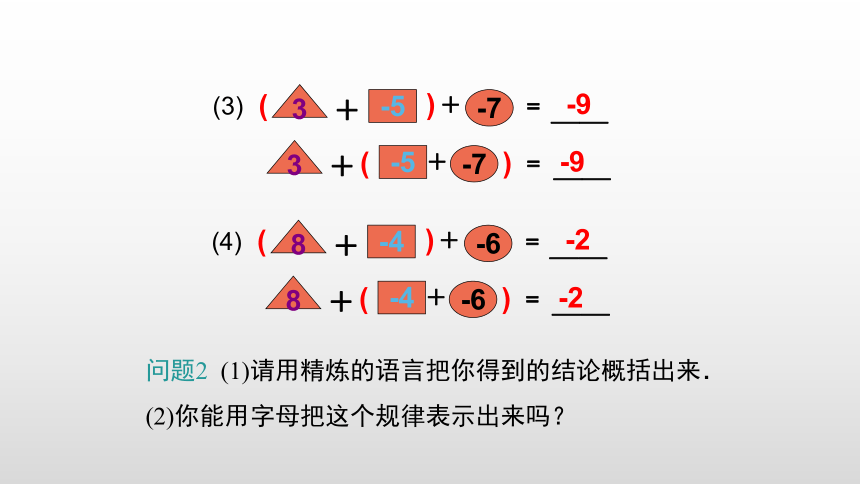
(3)
8
-4
﹢
﹦
__
)
-6
-2
(
﹢
8
-4
﹢
﹢
﹦
__
-6
-2
(
)
(4)
问题2 (1)请用精炼的语言把你得到的结论概括出来.
(2)你能用字母把这个规律表示出来吗?
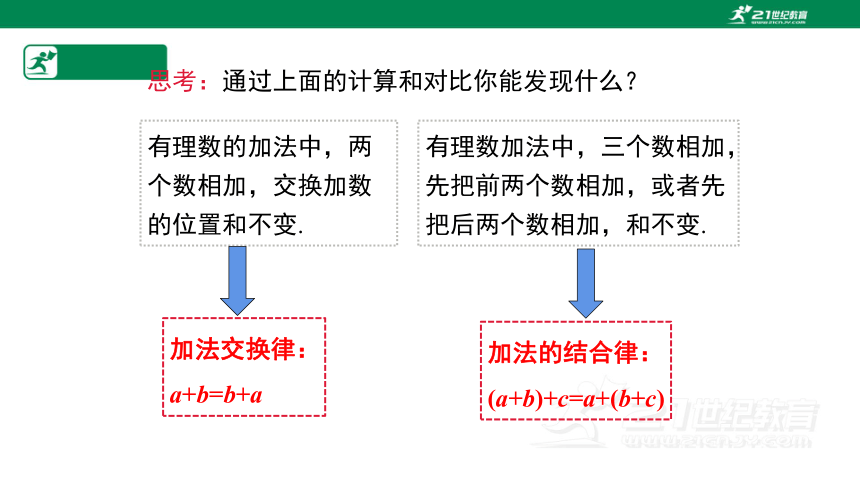
有理数的加法中,两个数相加,交换加数的位置和不变.
加法交换律:
a+b=b+a
有理数加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法的结合律:
(a+b)+c=a+(b+c)
思考:通过上面的计算和对比你能发现什么?
解(1) 16+(-25)+24+(-32)
=16+24+(-25)+(-32) (加法交换律)
=(16+24)+[(-25)+(-32)] (加法结合律)
=40+(-57 ) (同号相加法则)
=-17 (异号相加法则)
例1 计算:
(1)16+(-25)+24+(-32) (2)31 +(-28)+ 28 + 69
(2)31 +(-28)+ 28 + 69
=31 + 69 + [(-28)+ 28 ] (加法交换律和结合律 )
=100+0
=100
例2 计算:
(1)(-32)+7+(-8); (2)4.37+(-8)+(-4.37);
(3)
解:
(1)
(2)
(3)
(3)
常用的三个规律:
1.有相反数的可先把相反数相加,能凑整的可先凑整;
2.有分母相同的,可先把分母相同的数结合相加;
3.然后把正数或负数分别结合在一起相加.
小组讨论:你是抓住数的什么特点使计算简化的?
依据是什么?
(1)(-2.48)+4.33+(-7.52)+(-4.33)
(2)
例3 计算:
解:原式=[(-2.48)+(-7.52)]+[(+4.33)+(-4.33)]
=(-10)+0
=-10
(1) 23+(-17)+6+(-22);
(2) (-2)+3+1+(-3)+2+(-4);
(3) (-7)+(-6.5)+(-3)+6.5.
练一练
-10
-3
-10
加法运算律的应用
二
例4 某台自动存取款机在某时段内处理了以下6项现款储蓄业务:
存入200元、支出800元、支出1000元、
存入2500元、支出500元、支出300元.
问该自动存取款机在这一时段内现款增加或减少了多少元?
解:记存入为正,则由题意可得
答:该自动存取款机在这一时段内现款增加了100元.
例5 某公路养护小组乘车沿南北方向巡视维修,某天早晨他们从A地出发,晚上最后到达B地,约定向北为正方向,当天的行驶记录如下(单位:千米):
+18,-9,+7,-14,+13,-6,-8.
(1)B地在A地何方,相距多少千米?
解:(1)(+18)+(-9)+(+7)+(-14)+(+13)+(-6)+(-8)=[(+18)+(+7)+(+13)]+[(-9)+(-14)+(-6)+(-8)]=38+(-37)=1(千米).
故B地在A地正北方,相距1千米;
例5 某公路养护小组乘车沿南北方向巡视维修,某天早晨他们从A地出发,晚上最后到达B地,约定向北为正方向,当天的行驶记录如下(单位:千米):
+18,-9,+7,-14,+13,-6,-8.
(2)若汽车行驶1千米耗油0.6升,求该天耗油多少升.
解:(18+9+7+14+13+6+8)×0.6=45(升).
答:该天耗油45升.
当堂练习
1.计算:
(1)23+(-17)+6+(-22)
=(23+6)+[(-17)+(-22)]
=29-39
=-10
=(3+1+2)+[(-2)+(-3)+(-4)]
=6-9
=-3
(2)(-2)+3+1+(-3)+2+(-4)
2.计算:
=-2
3.10筐苹果,以每筐30千克为基准,超过的千克数记作正数,不足的千克数记作负数,记录如下:
2, -4, 2.5, 3, -0.5, 1.5, 3, -1, 0, -2.5.
问这10筐苹果总共重多少千克?
=8+(-4)
解:根据题意得
2+(-4)+2.5+3+(-0.5)+1.5+3+(-1)+0+(-2.5)
=(2+3+3)+(-4)+[2.5+(-2.5)]+[(-0.5)+(-1)+1.5]
=4
所以这10筐苹果总重量为:30×10+4=304(千克)
4.每袋小麦的标准重量为90千克,10袋小麦称重记录如图所示,与标准重量比较,10袋小麦总计超过多少千克或不足多少千克?10袋小麦的总重量是多少?
91
91
91.3
88.7
91.5
89
91.2
88.8
91.8
91.1
解法一: 这10袋小麦的总质量为91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1=905.4(千克) .
10袋小麦总计超过标准重量为905.4-90×10=5.4(千克).
解法二:每袋小麦超过标准重量的千克数记作正数,不足的千克数记作负数,10袋小麦对应的数为+1,+1,+1.5,-1,+1.2,+1.3,-1.3,-1.2,+1.8,+1.1.
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)+1.8+1.1
=[1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)]+ (1+1.5+1.8+1.1)=5.4
90×10+5.4=905.4(千克)
答:10袋小麦总计超过标准重量5.4千克,总重量是905.4千克.
课堂小结
有理数加法的运算律
交换律
结合律
应用
a+b=_____
b+a
(a+b)+c=__________
a+(b+c)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.4 有理数的加法和减法
1.4.1 有理数的加法
第2课时 有理数加法的运算律
湘教版七年级上册
教学目标
1.能概括出有理数的加法交换律和结合律.
2.灵活熟练地运用加法交换律、结合律简化运算(重点、难点)
导入新课
情境引入
学习了有理数的加法运算法则后,爱探索的小明发现,(-3)+(-6)与(-6)+(-3)相等,8+(-3)与(-3)+8也相等,于是他想:是不是任意的两个加数,交换它们的位置后,和仍然相等呢?同学们你们认为呢?
3
﹢
-5
﹦
__
-2
-5
3
﹢
﹦
__
-2
讲授新课
加法运算律
一
观察与思考
填一填:(1)
问题1 (1)比较以上各组两个算式的结果,每组两个算式有什么特征?
(2)小学学的加法交换律在有理数的加法中还适用吗?
13
﹢
-9
﹦
__
4
-9
13
﹢
﹦
__
4
(2)
3
-5
﹢
﹦
__
)
-7
-9
(
﹢
3
-5
﹢
﹢
﹦
__
-7
-9
(
)
(3)
8
-4
﹢
﹦
__
)
-6
-2
(
﹢
8
-4
﹢
﹢
﹦
__
-6
-2
(
)
(4)
问题2 (1)请用精炼的语言把你得到的结论概括出来.
(2)你能用字母把这个规律表示出来吗?
有理数的加法中,两个数相加,交换加数的位置和不变.
加法交换律:
a+b=b+a
有理数加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法的结合律:
(a+b)+c=a+(b+c)
思考:通过上面的计算和对比你能发现什么?
解(1) 16+(-25)+24+(-32)
=16+24+(-25)+(-32) (加法交换律)
=(16+24)+[(-25)+(-32)] (加法结合律)
=40+(-57 ) (同号相加法则)
=-17 (异号相加法则)
例1 计算:
(1)16+(-25)+24+(-32) (2)31 +(-28)+ 28 + 69
(2)31 +(-28)+ 28 + 69
=31 + 69 + [(-28)+ 28 ] (加法交换律和结合律 )
=100+0
=100
例2 计算:
(1)(-32)+7+(-8); (2)4.37+(-8)+(-4.37);
(3)
解:
(1)
(2)
(3)
(3)
常用的三个规律:
1.有相反数的可先把相反数相加,能凑整的可先凑整;
2.有分母相同的,可先把分母相同的数结合相加;
3.然后把正数或负数分别结合在一起相加.
小组讨论:你是抓住数的什么特点使计算简化的?
依据是什么?
(1)(-2.48)+4.33+(-7.52)+(-4.33)
(2)
例3 计算:
解:原式=[(-2.48)+(-7.52)]+[(+4.33)+(-4.33)]
=(-10)+0
=-10
(1) 23+(-17)+6+(-22);
(2) (-2)+3+1+(-3)+2+(-4);
(3) (-7)+(-6.5)+(-3)+6.5.
练一练
-10
-3
-10
加法运算律的应用
二
例4 某台自动存取款机在某时段内处理了以下6项现款储蓄业务:
存入200元、支出800元、支出1000元、
存入2500元、支出500元、支出300元.
问该自动存取款机在这一时段内现款增加或减少了多少元?
解:记存入为正,则由题意可得
答:该自动存取款机在这一时段内现款增加了100元.
例5 某公路养护小组乘车沿南北方向巡视维修,某天早晨他们从A地出发,晚上最后到达B地,约定向北为正方向,当天的行驶记录如下(单位:千米):
+18,-9,+7,-14,+13,-6,-8.
(1)B地在A地何方,相距多少千米?
解:(1)(+18)+(-9)+(+7)+(-14)+(+13)+(-6)+(-8)=[(+18)+(+7)+(+13)]+[(-9)+(-14)+(-6)+(-8)]=38+(-37)=1(千米).
故B地在A地正北方,相距1千米;
例5 某公路养护小组乘车沿南北方向巡视维修,某天早晨他们从A地出发,晚上最后到达B地,约定向北为正方向,当天的行驶记录如下(单位:千米):
+18,-9,+7,-14,+13,-6,-8.
(2)若汽车行驶1千米耗油0.6升,求该天耗油多少升.
解:(18+9+7+14+13+6+8)×0.6=45(升).
答:该天耗油45升.
当堂练习
1.计算:
(1)23+(-17)+6+(-22)
=(23+6)+[(-17)+(-22)]
=29-39
=-10
=(3+1+2)+[(-2)+(-3)+(-4)]
=6-9
=-3
(2)(-2)+3+1+(-3)+2+(-4)
2.计算:
=-2
3.10筐苹果,以每筐30千克为基准,超过的千克数记作正数,不足的千克数记作负数,记录如下:
2, -4, 2.5, 3, -0.5, 1.5, 3, -1, 0, -2.5.
问这10筐苹果总共重多少千克?
=8+(-4)
解:根据题意得
2+(-4)+2.5+3+(-0.5)+1.5+3+(-1)+0+(-2.5)
=(2+3+3)+(-4)+[2.5+(-2.5)]+[(-0.5)+(-1)+1.5]
=4
所以这10筐苹果总重量为:30×10+4=304(千克)
4.每袋小麦的标准重量为90千克,10袋小麦称重记录如图所示,与标准重量比较,10袋小麦总计超过多少千克或不足多少千克?10袋小麦的总重量是多少?
91
91
91.3
88.7
91.5
89
91.2
88.8
91.8
91.1
解法一: 这10袋小麦的总质量为91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1=905.4(千克) .
10袋小麦总计超过标准重量为905.4-90×10=5.4(千克).
解法二:每袋小麦超过标准重量的千克数记作正数,不足的千克数记作负数,10袋小麦对应的数为+1,+1,+1.5,-1,+1.2,+1.3,-1.3,-1.2,+1.8,+1.1.
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)+1.8+1.1
=[1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)]+ (1+1.5+1.8+1.1)=5.4
90×10+5.4=905.4(千克)
答:10袋小麦总计超过标准重量5.4千克,总重量是905.4千克.
课堂小结
有理数加法的运算律
交换律
结合律
应用
a+b=_____
b+a
(a+b)+c=__________
a+(b+c)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
