教科版(2019)必修 第一册第三章 相互作用 培优课2 力的合成与分解 课件(共30张PPT)
文档属性
| 名称 | 教科版(2019)必修 第一册第三章 相互作用 培优课2 力的合成与分解 课件(共30张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-09-16 14:16:54 | ||
图片预览










文档简介
(共30张PPT)
第二章 力
培优课 力的合成与分解
学习目标 重点难点
1.理解分力与合力的关系.
2.理解利用平行四边形定则求合力.
3.会根据平行四边形定则对力的分解进行讨论.
4.掌握力的正交分解法. 1.力的合成与分解是本节学习的重点.
2.对力的分解讨论是本节学习的难点.
一、力的合成
1.分力与合力从效果上看具有什么关系?
提示:等效替代关系
2.力的合成遵循什么法则?
提示:平行四边形定则
3.两个大小一定的力F1、F2,当其夹角θ由0°逐渐增大到180°的过程中其合力大小如何变化?
提示:逐渐减小
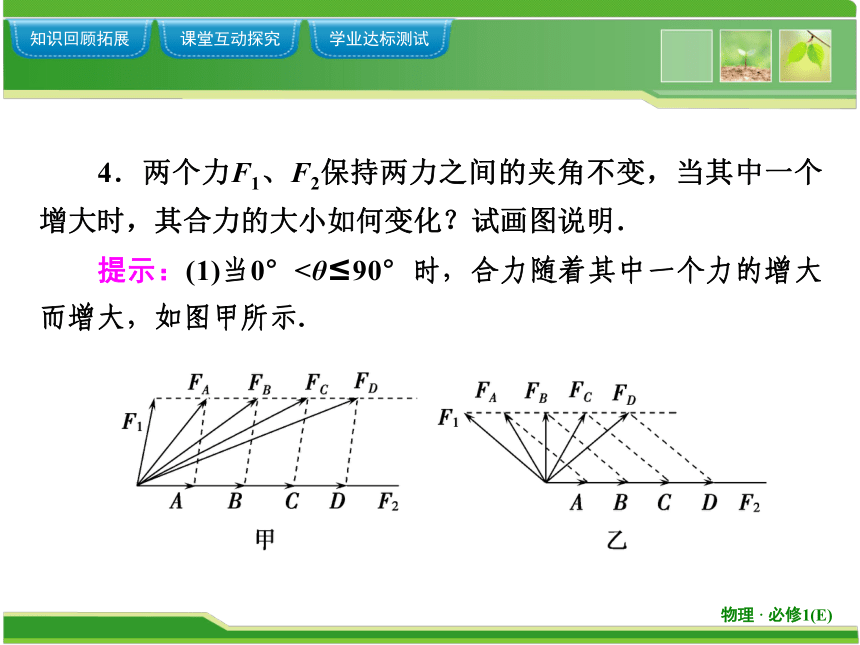
4.两个力F1、F2保持两力之间的夹角不变,当其中一个增大时,其合力的大小如何变化?试画图说明.
提示:(1)当0°<θ≤90°时,合力随着其中一个力的增大而增大,如图甲所示.
(2)当90°<θ≤180°时,若F2增大,其合力先变小,后又逐渐增大,如图乙所示.
故合力可能增大、可能不变、也可能减小
5.怎样确定三个力的合力变化范围?
提示:设三个力大小分别是F1、F2、F3.
(1)其合力的最大值为Fmax=F1+F2+F3.
(2)合力的最小值.
①如果三个力中其中任意一个力的大小在另外两个力的合力范围内,即|F1-F2|≤F3≤F1+F2,则合力最小值可以为零.
②如果不满足①中条件,合力的最小值应为最大的力(设为F1)与另外两个较小的力(设为F2、F3)的差,方向与最大的力(F1)同向,即Fmin=F1-(F2+F3).
二、力的分解
1.力的分解遵循什么法则?
提示:平行四边形定则
2.一个力如果不受条件限制可以分解为多少对不同的分力?
提示:一个力分解为两个力,从理论上讲有无数组解.因为以同一条线段为对角线的平行四边形有无穷多个(如图所示)
3.试分析以下情况下力的分解是否具有唯一性?
(1)已知合力和两个分力的方向.
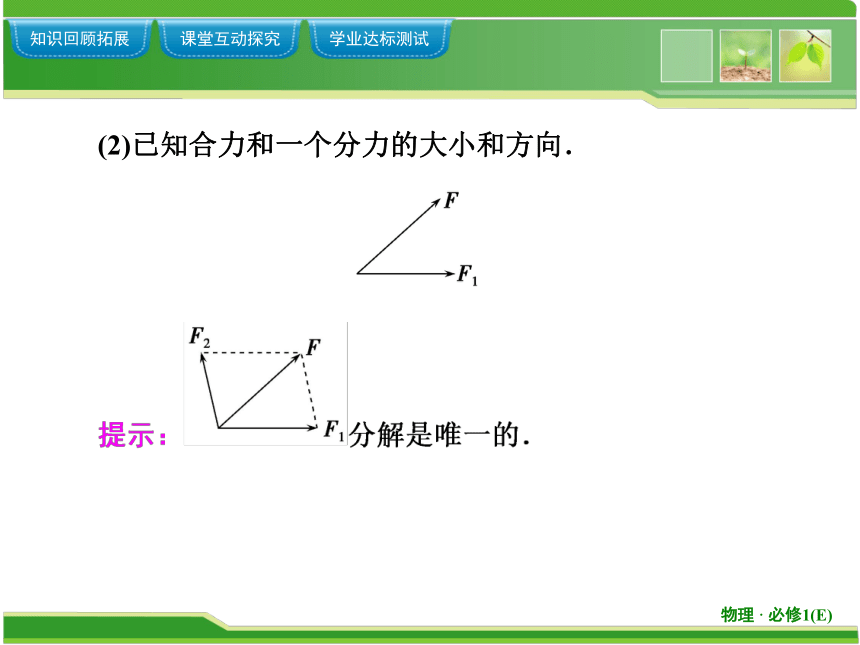
(2)已知合力和一个分力的大小和方向.
(3)已知合力F以及一个分力F1的方向和另一个分力F2的大小时,若F与F1的夹角为α.
提示:
①当Fsin α<F2<F时,有两解,如图甲所示.
②当F2=Fsin α时,有唯一解,如图乙所示.
③当F2<Fsin α时,无解,如图丙所示.
④当F2>F时,有唯一解,如图丁所示.
4.实际问题中,如何分解一个力?
提示:按力的实际效果分解,具体做法是:(1)先根据力的实际作用效果确定两个分力的方向;(2)再根据两个实际分力方向画出平行四边形;(3)最后根据平行四边形和学过的数学知识求出两分力的大小.
三、力的正交分解法
如图所示的三个共点力F1、F2、F3,为求这三个力的合力,试写出用正交分解法求合力的步骤.
提示:具体步骤如下:
(1)建立直角坐标系,以共点力的作用点为坐标原点建立直角坐标系,x轴和y轴的选取原则是使尽量多的力落在坐标轴上;
(2)正交分解各力,即将每一个不在坐标轴上的力分解到坐标轴上,并求出各分力的大小,如图所示;
[解题探究]
(1)如果没有条件限制,F2的最小值是多少?
提示:当F2与F1垂直时,F2的值最小为Fsin 30°
(2)因F2>Fsin 30°,其方向有几种可能?
提示:两种
解析:由平行四边形定则画出力的分解示意图.
答案:AD
如图所示,一小球放置在木板与竖直墙面之间.设球对墙的压力大小为N1,球对木板的压力大小为N2.以木板与墙连接点所形成的水平直线为轴,将木板从图示位置开始缓慢地转到水平位置.不计摩擦,在此过程中( )
A.N1始终减小,N2始终增大
B.N1始终减小,N2始终减小
C.N1先增大后减小,N2始终减小
D.N1先增大后减小,N2先减小后增大
[解题探究]
(1)小球的重力产生了哪两个效果?
提示:对墙和木板产生了压力
(2)当木板与墙的夹角增大时,小球对墙的压力方向变吗?
提示:不变
法二:图解法
木板转动过程中,重力的两个分力中N1的方向不变,N2的方向始终与木板垂直,可作出如图所示的示意图.由图可知N1、N2均减小.
答案:B
[题后总结] 图解法
1.此类问题的特点:合力一定,一个分力的方向一定,另一个分力的方向不断改变,方向的改变引起了两个分力的大小都在变化.
2.此类问题的解法:作动态的矢量三角形,合力所代表的三角形的边不变,一个分力所在边的方向不变,过合力的端点作另一个边(方向变化的边)的平行线,与方向不变的那条边相交便构成三角形,分析三角形的边长变化即可知两个分力的大小变化.
3.利用图解法分析最小力是最简单、最直观、最有效的方法之一.图解法有以下几种情况:
(1)当已知合力F的大小和方向及一个分力F1的方向时,另一个分力F2最小的条件是两个分力互相垂直,如图甲所示,最小值为F2=Fsin α.
(2)当已知合力F的方向及一个分力F1的大小和方向时,另一个分力F2最小的条件是F2与合力F垂直,如图乙所示,最小值为F2=F1sin α.
(3)当已知合力F的大小及一个分力F1的大小时,另一个分力F2最小的条件是分力F1与合力F同方向,最小值为F2=|F-F1|.
培优作业(四)
谢谢观看!
第二章 力
培优课 力的合成与分解
学习目标 重点难点
1.理解分力与合力的关系.
2.理解利用平行四边形定则求合力.
3.会根据平行四边形定则对力的分解进行讨论.
4.掌握力的正交分解法. 1.力的合成与分解是本节学习的重点.
2.对力的分解讨论是本节学习的难点.
一、力的合成
1.分力与合力从效果上看具有什么关系?
提示:等效替代关系
2.力的合成遵循什么法则?
提示:平行四边形定则
3.两个大小一定的力F1、F2,当其夹角θ由0°逐渐增大到180°的过程中其合力大小如何变化?
提示:逐渐减小
4.两个力F1、F2保持两力之间的夹角不变,当其中一个增大时,其合力的大小如何变化?试画图说明.
提示:(1)当0°<θ≤90°时,合力随着其中一个力的增大而增大,如图甲所示.
(2)当90°<θ≤180°时,若F2增大,其合力先变小,后又逐渐增大,如图乙所示.
故合力可能增大、可能不变、也可能减小
5.怎样确定三个力的合力变化范围?
提示:设三个力大小分别是F1、F2、F3.
(1)其合力的最大值为Fmax=F1+F2+F3.
(2)合力的最小值.
①如果三个力中其中任意一个力的大小在另外两个力的合力范围内,即|F1-F2|≤F3≤F1+F2,则合力最小值可以为零.
②如果不满足①中条件,合力的最小值应为最大的力(设为F1)与另外两个较小的力(设为F2、F3)的差,方向与最大的力(F1)同向,即Fmin=F1-(F2+F3).
二、力的分解
1.力的分解遵循什么法则?
提示:平行四边形定则
2.一个力如果不受条件限制可以分解为多少对不同的分力?
提示:一个力分解为两个力,从理论上讲有无数组解.因为以同一条线段为对角线的平行四边形有无穷多个(如图所示)
3.试分析以下情况下力的分解是否具有唯一性?
(1)已知合力和两个分力的方向.
(2)已知合力和一个分力的大小和方向.
(3)已知合力F以及一个分力F1的方向和另一个分力F2的大小时,若F与F1的夹角为α.
提示:
①当Fsin α<F2<F时,有两解,如图甲所示.
②当F2=Fsin α时,有唯一解,如图乙所示.
③当F2<Fsin α时,无解,如图丙所示.
④当F2>F时,有唯一解,如图丁所示.
4.实际问题中,如何分解一个力?
提示:按力的实际效果分解,具体做法是:(1)先根据力的实际作用效果确定两个分力的方向;(2)再根据两个实际分力方向画出平行四边形;(3)最后根据平行四边形和学过的数学知识求出两分力的大小.
三、力的正交分解法
如图所示的三个共点力F1、F2、F3,为求这三个力的合力,试写出用正交分解法求合力的步骤.
提示:具体步骤如下:
(1)建立直角坐标系,以共点力的作用点为坐标原点建立直角坐标系,x轴和y轴的选取原则是使尽量多的力落在坐标轴上;
(2)正交分解各力,即将每一个不在坐标轴上的力分解到坐标轴上,并求出各分力的大小,如图所示;
[解题探究]
(1)如果没有条件限制,F2的最小值是多少?
提示:当F2与F1垂直时,F2的值最小为Fsin 30°
(2)因F2>Fsin 30°,其方向有几种可能?
提示:两种
解析:由平行四边形定则画出力的分解示意图.
答案:AD
如图所示,一小球放置在木板与竖直墙面之间.设球对墙的压力大小为N1,球对木板的压力大小为N2.以木板与墙连接点所形成的水平直线为轴,将木板从图示位置开始缓慢地转到水平位置.不计摩擦,在此过程中( )
A.N1始终减小,N2始终增大
B.N1始终减小,N2始终减小
C.N1先增大后减小,N2始终减小
D.N1先增大后减小,N2先减小后增大
[解题探究]
(1)小球的重力产生了哪两个效果?
提示:对墙和木板产生了压力
(2)当木板与墙的夹角增大时,小球对墙的压力方向变吗?
提示:不变
法二:图解法
木板转动过程中,重力的两个分力中N1的方向不变,N2的方向始终与木板垂直,可作出如图所示的示意图.由图可知N1、N2均减小.
答案:B
[题后总结] 图解法
1.此类问题的特点:合力一定,一个分力的方向一定,另一个分力的方向不断改变,方向的改变引起了两个分力的大小都在变化.
2.此类问题的解法:作动态的矢量三角形,合力所代表的三角形的边不变,一个分力所在边的方向不变,过合力的端点作另一个边(方向变化的边)的平行线,与方向不变的那条边相交便构成三角形,分析三角形的边长变化即可知两个分力的大小变化.
3.利用图解法分析最小力是最简单、最直观、最有效的方法之一.图解法有以下几种情况:
(1)当已知合力F的大小和方向及一个分力F1的方向时,另一个分力F2最小的条件是两个分力互相垂直,如图甲所示,最小值为F2=Fsin α.
(2)当已知合力F的方向及一个分力F1的大小和方向时,另一个分力F2最小的条件是F2与合力F垂直,如图乙所示,最小值为F2=F1sin α.
(3)当已知合力F的大小及一个分力F1的大小时,另一个分力F2最小的条件是分力F1与合力F同方向,最小值为F2=|F-F1|.
培优作业(四)
谢谢观看!
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
