湘教版九年级上册:第4章 锐角三角函数单元测试卷(含解析)
文档属性
| 名称 | 湘教版九年级上册:第4章 锐角三角函数单元测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 388.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 18:23:47 | ||
图片预览




文档简介
第4章 锐角三角函数单元训练卷
一.选择题(共10小题)
1.如图,已知点P(4,3),OP与x轴正半轴的夹角为α,则cosα=( )
A. B. C. D.
2.如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
A.75 sin55° B.75 cos55° C.75 tan55° D.
3.如图,这是某市政道路的交通指示牌.BD的距离为3m,从D点测得指示牌顶端A点和底端C点的仰角分别是60°和45°,则指示牌的高度,即AC的长度是( )
A.3 B.3 C.3﹣3 D.3﹣3
4.小亮为测量如图所示的水湖湖面的宽度BC,他在与水湖处在同一水平面上取一点A,测得湖的一端C在A处的正北方向,另一端B在A处的北偏东60°的方向,并测得A、C间的距离AC=10m,则湖的宽度BC为( )
A.m B.10m C.20m D.20m
5.如图,已知公路l上A、B两点之间的距离为50m,小明要测量点C与河对岸边公路l的距离,测得∠ACB=∠CAB=30°.点C到公路l的距离为( )
A.25m B.m C.25m D.(25+25)m
6.如图,一架长2.5米的梯子AB斜靠在墙上,已知梯子底端B到墙角C的距离为1.5米,设梯子与地面所夹的锐角为α,则cosα的值为( )
A. B. C. D.
7.如图,为了测量河对岸l1上两棵古树A、B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A、B之间的距离为( )
A.50m B.25m C.(50﹣)m D.(50﹣25)m
8.如图,某建筑物AC直立于水平地面,BC=9m,∠B=30°,要建造楼梯,使每级台阶高度不超过20cm,那么此楼梯至少要建( )级(最后一级不足20cm时,按一级计算,≈1.732)
A.27 B.26 C.25 D.24
9.如图,在坡角为30°的山坡FB上有一座信号塔AB,其右侧有一堵防护墙CD,测得BD的长度是30米,当光线AC与水平地面的夹角为53°时,测得信号塔落在防护墙上的影子DE的长为19米,则信号塔AB的高度约为( )
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.73)
A.35.5米 B.37.6米 C.38.6米 D.40.3米
10.如图,在△ABC中,DC平分∠ACB,BD⊥CD于点D,∠ABD=∠A,若BD=1,AC=7,则tan∠CBD的值为( )
A.5 B. C.3 D.
二.填空题(共5小题)
11.如图,在坡度为1:2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,则斜坡上相邻两树间的坡面距离是 m.
12.如图,某幼儿园为了加强安全管理,决定将园内滑梯的倾斜角由45°降为30°,已知点D,B,C在同一水平地面上,且BD的长为2米,则改造后滑梯的长度是 米.(保留根号)
13.如图,大楼底右侧有一障碍物,在障碍物的旁边有一栋小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上).已知AB=40m,DE=10m,则障碍物B,C两点间的距离为 m.(结果保留根号)
14.如图,在△ABC中,AC=2,∠A=15°,∠B=30°,则△ABC的面积为 .
15.如图所示,AB=4,BC=8,AB⊥BC于点B,点D是线段BC上一个动点,且AD⊥DE于点D,,连接CE,则CE长的最小值是 .
三.解答题(共7小题)
16.阳春三月,春暖花开,莲花山风景区游人如织,某摄影爱好者正在用无人机进行航拍.如图,在无人机镜头C处,观测风景区A处的俯角为30°,B处的俯角为45°,已知A,B两点之间的距离为200米,则无人机镜头C处的高度CD为多少?(点A,B,D在同一条直线上,结果保留根号)
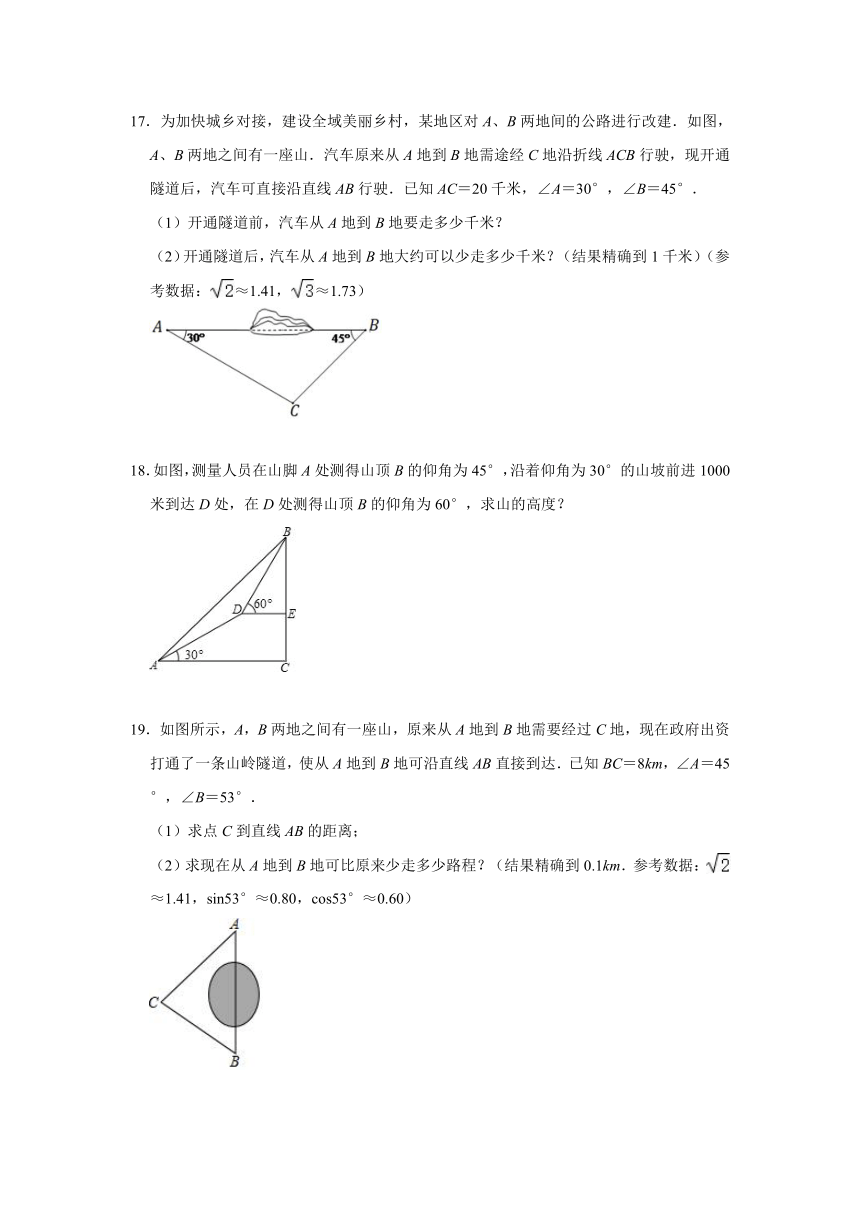
17.为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山.汽车原来从A地到B地需途经C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知AC=20千米,∠A=30°,∠B=45°.
(1)开通隧道前,汽车从A地到B地要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到1千米)(参考数据:≈1.41,≈1.73)
18.如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着仰角为30°的山坡前进1000米到达D处,在D处测得山顶B的仰角为60°,求山的高度?
19.如图所示,A,B两地之间有一座山,原来从A地到B地需要经过C地,现在政府出资打通了一条山岭隧道,使从A地到B地可沿直线AB直接到达.已知BC=8km,∠A=45°,∠B=53°.
(1)求点C到直线AB的距离;
(2)求现在从A地到B地可比原来少走多少路程?(结果精确到0.1km.参考数据:≈1.41,sin53°≈0.80,cos53°≈0.60)
20.为庆祝改革开放40周年,深圳举办了灯光秀,某数学兴趣小组为测量“平安金融中心”AB的高度,他们在地面C处测得另一幢大厦DE的顶部E处的仰角∠ECD=32°.登上大厦DE的顶部E处后,测得“平安中心”AB的顶部A处的仰角为60°,(如图).已知C、D、B三点在同一水平直线上,且CD=400米,DB=200米.
(1)求大厦DE的高度;
(2)求平安金融中心AB的高度;
(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62,≈1.41,≈1.73)
21.如图,小明为测量马路的宽度CD,他从楼AB的楼顶A处分别观测马路的两侧C处和D处,测得C、D两处的俯角∠EAC=70°,∠EAD=52°,已知从楼底B处到C处的距离为BC=40m,且B、C、D三点在同一水平直线上.
(1)求楼的高度AB;
(2)求马路的宽度CD.(结果精确到0.1m)
(参考数据sin52°=0.79,cos52°=0.62,tan52°=1.28,sin70°=0.94,cos70°=0.34,tan70°=2.75)
22.如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,在地面D处测得旗杆顶端B的仰角为30°,在D,C之间选择一点E(D,E,C三点在同一直线上),又测得旗杆顶端B的仰角为60°,且D,E之间的距离为20m,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:≈1.73,≈1.41.
参考答案
一.选择题(共10小题)
1.【解答】解:过P作PN⊥x轴于N,PM⊥y轴于M,则∠PMO=∠PNO=90°,
∵x轴⊥y轴,
∴∠MON=∠PMO=∠PNO=90°,
∴四边形MONP是矩形,
∴PM=ON,PN=OM,
∵P(4,3),
∴ON=PM=4,PN=3,
在Rt△PON中,由勾股定理得
OP=,
∴,
故选:B.
2.【解答】解:根据题意,在Rt△ABC,有AC=75,∠ACB=55°,且tanα=,
则AB=AC×tan55°=75 tan55°,
故选:C.
3.【解答】解:由题意可得:∠CDB=∠DCB=45°,
故BD=BC=3m,
设AC=x,
则tan60°==,
解得:x=3﹣3,
故选:D.
4.【解答】解:根据题意知∠ACB=90°、∠A=60°、AC=10m,
∵tanA=,
∴BC=ACtanA=10tan60°=10(m),
故选:B.
5.【解答】解:如图,过点C作CD⊥直线l于点D,
∵∠ACB=∠CAB=30°,AB=50m,
∴AB=BC=50m,∠CBD=60°,
在Rt△BCD中,∵sin∠CBD=,
∴CD=BCsin∠CBD=50×=25(m),
故选:C.
6.【解答】解:∵在Rt△BAC中,∠ACB=90°,AB=2.5m,BC=1.5m,
∴cosα=cosB===.
故选:A.
7.【解答】解:如图,过点A作AM⊥DC于点M,过点B作BN⊥DC于点N.
则AB=MN,AM=BN.
在直角△ACM,∵∠ACM=45°,AM=50m,
∴CM=AM=50m.
∵在直角△BCN中,∠BCN=∠ACB+∠ACD=60°,BN=50m,
∴CN=(m),
∴MN=CM﹣CN=50﹣(m).
则AB=MN=(50﹣)m.
故选:C.
8.【解答】解:所有台阶高度和为AC的长.
设此楼梯至少要建x阶,可得tan30°==,
所以 x=15≈26(阶).
故选:B.
9.【解答】解:如图,作EG′⊥AB于点G′,BP⊥DE于点P,
则∠DBP=∠BFG′=30°,
∵BD=30,
∴DP=BD=15,BP=BDcos∠DBP=30×=15,
∵DE=19,
∴PE=BG′=DE﹣DP=4,
∵∠AEG′=∠H=53°,
∴∠EAG′=37°
∴AG′==,
则AB=AG′+BG′=+4≈38.6,
故选:C.
10.【解答】解:如图,延长BD交AC于点E.
∵DC平分∠ACB,BD⊥CD于点D,
∴∠CDE=∠CDB=90°,∠DCE=∠DCB.
在△DCE和△DCB中,
,
∴△DCE≌△DCB(SAS).
∴BD=ED=1.
∵∠ABD=∠A,
∴AE=BE=2.
∵AC=7,
∴CE=AC﹣AE=5.
∴CD===2.
∴tan∠CBD===2.
故选:B.
二.填空题(共5小题)
11.【解答】解:∵坡度为1:2,=,且株距为6米,
∴株距:坡面距离=2:,
∴坡面距离=株距×=3(米).
另解:∵CB:AB=1:2,
设CB=x,AB=2x,
∴AC==x,
∴=,
∵AB=6m,
∴AC=×6=3m.
故答案为:3.
12.【解答】解:设AC=x米,
∵∠ABC=45°,
∴BC=AC=x,
∴AB=x,
在Rt△ACD中,tanD=,
∴CD==x,
由题意得,x﹣x=2,
解得,x=+1,
∴AD=2x=(2+2)米,
故答案为:2+2.
13.【解答】解:过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.
则DE=BF=CH=10m,
在Rt△ADF中,AF=AB﹣BF=30m,∠ADF=45°,
∴DF=AF=30m.
在Rt△CDE中,DE=10m,∠DCE=30°,
∴CE===10(m),
∴BC=BE﹣CE=(30﹣10)m.
答:障碍物B,C两点间的距离为(30﹣10)m.
14.【解答】解:过点A作AD⊥BC交BC的延长线于点D,
∵AD⊥BC,
∴∠ADB=90°,
∵∠A=15°,∠B=30°,
∴∠DAC=∠DCA=30°+15°=45°,AB=2AD,
∴AD=CD,
在Rt△ADC中,
AC=2,
∴AD=CD=,
在Rt△ABD中,
BD=,
∴S△ABC=S△ABD﹣S△ADC===﹣1,
故答案为:(﹣1).
15.【解答】解:在BC上截取BQ=3,则CQ=5,Rt△ABQ中,BQ:AB:AQ=3:4:5
∵,
∴在Rt△ADE中,DE:AD:AE=3:4:5,
∴△EAD∽△QAB,
∴,∠QAB=∠EAD,
∴∠BAD=∠QAE,
∴△BAD∽△QAE,
∴∠AQE=90°,
∴∠EQC的角度固定不变,
∴CH为CE的最小值.
过C点作CH⊥EQ交EQ于点H,
∴∠CHQ=∠ABQ=90°,
∵∠AQE=90°,
∴∠CQH=∠QAB,
∴△ABQ∽△QHC,
∵CQ=5,
∴CH=3,
故答案为:3.
三.解答题(共7小题)
16.【解答】解:设CD为x米.
在Rt△ACD中,∠A=30°.
∵,
∴.
在Rt△BCD中,∠CBD=45°,
∴BD=CD=x.
∵AD﹣BD=AB,
∴.
解得x=.
∴高度CD为(100+100)米.
17.【解答】解:(1)作CD⊥AB于D点,
由题意可知:AC=20,∠A=30°,∠B=45°,
∴CD=AC=10,
∵∠B=45°,
∴△BCD是等腰直角三角形,
∴BD=CD=10,
∴BC=CD=10,
∴AC+BC=20+10,
即开通隧道前,汽车从A地到B地要走(20+10)千米;
(2)由(1)知CD=10,
∵CD⊥AB,∠B=45°,
∴△BCD是等腰直角三角形,
∴CD=BD=10,
∵AD=AC=10,
∴AB=10+10≈17.3+10=27.3,
∵AC+BC=20+10≈20+14.1=34.1
∴34.1﹣27.3=6.8≈7,
答:开通隧道后,汽车从A地到B地大约可以少走7千米.
18.【解答】解:∵∠BAC=45°,∠DAC=30°,
∴∠BAD=15°,
∵∠BDE=60°,∠BED=90°,
∴∠DBE=30°,
∵∠ABC=45°,
∴∠ABD=15°,
∴∠ABD=∠DAB,
∴AD=BD=1000,
过点D作DF⊥AC,
∵AC⊥BC,DE⊥AC,DE⊥BC,
∴∠DFC=∠ACB=∠DEC=90°
∴四边形DFCE是矩形
∴DF=CE
在直角三角ADF中,∵∠DAF=30°,
∴DF=AD=500,
∴EC=500,BE=1000×sin60°=500.
∴BC=500+500米.
19.【解答】解:(1)如图所示,作CD⊥AB于点D,
由题意知,∠B=53°、∠A=45°、BC=8,
则CD=BCsinB=8sin53°≈6.4;
(2)∵BD=BCcos53°≈4.8,AD=CD=6.4,
∴AB=AD+BD=11.2,
又∵AC=CD≈9.0,
∴AC+BC=9.0+8=17.0,
则17.0﹣11.2=5.8(km),
答:现在从A地到B地可比原来少走5.8km路程.
20.【解答】解:(1)∵在Rt△DCE中,∠CDE=90°,∠ECD=32°,CD=400米,
∴DE=CD tan∠ECD≈400×0.62=248(米).
故大厦DE的高度约为248米;
(2)如图,作EF⊥AB于F.
由题意,得EF=DB=200米,BF=DE=248米,∠AEF=60°.
∵在Rt△AFE中,∠AFE=90°,
∴AF=EF tan∠AEF≈200×1.73=346(米),
∴AB=BF+AF=248+346=594(米).
故平安金融中心AB的高度约为594米.
21.【解答】解:
(1)由已知得,∠ACB=∠EAC=70°,
在Rt△ABC中,∵tan∠ACB=,
∴AB=BCtan∠ACB=40tan70°=40×2.75=110.0m,
答:楼的高度AB为110.0m.
(2)由已知得,∠ADB=∠EAD=52°,
在Rt△ABD中,∵tan∠ADB=,
∴BD==85.94m,
∴CD=BD﹣BC=85.94﹣40≈45.9m,
答:马路的宽CD约为45.9m.
22.【解答】解:∵∠BEC=60°,∠BDE=30°,
∴∠DBE=60°﹣30°=30°,
∴BE=DE=20m,
在Rt△BEC中,
BC=BE sin60°=20×=10≈17.3(m),
∴AB=BC﹣AC=17.3﹣12=5.3(m),
答:旗杆AB的高度为5.3m.
一.选择题(共10小题)
1.如图,已知点P(4,3),OP与x轴正半轴的夹角为α,则cosα=( )
A. B. C. D.
2.如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
A.75 sin55° B.75 cos55° C.75 tan55° D.
3.如图,这是某市政道路的交通指示牌.BD的距离为3m,从D点测得指示牌顶端A点和底端C点的仰角分别是60°和45°,则指示牌的高度,即AC的长度是( )
A.3 B.3 C.3﹣3 D.3﹣3
4.小亮为测量如图所示的水湖湖面的宽度BC,他在与水湖处在同一水平面上取一点A,测得湖的一端C在A处的正北方向,另一端B在A处的北偏东60°的方向,并测得A、C间的距离AC=10m,则湖的宽度BC为( )
A.m B.10m C.20m D.20m
5.如图,已知公路l上A、B两点之间的距离为50m,小明要测量点C与河对岸边公路l的距离,测得∠ACB=∠CAB=30°.点C到公路l的距离为( )
A.25m B.m C.25m D.(25+25)m
6.如图,一架长2.5米的梯子AB斜靠在墙上,已知梯子底端B到墙角C的距离为1.5米,设梯子与地面所夹的锐角为α,则cosα的值为( )
A. B. C. D.
7.如图,为了测量河对岸l1上两棵古树A、B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A、B之间的距离为( )
A.50m B.25m C.(50﹣)m D.(50﹣25)m
8.如图,某建筑物AC直立于水平地面,BC=9m,∠B=30°,要建造楼梯,使每级台阶高度不超过20cm,那么此楼梯至少要建( )级(最后一级不足20cm时,按一级计算,≈1.732)
A.27 B.26 C.25 D.24
9.如图,在坡角为30°的山坡FB上有一座信号塔AB,其右侧有一堵防护墙CD,测得BD的长度是30米,当光线AC与水平地面的夹角为53°时,测得信号塔落在防护墙上的影子DE的长为19米,则信号塔AB的高度约为( )
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.73)
A.35.5米 B.37.6米 C.38.6米 D.40.3米
10.如图,在△ABC中,DC平分∠ACB,BD⊥CD于点D,∠ABD=∠A,若BD=1,AC=7,则tan∠CBD的值为( )
A.5 B. C.3 D.
二.填空题(共5小题)
11.如图,在坡度为1:2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,则斜坡上相邻两树间的坡面距离是 m.
12.如图,某幼儿园为了加强安全管理,决定将园内滑梯的倾斜角由45°降为30°,已知点D,B,C在同一水平地面上,且BD的长为2米,则改造后滑梯的长度是 米.(保留根号)
13.如图,大楼底右侧有一障碍物,在障碍物的旁边有一栋小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上).已知AB=40m,DE=10m,则障碍物B,C两点间的距离为 m.(结果保留根号)
14.如图,在△ABC中,AC=2,∠A=15°,∠B=30°,则△ABC的面积为 .
15.如图所示,AB=4,BC=8,AB⊥BC于点B,点D是线段BC上一个动点,且AD⊥DE于点D,,连接CE,则CE长的最小值是 .
三.解答题(共7小题)
16.阳春三月,春暖花开,莲花山风景区游人如织,某摄影爱好者正在用无人机进行航拍.如图,在无人机镜头C处,观测风景区A处的俯角为30°,B处的俯角为45°,已知A,B两点之间的距离为200米,则无人机镜头C处的高度CD为多少?(点A,B,D在同一条直线上,结果保留根号)
17.为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山.汽车原来从A地到B地需途经C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知AC=20千米,∠A=30°,∠B=45°.
(1)开通隧道前,汽车从A地到B地要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到1千米)(参考数据:≈1.41,≈1.73)
18.如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着仰角为30°的山坡前进1000米到达D处,在D处测得山顶B的仰角为60°,求山的高度?
19.如图所示,A,B两地之间有一座山,原来从A地到B地需要经过C地,现在政府出资打通了一条山岭隧道,使从A地到B地可沿直线AB直接到达.已知BC=8km,∠A=45°,∠B=53°.
(1)求点C到直线AB的距离;
(2)求现在从A地到B地可比原来少走多少路程?(结果精确到0.1km.参考数据:≈1.41,sin53°≈0.80,cos53°≈0.60)
20.为庆祝改革开放40周年,深圳举办了灯光秀,某数学兴趣小组为测量“平安金融中心”AB的高度,他们在地面C处测得另一幢大厦DE的顶部E处的仰角∠ECD=32°.登上大厦DE的顶部E处后,测得“平安中心”AB的顶部A处的仰角为60°,(如图).已知C、D、B三点在同一水平直线上,且CD=400米,DB=200米.
(1)求大厦DE的高度;
(2)求平安金融中心AB的高度;
(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62,≈1.41,≈1.73)
21.如图,小明为测量马路的宽度CD,他从楼AB的楼顶A处分别观测马路的两侧C处和D处,测得C、D两处的俯角∠EAC=70°,∠EAD=52°,已知从楼底B处到C处的距离为BC=40m,且B、C、D三点在同一水平直线上.
(1)求楼的高度AB;
(2)求马路的宽度CD.(结果精确到0.1m)
(参考数据sin52°=0.79,cos52°=0.62,tan52°=1.28,sin70°=0.94,cos70°=0.34,tan70°=2.75)
22.如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,在地面D处测得旗杆顶端B的仰角为30°,在D,C之间选择一点E(D,E,C三点在同一直线上),又测得旗杆顶端B的仰角为60°,且D,E之间的距离为20m,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:≈1.73,≈1.41.
参考答案
一.选择题(共10小题)
1.【解答】解:过P作PN⊥x轴于N,PM⊥y轴于M,则∠PMO=∠PNO=90°,
∵x轴⊥y轴,
∴∠MON=∠PMO=∠PNO=90°,
∴四边形MONP是矩形,
∴PM=ON,PN=OM,
∵P(4,3),
∴ON=PM=4,PN=3,
在Rt△PON中,由勾股定理得
OP=,
∴,
故选:B.
2.【解答】解:根据题意,在Rt△ABC,有AC=75,∠ACB=55°,且tanα=,
则AB=AC×tan55°=75 tan55°,
故选:C.
3.【解答】解:由题意可得:∠CDB=∠DCB=45°,
故BD=BC=3m,
设AC=x,
则tan60°==,
解得:x=3﹣3,
故选:D.
4.【解答】解:根据题意知∠ACB=90°、∠A=60°、AC=10m,
∵tanA=,
∴BC=ACtanA=10tan60°=10(m),
故选:B.
5.【解答】解:如图,过点C作CD⊥直线l于点D,
∵∠ACB=∠CAB=30°,AB=50m,
∴AB=BC=50m,∠CBD=60°,
在Rt△BCD中,∵sin∠CBD=,
∴CD=BCsin∠CBD=50×=25(m),
故选:C.
6.【解答】解:∵在Rt△BAC中,∠ACB=90°,AB=2.5m,BC=1.5m,
∴cosα=cosB===.
故选:A.
7.【解答】解:如图,过点A作AM⊥DC于点M,过点B作BN⊥DC于点N.
则AB=MN,AM=BN.
在直角△ACM,∵∠ACM=45°,AM=50m,
∴CM=AM=50m.
∵在直角△BCN中,∠BCN=∠ACB+∠ACD=60°,BN=50m,
∴CN=(m),
∴MN=CM﹣CN=50﹣(m).
则AB=MN=(50﹣)m.
故选:C.
8.【解答】解:所有台阶高度和为AC的长.
设此楼梯至少要建x阶,可得tan30°==,
所以 x=15≈26(阶).
故选:B.
9.【解答】解:如图,作EG′⊥AB于点G′,BP⊥DE于点P,
则∠DBP=∠BFG′=30°,
∵BD=30,
∴DP=BD=15,BP=BDcos∠DBP=30×=15,
∵DE=19,
∴PE=BG′=DE﹣DP=4,
∵∠AEG′=∠H=53°,
∴∠EAG′=37°
∴AG′==,
则AB=AG′+BG′=+4≈38.6,
故选:C.
10.【解答】解:如图,延长BD交AC于点E.
∵DC平分∠ACB,BD⊥CD于点D,
∴∠CDE=∠CDB=90°,∠DCE=∠DCB.
在△DCE和△DCB中,
,
∴△DCE≌△DCB(SAS).
∴BD=ED=1.
∵∠ABD=∠A,
∴AE=BE=2.
∵AC=7,
∴CE=AC﹣AE=5.
∴CD===2.
∴tan∠CBD===2.
故选:B.
二.填空题(共5小题)
11.【解答】解:∵坡度为1:2,=,且株距为6米,
∴株距:坡面距离=2:,
∴坡面距离=株距×=3(米).
另解:∵CB:AB=1:2,
设CB=x,AB=2x,
∴AC==x,
∴=,
∵AB=6m,
∴AC=×6=3m.
故答案为:3.
12.【解答】解:设AC=x米,
∵∠ABC=45°,
∴BC=AC=x,
∴AB=x,
在Rt△ACD中,tanD=,
∴CD==x,
由题意得,x﹣x=2,
解得,x=+1,
∴AD=2x=(2+2)米,
故答案为:2+2.
13.【解答】解:过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.
则DE=BF=CH=10m,
在Rt△ADF中,AF=AB﹣BF=30m,∠ADF=45°,
∴DF=AF=30m.
在Rt△CDE中,DE=10m,∠DCE=30°,
∴CE===10(m),
∴BC=BE﹣CE=(30﹣10)m.
答:障碍物B,C两点间的距离为(30﹣10)m.
14.【解答】解:过点A作AD⊥BC交BC的延长线于点D,
∵AD⊥BC,
∴∠ADB=90°,
∵∠A=15°,∠B=30°,
∴∠DAC=∠DCA=30°+15°=45°,AB=2AD,
∴AD=CD,
在Rt△ADC中,
AC=2,
∴AD=CD=,
在Rt△ABD中,
BD=,
∴S△ABC=S△ABD﹣S△ADC===﹣1,
故答案为:(﹣1).
15.【解答】解:在BC上截取BQ=3,则CQ=5,Rt△ABQ中,BQ:AB:AQ=3:4:5
∵,
∴在Rt△ADE中,DE:AD:AE=3:4:5,
∴△EAD∽△QAB,
∴,∠QAB=∠EAD,
∴∠BAD=∠QAE,
∴△BAD∽△QAE,
∴∠AQE=90°,
∴∠EQC的角度固定不变,
∴CH为CE的最小值.
过C点作CH⊥EQ交EQ于点H,
∴∠CHQ=∠ABQ=90°,
∵∠AQE=90°,
∴∠CQH=∠QAB,
∴△ABQ∽△QHC,
∵CQ=5,
∴CH=3,
故答案为:3.
三.解答题(共7小题)
16.【解答】解:设CD为x米.
在Rt△ACD中,∠A=30°.
∵,
∴.
在Rt△BCD中,∠CBD=45°,
∴BD=CD=x.
∵AD﹣BD=AB,
∴.
解得x=.
∴高度CD为(100+100)米.
17.【解答】解:(1)作CD⊥AB于D点,
由题意可知:AC=20,∠A=30°,∠B=45°,
∴CD=AC=10,
∵∠B=45°,
∴△BCD是等腰直角三角形,
∴BD=CD=10,
∴BC=CD=10,
∴AC+BC=20+10,
即开通隧道前,汽车从A地到B地要走(20+10)千米;
(2)由(1)知CD=10,
∵CD⊥AB,∠B=45°,
∴△BCD是等腰直角三角形,
∴CD=BD=10,
∵AD=AC=10,
∴AB=10+10≈17.3+10=27.3,
∵AC+BC=20+10≈20+14.1=34.1
∴34.1﹣27.3=6.8≈7,
答:开通隧道后,汽车从A地到B地大约可以少走7千米.
18.【解答】解:∵∠BAC=45°,∠DAC=30°,
∴∠BAD=15°,
∵∠BDE=60°,∠BED=90°,
∴∠DBE=30°,
∵∠ABC=45°,
∴∠ABD=15°,
∴∠ABD=∠DAB,
∴AD=BD=1000,
过点D作DF⊥AC,
∵AC⊥BC,DE⊥AC,DE⊥BC,
∴∠DFC=∠ACB=∠DEC=90°
∴四边形DFCE是矩形
∴DF=CE
在直角三角ADF中,∵∠DAF=30°,
∴DF=AD=500,
∴EC=500,BE=1000×sin60°=500.
∴BC=500+500米.
19.【解答】解:(1)如图所示,作CD⊥AB于点D,
由题意知,∠B=53°、∠A=45°、BC=8,
则CD=BCsinB=8sin53°≈6.4;
(2)∵BD=BCcos53°≈4.8,AD=CD=6.4,
∴AB=AD+BD=11.2,
又∵AC=CD≈9.0,
∴AC+BC=9.0+8=17.0,
则17.0﹣11.2=5.8(km),
答:现在从A地到B地可比原来少走5.8km路程.
20.【解答】解:(1)∵在Rt△DCE中,∠CDE=90°,∠ECD=32°,CD=400米,
∴DE=CD tan∠ECD≈400×0.62=248(米).
故大厦DE的高度约为248米;
(2)如图,作EF⊥AB于F.
由题意,得EF=DB=200米,BF=DE=248米,∠AEF=60°.
∵在Rt△AFE中,∠AFE=90°,
∴AF=EF tan∠AEF≈200×1.73=346(米),
∴AB=BF+AF=248+346=594(米).
故平安金融中心AB的高度约为594米.
21.【解答】解:
(1)由已知得,∠ACB=∠EAC=70°,
在Rt△ABC中,∵tan∠ACB=,
∴AB=BCtan∠ACB=40tan70°=40×2.75=110.0m,
答:楼的高度AB为110.0m.
(2)由已知得,∠ADB=∠EAD=52°,
在Rt△ABD中,∵tan∠ADB=,
∴BD==85.94m,
∴CD=BD﹣BC=85.94﹣40≈45.9m,
答:马路的宽CD约为45.9m.
22.【解答】解:∵∠BEC=60°,∠BDE=30°,
∴∠DBE=60°﹣30°=30°,
∴BE=DE=20m,
在Rt△BEC中,
BC=BE sin60°=20×=10≈17.3(m),
∴AB=BC﹣AC=17.3﹣12=5.3(m),
答:旗杆AB的高度为5.3m.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
