认识三角形.[下学期]

课件28张PPT。 认识三角形(2)
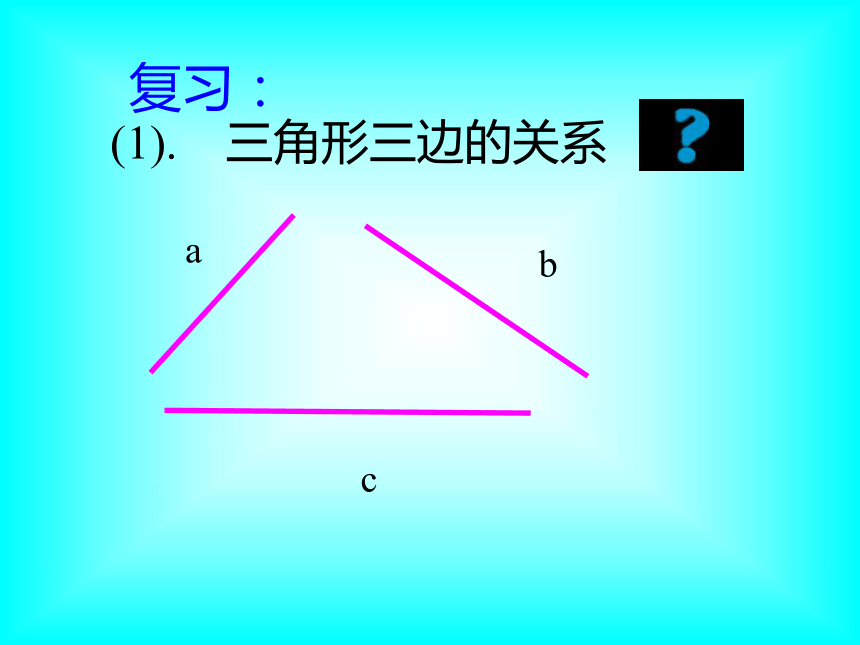
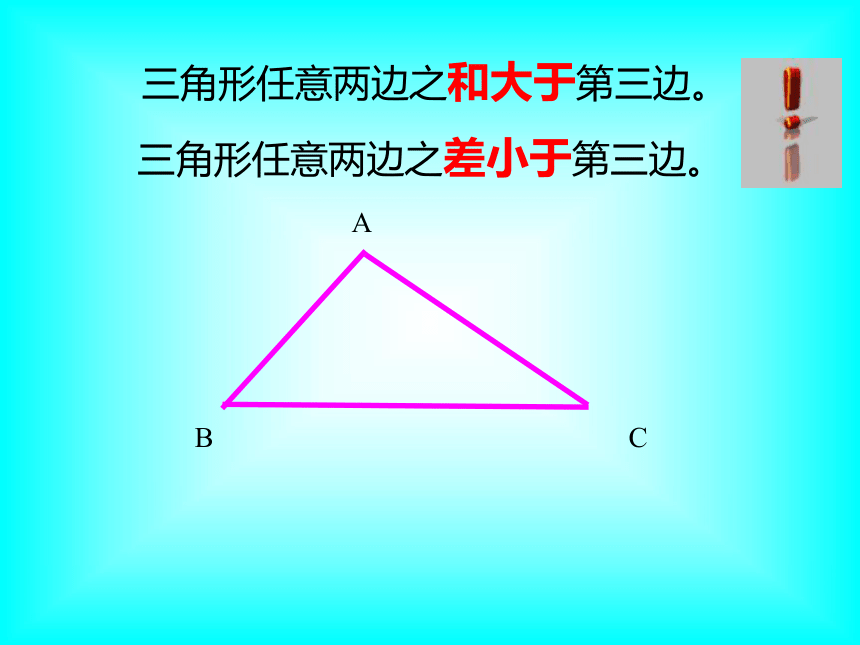
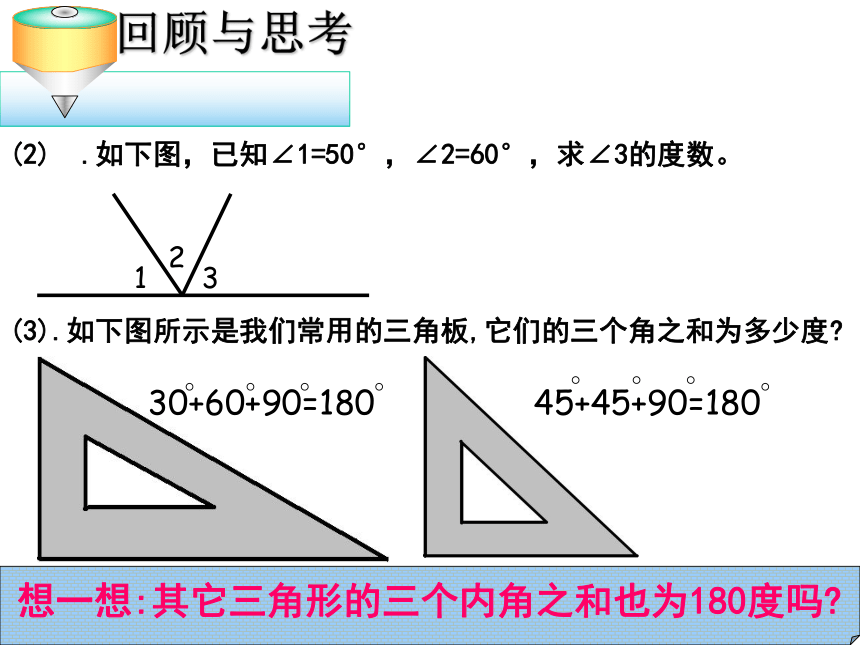
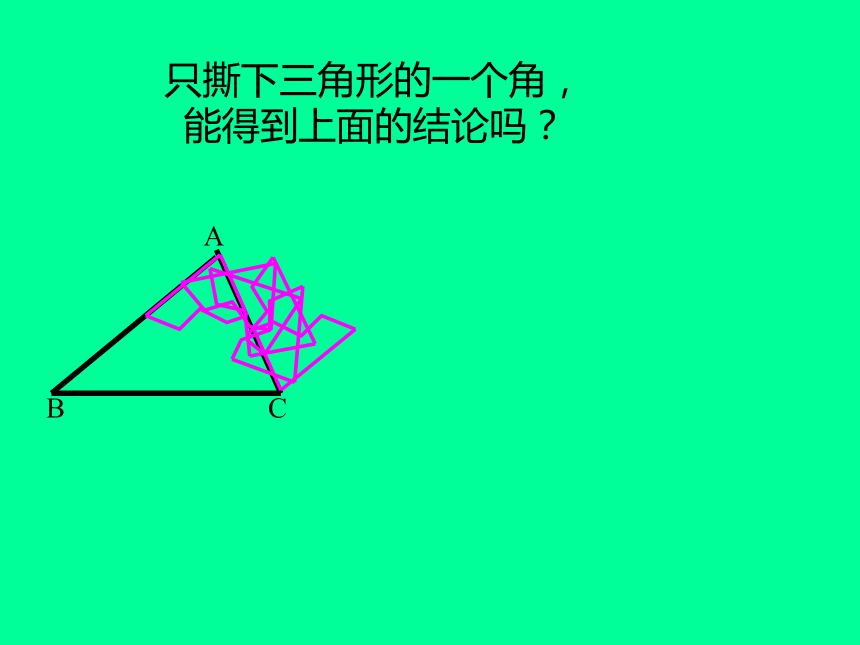
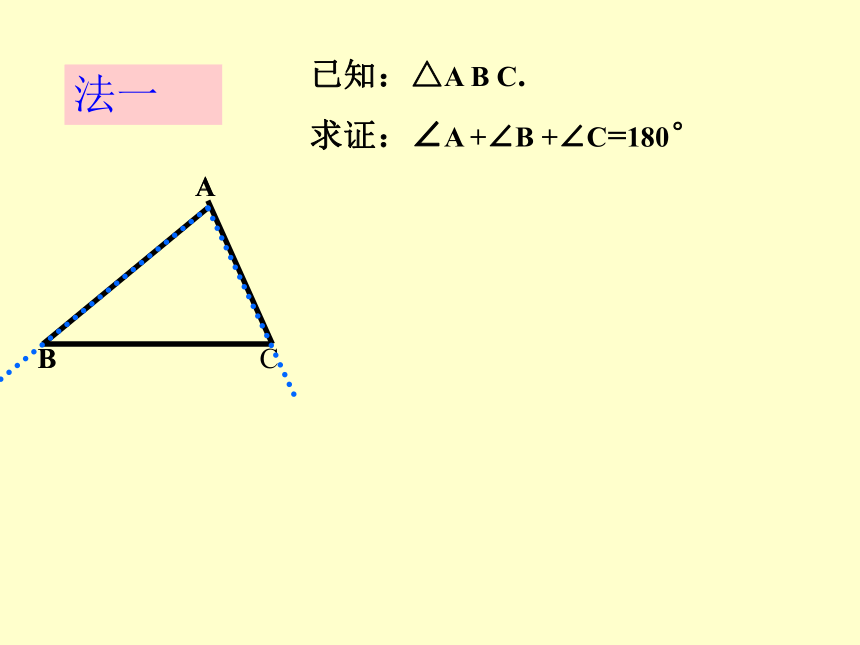
(1). 三角形三边的关系复习：三角形任意两边之和大于第三边。三角形任意两边之差小于第三边。(2) .如下图，已知∠1=50°，∠2=60°，求∠3的度数。(3).如下图所示是我们常用的三角板,它们的三个角之和为多少度?想一想:其它三角形的三个内角之和也为180度吗?三角形的三个内角有什么关系小学里，用什么方法得到三角形内角和的结论的？请同学们动手验证一下！只撕下三角形的一个角，能得到上面的结论吗？法一AB已知：△A B C.
求证：∠A +∠B +∠C=180°法一已知：△A B C.
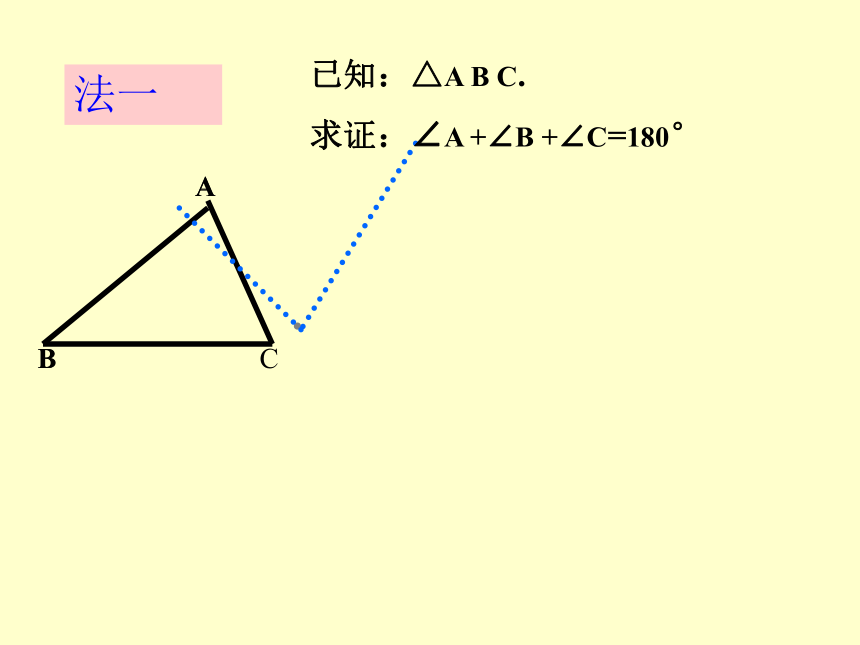
求证：∠A +∠B +∠C=180°AB法一已知：△A B C.
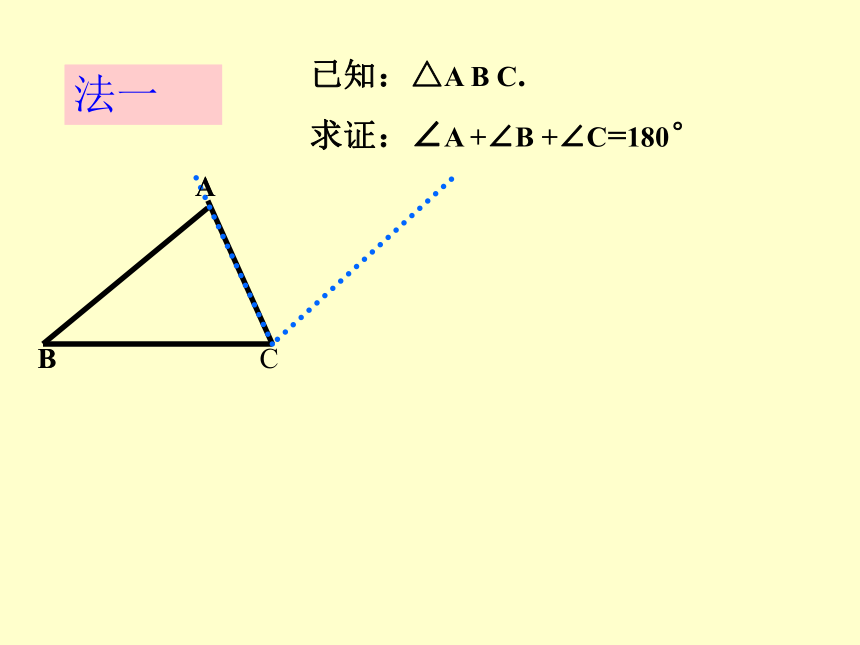
求证：∠A +∠B +∠C=180°ABED证法一法一已知：△A B C.
求证：∠A +∠B +∠C=180° 在△A B C的外部以C A 为边作∠A C E =∠A. 延长B C至D 。AABC三角形三个内角的和等于180o。平移一个角，也能得到上面的结论吗？法二已知：△A B C.
求证：∠A +∠B +∠C =180°D E 证明：延长B C至D ，过C作C E∥B A. AB三角形三个内角的和等于180o。ABC法三过点A作BC的平行线EF “你还有没有其它添辅助线的方法”，课后想一想！三角形三个内角的和等于180o。ABC2.在△ABC中， ∠ A= 80°, ∠B= ∠C , 求∠C的度数?试一试80°（１）下图中小明所拿三角形被遮住的两个内角是什么角？小颖的
　　　呢？试着说明理由．(2)下图中三角形被遮住的两个内角可能是什么角?将所
得结果与(1)的结果进行比较.锐角三角形直角三角形钝角三角形（三个内角都是锐角。）（有一个内角是直角。）（有一个内角是钝角。）直角三角形的两个锐角互余。“直角三角形ABC”用符号“Rt△ABC”表示。斜边D
练习：122页第2题锐角三角形直角三角形钝角三角形⑦②①③④⑤⑥①②③④⑤⑥⑦1.三角形内角和定理:三角形的内角和等于180°。即：△ABC中， ∠A +∠B +∠C=180 °2.推论：直角三角形的两个锐角互余。即： R t △A B C 中，∠C =90°， 则∠A +∠B=90 °。3.三角形按角分类可分为：
锐角三角形（三个内角都是锐角）
直角三角形（有一个角是直角）
钝角三角形（有一个角是钝角）挑战题　１.已知三角形三个内角的度数之比１:３:５，求这个三角形各个角的度数?解：设这个三角形的三个内角分别为x,3x,5x,则
　x+3x+5x=180 °
　解得:x= 20 °
　所以这个三角形的三个内角分别是
　　　　20 °， ６0 °，１０0 °２.如图线段DG ,EM ,FN两两相交于B ,C ,A三点　则 ∠D+ ∠E + ∠F+∠G+∠M+∠N的度数是________。３６0 °３.将一个三角形纸片剪一刀分成两个三角形，能使两个三角形都是（１）锐角三角形,（２）直角三角形,（３）钝角三角形,　若能剪，用纸片剪下来贴出来，若不能简要说明理由．　谢谢，再见！