有理数

课件15张PPT。§1.2.1 有理数学习目的：1，理解什么是有理数。
2，有理数的两种分类方法。
3，整数、分数与正负数之间的联系。
4，观察一列数字，找出它们的规律。学习重点：有理数的两种分类方法。学习难点：整数、分数与正负数之间的联系。复习与回顾：上一节课我们讲了些什么内容？1，正数和负数。
2，0既不是正数，也不是负数。
3，正数与负数通常用来表示具有相反意义的
量。
4，“0”所表示的意思。
5，在生产中，通常用正负数来表示允许误差；温故知新：1，(2005年 吉林)如果自行车车条的长度比标准长度长2mm，记作+2mm，那么比标准长度短1.5mm，应记为________。-1.5mm2,粮食每袋标准重量是50千克，先测得甲、乙、丙三袋粮食重量如下：52千克，49千克，49.8千克，如果超重部分用正数表示，请用正数和负数记录甲、乙、丙三袋粮食的超重数和不足数；3，国际乒联在正式比赛中采用打球，对大球的直径有严格的标准，现有5个乒乓球，测量它们的直径，超过标准的毫米数记为正数，不足的记为负数，测量结果如下：
A.-0.1mm B.-0.2mm C.+0.25mm D.-0.05mm E.+0.15mm
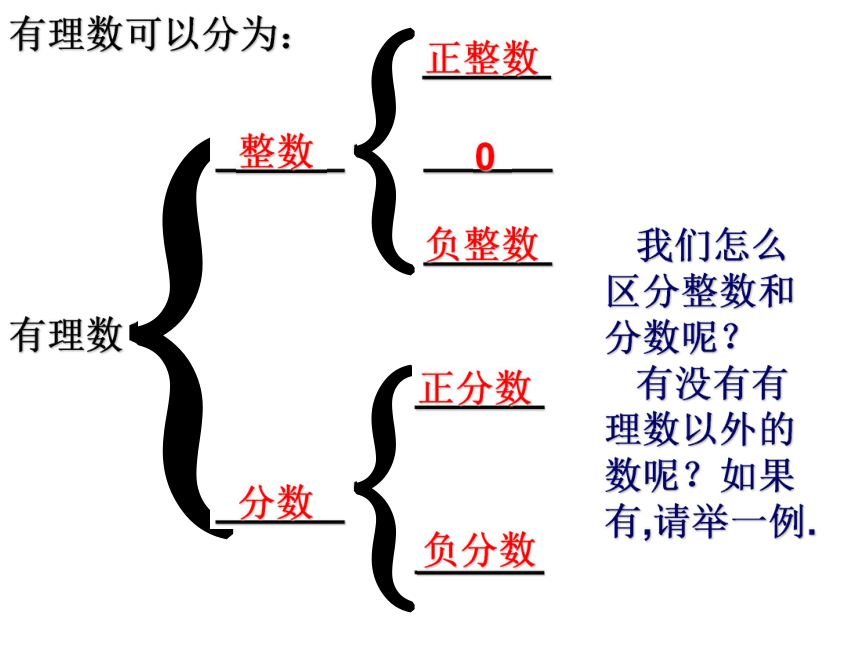
你认为应该选哪一个乒乓球用于比赛呢？为什么？我们学过的数有什么？正整数：如1，2，3，…；零：0；负整数：如－1，－2，－3，…；正分数：如负分数：如1，正整数、0和负整数合称整数；2，正分数、负分数合称分数；3，整数和分数合称有理数；有理数可以分为：有理数______________________________整数分数正整数0负整数正分数负分数 我们怎么区分整数和分数呢？
有没有有理数以外的数呢？如果有,请举一例.有理数分类的几点注意：1，如 能约分成整数的数_____(填“能”或“不能”)算做分数；2，两个整数的比（如 等）、有限小数（如0.2，－3.14等）、无限循环小数
（如 等）都是分数；但无限不循环小数（如 等）不是分数；不能3，无限不循环小数不是有理数；(无理数)4，整数中除了正整数和负整数，还有_____.0有理数还有其他的分类方法吗？有理数__________________有理数还可以分为：________________________正有理数0负有理数正整数正分数负整数负分数注意：正数和正有理数是不同的，例如：
就是正数，但不是正有理数；
正数和正有理数有什么区别呢？例1：把下列各数填在相应的集合中：正数集合：{ }；
负数集合：{ }；
分数集合：{ }；
整数集合：{ }；
非负数集合：{ }；
有理数集合：{ }；注意：1，像 这种可以先化简成整数的数是
整数不是分数；2，非负整数集合包括正整数和0，也称为自然数集合.例2，下列说法正确的是 （ ）
A.非负有理数就是正有理数
B. 0仅表示没有，是有理数
C.正整数和负整数统称为整数
D.整数和分数统称为有理数D例3，最小的正整数是______，最大的负整数是_____,所有大于-4的负整数有_________，不大于3的非负整数有____________。1-1-1,-2,-30,1,2,3例4，下列说法正确的是（ ）
①1是最小的正有理数； ②-1是最大的负有理数；
③0是最小的非负有理数；④0是最大的非正有理数；
A.①② B.②③
C.③④ D.①④C例5，将下列各数分别填入相应的集合中；正整数集合负分数集合正有理数集合非正数集合例6 （1）既是分数又是负数的数是_______；
（2）既是非负数又是整数的数是_______；
（3）非负整数又称为________；
（4）非负数包括________和_______；
（5）非正数包括________和_______；非负整数负分数自然数例7 下图中的两个圆分别表示正数集合和分数集合，请你在每个圆中及它们重叠的部分各填入3个数；正数集合分数集合正数0负数0例8 观察下列各组数，请找出它们的规律，并在横线上填上相应的数字；6810-1014-16这节课我们学到了什么？小结：1，什么是有理数？
2，有理数的分类：
（1）按整数与分数划分；
（2）按正有理数，0，负有理数划分；3，如何区分整数和分数？4，如何理解非正数和非负数？5，整数和分数，正数和负数之间有什么关系？6，学会观察一列数字之间的规律；进步往往从归纳反思开始！乘风破浪会有时，
直挂云帆济沧海！
谢谢大家，再见！