2022-2023学年人教版数学八年级上册13.3实验与探究 三角形中边与角之间的不等关系 课件(共20张PPT)
文档属性
| 名称 | 2022-2023学年人教版数学八年级上册13.3实验与探究 三角形中边与角之间的不等关系 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 817.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-16 15:53:30 | ||
图片预览




文档简介
(共20张PPT)
三角形中边与角之间的不等关系
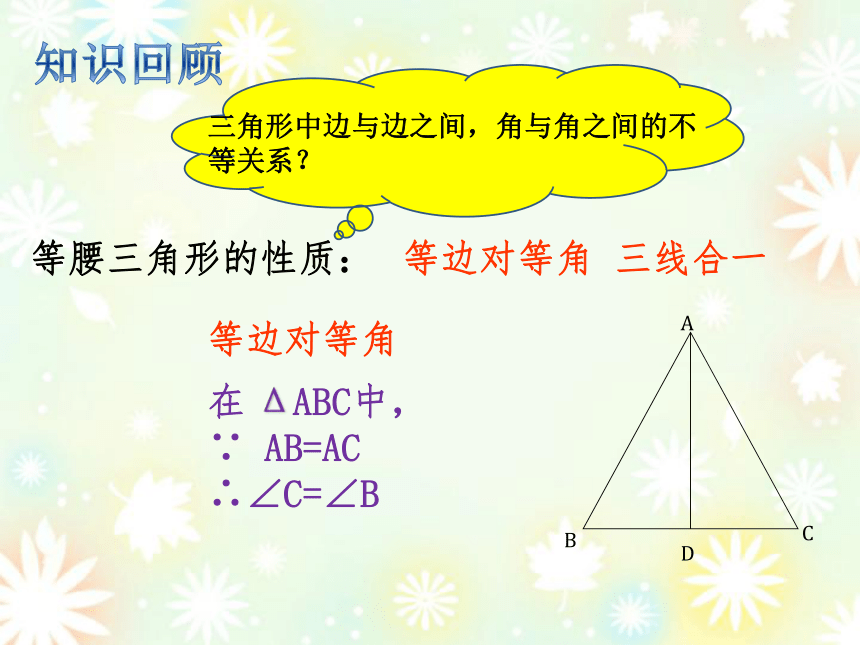
知识回顾
等腰三角形的性质:
等边对等角
等边对等角
A
B
C
D
三线合一
三角形中边与边之间,角与角之间的不等关系?
在 ΔABC中,
∵ AB=AC
∴∠C=∠B
在一个三角形中,如果两条边不相等,那么它们所对的角是否相等呢?
思考
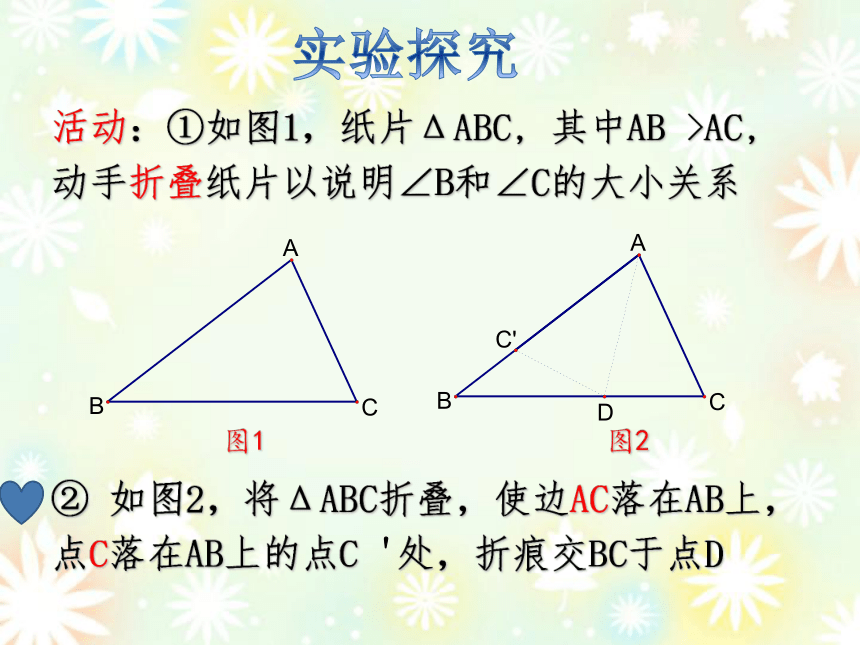
实验探究
图1
图2
② 如图2,将ΔABC折叠,使边AC落在AB上,
点C落在AB上的点C '处,折痕交BC于点D
活动:①如图1,纸片ΔABC, 其中AB >AC,
动手折叠纸片以说明∠B和∠C的大小关系
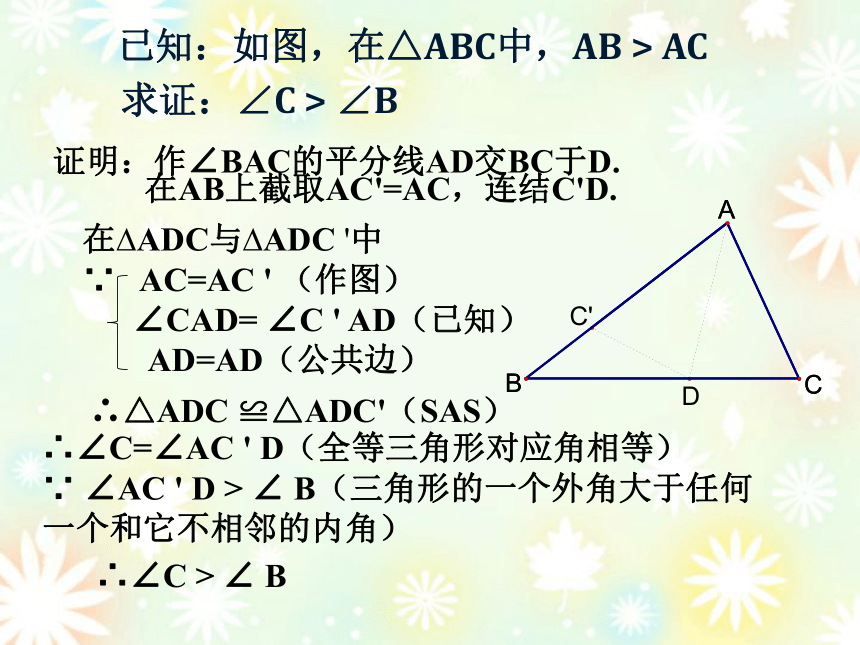
已知:如图,在△ABC中,AB > AC
求证:∠C > ∠B
证明:作∠BAC的平分线AD交BC于D.
在AB上截取AC'=AC,连结C'D.
∴△ADC ≌△ADC'(SAS)
∴∠C=∠AC ' D(全等三角形对应角相等)
∵ ∠AC ' D > ∠ B(三角形的一个外角大于任何一个和它不相邻的内角)
在 ADC与 ADC '中
∵ AC=AC ' (作图)
∠CAD= ∠C ' AD(已知)
AD=AD(公共边)
∴∠C > ∠ B
D
E
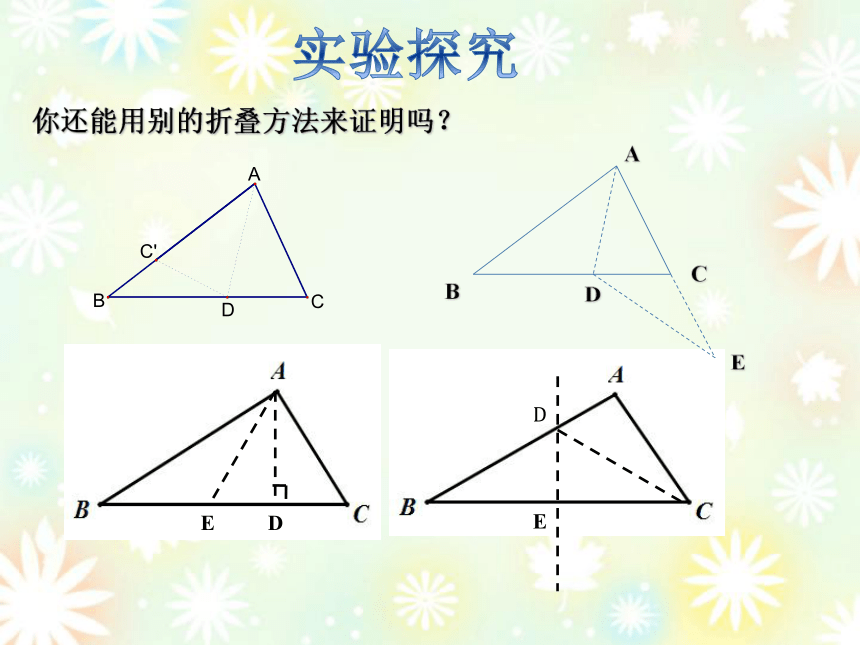
实验探究
你还能用别的折叠方法来证明吗?
E
D
A
B
C
D
E
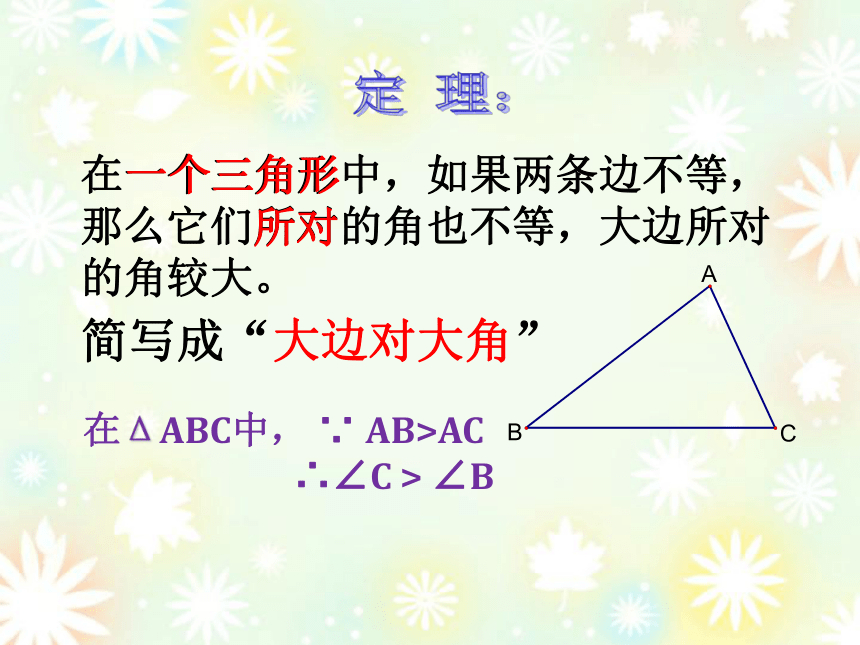
定 理:
在一个三角形中,如果两条边不等,那么它们所对的角也不等,大边所对的角较大。
一个三角形
所对
简写成“大边对大角”
在ΔABC中, ∵ AB>AC
∴∠C > ∠B
1、在ΔABC中,已知BC > AB > AC,那么∠A,∠B,∠C的大小关系为_____________
∠A>∠C>∠B
知识运用
2、如果一个三角形中最大的边所对的角是锐角,这个三角形一定是锐角三角形吗?为什么?
知识运用
如图,在四边形ABCD中,四条
边不等,AD边最大,BC边最小
求证:∠B >∠D
牛刀小试
请谈谈你的收获
小结:
三角形中的边与角之间的不等关系
简写成:大边对大角
在⊿ABC中, ∵ AB>AC
∴∠C > ∠B
定理:在一个三角形中,如果两条边不等,那么它们所对的角也不等,大边所对的角较大。
在解决问题时,我们可以将新问题转化到我们已知的、熟悉的定理,用已有的知识解决新问题.利用轴对称的性质,可以把研究边与角之间的不等问题,转化为外角的问题,这种转化的思想是研究几何问题时常用的方法.
3、如图,在三角形△ABC中,AB>AC,P为AC延长线上一点,PD⊥BC,分别交BC、BA的延长线于D、E。判断∠E和∠P的大小关系并证明。
课后训练
1、整理做法:选出两种你喜欢的作法完成证明.
2、类比今天探究“大边对大角”的活动过程,请你探究命题“大角对大边”.
悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,去发现.去总结
下课了!
再见
结束寄语
E
D
我们的方法
D
“大边对大角”有没有逆定理?
逆命题:“大角对大边”
已知:如图,在△ABC中,∠C>∠B
求证: AC > AB
思考
已知:如图,在△ABC中,∠C > ∠B
求证:AB > AC
证明:作BC的垂直平分线MN,分别交AB、BC
于M、N,连结MC.
∴MB = MC(线段垂直平分线上的点和线段两个
端点的距离相等)
∴MA+MB > AC(等量代换)
∵MA + MC > AC(三角形的任何
两边的和大于第三边)
即AB > AC
∵MN垂直平分BC(已知)
定理及逆定理:
定理:在一个三角形中,如果两条边不等,那么它们所对的角也不等,大边所对的角较大。
一个三角形
所对
简写成“大边对大角”
逆定理:在一个三角形中,如果两个角不等,那么它们所对的边也不等,大角所对的边较大。
简写成“大角对大边”
一个三角形
所对
2、如图,AD是△ABC中∠BAC的
平分线,E在AB上,且EB = EC,
∠ACE >∠ECB,AD,EC相交
于O
求证:DC >OC
课后训练
三角形中边与角之间的不等关系
知识回顾
等腰三角形的性质:
等边对等角
等边对等角
A
B
C
D
三线合一
三角形中边与边之间,角与角之间的不等关系?
在 ΔABC中,
∵ AB=AC
∴∠C=∠B
在一个三角形中,如果两条边不相等,那么它们所对的角是否相等呢?
思考
实验探究
图1
图2
② 如图2,将ΔABC折叠,使边AC落在AB上,
点C落在AB上的点C '处,折痕交BC于点D
活动:①如图1,纸片ΔABC, 其中AB >AC,
动手折叠纸片以说明∠B和∠C的大小关系
已知:如图,在△ABC中,AB > AC
求证:∠C > ∠B
证明:作∠BAC的平分线AD交BC于D.
在AB上截取AC'=AC,连结C'D.
∴△ADC ≌△ADC'(SAS)
∴∠C=∠AC ' D(全等三角形对应角相等)
∵ ∠AC ' D > ∠ B(三角形的一个外角大于任何一个和它不相邻的内角)
在 ADC与 ADC '中
∵ AC=AC ' (作图)
∠CAD= ∠C ' AD(已知)
AD=AD(公共边)
∴∠C > ∠ B
D
E
实验探究
你还能用别的折叠方法来证明吗?
E
D
A
B
C
D
E
定 理:
在一个三角形中,如果两条边不等,那么它们所对的角也不等,大边所对的角较大。
一个三角形
所对
简写成“大边对大角”
在ΔABC中, ∵ AB>AC
∴∠C > ∠B
1、在ΔABC中,已知BC > AB > AC,那么∠A,∠B,∠C的大小关系为_____________
∠A>∠C>∠B
知识运用
2、如果一个三角形中最大的边所对的角是锐角,这个三角形一定是锐角三角形吗?为什么?
知识运用
如图,在四边形ABCD中,四条
边不等,AD边最大,BC边最小
求证:∠B >∠D
牛刀小试
请谈谈你的收获
小结:
三角形中的边与角之间的不等关系
简写成:大边对大角
在⊿ABC中, ∵ AB>AC
∴∠C > ∠B
定理:在一个三角形中,如果两条边不等,那么它们所对的角也不等,大边所对的角较大。
在解决问题时,我们可以将新问题转化到我们已知的、熟悉的定理,用已有的知识解决新问题.利用轴对称的性质,可以把研究边与角之间的不等问题,转化为外角的问题,这种转化的思想是研究几何问题时常用的方法.
3、如图,在三角形△ABC中,AB>AC,P为AC延长线上一点,PD⊥BC,分别交BC、BA的延长线于D、E。判断∠E和∠P的大小关系并证明。
课后训练
1、整理做法:选出两种你喜欢的作法完成证明.
2、类比今天探究“大边对大角”的活动过程,请你探究命题“大角对大边”.
悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,去发现.去总结
下课了!
再见
结束寄语
E
D
我们的方法
D
“大边对大角”有没有逆定理?
逆命题:“大角对大边”
已知:如图,在△ABC中,∠C>∠B
求证: AC > AB
思考
已知:如图,在△ABC中,∠C > ∠B
求证:AB > AC
证明:作BC的垂直平分线MN,分别交AB、BC
于M、N,连结MC.
∴MB = MC(线段垂直平分线上的点和线段两个
端点的距离相等)
∴MA+MB > AC(等量代换)
∵MA + MC > AC(三角形的任何
两边的和大于第三边)
即AB > AC
∵MN垂直平分BC(已知)
定理及逆定理:
定理:在一个三角形中,如果两条边不等,那么它们所对的角也不等,大边所对的角较大。
一个三角形
所对
简写成“大边对大角”
逆定理:在一个三角形中,如果两个角不等,那么它们所对的边也不等,大角所对的边较大。
简写成“大角对大边”
一个三角形
所对
2、如图,AD是△ABC中∠BAC的
平分线,E在AB上,且EB = EC,
∠ACE >∠ECB,AD,EC相交
于O
求证:DC >OC
课后训练
