2022-2023学年华东师大版数学八年级上册 13.2.3 边角边 课时练习 (含答案)
文档属性
| 名称 | 2022-2023学年华东师大版数学八年级上册 13.2.3 边角边 课时练习 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 883.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-16 16:42:10 | ||
图片预览




文档简介
13.2.3 边角边(附解析)
一、单选题(共10个小题)
1.如图,AC与BD相交于点O,∠1=∠2,若用“SAS”说明△ABC≌△BAD,则还需添加的一个条件是( )
A.AD=BC B.∠C=∠D C.AO=BO D.AC=BD
2.如图①是一个直角三角形纸片,将其折叠,使点C落在斜边上的点处,折痕为,如图②,如果为AB的中点,的面积为1,则的面积为( )
A.2 B.3 C.4 D.5
3.如图,在△ABC中,,,,平分交于点,在上截取,则△BDE的周长为( )
A. B. C. D.
4.如图,在△ABC和△DEF中,AB=DE,ABDE,运用“SAS”判定△ABC≌△DEF,需补充的条件是( )
A.AC=DF B.∠A=∠D C.BE=CF D.∠ACB=∠DFE
5.如图,在△ABC和△DEF中,,补充一个条件后,能直接应用“SAS”判定的是( )
A. B. C. D.
6.如图,在2×2的方格纸中,∠1+∠2等于( )
A.60° B.90° C.120° D.150°
7.如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )
A.60° B.65° C.70° D.75°
8.如图,已知△ABC和△ECD是两个全等的等边三角形,点、、在同一条直线上,连接,,两线交于点,交于点,交于点,则下列结论正确的有( )个.
①;②;③;④是等边三角形.
A.4 B.3 C.2 D.1
9.下列选项可用SAS证明△ABC≌△A′B′C′的是( )
A.AB=A′B′,∠B=∠B′,AC=A′C′ B.AB=A′B′,BC=B′C′,∠A=∠A′
C.AC=A′C′,BC=B′C′,∠C=∠C′ D.AC=A′C′,BC=B′C′,∠B=∠B′
10.如图,在△ABC中,,,,垂足分别为D,E,AD,CE交于点H,且,下列四个结论:①;②;③;④是等腰三角形,你认为正确结论的序号是( )
A.①②③ B.①③④ C.②③④ D.①②③④
二、填空题(共10个小题)
11.如图所示,AD⊥BC,D为BC的中点,若∠B=52°,则∠C=_____.
12.如图,为了测量A、B两点之间的距离,在地面上找到一点C,连接、,使得,然后在的延长线上确定点D,使,那么只要测量出的长度就得到A、B两点之间的距离,其中的依据是__________.
13.如图所示,将两根钢条、的中点O连在一起,使、可以绕着点O自由转动,就做成了一个测量工具,则的长等于内槽宽AB,那么判定的理由是_____.
14.如图所示,若AD=AB,AC=AG,∠DAE=∠GAC=60°,则∠DOC=_______.
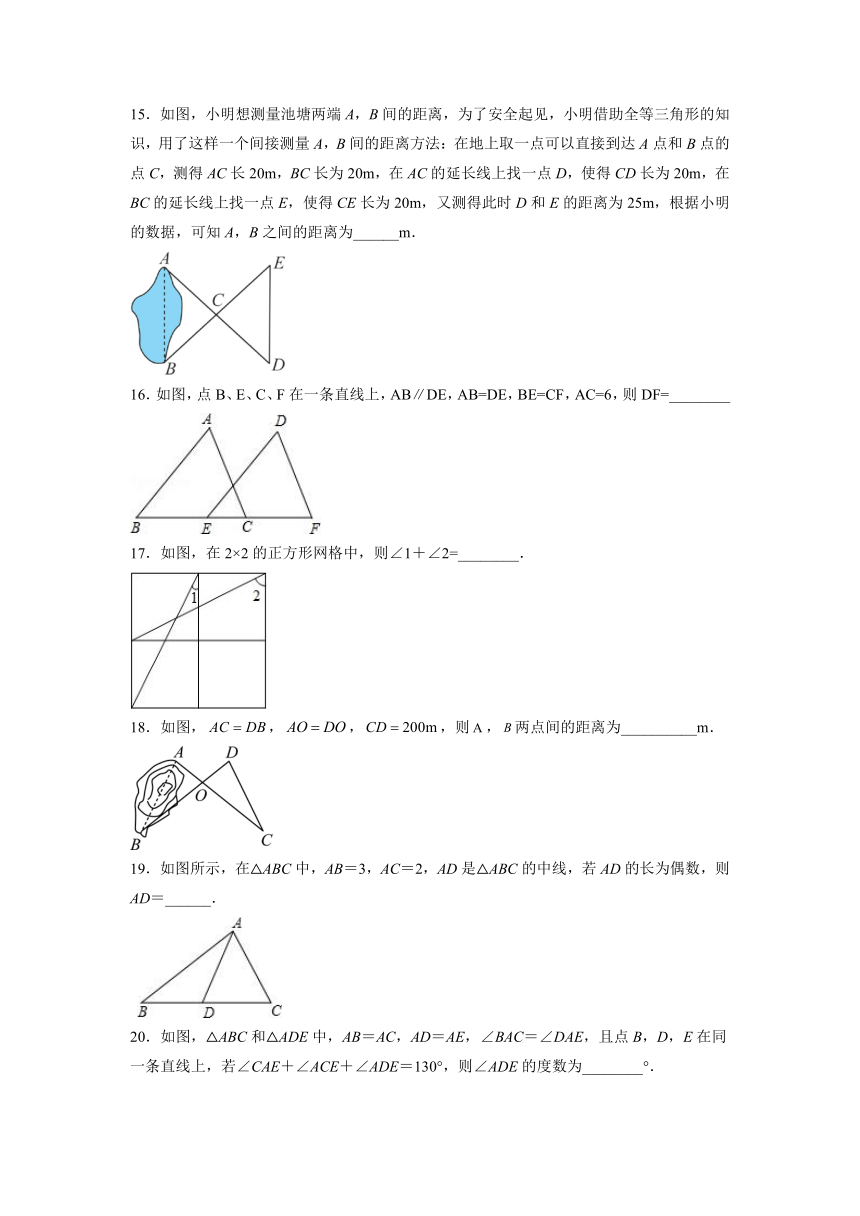
15.如图,小明想测量池塘两端A,B间的距离,为了安全起见,小明借助全等三角形的知识,用了这样一个间接测量A,B间的距离方法:在地上取一点可以直接到达A点和B点的点C,测得AC长20m,BC长为20m,在AC的延长线上找一点D,使得CD长为20m,在BC的延长线上找一点E,使得CE长为20m,又测得此时D和E的距离为25m,根据小明的数据,可知A,B之间的距离为______m.
16.如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=________
17.如图,在2×2的正方形网格中,则∠1+∠2=________.
18.如图,,,,则,两点间的距离为__________m.
19.如图所示,在△ABC中,AB=3,AC=2,AD是△ABC的中线,若AD的长为偶数,则AD=______.
20.如图,△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,D,E在同一条直线上,若∠CAE+∠ACE+∠ADE=130°,则∠ADE的度数为________°.
三、解答题(共3个小题)
21.已知点、、、在同一直线上,已知,,,试说明BE与的关系.
22.如图,在△ABC和△AEF中,点E在BC边上,AE=AB,AC=AF,∠CAF=∠BAE,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠B=62°,∠ACB=24°,求∠FGC的度数.
23.如图,已知点D、E是△ABC内两点,且.
(1)求证:△ABD≌△ACE.
(2)延长BD、CE交于点F,若,求的度数.
13.2.3 边角边解析
1.
【答案】D
【详解】解:添加AC=BD,理由如下:
在△ABC和△BAD中,
,
∴△ABC≌△BAD(SAS),
故选:D.
2.
【答案】B
【详解】解:∵△ABC为直角三角形,
∴∠C=∠==90°,
由折叠的性质得:△BCD≌△,
∴=1,
∵为AB的中点,
∴,
∵∠==90°,,
∴△ADC≌△BDC/(SAS),
∴=1,
∴=3.
故选:B.
3.
【答案】A
【详解】解:是的平分线,
在△ADE和△ADC中,
,
∴(SAS),
∴,
,,,
∴△BDE的周长:,
故选:A.
4.
【答案】C
【详解】解:补充BE=CF,理由如下:
∵AB∥DE,
∴∠ABC=∠DEF,
若要利用SAS判定,B、D选项不符合要求,
若A:AC=DF,构成的是SSA,不能证明三角形全等,A选项不符合要求,
C选项:BE=CF,
∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
故选:C.
5.
【答案】B
【详解】解:∵,,
∴(SAS)
故选B
6.
【答案】B
【详解】解:如图,在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
∴∠2=∠3,
在Rt△ABC中,∠1+∠3=90°,
∴∠1+∠2=90°.
故选:B.
7.
【答案】B
【详解】解:∵AB=AC,
∴∠B=∠C,
在△DBE和△ECF中,,
∴△DBE≌△ECF(SAS),
∴∠EFC=∠DEB,
∵∠A=50°,
∴∠C=(180° 50°)÷2=65°,
∴∠CFE+∠FEC=180° 65°=115°,
∴∠DEB+∠FEC=115°,
∴∠DEF=180° 115°=65°,
故选:B.
8.
【答案】A
【详解】解:∵△ABC和△DCE均是等边三角形,
∴BC=AC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ACE+∠ECD,∠ACE=60°,
在△BCD和△ACE中,
∴△BCE≌△ACD(SAS),故①正确
∴,
∵∠CMB=∠FMA,
∴∠BCM=∠AFM=60°,
∴∠MFN=120°,故②正确,
在△CAN和△BCM中
∴△CAN≌△BCM(ASA),故③正确,
∴MC=NC,
∵∠ACE=60°,
∴△MNC是等边三角形,故④正确
故选:A
9.
【答案】C
【详解】解:A、不满足SAS,不能证明△ABC≌△A′B′C′,不符合题意;
B、不满足SAS,不能证明△ABC≌△A′B′C′,不符合题意;
C、满足SAS,能证明△ABC≌△A′B′C′,符合题意;
D、不满足SAS,不能证明△ABC≌△A′B′C′,不符合题意,
故选:C.
10.
【答案】C
【详解】解:①假设∠ABC=45°成立,
∵AD⊥BC,
∴∠BAD=45°,
又∠BAC=45°,
矛盾,所以∠ABC=45°不成立,故本选项错误;
∵CE⊥AB,∠BAC=45度,
∴AE=EC,
在△AEH和△CEB中,
,
∴△AEH≌△CEB(SAS),
∴AH=BC,故选项②正确;
又EC-EH=CH,
∴AE-EH=CH,故选项③正确.
∵AE=CE,CE⊥AB,所以△AEC是等腰直角三角形,故选项④正确.
∴②③④正确.
故选:C.
11.
【答案】52°
【详解】解:∵
∴
∵D为BC的中点
∴
又∵
∴△ADC≌△ADB(SAS)
∴
故答案为:52°.
12.
【答案】
【详解】解:∵∠ACB=90°,
∴∠ACD=∠ACB=90°,
又∵CD=CB,AC=AC,
∴△ABC≌△ADC(SAS)
故答案为:SAS.
13.
【答案】SAS
【详解】解:∵OA=OA′,OB=OB′,∠AOB=∠A′OB′,
∴△OAB≌△OA′B′(SAS)
所以理由是SAS.
故答案为:SAS.
14.
【答案】120°
【详解】解:
在与△BAC中,
∴△DAG≌△BAC(SAS)
故答案为:
15.
【答案】25
【详解】解:由题意知,,且,
在和中,
,
,
,
,
.
故答案为:25.
16.
【答案】6.
【详解】∵AB∥DE,
∴∠B=∠DEF
∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴AC=DF=6.
17.
【答案】
【详解】解:由题意得,,,
在和△FDE中,
∴(SAS),
∴,
∵,
∴,
故答案为:.
18.
【答案】200
【详解】解:∵AC=DB,AO=DO,
∴BO=CO,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=DC,
∵CD=200m,
∴AB=200m,
即A,B两点间的距离是200m,
故答案为:200.
19.
【答案】2
【详解】解:延长至,使,连接,
在与中,
,
,
,
在中,,
即,
,
为偶数,
,
故答案为:2.
20.
【答案】65
【详解】解:∵∠BAC=∠DAE,
∴∠BAC ∠DAC=∠DAE ∠DAC,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ABD=∠ACE,
∵∠CAE+∠ACE+∠ADE=130°,
∴∠ABD+∠BAD+∠ADE=130°,
∵∠ADE=∠ABD+∠BAD,
∴2∠ADE=130°,
∴∠ADE=65°.
故答案为:65.
21.
【答案】,理由见解析
【详解】解:数量关系,位置关系.
理由:∵,
∴∠A=∠C,
又,
∴AE+EF=CF+EF,即AF=CE,
在△ADF和中,
,
∴△ADF≌
∴BE=DF,∠BEF=∠DFE,
∴.
22.
【答案】(1)证明见解析;(2)∠FGC=80°
【详解】(1)证明:∵∠CAF=∠BAE,
∴∠CAF+∠EAC=∠BAE+∠EAC,
即∠BAC=∠EAF,
在△BAC和△EAF中,
,
∴△BAC≌△EAF(SAS),
∴EF=BC.
(2)解:∵AB=AE,
∴∠B=∠AEB=62°,
∴∠BAE=56°,
∴∠CAF=∠BAE=56°,
∵△BAC≌△EAF,
∴∠F=∠C=24°,
∴∠FGC=∠FAC+∠F=56°+24°=80°.
23.
【答案】(1)证明见解析;(2)
【详解】(1)证明:∵,
∴,即,
在和△ACE中,,
∴.
(2)解:∵△ABD≌△ACE,,
∴,
,
∴,
∴,
∴.
一、单选题(共10个小题)
1.如图,AC与BD相交于点O,∠1=∠2,若用“SAS”说明△ABC≌△BAD,则还需添加的一个条件是( )
A.AD=BC B.∠C=∠D C.AO=BO D.AC=BD
2.如图①是一个直角三角形纸片,将其折叠,使点C落在斜边上的点处,折痕为,如图②,如果为AB的中点,的面积为1,则的面积为( )
A.2 B.3 C.4 D.5
3.如图,在△ABC中,,,,平分交于点,在上截取,则△BDE的周长为( )
A. B. C. D.
4.如图,在△ABC和△DEF中,AB=DE,ABDE,运用“SAS”判定△ABC≌△DEF,需补充的条件是( )
A.AC=DF B.∠A=∠D C.BE=CF D.∠ACB=∠DFE
5.如图,在△ABC和△DEF中,,补充一个条件后,能直接应用“SAS”判定的是( )
A. B. C. D.
6.如图,在2×2的方格纸中,∠1+∠2等于( )
A.60° B.90° C.120° D.150°
7.如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )
A.60° B.65° C.70° D.75°
8.如图,已知△ABC和△ECD是两个全等的等边三角形,点、、在同一条直线上,连接,,两线交于点,交于点,交于点,则下列结论正确的有( )个.
①;②;③;④是等边三角形.
A.4 B.3 C.2 D.1
9.下列选项可用SAS证明△ABC≌△A′B′C′的是( )
A.AB=A′B′,∠B=∠B′,AC=A′C′ B.AB=A′B′,BC=B′C′,∠A=∠A′
C.AC=A′C′,BC=B′C′,∠C=∠C′ D.AC=A′C′,BC=B′C′,∠B=∠B′
10.如图,在△ABC中,,,,垂足分别为D,E,AD,CE交于点H,且,下列四个结论:①;②;③;④是等腰三角形,你认为正确结论的序号是( )
A.①②③ B.①③④ C.②③④ D.①②③④
二、填空题(共10个小题)
11.如图所示,AD⊥BC,D为BC的中点,若∠B=52°,则∠C=_____.
12.如图,为了测量A、B两点之间的距离,在地面上找到一点C,连接、,使得,然后在的延长线上确定点D,使,那么只要测量出的长度就得到A、B两点之间的距离,其中的依据是__________.
13.如图所示,将两根钢条、的中点O连在一起,使、可以绕着点O自由转动,就做成了一个测量工具,则的长等于内槽宽AB,那么判定的理由是_____.
14.如图所示,若AD=AB,AC=AG,∠DAE=∠GAC=60°,则∠DOC=_______.
15.如图,小明想测量池塘两端A,B间的距离,为了安全起见,小明借助全等三角形的知识,用了这样一个间接测量A,B间的距离方法:在地上取一点可以直接到达A点和B点的点C,测得AC长20m,BC长为20m,在AC的延长线上找一点D,使得CD长为20m,在BC的延长线上找一点E,使得CE长为20m,又测得此时D和E的距离为25m,根据小明的数据,可知A,B之间的距离为______m.
16.如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=________
17.如图,在2×2的正方形网格中,则∠1+∠2=________.
18.如图,,,,则,两点间的距离为__________m.
19.如图所示,在△ABC中,AB=3,AC=2,AD是△ABC的中线,若AD的长为偶数,则AD=______.
20.如图,△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,D,E在同一条直线上,若∠CAE+∠ACE+∠ADE=130°,则∠ADE的度数为________°.
三、解答题(共3个小题)
21.已知点、、、在同一直线上,已知,,,试说明BE与的关系.
22.如图,在△ABC和△AEF中,点E在BC边上,AE=AB,AC=AF,∠CAF=∠BAE,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠B=62°,∠ACB=24°,求∠FGC的度数.
23.如图,已知点D、E是△ABC内两点,且.
(1)求证:△ABD≌△ACE.
(2)延长BD、CE交于点F,若,求的度数.
13.2.3 边角边解析
1.
【答案】D
【详解】解:添加AC=BD,理由如下:
在△ABC和△BAD中,
,
∴△ABC≌△BAD(SAS),
故选:D.
2.
【答案】B
【详解】解:∵△ABC为直角三角形,
∴∠C=∠==90°,
由折叠的性质得:△BCD≌△,
∴=1,
∵为AB的中点,
∴,
∵∠==90°,,
∴△ADC≌△BDC/(SAS),
∴=1,
∴=3.
故选:B.
3.
【答案】A
【详解】解:是的平分线,
在△ADE和△ADC中,
,
∴(SAS),
∴,
,,,
∴△BDE的周长:,
故选:A.
4.
【答案】C
【详解】解:补充BE=CF,理由如下:
∵AB∥DE,
∴∠ABC=∠DEF,
若要利用SAS判定,B、D选项不符合要求,
若A:AC=DF,构成的是SSA,不能证明三角形全等,A选项不符合要求,
C选项:BE=CF,
∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
故选:C.
5.
【答案】B
【详解】解:∵,,
∴(SAS)
故选B
6.
【答案】B
【详解】解:如图,在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
∴∠2=∠3,
在Rt△ABC中,∠1+∠3=90°,
∴∠1+∠2=90°.
故选:B.
7.
【答案】B
【详解】解:∵AB=AC,
∴∠B=∠C,
在△DBE和△ECF中,,
∴△DBE≌△ECF(SAS),
∴∠EFC=∠DEB,
∵∠A=50°,
∴∠C=(180° 50°)÷2=65°,
∴∠CFE+∠FEC=180° 65°=115°,
∴∠DEB+∠FEC=115°,
∴∠DEF=180° 115°=65°,
故选:B.
8.
【答案】A
【详解】解:∵△ABC和△DCE均是等边三角形,
∴BC=AC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ACE+∠ECD,∠ACE=60°,
在△BCD和△ACE中,
∴△BCE≌△ACD(SAS),故①正确
∴,
∵∠CMB=∠FMA,
∴∠BCM=∠AFM=60°,
∴∠MFN=120°,故②正确,
在△CAN和△BCM中
∴△CAN≌△BCM(ASA),故③正确,
∴MC=NC,
∵∠ACE=60°,
∴△MNC是等边三角形,故④正确
故选:A
9.
【答案】C
【详解】解:A、不满足SAS,不能证明△ABC≌△A′B′C′,不符合题意;
B、不满足SAS,不能证明△ABC≌△A′B′C′,不符合题意;
C、满足SAS,能证明△ABC≌△A′B′C′,符合题意;
D、不满足SAS,不能证明△ABC≌△A′B′C′,不符合题意,
故选:C.
10.
【答案】C
【详解】解:①假设∠ABC=45°成立,
∵AD⊥BC,
∴∠BAD=45°,
又∠BAC=45°,
矛盾,所以∠ABC=45°不成立,故本选项错误;
∵CE⊥AB,∠BAC=45度,
∴AE=EC,
在△AEH和△CEB中,
,
∴△AEH≌△CEB(SAS),
∴AH=BC,故选项②正确;
又EC-EH=CH,
∴AE-EH=CH,故选项③正确.
∵AE=CE,CE⊥AB,所以△AEC是等腰直角三角形,故选项④正确.
∴②③④正确.
故选:C.
11.
【答案】52°
【详解】解:∵
∴
∵D为BC的中点
∴
又∵
∴△ADC≌△ADB(SAS)
∴
故答案为:52°.
12.
【答案】
【详解】解:∵∠ACB=90°,
∴∠ACD=∠ACB=90°,
又∵CD=CB,AC=AC,
∴△ABC≌△ADC(SAS)
故答案为:SAS.
13.
【答案】SAS
【详解】解:∵OA=OA′,OB=OB′,∠AOB=∠A′OB′,
∴△OAB≌△OA′B′(SAS)
所以理由是SAS.
故答案为:SAS.
14.
【答案】120°
【详解】解:
在与△BAC中,
∴△DAG≌△BAC(SAS)
故答案为:
15.
【答案】25
【详解】解:由题意知,,且,
在和中,
,
,
,
,
.
故答案为:25.
16.
【答案】6.
【详解】∵AB∥DE,
∴∠B=∠DEF
∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴AC=DF=6.
17.
【答案】
【详解】解:由题意得,,,
在和△FDE中,
∴(SAS),
∴,
∵,
∴,
故答案为:.
18.
【答案】200
【详解】解:∵AC=DB,AO=DO,
∴BO=CO,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=DC,
∵CD=200m,
∴AB=200m,
即A,B两点间的距离是200m,
故答案为:200.
19.
【答案】2
【详解】解:延长至,使,连接,
在与中,
,
,
,
在中,,
即,
,
为偶数,
,
故答案为:2.
20.
【答案】65
【详解】解:∵∠BAC=∠DAE,
∴∠BAC ∠DAC=∠DAE ∠DAC,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ABD=∠ACE,
∵∠CAE+∠ACE+∠ADE=130°,
∴∠ABD+∠BAD+∠ADE=130°,
∵∠ADE=∠ABD+∠BAD,
∴2∠ADE=130°,
∴∠ADE=65°.
故答案为:65.
21.
【答案】,理由见解析
【详解】解:数量关系,位置关系.
理由:∵,
∴∠A=∠C,
又,
∴AE+EF=CF+EF,即AF=CE,
在△ADF和中,
,
∴△ADF≌
∴BE=DF,∠BEF=∠DFE,
∴.
22.
【答案】(1)证明见解析;(2)∠FGC=80°
【详解】(1)证明:∵∠CAF=∠BAE,
∴∠CAF+∠EAC=∠BAE+∠EAC,
即∠BAC=∠EAF,
在△BAC和△EAF中,
,
∴△BAC≌△EAF(SAS),
∴EF=BC.
(2)解:∵AB=AE,
∴∠B=∠AEB=62°,
∴∠BAE=56°,
∴∠CAF=∠BAE=56°,
∵△BAC≌△EAF,
∴∠F=∠C=24°,
∴∠FGC=∠FAC+∠F=56°+24°=80°.
23.
【答案】(1)证明见解析;(2)
【详解】(1)证明:∵,
∴,即,
在和△ACE中,,
∴.
(2)解:∵△ABD≌△ACE,,
∴,
,
∴,
∴,
∴.
