2022-2023学年华东师大版数学八年级上册 13.2.4 角边角 课时练习 (含答案)
文档属性
| 名称 | 2022-2023学年华东师大版数学八年级上册 13.2.4 角边角 课时练习 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 876.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-16 16:43:37 | ||
图片预览



文档简介
13.2.4 角边角(附解析)
一、单选题(共10个小题)
1.如图,D是AB上一点,DF交AC于点E,DE=EF,FC∥AB,若AB=8,CF=6,则BD的长是( )
A.1 B.2 C.3 D.4
2.如图,BO、CO分别平分∠ABC、∠ACB,OD⊥BC于点D,OD=2,△ABC的周长为28,则△ABC的面积为( )
A.28 B.14 C.21 D.7
3.如图,甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.甲和丙 C.乙和丙 D.只有丙
4.在ΔABC中给定下面几组条件:
①∠ACB=30°,BC=4cm,AC=5cm ②∠ABC=30°,BC=4cm,AC=3cm
③∠ABC=90°,BC=4cm,AC=5cm ④∠ABC=120°,BC=4cm,AC=5cm
若根据每组条件画图,则ΔABC不能够唯一确定的是( )
A.① B.② C.③ D.④
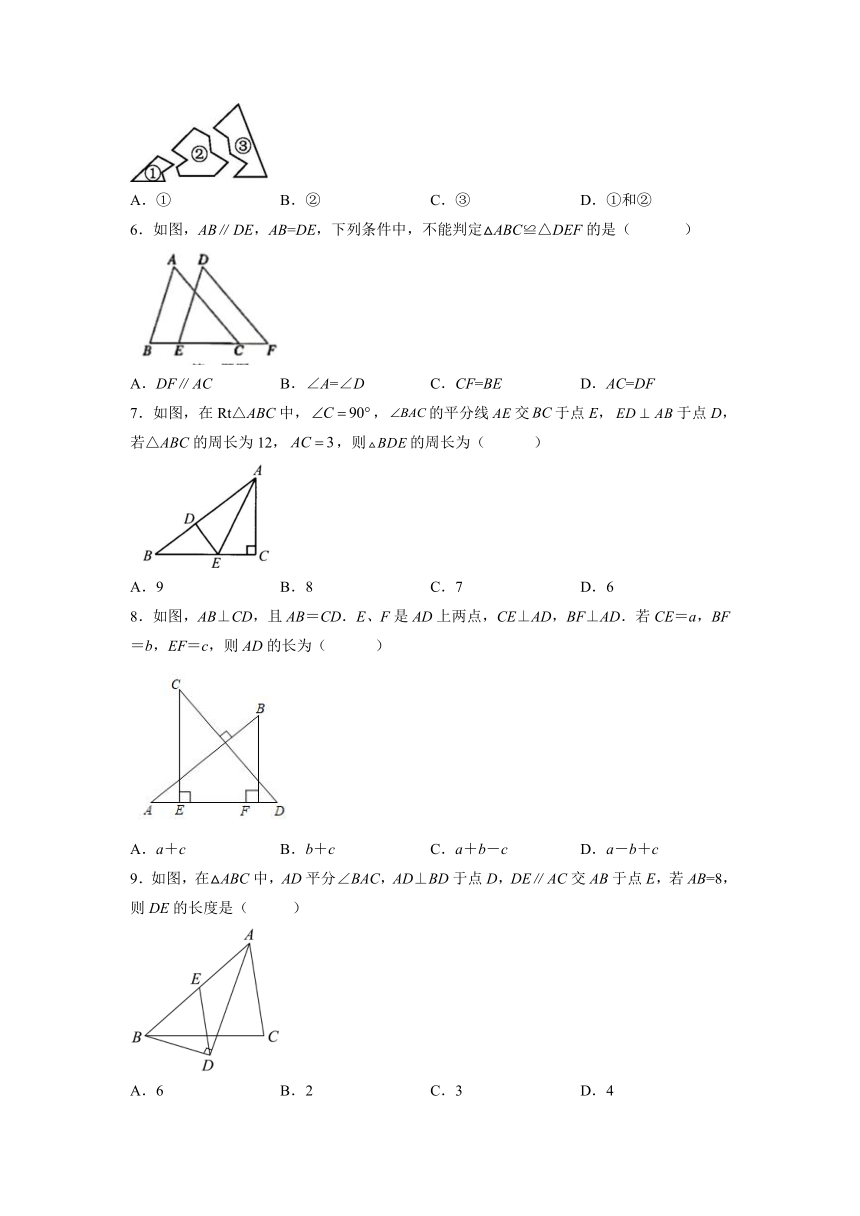
5.如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪一块去( )
A.① B.② C.③ D.①和②
6.如图,ABDE,AB=DE,下列条件中,不能判定△ABC≌△DEF的是( )
A.DFAC B.∠A=∠D C.CF=BE D.AC=DF
7.如图,在Rt△ABC中,,的平分线交于点E,于点D,若△ABC的周长为12,,则的周长为( )
A.9 B.8 C.7 D.6
8.如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
A.a+c B.b+c C.a+b-c D.a-b+c
9.如图,在△ABC中,AD平分∠BAC,AD⊥BD于点D,DEAC交AB于点E,若AB=8,则DE的长度是( )
A.6 B.2 C.3 D.4
10.如图,在△ABC中,AB=BC,,点D是BC的中点,BF⊥AD,垂足为E,BF交AC于点F,连接DF.下列结论正确的是( )
A.∠1=∠3 B.∠2=∠3 C.∠3=∠4 D.∠4=∠5
二、填空题(共10个小题)
11.如图,亮亮书上的三角形被墨迹污染了一部分,借助剩余的图形,他很快就画出一个三角形与书上的三角形全等,这两个三角形全等的依据是______.
12.如图,△ABC中,AB=13cm,BC=11cm,AC=6cm,点E是BC边的中点,点D在AB边上,现将△DBE沿着BA方向向左平移至△ADF的位置,则四边形DECF的周长为_____cm.
13.如图,小明把一块三角形的玻璃片打碎成三块,现要到玻璃店去配一块完全相同的玻璃片,那么最省事的办法是带_________去.
14.如图,在中,,于点E,于点D,请你添加一个条件__________,使(填一个即可).
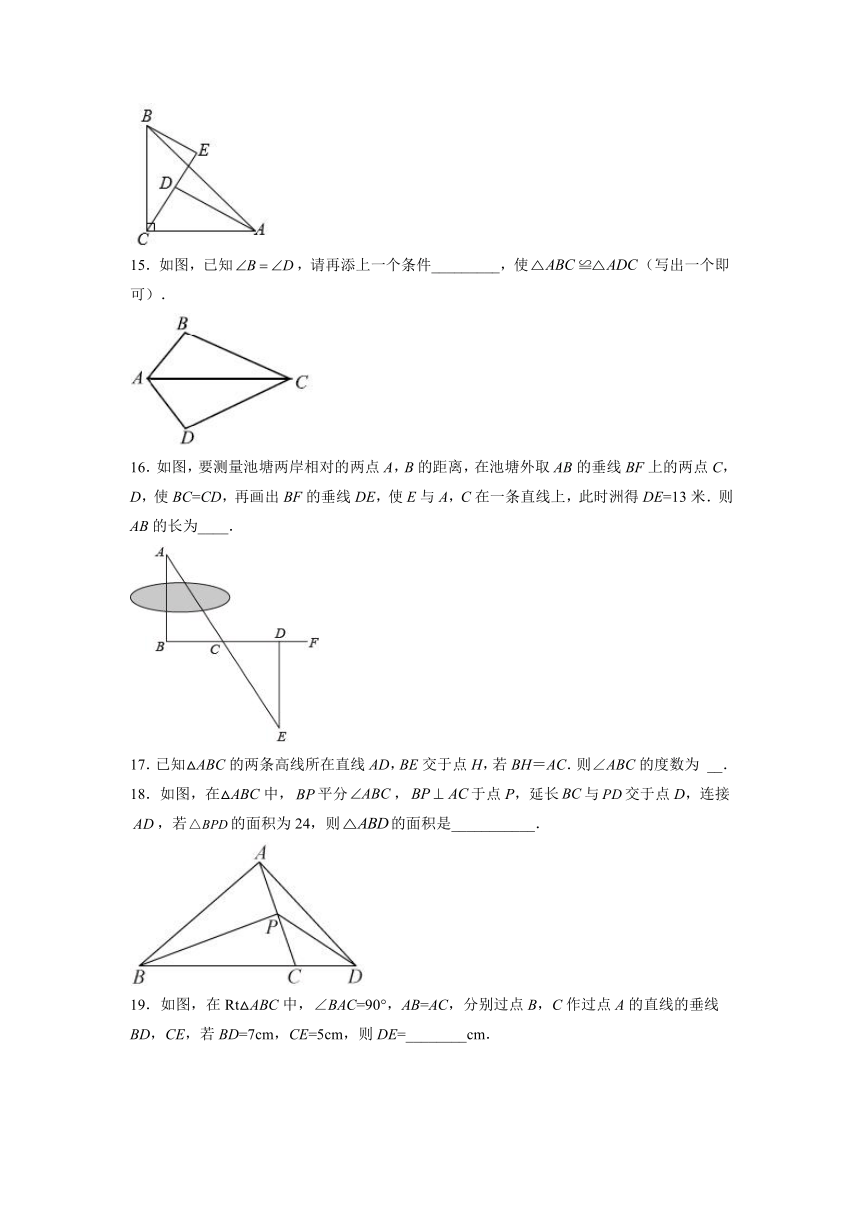
15.如图,已知,请再添上一个条件_________,使(写出一个即可).
16.如图,要测量池塘两岸相对的两点A,B的距离,在池塘外取AB的垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,此时洲得DE=13米.则AB的长为____.
17.已知△ABC的两条高线所在直线AD,BE交于点H,若BH=AC.则∠ABC的度数为 __.
18.如图,在△ABC中,平分,于点P,延长与交于点D,连接,若的面积为24,则的面积是___________.
19.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=7cm,CE=5cm,则DE=________cm.
20.如图,在等腰直角三角形中,,,D是边上的一点,过点B,C作,分别交于E,F,若,,则_______.
三、解答题(共3个小题)
21.如图,点A、B、C、D在一条直线上,AB=CD,∠A=∠FBD,CE∥DF,求证:CE=DF.
22.如图,在 ABC,∠BAC=90度,AB=AC,AE是过点A的一条直线,且B,C在AE的异侧,BD⊥AE,CE⊥AE于点E.
(1)BD=DE+CE成立吗?成立请求证,不成立请说明理由
(2)若直线AE绕点A旋转到如图2位置时,其他条件不变,BD与DE,CE关系如何?请说明理由
23.已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD垂直于直线m,CE垂直于直线m,垂足分别为点D、E.
(1)图中的一对全等三角形为 ,DE、BD和CE之间的数量关系为
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有,其中为任意钝角,请问(1)中DE、BD和CE三者之间的数量关系是否成立?若成立,请你给出证明:若不成立,请说明理由.
(3)如图③,将(1)中直线m绕点A旋转,交线段BC与点F,请直接写出DE、BD和CE之间的数量关系.
13.2.4 角边角解析
1.
【答案】B
【详解】解:∵FCAB,
∴∠A=∠FCE,∠ADE=∠F,
在△ADE与△CFE中,
,
∴△ADE≌△CFE(AAS),
∴AD=CF,
∵AB=8,CF=6,
∴BD=AB-AD=AB-CF=8-6=2,
故选:B.
2.
【答案】A
【详解】解:连接OA,过点O作于点E,作于点F,如图
∵BO平分,,,
在△BOD和中,
,
∴,
∴OE=OD=2
同理:OF=OD=2
∴OE=OF=OD=2
∵
=
=28
∴
故选:A.
3.
【答案】C
【详解】解:在△ABC和乙的三角形中,两边及其夹角对应相等,满足三角形全等的判定方法:SAS,
所以乙和△ABC全等;
在△ABC和丙的三角形中,两个及一角对边对应相等,满足三角形全等的判定方法:AAS,
所以丙和△ABC全等;
在△ABC和甲的三角形中,只有一边一角对应相等南,不能判定甲与△ABC全等;
故选:C.
4.
【答案】B
【详解】解:①BC=4cm,AC=5cm,∠ACB=30°,满足“SAS”,所以根据这组条件画图,△ABC唯一;
②BC=4cm,AC=3cm,∠ABC=30°,根据这组条件画图,△ABC可能为锐角三角形,也可为钝角三角形;
③BC=4cm,AC=5cm,∠ABC=90°;满足“HL”,所以根据这组条件画图,△ABC唯一;
④BC=4cm,AC=5cm,∠ABC=120°,根据这组条件画图,△ABC唯一.
所以,ΔABC不能够唯一确定的是②.
故选:B
5.
【答案】C
【详解】解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去.故选:C.
6.
【答案】D
【详解】A. 由DF∥AC可得∠ACB=∠DFE,由AB∥DE,可得∠ABC=∠DEF,又因 AB=DE,利用AAS可得△ABC≌△DEF,故本选项不符合题意;
B. 由AB∥DE,可得∠ABC=∠DEF,又因∠A=∠D,AB=DE,利用ASA可得△ABC≌△DEF,故本选项不符合题意;
C. 由CF=BE 可证得BC=EF ,由AB∥DE,可得∠ABC=∠DEF,又因AB=DE,利用SAS可得△ABC≌△DEF,故本选项不符合题意;
D. AC=DF ,AB∥DE,AB=DE,是SSA,不能判断三角形全等,故本选项符合题意,
故选D.
7.
【答案】D
【详解】解:∵平分
∴,
又∵
∴
又∵
∴(AAS)
∴、,
△BDE的周长为
,
故选:D
8.
【答案】C
【详解】解:∵,,,
∴,,,
∴.
∵,,,
∴≌,
∴,.
∵,
∴.
故选:C.
9.
【答案】D
【详解】解:分别延长AC、BD交于点F,
∵AD平分∠BAC,AD⊥BD,
∴∠BAD=∠FAD,∠ADB=∠ADF=90°,
在△BAD和△FAD中,,
∴△BAD≌△FAD(ASA),
∴∠ABD=∠F,
∵DEAC,
∴∠EDB=∠F,∠EDA=∠FAD,
∴∠ABD=∠EDB,∠EDA=∠EAD,
∴BE=ED,EA=ED,
∴BE=EA=ED,
∴DE=AB=×8=4,
故选:D.
10.
【答案】A
【详解】如图,过点C作BC的垂线,交BF的延长线于点G,则,即
在和中,
点D是BC的中点
在和中,
故选:A.
11.
【答案】ASA
【详解】解:根据图形可知上方和右下的角还能确定,右边的边也能确定,属于两角及其夹边能确定,即ASA模型.
故答案是:ASA.
12.
【答案】17
【详解】解:连接EF.
由平移的性质可知,AF=DE.EF=AD,AF∥DE,EF∥AD,DF∥BC,
∴∠CEF=∠DFE,∠CFE=∠DEF,
在△CEF和△DFE中,
,
∴△CEF≌△DFE(ASA),
∴DE=CF,
∴AF=CF=DE=3cm
∵E是BC的中点,
∴EC=EB=DF=5.5cm,
∴四边形DECF的周长=2(3+5.5)=17cm.
故答案为:17.
13.
【答案】③
【详解】解:第①块和第②块都没有保留完整的边,而全等三角形的判定定理中,至少存在一条边,第③块保留了一边边和两个角,则利用ASA判定定理可得到一个全等三角形,进而可带③去,
故答案为:③.
14.
【答案】(答案不唯一)
【详解】解:添加的条件是,
,,
,
,
,
,
在和中,
,
.
故答案为:(答案不唯一).
15.
【答案】
【详解】添加一个条件:,
证明:在三角形△ABC和△ADC中 ,
∴
故答案为:
16.
【答案】13米
【详解】解:在和中,
∴(ASA),
∴,
故答案为:13米.
17.
【答案】45°或135°
【详解】解:分为两种情况:
①如图1,
∵AD、BE是△ABC的高,
∴∠ADC=∠BDH=90°,∠BEC=90°,
∴∠C+∠CAD=90°,∠C+∠HBD=90°,
∴∠CAD=∠HBD,
在△HBD和△CAD中
,
∴△HBD≌△CAD(AAS),
∴BD=AD,
∵∠ADB=90°,
∴∠ABC=∠BAD=45°,
②如图2,
∵AD⊥BC,BE⊥AC,
∴∠ADC=∠HDB=∠AEH=90°,
∴∠H+∠HAE=∠C+∠HAE=90°,
∴∠H=∠C,
∵在△HBD和△CAD中,
,
∴△HBD≌△CAD(AAS),
∴AD=BD,
∴∠DAB=∠DBA,
∵∠ADB=90°,
∴∠ABD=45°,
∴∠ABC=180°﹣45°=135°;
故答案为:45°或135°.
18.
【答案】48
【详解】解:∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵BP⊥AC于点P,
∴∠APB=∠CPB,
在△ABP和△CBP中,
∴△ABP≌△CBP(ASA),
∴AP=CP,
∴△ABP的面积等于△CBP的面积,△ADP的面积等于△CPD的面积,
∴S△ABD=2S△BPD,
∵△BPD的面积为24,
∴△ABD的面积为48.
故答案为:48.
19.
【答案】12
【详解】∵∠BAC=90°,∠ADB=∠AEC=90°,
∴∠BAD+∠EAC=90°,∠BAD+∠ABD=90°,
∴∠EAC=∠ABD,
∵AB=AC,
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE,
∴DE=AD+AE=CE+BD=12cm.
故答案为:12.
20.
【答案】1.2
【详解】解:∵,,
∴,
∵,
∴,即,
∵,
∴(AAS),
∵,,
∴,
∴;
故答案为1.2.
21.
【答案】见解析
【详解】证明:∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD,
∵CE∥DF,
∴∠D=∠ECA,
在△AEC与△BFD中,
,
∴△AEC≌△BFD(ASA),
∴CE=DF.
22.
【答案】(1)成立,证明见解析;(2)BD=DE CE,理由见解析.
【详解】(1)解:成立,
证明:∵∠BAC=90°,BD⊥AE,
∴∠CAD+∠BAD=90°,∠BAD+∠ABD=90°,
∴∠CAD=∠ABD,
在△ABD和△CAE中,,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
又∵AE=AD+DE,
∴AE=DE+CE,
∴BD=DE+CE;
(2)BD=DE CE,
理由:∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥DE,
∴∠BAD+∠ABD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵DE=AD+AE,
∴DE=CE+BD,
∴BD=DE CE.
23.
【答案】(1)△ADB≌△CEA;DE=BD+CE;(2)结论DE=BD+CE成立,证明见解析;(3)DE=BD-CE.
【详解】(1)解:图中的一对全等三角形为:△ADB≌△CEA;DE、BD和CE之间的数量关系为:DE=BD+CE;
证明:如图①,∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE,
故答案为:△ADB≌△CEA;DE=BD+CE;
(2)结论DE=BD+CE成立,
证明:如图②,∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180° α,
∴∠DBA=∠CAE,
在△ADB和△CEA中,,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(3)如图③,∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE-AD=BD-CE.
一、单选题(共10个小题)
1.如图,D是AB上一点,DF交AC于点E,DE=EF,FC∥AB,若AB=8,CF=6,则BD的长是( )
A.1 B.2 C.3 D.4
2.如图,BO、CO分别平分∠ABC、∠ACB,OD⊥BC于点D,OD=2,△ABC的周长为28,则△ABC的面积为( )
A.28 B.14 C.21 D.7
3.如图,甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.甲和丙 C.乙和丙 D.只有丙
4.在ΔABC中给定下面几组条件:
①∠ACB=30°,BC=4cm,AC=5cm ②∠ABC=30°,BC=4cm,AC=3cm
③∠ABC=90°,BC=4cm,AC=5cm ④∠ABC=120°,BC=4cm,AC=5cm
若根据每组条件画图,则ΔABC不能够唯一确定的是( )
A.① B.② C.③ D.④
5.如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪一块去( )
A.① B.② C.③ D.①和②
6.如图,ABDE,AB=DE,下列条件中,不能判定△ABC≌△DEF的是( )
A.DFAC B.∠A=∠D C.CF=BE D.AC=DF
7.如图,在Rt△ABC中,,的平分线交于点E,于点D,若△ABC的周长为12,,则的周长为( )
A.9 B.8 C.7 D.6
8.如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
A.a+c B.b+c C.a+b-c D.a-b+c
9.如图,在△ABC中,AD平分∠BAC,AD⊥BD于点D,DEAC交AB于点E,若AB=8,则DE的长度是( )
A.6 B.2 C.3 D.4
10.如图,在△ABC中,AB=BC,,点D是BC的中点,BF⊥AD,垂足为E,BF交AC于点F,连接DF.下列结论正确的是( )
A.∠1=∠3 B.∠2=∠3 C.∠3=∠4 D.∠4=∠5
二、填空题(共10个小题)
11.如图,亮亮书上的三角形被墨迹污染了一部分,借助剩余的图形,他很快就画出一个三角形与书上的三角形全等,这两个三角形全等的依据是______.
12.如图,△ABC中,AB=13cm,BC=11cm,AC=6cm,点E是BC边的中点,点D在AB边上,现将△DBE沿着BA方向向左平移至△ADF的位置,则四边形DECF的周长为_____cm.
13.如图,小明把一块三角形的玻璃片打碎成三块,现要到玻璃店去配一块完全相同的玻璃片,那么最省事的办法是带_________去.
14.如图,在中,,于点E,于点D,请你添加一个条件__________,使(填一个即可).
15.如图,已知,请再添上一个条件_________,使(写出一个即可).
16.如图,要测量池塘两岸相对的两点A,B的距离,在池塘外取AB的垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,此时洲得DE=13米.则AB的长为____.
17.已知△ABC的两条高线所在直线AD,BE交于点H,若BH=AC.则∠ABC的度数为 __.
18.如图,在△ABC中,平分,于点P,延长与交于点D,连接,若的面积为24,则的面积是___________.
19.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=7cm,CE=5cm,则DE=________cm.
20.如图,在等腰直角三角形中,,,D是边上的一点,过点B,C作,分别交于E,F,若,,则_______.
三、解答题(共3个小题)
21.如图,点A、B、C、D在一条直线上,AB=CD,∠A=∠FBD,CE∥DF,求证:CE=DF.
22.如图,在 ABC,∠BAC=90度,AB=AC,AE是过点A的一条直线,且B,C在AE的异侧,BD⊥AE,CE⊥AE于点E.
(1)BD=DE+CE成立吗?成立请求证,不成立请说明理由
(2)若直线AE绕点A旋转到如图2位置时,其他条件不变,BD与DE,CE关系如何?请说明理由
23.已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD垂直于直线m,CE垂直于直线m,垂足分别为点D、E.
(1)图中的一对全等三角形为 ,DE、BD和CE之间的数量关系为
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有,其中为任意钝角,请问(1)中DE、BD和CE三者之间的数量关系是否成立?若成立,请你给出证明:若不成立,请说明理由.
(3)如图③,将(1)中直线m绕点A旋转,交线段BC与点F,请直接写出DE、BD和CE之间的数量关系.
13.2.4 角边角解析
1.
【答案】B
【详解】解:∵FCAB,
∴∠A=∠FCE,∠ADE=∠F,
在△ADE与△CFE中,
,
∴△ADE≌△CFE(AAS),
∴AD=CF,
∵AB=8,CF=6,
∴BD=AB-AD=AB-CF=8-6=2,
故选:B.
2.
【答案】A
【详解】解:连接OA,过点O作于点E,作于点F,如图
∵BO平分,,,
在△BOD和中,
,
∴,
∴OE=OD=2
同理:OF=OD=2
∴OE=OF=OD=2
∵
=
=28
∴
故选:A.
3.
【答案】C
【详解】解:在△ABC和乙的三角形中,两边及其夹角对应相等,满足三角形全等的判定方法:SAS,
所以乙和△ABC全等;
在△ABC和丙的三角形中,两个及一角对边对应相等,满足三角形全等的判定方法:AAS,
所以丙和△ABC全等;
在△ABC和甲的三角形中,只有一边一角对应相等南,不能判定甲与△ABC全等;
故选:C.
4.
【答案】B
【详解】解:①BC=4cm,AC=5cm,∠ACB=30°,满足“SAS”,所以根据这组条件画图,△ABC唯一;
②BC=4cm,AC=3cm,∠ABC=30°,根据这组条件画图,△ABC可能为锐角三角形,也可为钝角三角形;
③BC=4cm,AC=5cm,∠ABC=90°;满足“HL”,所以根据这组条件画图,△ABC唯一;
④BC=4cm,AC=5cm,∠ABC=120°,根据这组条件画图,△ABC唯一.
所以,ΔABC不能够唯一确定的是②.
故选:B
5.
【答案】C
【详解】解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去.故选:C.
6.
【答案】D
【详解】A. 由DF∥AC可得∠ACB=∠DFE,由AB∥DE,可得∠ABC=∠DEF,又因 AB=DE,利用AAS可得△ABC≌△DEF,故本选项不符合题意;
B. 由AB∥DE,可得∠ABC=∠DEF,又因∠A=∠D,AB=DE,利用ASA可得△ABC≌△DEF,故本选项不符合题意;
C. 由CF=BE 可证得BC=EF ,由AB∥DE,可得∠ABC=∠DEF,又因AB=DE,利用SAS可得△ABC≌△DEF,故本选项不符合题意;
D. AC=DF ,AB∥DE,AB=DE,是SSA,不能判断三角形全等,故本选项符合题意,
故选D.
7.
【答案】D
【详解】解:∵平分
∴,
又∵
∴
又∵
∴(AAS)
∴、,
△BDE的周长为
,
故选:D
8.
【答案】C
【详解】解:∵,,,
∴,,,
∴.
∵,,,
∴≌,
∴,.
∵,
∴.
故选:C.
9.
【答案】D
【详解】解:分别延长AC、BD交于点F,
∵AD平分∠BAC,AD⊥BD,
∴∠BAD=∠FAD,∠ADB=∠ADF=90°,
在△BAD和△FAD中,,
∴△BAD≌△FAD(ASA),
∴∠ABD=∠F,
∵DEAC,
∴∠EDB=∠F,∠EDA=∠FAD,
∴∠ABD=∠EDB,∠EDA=∠EAD,
∴BE=ED,EA=ED,
∴BE=EA=ED,
∴DE=AB=×8=4,
故选:D.
10.
【答案】A
【详解】如图,过点C作BC的垂线,交BF的延长线于点G,则,即
在和中,
点D是BC的中点
在和中,
故选:A.
11.
【答案】ASA
【详解】解:根据图形可知上方和右下的角还能确定,右边的边也能确定,属于两角及其夹边能确定,即ASA模型.
故答案是:ASA.
12.
【答案】17
【详解】解:连接EF.
由平移的性质可知,AF=DE.EF=AD,AF∥DE,EF∥AD,DF∥BC,
∴∠CEF=∠DFE,∠CFE=∠DEF,
在△CEF和△DFE中,
,
∴△CEF≌△DFE(ASA),
∴DE=CF,
∴AF=CF=DE=3cm
∵E是BC的中点,
∴EC=EB=DF=5.5cm,
∴四边形DECF的周长=2(3+5.5)=17cm.
故答案为:17.
13.
【答案】③
【详解】解:第①块和第②块都没有保留完整的边,而全等三角形的判定定理中,至少存在一条边,第③块保留了一边边和两个角,则利用ASA判定定理可得到一个全等三角形,进而可带③去,
故答案为:③.
14.
【答案】(答案不唯一)
【详解】解:添加的条件是,
,,
,
,
,
,
在和中,
,
.
故答案为:(答案不唯一).
15.
【答案】
【详解】添加一个条件:,
证明:在三角形△ABC和△ADC中 ,
∴
故答案为:
16.
【答案】13米
【详解】解:在和中,
∴(ASA),
∴,
故答案为:13米.
17.
【答案】45°或135°
【详解】解:分为两种情况:
①如图1,
∵AD、BE是△ABC的高,
∴∠ADC=∠BDH=90°,∠BEC=90°,
∴∠C+∠CAD=90°,∠C+∠HBD=90°,
∴∠CAD=∠HBD,
在△HBD和△CAD中
,
∴△HBD≌△CAD(AAS),
∴BD=AD,
∵∠ADB=90°,
∴∠ABC=∠BAD=45°,
②如图2,
∵AD⊥BC,BE⊥AC,
∴∠ADC=∠HDB=∠AEH=90°,
∴∠H+∠HAE=∠C+∠HAE=90°,
∴∠H=∠C,
∵在△HBD和△CAD中,
,
∴△HBD≌△CAD(AAS),
∴AD=BD,
∴∠DAB=∠DBA,
∵∠ADB=90°,
∴∠ABD=45°,
∴∠ABC=180°﹣45°=135°;
故答案为:45°或135°.
18.
【答案】48
【详解】解:∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵BP⊥AC于点P,
∴∠APB=∠CPB,
在△ABP和△CBP中,
∴△ABP≌△CBP(ASA),
∴AP=CP,
∴△ABP的面积等于△CBP的面积,△ADP的面积等于△CPD的面积,
∴S△ABD=2S△BPD,
∵△BPD的面积为24,
∴△ABD的面积为48.
故答案为:48.
19.
【答案】12
【详解】∵∠BAC=90°,∠ADB=∠AEC=90°,
∴∠BAD+∠EAC=90°,∠BAD+∠ABD=90°,
∴∠EAC=∠ABD,
∵AB=AC,
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE,
∴DE=AD+AE=CE+BD=12cm.
故答案为:12.
20.
【答案】1.2
【详解】解:∵,,
∴,
∵,
∴,即,
∵,
∴(AAS),
∵,,
∴,
∴;
故答案为1.2.
21.
【答案】见解析
【详解】证明:∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD,
∵CE∥DF,
∴∠D=∠ECA,
在△AEC与△BFD中,
,
∴△AEC≌△BFD(ASA),
∴CE=DF.
22.
【答案】(1)成立,证明见解析;(2)BD=DE CE,理由见解析.
【详解】(1)解:成立,
证明:∵∠BAC=90°,BD⊥AE,
∴∠CAD+∠BAD=90°,∠BAD+∠ABD=90°,
∴∠CAD=∠ABD,
在△ABD和△CAE中,,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
又∵AE=AD+DE,
∴AE=DE+CE,
∴BD=DE+CE;
(2)BD=DE CE,
理由:∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥DE,
∴∠BAD+∠ABD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵DE=AD+AE,
∴DE=CE+BD,
∴BD=DE CE.
23.
【答案】(1)△ADB≌△CEA;DE=BD+CE;(2)结论DE=BD+CE成立,证明见解析;(3)DE=BD-CE.
【详解】(1)解:图中的一对全等三角形为:△ADB≌△CEA;DE、BD和CE之间的数量关系为:DE=BD+CE;
证明:如图①,∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE,
故答案为:△ADB≌△CEA;DE=BD+CE;
(2)结论DE=BD+CE成立,
证明:如图②,∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180° α,
∴∠DBA=∠CAE,
在△ADB和△CEA中,,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(3)如图③,∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE-AD=BD-CE.
