2022-2023学年八年级华东师大版数学上册 13.2.5 边边边 课时练习 (含答案)
文档属性
| 名称 | 2022-2023学年八年级华东师大版数学上册 13.2.5 边边边 课时练习 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 703.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-16 00:00:00 | ||
图片预览

文档简介
13.2.5 边边边(附解析)
一、单选题(共10个小题)
1.如图,AB=AC,DB=DC则直接由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△EBD≌△ECD D.以上答案都不对
2.如图,已知AB=AC,AE=AD,要利用“SSS”推理得出△ABD≌△ACE,还需要添加的一个条件是( )
A.∠B=∠C B.BD=CE C.∠BAD=∠CAE D.以上都不对
3.如下图,在和中,,,则能说明≌的依据是( )
A.SSS B.ASA C.AAS D.SAS
4.如图,这是一个平分角的仪器,,将点A放在一个角的顶点,使AB、AD分别与这个角的两边重合,可证,从而得到AC就是这个角的平分线.其中证明的数学依据是( )
A.SSS B.ASA C.SAS D.AAS
5.如图,已知,则的理由是( )
A. B. C. D.
6.如图,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或② B.②或③ C.①或③ D.①或④
7.如图,AD=BC,AE=CF.E、F是BD上两点,BE=DF,∠AEB=100°,∠ADB=30°,则∠BCF的度数为( )
A.30° B.60° C.70° D.80°
8.如图,在方格纸中,以为一边作,使之与全等,从,,,四个点中找出符合条件的点,则点有( )
A.个 B.个 C.个 D.个
9.两组邻边分别相等的四边形叫做“筝形”,如图,四边形是一个筝形,其中,,在探究筝形的性质时,得到如下结论:①;②;③四边形的面积,其中正确的结论有( )
A.个 B.个 C.个 D.个
10.如图,已知,,且平分,那么图中全等三角形共有
A.2对 B.3对 C.4对 D.5对
二、填空题(共10个小题)
11.如图,AB=AC,BE=CD,要使,依据SSS,则还需添加条件_______________.(填一个即可)
12.如图,AC、BD相交于点O,OA=OB,OC=OD,则图中全等三角形共有______对.
13.如图,点,在线段上,且,,,连接,,,,则图中共有_______对全等三角形.
14.如图,AB=CB,AD=CD 根据__________可得到△ABD_______△CBD.
15.已知,如图,AD=AC,BD=BC,O为AB上一点,那么图中共有_______对全等三角形.
16.如图,在△ACD与△BCE中,AD与BE相交于点P,若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠APB的度数为__________.
17.如图,点B、C、E三点在同一直线上,且AB=AD,AC=AE,BC=DE,若,则∠3=________°.
18.如图,,,O为BD中点,过O点作直线与DA、BC延长线交于E,F,若,,则_________,_________.
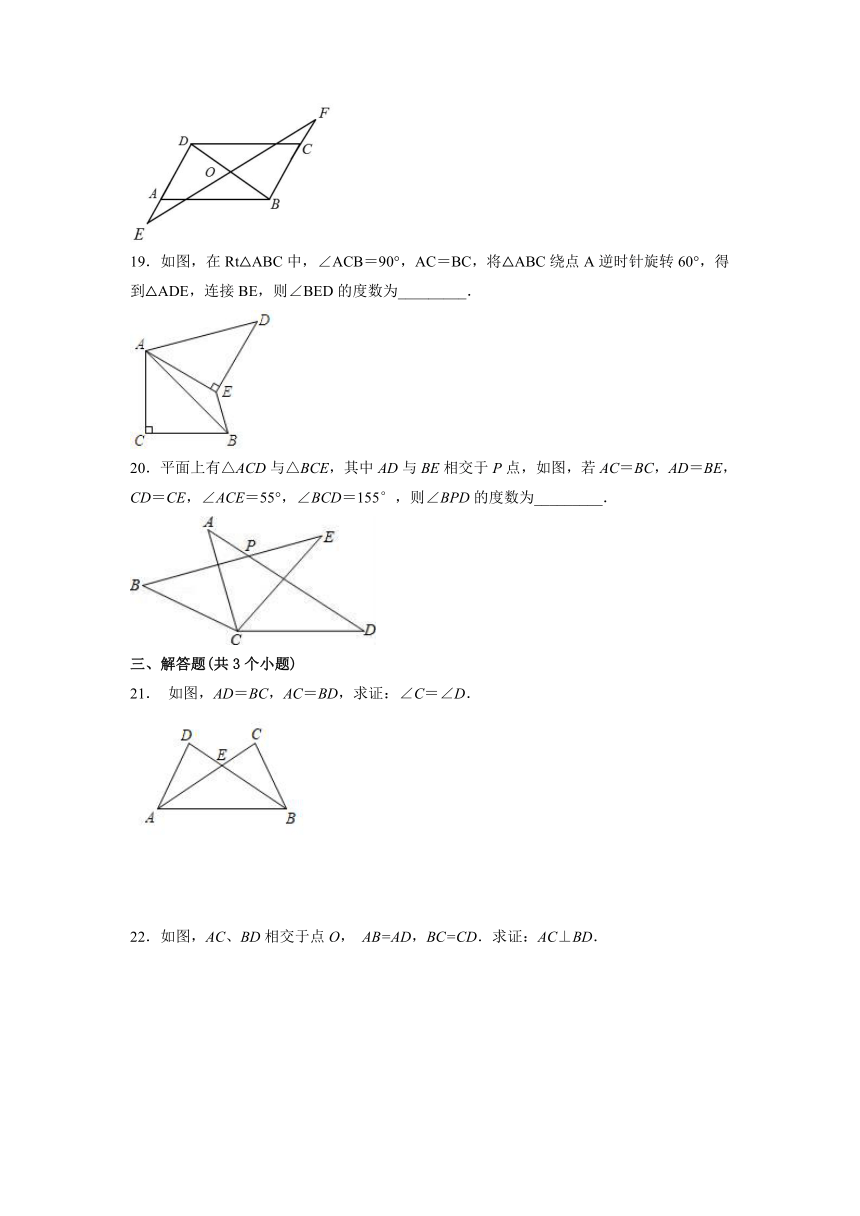
19.如图,在Rt△ABC中,∠ACB=90°,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则∠BED的度数为_________.
20.平面上有△ACD与△BCE,其中AD与BE相交于P点,如图,若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为_________.
三、解答题(共3个小题)
21. 如图,AD=BC,AC=BD,求证:∠C=∠D.
22.如图,AC、BD相交于点O, AB=AD,BC=CD.求证:AC⊥BD.
23.小明和小亮在学习探索三角形全等时,碰到如下一题:如图1,若AC=AD,BC=BD,则△ACB与△ADB有怎样的关系?
(1)请你帮他们解答,并说明理由.
(2)细心的小明在解答的过程中,发现如果在AB上任取一点E,连接CE、DE,则有CE=DE,你知道为什么吗?(如图2)
(3)小亮在小明说出理由后,提出如果在AB的延长线上任取一点P,也有第2题类似的结论.请你帮他画出图形,并证明结论.
13.2.5 边边边解析
1.
【答案】A
【详解】解:在△ABD与△ACD中
∵,
∴△ABD≌△ACD(SSS)
故答案为A.
2.
【答案】B
【详解】解:当BD=CE时,
在△ABD和△ACE中,,
∴△ABD≌△ACE(SSS),
故选:B.
3.
【答案】A
【详解】解:∵,,AD=AD,
∴≌(SSS),
故选:A.
4.
【答案】A
【详解】解:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS).
故选:A.
5.
【答案】C
【详解】解:∵,
∴,即,
∵,
∴.
故选:C
6.
【答案】A
【详解】解:∵AE=FB,
∴AE+BE=FB+BE,
∴AB=FE,
在△ABC和△FED中,
,
∴△ABC≌△FED(SSS),
∵AE=BE和BF=BE推不出AB=FE,
∴可利用的是①或②,
故选:A.
7.
【答案】C
【详解】解:∵BE=DF,
∴BE+EF=DF+EF,
∴BF=DE
又∵AD=BC,AE=CF.
∴△AED≌△CFB(SSS),
∴∠BCF=∠DAE,
∵∠DAE=∠AEB ∠ADB=100°-30°=70°
∴∠BCF=70°.
故选C.
8.
【答案】C
【详解】解:要使△ABP与△ABC全等,点P到AB的距离应该等于点C到AB的距离,即3个单位长度,故点P的位置可以是P1,P3,P4三个,
故选:C.
9.
【答案】C
【详解】解:在与中,
,
,故①正确;
,
在与中,
,
,
,,
,故②正确;
四边形的面积,故③错误;
故选:C.
10.
【答案】C
【详解】,,平分,
,,
;
,,
,,
;
,,,
,,,
;
,,
,
,,
.
综上所述:共有四对全等三角形.
故选:.
11.
【答案】或(填其中任一个均可)
【详解】由题意,有以下两种情况:
(1)当时,由定理可证得;
(2)当时,
,
,即,
则当时,也可利用定理证得;
故答案为:或(填其中任一个均可).
12.
【答案】3
【详解】解:在△AOD与△BOC中,
∴△AOD≌△BOC(SAS);
∴AD=BC,
而OA+OC=OD+OB,即AC=DB,
在△ABD与△BAC中,
∴△ABD≌△BAC(SSS),
在△ADC与△BCD中,
∴△ADC≌△BCD(SSS).
故答案为3.
13.
【答案】3
【详解】∵AB∥DC
∴∠A=∠D
∵AB=CD,AE=DF
∴△ABE≌△DCF(SAS)
∴AE=DF,BE=CF
∴AF=ED
∴△ABF≌△DCE(SAS)
∴BF=EC
∵EF=EF
∴△BEF≌△CFE(SSS)
故答案为:3.
14.
【答案】 SSS ≌
【详解】解:在△ABD与△CBD中,
∴△ABD≌△CBD(SSS),
15.
【答案】3
【详解】解:∵AD=AC,BD=BC,AB=AB,
∴△ADB≌△ACB;
∴∠CAO=∠DAO,∠CBO=∠DBO,
∵AD=AC,BD=BC,OA=OA,OB=OB
∴△ACO≌△ADO,△CBO≌△DBO.
∴图中共有3对全等三角形.
故答案为3.
16.
【答案】50°
【详解】在△ACD和△BCE中,
,
∴△ACD≌△BCE(SSS),
∴∠A=∠B,∠BCE=∠ACD,
∴∠BCA=∠ECD,
∵∠ACE=55°,∠BCD=155°,
∴∠BCA+∠ECD=100°,
∴∠BCA=∠ECD=50°,
∵∠ACE=55°,
∴∠ACD=105°
∴∠A+∠D=75°,
∴∠B+∠D=75°,
∵∠BCD=155°,
∴∠BPD=360°﹣75°﹣155°=130°,
∴∠APB=180°-∠BPD=50°
故答案为:50°.
17.
【答案】47
【详解】解:在△ABC和△ADE中,,
∴(SSS),
∴∠ABC=∠1,∠BAC=∠2,
∴∠3=∠ABC+∠BAC=∠1+∠2,
∵,
∴,
∴.
故答案为:47.
18.
【答案】 60° 10
【详解】解: ,,
O为BD中点,
故答案为:
19.
【答案】135°
【详解】解:如图,连接BD,
∵将△ABC绕点A逆时针旋转60°,得到△ADE,AC=AB
∴AB=AD,∠BAD=60°,AE=DE,∠ADE=45°
∴△ABD为等边三角形,
∴∠ABD=60°,AB=BD,
又∵AE=DE,BE=BE,
∴△ABE≌△DBE(SSS)
∴∠ABE=∠DBE=30°
∴∠ABE=∠DBE=30°,
又∵∠BDE=∠ADB﹣∠ADE=15°,
∴∠BED=135°.
故答案为:135°.
20.
【答案】130°.
【详解】在△ACD和△BCE中,
,
∴△ACD≌△BCE(SSS),
∴∠A=∠B,∠BCE=∠ACD,
∴∠BCA=∠ECD,
∵∠ACE=55°,∠BCD=155°,
∴∠BCA+∠ECD=100°,
∴∠BCA=∠ECD=50°,
∵∠ACE=55°,
∴∠ACD=105°
∴∠A+∠D=75°,
∴∠B+∠D=75°,
∵∠BCD=155°,
∴∠BPD=360°﹣75°﹣155°=130°,
故答案为130°.
21.
【答案】证明见解析
【详解】证明:在△ABD和△BAC中,
∵,
∴△ABD≌△BAC(SSS),
∴∠C=∠D.
22.
【答案】见解析
【详解】∵ 在△ ABC和△ ADC中
∴ △ ABC≌△ ADC(SSS)
∴ ∠ BAC=∠ DAC
∵ 在△ABO和△ADO中
∴ △ ABO≌△ ADO(SAS)
∴ ∠AOB=∠AOD
又∵∠AOB+∠AOD=180°
∴ ∠AOB=90°
∴ AC⊥BD
23.
【答案】(1),理由见解析;(2)见解析;(3)见解析
【详解】解:(1),理由如下:
如图1,在与中,
,
;
(2)如图2,由(1)知,,则.
在与中,
,
,
;
(3)如图3,.
理由同(2),,则.
一、单选题(共10个小题)
1.如图,AB=AC,DB=DC则直接由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△EBD≌△ECD D.以上答案都不对
2.如图,已知AB=AC,AE=AD,要利用“SSS”推理得出△ABD≌△ACE,还需要添加的一个条件是( )
A.∠B=∠C B.BD=CE C.∠BAD=∠CAE D.以上都不对
3.如下图,在和中,,,则能说明≌的依据是( )
A.SSS B.ASA C.AAS D.SAS
4.如图,这是一个平分角的仪器,,将点A放在一个角的顶点,使AB、AD分别与这个角的两边重合,可证,从而得到AC就是这个角的平分线.其中证明的数学依据是( )
A.SSS B.ASA C.SAS D.AAS
5.如图,已知,则的理由是( )
A. B. C. D.
6.如图,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或② B.②或③ C.①或③ D.①或④
7.如图,AD=BC,AE=CF.E、F是BD上两点,BE=DF,∠AEB=100°,∠ADB=30°,则∠BCF的度数为( )
A.30° B.60° C.70° D.80°
8.如图,在方格纸中,以为一边作,使之与全等,从,,,四个点中找出符合条件的点,则点有( )
A.个 B.个 C.个 D.个
9.两组邻边分别相等的四边形叫做“筝形”,如图,四边形是一个筝形,其中,,在探究筝形的性质时,得到如下结论:①;②;③四边形的面积,其中正确的结论有( )
A.个 B.个 C.个 D.个
10.如图,已知,,且平分,那么图中全等三角形共有
A.2对 B.3对 C.4对 D.5对
二、填空题(共10个小题)
11.如图,AB=AC,BE=CD,要使,依据SSS,则还需添加条件_______________.(填一个即可)
12.如图,AC、BD相交于点O,OA=OB,OC=OD,则图中全等三角形共有______对.
13.如图,点,在线段上,且,,,连接,,,,则图中共有_______对全等三角形.
14.如图,AB=CB,AD=CD 根据__________可得到△ABD_______△CBD.
15.已知,如图,AD=AC,BD=BC,O为AB上一点,那么图中共有_______对全等三角形.
16.如图,在△ACD与△BCE中,AD与BE相交于点P,若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠APB的度数为__________.
17.如图,点B、C、E三点在同一直线上,且AB=AD,AC=AE,BC=DE,若,则∠3=________°.
18.如图,,,O为BD中点,过O点作直线与DA、BC延长线交于E,F,若,,则_________,_________.
19.如图,在Rt△ABC中,∠ACB=90°,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则∠BED的度数为_________.
20.平面上有△ACD与△BCE,其中AD与BE相交于P点,如图,若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为_________.
三、解答题(共3个小题)
21. 如图,AD=BC,AC=BD,求证:∠C=∠D.
22.如图,AC、BD相交于点O, AB=AD,BC=CD.求证:AC⊥BD.
23.小明和小亮在学习探索三角形全等时,碰到如下一题:如图1,若AC=AD,BC=BD,则△ACB与△ADB有怎样的关系?
(1)请你帮他们解答,并说明理由.
(2)细心的小明在解答的过程中,发现如果在AB上任取一点E,连接CE、DE,则有CE=DE,你知道为什么吗?(如图2)
(3)小亮在小明说出理由后,提出如果在AB的延长线上任取一点P,也有第2题类似的结论.请你帮他画出图形,并证明结论.
13.2.5 边边边解析
1.
【答案】A
【详解】解:在△ABD与△ACD中
∵,
∴△ABD≌△ACD(SSS)
故答案为A.
2.
【答案】B
【详解】解:当BD=CE时,
在△ABD和△ACE中,,
∴△ABD≌△ACE(SSS),
故选:B.
3.
【答案】A
【详解】解:∵,,AD=AD,
∴≌(SSS),
故选:A.
4.
【答案】A
【详解】解:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS).
故选:A.
5.
【答案】C
【详解】解:∵,
∴,即,
∵,
∴.
故选:C
6.
【答案】A
【详解】解:∵AE=FB,
∴AE+BE=FB+BE,
∴AB=FE,
在△ABC和△FED中,
,
∴△ABC≌△FED(SSS),
∵AE=BE和BF=BE推不出AB=FE,
∴可利用的是①或②,
故选:A.
7.
【答案】C
【详解】解:∵BE=DF,
∴BE+EF=DF+EF,
∴BF=DE
又∵AD=BC,AE=CF.
∴△AED≌△CFB(SSS),
∴∠BCF=∠DAE,
∵∠DAE=∠AEB ∠ADB=100°-30°=70°
∴∠BCF=70°.
故选C.
8.
【答案】C
【详解】解:要使△ABP与△ABC全等,点P到AB的距离应该等于点C到AB的距离,即3个单位长度,故点P的位置可以是P1,P3,P4三个,
故选:C.
9.
【答案】C
【详解】解:在与中,
,
,故①正确;
,
在与中,
,
,
,,
,故②正确;
四边形的面积,故③错误;
故选:C.
10.
【答案】C
【详解】,,平分,
,,
;
,,
,,
;
,,,
,,,
;
,,
,
,,
.
综上所述:共有四对全等三角形.
故选:.
11.
【答案】或(填其中任一个均可)
【详解】由题意,有以下两种情况:
(1)当时,由定理可证得;
(2)当时,
,
,即,
则当时,也可利用定理证得;
故答案为:或(填其中任一个均可).
12.
【答案】3
【详解】解:在△AOD与△BOC中,
∴△AOD≌△BOC(SAS);
∴AD=BC,
而OA+OC=OD+OB,即AC=DB,
在△ABD与△BAC中,
∴△ABD≌△BAC(SSS),
在△ADC与△BCD中,
∴△ADC≌△BCD(SSS).
故答案为3.
13.
【答案】3
【详解】∵AB∥DC
∴∠A=∠D
∵AB=CD,AE=DF
∴△ABE≌△DCF(SAS)
∴AE=DF,BE=CF
∴AF=ED
∴△ABF≌△DCE(SAS)
∴BF=EC
∵EF=EF
∴△BEF≌△CFE(SSS)
故答案为:3.
14.
【答案】 SSS ≌
【详解】解:在△ABD与△CBD中,
∴△ABD≌△CBD(SSS),
15.
【答案】3
【详解】解:∵AD=AC,BD=BC,AB=AB,
∴△ADB≌△ACB;
∴∠CAO=∠DAO,∠CBO=∠DBO,
∵AD=AC,BD=BC,OA=OA,OB=OB
∴△ACO≌△ADO,△CBO≌△DBO.
∴图中共有3对全等三角形.
故答案为3.
16.
【答案】50°
【详解】在△ACD和△BCE中,
,
∴△ACD≌△BCE(SSS),
∴∠A=∠B,∠BCE=∠ACD,
∴∠BCA=∠ECD,
∵∠ACE=55°,∠BCD=155°,
∴∠BCA+∠ECD=100°,
∴∠BCA=∠ECD=50°,
∵∠ACE=55°,
∴∠ACD=105°
∴∠A+∠D=75°,
∴∠B+∠D=75°,
∵∠BCD=155°,
∴∠BPD=360°﹣75°﹣155°=130°,
∴∠APB=180°-∠BPD=50°
故答案为:50°.
17.
【答案】47
【详解】解:在△ABC和△ADE中,,
∴(SSS),
∴∠ABC=∠1,∠BAC=∠2,
∴∠3=∠ABC+∠BAC=∠1+∠2,
∵,
∴,
∴.
故答案为:47.
18.
【答案】 60° 10
【详解】解: ,,
O为BD中点,
故答案为:
19.
【答案】135°
【详解】解:如图,连接BD,
∵将△ABC绕点A逆时针旋转60°,得到△ADE,AC=AB
∴AB=AD,∠BAD=60°,AE=DE,∠ADE=45°
∴△ABD为等边三角形,
∴∠ABD=60°,AB=BD,
又∵AE=DE,BE=BE,
∴△ABE≌△DBE(SSS)
∴∠ABE=∠DBE=30°
∴∠ABE=∠DBE=30°,
又∵∠BDE=∠ADB﹣∠ADE=15°,
∴∠BED=135°.
故答案为:135°.
20.
【答案】130°.
【详解】在△ACD和△BCE中,
,
∴△ACD≌△BCE(SSS),
∴∠A=∠B,∠BCE=∠ACD,
∴∠BCA=∠ECD,
∵∠ACE=55°,∠BCD=155°,
∴∠BCA+∠ECD=100°,
∴∠BCA=∠ECD=50°,
∵∠ACE=55°,
∴∠ACD=105°
∴∠A+∠D=75°,
∴∠B+∠D=75°,
∵∠BCD=155°,
∴∠BPD=360°﹣75°﹣155°=130°,
故答案为130°.
21.
【答案】证明见解析
【详解】证明:在△ABD和△BAC中,
∵,
∴△ABD≌△BAC(SSS),
∴∠C=∠D.
22.
【答案】见解析
【详解】∵ 在△ ABC和△ ADC中
∴ △ ABC≌△ ADC(SSS)
∴ ∠ BAC=∠ DAC
∵ 在△ABO和△ADO中
∴ △ ABO≌△ ADO(SAS)
∴ ∠AOB=∠AOD
又∵∠AOB+∠AOD=180°
∴ ∠AOB=90°
∴ AC⊥BD
23.
【答案】(1),理由见解析;(2)见解析;(3)见解析
【详解】解:(1),理由如下:
如图1,在与中,
,
;
(2)如图2,由(1)知,,则.
在与中,
,
,
;
(3)如图3,.
理由同(2),,则.
