2022-2023学年 华东师大版八年级数学上册 13.2.6 斜边直角边 课时练习 (含答案)
文档属性
| 名称 | 2022-2023学年 华东师大版八年级数学上册 13.2.6 斜边直角边 课时练习 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-16 16:47:53 | ||
图片预览


文档简介
13.2.6 斜边直角边(附解析)
一、单选题(共10个小题)
1.如图,已知,,.则的理由是( )
A.HL B.SAS C.AAS D.ASA
2.如图,在的两边上,分别取,再分别过点、作、的垂线,交点为,画射线.可判定,依据是( )
A.ASA B.SAS C.AAS D.HL
3.已知:如图,在△ABC中,点D在边BC上,DB=DC,,,垂足分别为E,F,DE=DF.
求证:.以下是排乱的证明过程:
①∴∠BED=∠CFD=90°,
②∴.
③∵DE⊥AB,DF⊥AC,
④∵在和中,,
证明步骤正确的顺序是( )
A.③→②→①→④ B.③→①→④→②
C.①→②→④→③ D.①→④→③→②
4.下列关于两个直角三角形全等的判定,不正确的是( )
A.斜边和一锐角分别相等的两个直角三角形全等
B.两条直角边分别相等的两个直角三角形全等
C.斜边和一条直角边分别相等的两个直角三角形全等
D.两个面积相等的直角三角形全等
5.如图,CD⊥AD于点D,CB⊥AB于点B,CD=CB,那么可以直接判定△ADC≌△ABC的定理是( )
A.AAS B.SAS C.SSS D.HL
6.如图,点B、F、C、E在一条直线上,∠A=∠D=90°,AB=DE,添加下列选项中的条件,能用HL判定△ABC≌△DEF的是( )
A.AC=DF B.∠B=∠E C.∠ACB=∠DFE D.BC=EF
7.如图,已知点A、D、C、F在同一条直线上,∠B=∠E =90°,AB=DE,若添加一个条件后,能用“HL”的方法判定Rt△ABC≌Rt△DEF,添加的条件可以是( )
A.BC=EF B.∠BCA=∠F C.AB∥DE D.AD=CF
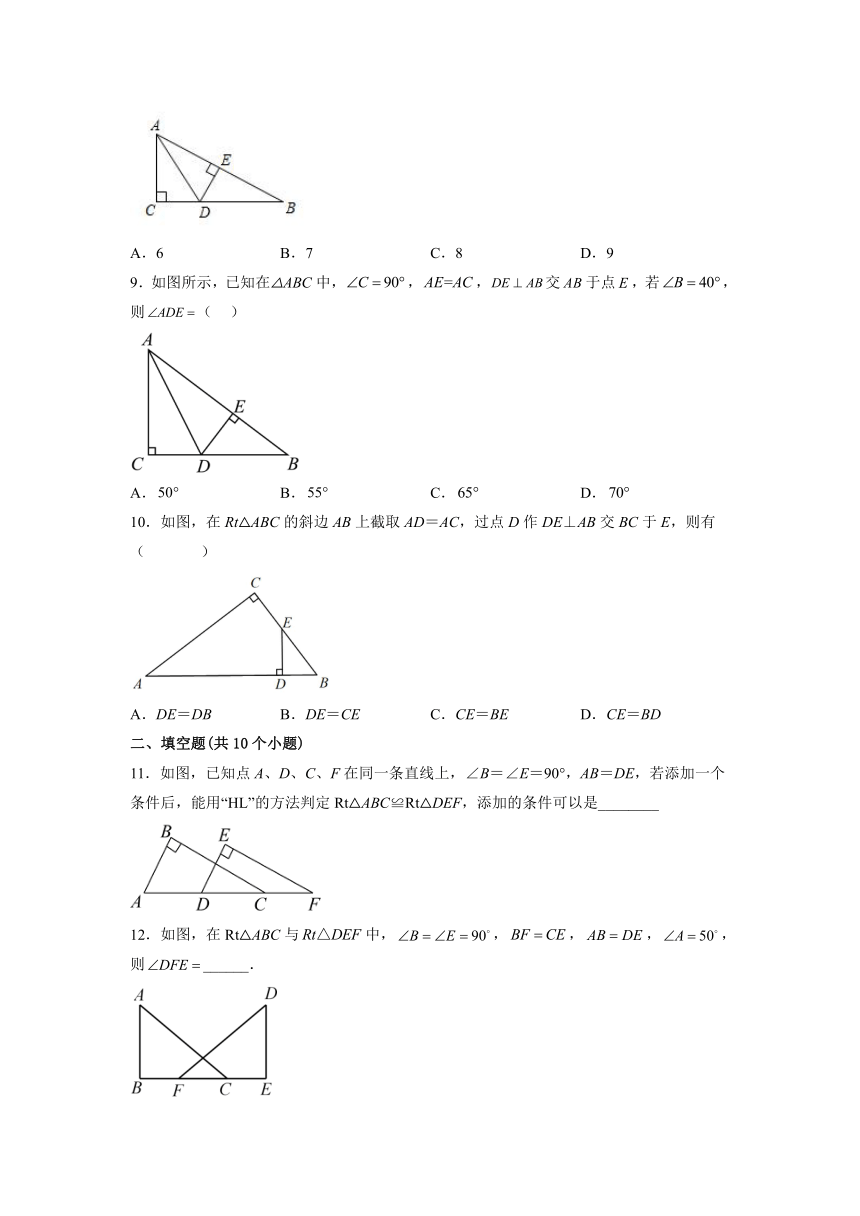
8.如图,在△ABC中,,D是上一点,于点E,,连接,若,则等于( )
A.6 B.7 C.8 D.9
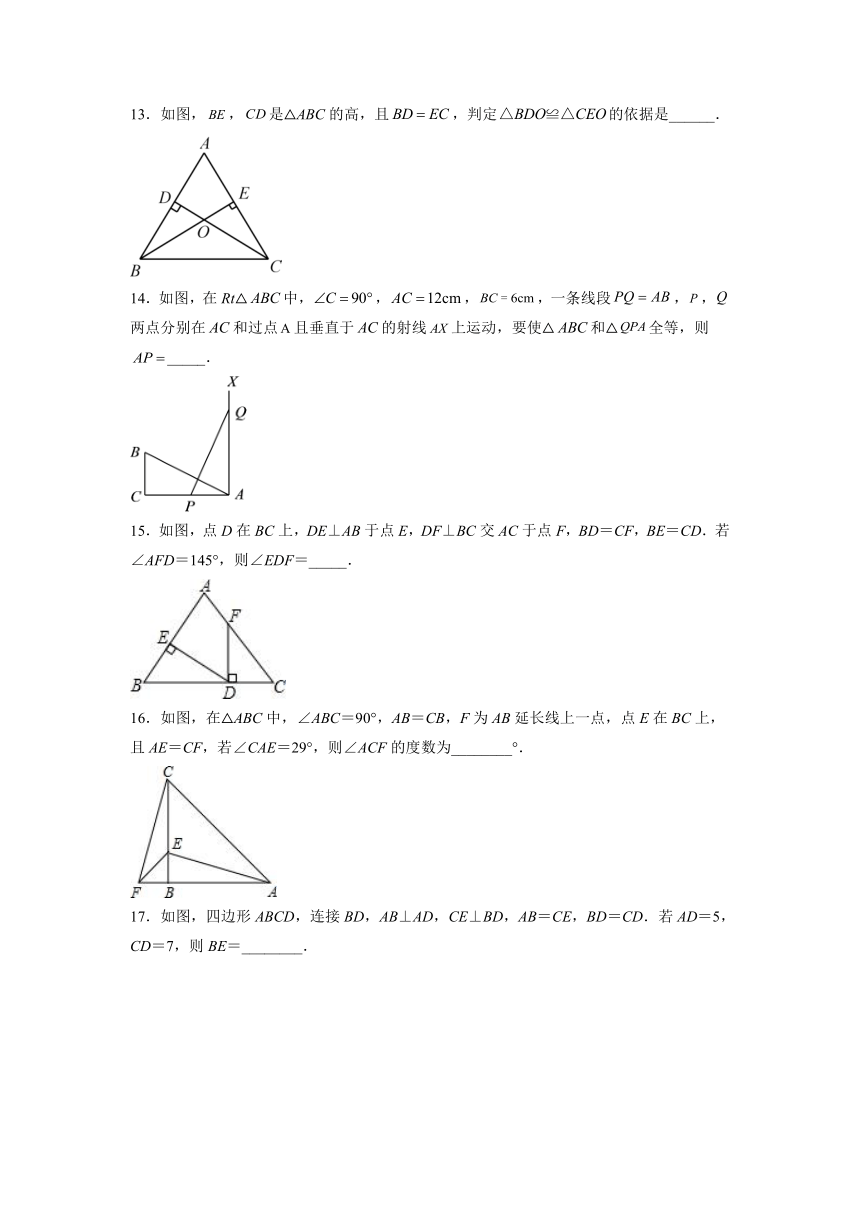
9.如图所示,已知在△ABC中,,,交于点,若,则( )
A. B. C. D.
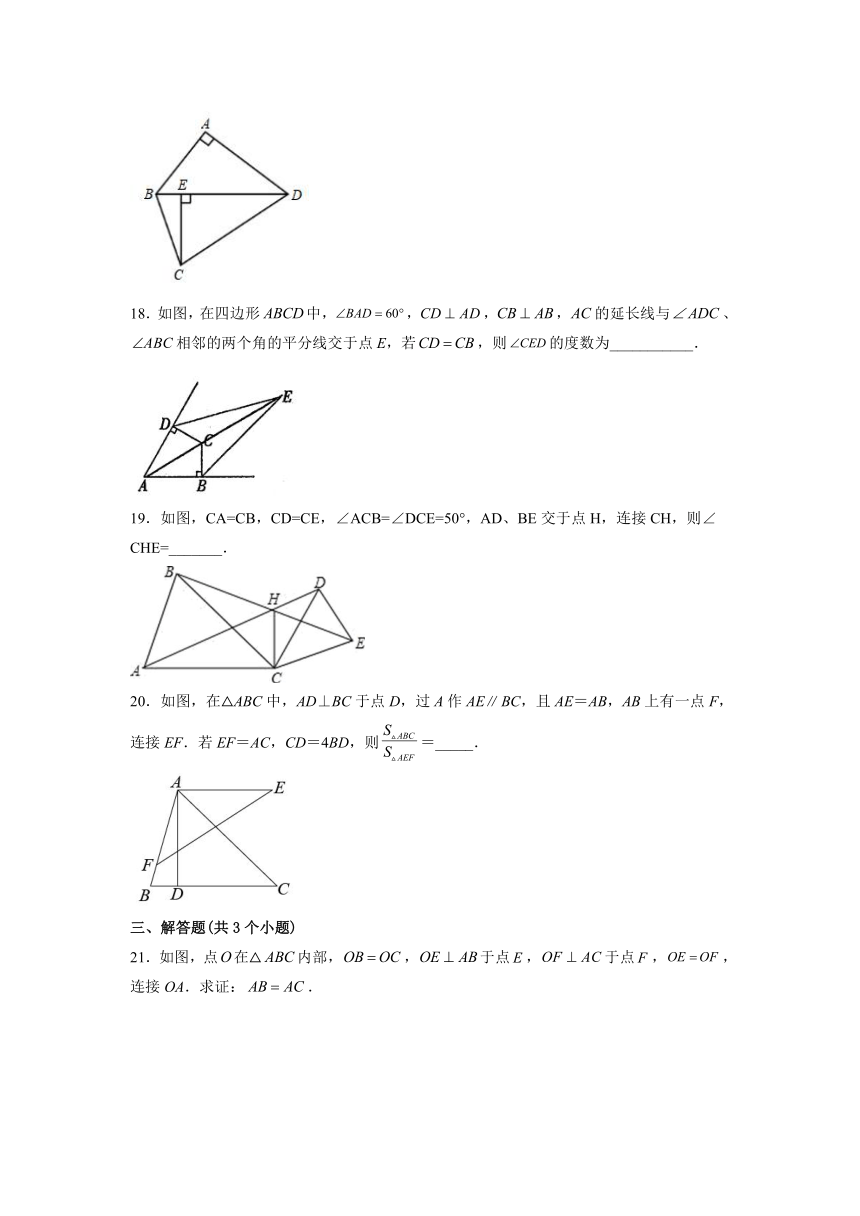
10.如图,在Rt△ABC的斜边AB上截取AD=AC,过点D作DE⊥AB交BC于E,则有( )
A.DE=DB B.DE=CE C.CE=BE D.CE=BD
二、填空题(共10个小题)
11.如图,已知点A、D、C、F在同一条直线上,∠B=∠E=90°,AB=DE,若添加一个条件后,能用“HL”的方法判定Rt△ABC≌Rt△DEF,添加的条件可以是________
12.如图,在Rt△ABC与中,,,,,则______.
13.如图,,是△ABC的高,且,判定的依据是______.
14.如图,在Rt△中,,,,一条线段,,两点分别在和过点且垂直于的射线上运动,要使△和△全等,则_____.
15.如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=_____.
16.如图,在△ABC中,∠ABC=90°,AB=CB,F为AB延长线上一点,点E在BC上,且AE=CF,若∠CAE=29°,则∠ACF的度数为________°.
17.如图,四边形ABCD,连接BD,AB⊥AD,CE⊥BD,AB=CE,BD=CD.若AD=5,CD=7,则BE=________.
18.如图,在四边形中,,,,的延长线与、相邻的两个角的平分线交于点E,若,则的度数为___________.
19.如图,CA=CB,CD=CE,∠ACB=∠DCE=50°,AD、BE交于点H,连接CH,则∠CHE=_______.
20.如图,在△ABC中,AD⊥BC于点D,过A作AEBC,且AE=AB,AB上有一点F,连接EF.若EF=AC,CD=4BD,则=_____.
三、解答题(共3个小题)
21.如图,点在△内部,,于点,于点,,连接OA.求证:.
22.如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图1所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图2所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
23.将两个全等的直角三角形△ABC和△DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)求证:AF+EF=DE;
(2)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图②.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由;
(3)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图③中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立.
13.2.6 斜边直角边解析
1.
【答案】A
【详解】证明:∵AD⊥BD,BC⊥AC,
∴∠C=∠D=90°,
在Rt△CAB和Rt△DBA中,
,
∴Rt△CAB≌Rt△DBA(HL).
故选:A.
2.
【答案】D
【详解】解:由题意可知,和都是直角三角形,
在和中,
,
满足斜边相等和一组直角边相等,
因此,
故选D.
3.
【答案】B
【详解】证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
在Rt△DEB和Rt△DFC中,
,
∴Rt△DEB≌Rt△DFC(HL),
即选项B正确;选项A、选项C、选项D都错误;
故选:B.
4.
【答案】D
【详解】解:A、利用AAS来判定全等,不符合题意;
B、利用SAS来判定全等,不符合题意;
C、利用HL来判定全等,不符合题意;
D、面积相等不一定能推出两直角三角形全等,没有相关判定方法对应,符合题意.
故选:D.
5.
【答案】D
【详解】解:∵CD⊥AD于点D,CB⊥AB于点B,
∴∠CDA=∠CBA=90°
在直角△CDA与直角△CBA中,
∴(HL)
故选:D.
6.
【答案】D
【详解】解:A、添加,需用定理判定,则此项不符题意;
B、添加,需用定理判定,则此项不符题意;
C、添加,需用定理判定,则此项不符题意;
D、添加,能用定理判定,则此项符合题意;
故选:D.
7.
【答案】D
【详解】解:∵,,
∴添加条件,根据“HL”即可判定≌;或添加条件,也可得出,根据“HL”即可判定≌,故D正确.
故选:D.
8.
【答案】C
【详解】解:∵DE⊥AB,
∴∠DEB=90°,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴CD=DE,
∴BD+DE=BD+CD=BC,
∵BC=8,
∴BD+DE=BC=8.
故选:C.
9.
【答案】C
【详解】解:∵,
∴,
在和中,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
故选:C
10.
【答案】B
【详解】解:如图,连接AE,
∵DE⊥AB,
∴∠ADE=∠C=90°,
在Rt△ACE和Rt△ADE中,
∵AE=AE,AC=AD,
∴Rt△ACE≌Rt△ADE(HL),
∴DE=CE.
故选:B
11.
【答案】AD=CF或AC=DF
【详解】解∶当AC=DF时,
∵Rt△ABC和Rt△DEF中,
,
∴(HL);
当AD=CF时,
∵AD=CF,
∴AD+CD=CF+CD即AC=DF,由得(HL);
∴当添加AD=CF或AC= DF时,根据“HL”可判定Rt△ABC≌Rt△DEF .
故答案为∶ AD=CF (或AC=DF ) .
12.
【答案】40°
【详解】解:在Rt△ABC中,
,
∴Rt△ABC
∴,
∵,
∴,
故答案为:40°
13.
【答案】HL
【详解】解:∵BE、CD是△ABC的高,
∴∠BDC=∠BEC=90°
在Rt△BDC和Rt△BEC中:
BD=EC,BC=CB
∴△BCD≌△CBE(HL).
故答案为:HL.
14.
【答案】12cm或6cm
【详解】解:∵∠C=90°,AO⊥AC,
∴∠C=∠QAP=90°,
①当AP=6cm=BC时,
在Rt△ACB和Rt△QAP中
∵,
∴Rt△ACB≌Rt△QAP(HL),
②当AP=12cm=AC时,
在Rt△ACB和Rt△PAQ中
,
∴Rt△ACB≌Rt△PAQ(HL),
故答案为:12cm或6cm.
15.
【答案】55°
【详解】解:∵∠DFC+∠AFD=180°,∠AFD=145°,
∴∠CFD=35°.
又∵DE⊥AB,DF⊥BC,
∴∠BED=∠CDF=90°,
在Rt△BDE与△Rt△CFD中,
,
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=35°,
∴∠EDF+∠BDE=∠EDF+∠CFD=90°,
∴∠EDF=55°.
故答案是:55°.
16.
【答案】61
【详解】解:∵在△ABC中,∠ABC=90°,AB=CB,
∴∠BAC=∠BCA=45°,
∵∠CAE=29°,
∴∠BAE=16°,
在Rt△ABE和Rt△CBF中,,
∴Rt△ABE≌Rt△CBF(HL),
∴∠BAE=∠BCF=16°,
∴∠ACF=∠BCA+∠BCF=61°,
故答案为:61.
17.
【答案】2
【详解】解: AB⊥AD,CE⊥BD,
,
在与中,
,
,
AD=5,CD=7,
,BD=CD=7,
故答案为:2
18.
【答案】
【详解】解:∵,,
∴∠CDA=∠CBA=90°,
在Rt△CDA和Rt△CBA中,
,
∴Rt△CDA≌Rt△CBA(HL),
∴,
∵DE平分与∠ADC相邻的角,∠ADC=90°,
∴∠EDC=45°,
∴∠CED=180°-∠DAE-∠ADC-∠EDC=15°,
故答案为:15°.
19.
【答案】65°
【详解】解:如图,,
,
在和中,
;
过点作于,于,
,
,
在和中,
,
,
在与中
,
,
平分;
,
,
,
,
,
,
故答案为:.
20.
【答案】
【详解】解:如图,在CD上取一点G,使GD=BD,连接AG,作EH⊥AB交BA的延长线于点H,
∵AD⊥BC于点D,
∴AG=AB,∠H=∠ADG=90°
∴∠AGD=∠B,
∵AE//BC,
∴∠EAH=∠B,
∴∠EAH=∠AGD,
∵AE=AB,
∴AE=AG,
在△AEH和△GAD中,
,
∴△AEH≌△GAD(AAS),
∴EH=AD,AH=GD,
在Rt△EHF和Rt△ADC中,
,
∴Rt△EHF≌Rt△ADC(HL),
∴FH=CD,
∴FH-AH=CD-GD,
∴AF=GC,
∴,
∴S△AEF=S△GAC,
设GD=BD=m,则CD=4BD=4m,
∴CG=4m-m=3m,BC=4m+m=5m,
∴,
∴,
故答案为:.
21.
【答案】证明见解析
【详解】证明:∵,,
∴,
在Rt△AEO和中,
,
∴Rt△AEO≌Rt△AFO (HL),
∴,
在Rt△BEO和Rt△CFO中,
,
∴Rt△BEO≌Rt△CFO (HL),
∴,
∴,
∴.
22.
【答案】(1)见解析;(2)AB⊥AC,见解析
【详解】(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
在Rt△ABD和Rt△ACE中,
∵,
∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC.
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.
∠BAC=180°﹣(∠BAD+∠CAE)=90°.
∴AB⊥AC.
(2)AB⊥AC.理由如下:
同(1)一样可证得Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90°,即∠BAC=90°,
∴AB⊥AC.
23.
【答案】(1)证明见详解;(2)AF=DE+EF,理由见详解;(3)成立,理由见详解.
【详解】解:(1)证明:连接BF,如图,
∵△ABC≌△DBE(已知),
∴BC=BE,AC=DE.
∵∠ACB=∠DEB=90°,
∴∠BCF=∠BEF=90°.
在Rt△BFC和Rt△BFE中,
∴Rt△BFC≌Rt△BFE(HL).
∴CF=EF.
又∵AF+CF=AC,
∴AF+EF=DE.
(2)证明:连接BF,
∵△ABC≌△DBE,
∴BC=BE,
∵∠ACB=∠DEB=90°,
∴△BCF和△BEF是直角三角形,
在Rt△BCF和Rt△BEF中,
,
∴△BCF≌△BEF(HL),
∴CF=EF;
∵△ABC≌△DBE,
∴AC=DE,
∴AF=AC+FC=DE+EF.
(3)画出正确图形如图:
同(1)得CF=EF,
∵△ABC≌△DBE,
∴AC=DE,
∴AF+FC=AF+EF=AC=DE.
∴(1)中的结论AF+EF=DE仍然成立;
一、单选题(共10个小题)
1.如图,已知,,.则的理由是( )
A.HL B.SAS C.AAS D.ASA
2.如图,在的两边上,分别取,再分别过点、作、的垂线,交点为,画射线.可判定,依据是( )
A.ASA B.SAS C.AAS D.HL
3.已知:如图,在△ABC中,点D在边BC上,DB=DC,,,垂足分别为E,F,DE=DF.
求证:.以下是排乱的证明过程:
①∴∠BED=∠CFD=90°,
②∴.
③∵DE⊥AB,DF⊥AC,
④∵在和中,,
证明步骤正确的顺序是( )
A.③→②→①→④ B.③→①→④→②
C.①→②→④→③ D.①→④→③→②
4.下列关于两个直角三角形全等的判定,不正确的是( )
A.斜边和一锐角分别相等的两个直角三角形全等
B.两条直角边分别相等的两个直角三角形全等
C.斜边和一条直角边分别相等的两个直角三角形全等
D.两个面积相等的直角三角形全等
5.如图,CD⊥AD于点D,CB⊥AB于点B,CD=CB,那么可以直接判定△ADC≌△ABC的定理是( )
A.AAS B.SAS C.SSS D.HL
6.如图,点B、F、C、E在一条直线上,∠A=∠D=90°,AB=DE,添加下列选项中的条件,能用HL判定△ABC≌△DEF的是( )
A.AC=DF B.∠B=∠E C.∠ACB=∠DFE D.BC=EF
7.如图,已知点A、D、C、F在同一条直线上,∠B=∠E =90°,AB=DE,若添加一个条件后,能用“HL”的方法判定Rt△ABC≌Rt△DEF,添加的条件可以是( )
A.BC=EF B.∠BCA=∠F C.AB∥DE D.AD=CF
8.如图,在△ABC中,,D是上一点,于点E,,连接,若,则等于( )
A.6 B.7 C.8 D.9
9.如图所示,已知在△ABC中,,,交于点,若,则( )
A. B. C. D.
10.如图,在Rt△ABC的斜边AB上截取AD=AC,过点D作DE⊥AB交BC于E,则有( )
A.DE=DB B.DE=CE C.CE=BE D.CE=BD
二、填空题(共10个小题)
11.如图,已知点A、D、C、F在同一条直线上,∠B=∠E=90°,AB=DE,若添加一个条件后,能用“HL”的方法判定Rt△ABC≌Rt△DEF,添加的条件可以是________
12.如图,在Rt△ABC与中,,,,,则______.
13.如图,,是△ABC的高,且,判定的依据是______.
14.如图,在Rt△中,,,,一条线段,,两点分别在和过点且垂直于的射线上运动,要使△和△全等,则_____.
15.如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=_____.
16.如图,在△ABC中,∠ABC=90°,AB=CB,F为AB延长线上一点,点E在BC上,且AE=CF,若∠CAE=29°,则∠ACF的度数为________°.
17.如图,四边形ABCD,连接BD,AB⊥AD,CE⊥BD,AB=CE,BD=CD.若AD=5,CD=7,则BE=________.
18.如图,在四边形中,,,,的延长线与、相邻的两个角的平分线交于点E,若,则的度数为___________.
19.如图,CA=CB,CD=CE,∠ACB=∠DCE=50°,AD、BE交于点H,连接CH,则∠CHE=_______.
20.如图,在△ABC中,AD⊥BC于点D,过A作AEBC,且AE=AB,AB上有一点F,连接EF.若EF=AC,CD=4BD,则=_____.
三、解答题(共3个小题)
21.如图,点在△内部,,于点,于点,,连接OA.求证:.
22.如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图1所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图2所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
23.将两个全等的直角三角形△ABC和△DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)求证:AF+EF=DE;
(2)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图②.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由;
(3)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图③中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立.
13.2.6 斜边直角边解析
1.
【答案】A
【详解】证明:∵AD⊥BD,BC⊥AC,
∴∠C=∠D=90°,
在Rt△CAB和Rt△DBA中,
,
∴Rt△CAB≌Rt△DBA(HL).
故选:A.
2.
【答案】D
【详解】解:由题意可知,和都是直角三角形,
在和中,
,
满足斜边相等和一组直角边相等,
因此,
故选D.
3.
【答案】B
【详解】证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
在Rt△DEB和Rt△DFC中,
,
∴Rt△DEB≌Rt△DFC(HL),
即选项B正确;选项A、选项C、选项D都错误;
故选:B.
4.
【答案】D
【详解】解:A、利用AAS来判定全等,不符合题意;
B、利用SAS来判定全等,不符合题意;
C、利用HL来判定全等,不符合题意;
D、面积相等不一定能推出两直角三角形全等,没有相关判定方法对应,符合题意.
故选:D.
5.
【答案】D
【详解】解:∵CD⊥AD于点D,CB⊥AB于点B,
∴∠CDA=∠CBA=90°
在直角△CDA与直角△CBA中,
∴(HL)
故选:D.
6.
【答案】D
【详解】解:A、添加,需用定理判定,则此项不符题意;
B、添加,需用定理判定,则此项不符题意;
C、添加,需用定理判定,则此项不符题意;
D、添加,能用定理判定,则此项符合题意;
故选:D.
7.
【答案】D
【详解】解:∵,,
∴添加条件,根据“HL”即可判定≌;或添加条件,也可得出,根据“HL”即可判定≌,故D正确.
故选:D.
8.
【答案】C
【详解】解:∵DE⊥AB,
∴∠DEB=90°,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴CD=DE,
∴BD+DE=BD+CD=BC,
∵BC=8,
∴BD+DE=BC=8.
故选:C.
9.
【答案】C
【详解】解:∵,
∴,
在和中,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
故选:C
10.
【答案】B
【详解】解:如图,连接AE,
∵DE⊥AB,
∴∠ADE=∠C=90°,
在Rt△ACE和Rt△ADE中,
∵AE=AE,AC=AD,
∴Rt△ACE≌Rt△ADE(HL),
∴DE=CE.
故选:B
11.
【答案】AD=CF或AC=DF
【详解】解∶当AC=DF时,
∵Rt△ABC和Rt△DEF中,
,
∴(HL);
当AD=CF时,
∵AD=CF,
∴AD+CD=CF+CD即AC=DF,由得(HL);
∴当添加AD=CF或AC= DF时,根据“HL”可判定Rt△ABC≌Rt△DEF .
故答案为∶ AD=CF (或AC=DF ) .
12.
【答案】40°
【详解】解:在Rt△ABC中,
,
∴Rt△ABC
∴,
∵,
∴,
故答案为:40°
13.
【答案】HL
【详解】解:∵BE、CD是△ABC的高,
∴∠BDC=∠BEC=90°
在Rt△BDC和Rt△BEC中:
BD=EC,BC=CB
∴△BCD≌△CBE(HL).
故答案为:HL.
14.
【答案】12cm或6cm
【详解】解:∵∠C=90°,AO⊥AC,
∴∠C=∠QAP=90°,
①当AP=6cm=BC时,
在Rt△ACB和Rt△QAP中
∵,
∴Rt△ACB≌Rt△QAP(HL),
②当AP=12cm=AC时,
在Rt△ACB和Rt△PAQ中
,
∴Rt△ACB≌Rt△PAQ(HL),
故答案为:12cm或6cm.
15.
【答案】55°
【详解】解:∵∠DFC+∠AFD=180°,∠AFD=145°,
∴∠CFD=35°.
又∵DE⊥AB,DF⊥BC,
∴∠BED=∠CDF=90°,
在Rt△BDE与△Rt△CFD中,
,
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=35°,
∴∠EDF+∠BDE=∠EDF+∠CFD=90°,
∴∠EDF=55°.
故答案是:55°.
16.
【答案】61
【详解】解:∵在△ABC中,∠ABC=90°,AB=CB,
∴∠BAC=∠BCA=45°,
∵∠CAE=29°,
∴∠BAE=16°,
在Rt△ABE和Rt△CBF中,,
∴Rt△ABE≌Rt△CBF(HL),
∴∠BAE=∠BCF=16°,
∴∠ACF=∠BCA+∠BCF=61°,
故答案为:61.
17.
【答案】2
【详解】解: AB⊥AD,CE⊥BD,
,
在与中,
,
,
AD=5,CD=7,
,BD=CD=7,
故答案为:2
18.
【答案】
【详解】解:∵,,
∴∠CDA=∠CBA=90°,
在Rt△CDA和Rt△CBA中,
,
∴Rt△CDA≌Rt△CBA(HL),
∴,
∵DE平分与∠ADC相邻的角,∠ADC=90°,
∴∠EDC=45°,
∴∠CED=180°-∠DAE-∠ADC-∠EDC=15°,
故答案为:15°.
19.
【答案】65°
【详解】解:如图,,
,
在和中,
;
过点作于,于,
,
,
在和中,
,
,
在与中
,
,
平分;
,
,
,
,
,
,
故答案为:.
20.
【答案】
【详解】解:如图,在CD上取一点G,使GD=BD,连接AG,作EH⊥AB交BA的延长线于点H,
∵AD⊥BC于点D,
∴AG=AB,∠H=∠ADG=90°
∴∠AGD=∠B,
∵AE//BC,
∴∠EAH=∠B,
∴∠EAH=∠AGD,
∵AE=AB,
∴AE=AG,
在△AEH和△GAD中,
,
∴△AEH≌△GAD(AAS),
∴EH=AD,AH=GD,
在Rt△EHF和Rt△ADC中,
,
∴Rt△EHF≌Rt△ADC(HL),
∴FH=CD,
∴FH-AH=CD-GD,
∴AF=GC,
∴,
∴S△AEF=S△GAC,
设GD=BD=m,则CD=4BD=4m,
∴CG=4m-m=3m,BC=4m+m=5m,
∴,
∴,
故答案为:.
21.
【答案】证明见解析
【详解】证明:∵,,
∴,
在Rt△AEO和中,
,
∴Rt△AEO≌Rt△AFO (HL),
∴,
在Rt△BEO和Rt△CFO中,
,
∴Rt△BEO≌Rt△CFO (HL),
∴,
∴,
∴.
22.
【答案】(1)见解析;(2)AB⊥AC,见解析
【详解】(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
在Rt△ABD和Rt△ACE中,
∵,
∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC.
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.
∠BAC=180°﹣(∠BAD+∠CAE)=90°.
∴AB⊥AC.
(2)AB⊥AC.理由如下:
同(1)一样可证得Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90°,即∠BAC=90°,
∴AB⊥AC.
23.
【答案】(1)证明见详解;(2)AF=DE+EF,理由见详解;(3)成立,理由见详解.
【详解】解:(1)证明:连接BF,如图,
∵△ABC≌△DBE(已知),
∴BC=BE,AC=DE.
∵∠ACB=∠DEB=90°,
∴∠BCF=∠BEF=90°.
在Rt△BFC和Rt△BFE中,
∴Rt△BFC≌Rt△BFE(HL).
∴CF=EF.
又∵AF+CF=AC,
∴AF+EF=DE.
(2)证明:连接BF,
∵△ABC≌△DBE,
∴BC=BE,
∵∠ACB=∠DEB=90°,
∴△BCF和△BEF是直角三角形,
在Rt△BCF和Rt△BEF中,
,
∴△BCF≌△BEF(HL),
∴CF=EF;
∵△ABC≌△DBE,
∴AC=DE,
∴AF=AC+FC=DE+EF.
(3)画出正确图形如图:
同(1)得CF=EF,
∵△ABC≌△DBE,
∴AC=DE,
∴AF+FC=AF+EF=AC=DE.
∴(1)中的结论AF+EF=DE仍然成立;
