2022-2023学年鲁教版(五四制)七年级数学上册 第一章三角形复习题 (含答案)
文档属性
| 名称 | 2022-2023学年鲁教版(五四制)七年级数学上册 第一章三角形复习题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 286.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-16 16:59:19 | ||
图片预览




文档简介
鲁教版七年级上册第一章三角形复习题
一、选择题(本大题共10小题,共40分)
图中,以为边的三角形有
A. 个
B. 个
C. 个
D. 个
已知的三个内角,,满足关系式,则此三角形
A. 一定有一个内角为 B. 一定有一个内角为
C. 一定是直角三角形 D. 一定是钝角三角形
如图,中,为的角平分线,为的高,与交于点,,,那么
A. B. C. D.
如图,在中,已知点,分别为边,上的中点,且,则的值为
A.
B.
C.
D.
如图,,,,垂足分别为,,,则下列说法不正确的是
A. 是的高
B. 是的高
C. 是的高
D. 是的高
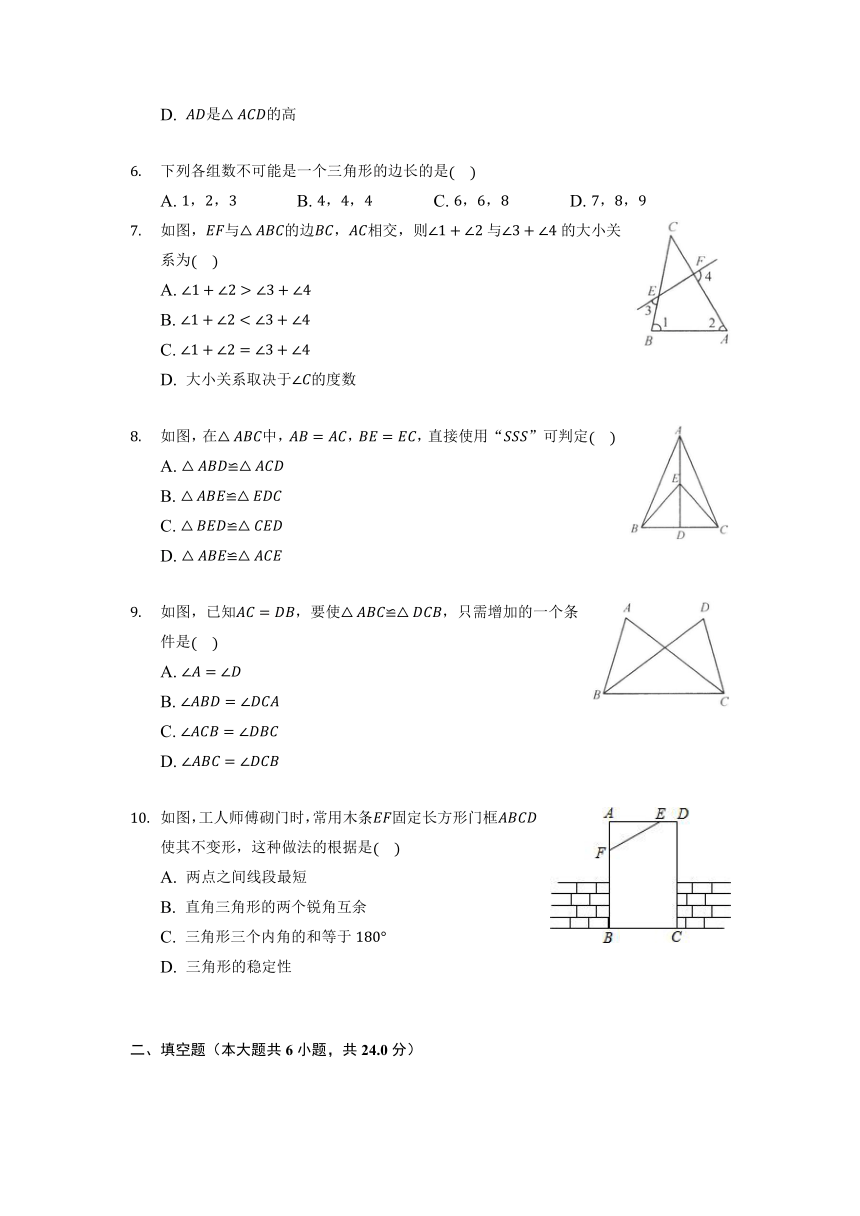
下列各组数不可能是一个三角形的边长的是
A. ,, B. ,, C. ,, D. ,,
如图,与的边,相交,则与的大小关系为
A.
B.
C.
D. 大小关系取决于的度数
如图,在中,,,直接使用“”可判定
A. ≌
B. ≌
C. ≌
D. ≌
如图,已知,要使≌,只需增加的一个条件是
A.
B.
C.
D.
如图,工人师傅砌门时,常用木条固定长方形门框,使其不变形,这种做法的根据是
A. 两点之间线段最短
B. 直角三角形的两个锐角互余
C. 三角形三个内角的和等于
D. 三角形的稳定性
二、填空题(本大题共6小题,共24.0分)
如图所示,在中,,平分,过点作于点,测得,,则的周长是 .
中,当时,这个三角形是 三角形.填“锐角”“直角”或“钝角”
一个等腰三角形的两边长分别为和,则这个等腰三角形的周长是 .
若≌,的周长为,且,,则的长为 .
如图,,且,,且,,,,计算图中实线所围成的图形的面积是 .
阅读下面材料:
数学课上,老师提出如下问题:
尺规作图:作一角等于已知角.
已知:图,
求作:,使得.
小明解答如图所示:
老师说:“小明作法正确.”小明的作图依据是: .
三、解答题(本大题共6小题,共56.0分)
如图,,,点在边上,,和相交于点试说明:≌.
如图,,直线分别交、于点、,点在上,点是直线上的一个动点点不与重合.
当点在射线上运动时,与有什么关系?说明理由;
当点在射线上运动时,与有什么关系?说明理由.
学校举办手工大赛,李明准备做一个“老鹰”风筝,李明用某种轻金属材料制成如图所示的一对翅膀的框架,已知,,,测得的周长为,,则制成这对翅膀的金属框架所需材料的总长度不少于多少?
如图,在中,,,于点.
试说明:;
若,,且的面积等于,求的长.
如图,在中,,角平分线,交于点.
求的度数;
点在上,,试说明:≌;
,,三条线段之间有怎样的数量关系?请直接写出结果.
已知:如图,在和中,,,.
求证:;;
如图,在和中,,,,则与的等量关系为________,的大小为________.
答案和解析
1.【答案】
【解析】解:题图中以为边的三角形有,,,,一共有个.
2.【答案】
【解析】略
3.【答案】
【解析】解:为的高,
.
,,
.
是的角平分线,
在中,,
, 故选A.
4.【答案】
【解析】略
5.【答案】
【解析】
【分析】
本题主要考查了三角形的高的知识,三角形的高是指从三角形的一个顶点向对边作垂线,连
接顶点与垂足之间的线段根据三角形高的定义选择正确的选项即可.
【解答】解:
A、不是的高,此选项符合题意
B、是的高,此选项不符合题意
C、是的高,此选项不符合题意
D、是的高,此选项不符合题意
故选A.
6.【答案】
【解析】略
7.【答案】
【解析】略
8.【答案】
【解析】略
9.【答案】
【解析】略
10.【答案】
【解析】略
11.【答案】
【解析】解:由,可得,
因为平分,所以,
又因为,所以≌,所以,
所以的周长为.
12.【答案】直角
【解析】解:在中,::::,,
设,
则,
解得,,
,,,
这个三角形是直角三角形,
故答案为:直角.
本题考查三角形内角和定理,解答本题的关键是明确题意,找出所求问题需要的条件,利用三角形内角和解答.根据三角形内角和定理和题目中三个内角的比值可以求得各个内角的度数,从而可以解答本题.
13.【答案】或
【解析】
【分析】
本题考查了等腰三角形的性质和三角形的三边关系.
由于未说明两边哪个是腰哪个是底,故需分:当等腰三角形的腰为当等腰三角形的腰为两种情况讨论,从而得到其周长.
【解答】
解:当等腰三角形的腰为,底为时,周长为;
当等腰三角形的腰为,底为时,周长为;
故这个等腰三角形的周长是或.
故答案为:或.
14.【答案】
【解析】略
15.【答案】
【解析】略
16.【答案】三边对应相等的两个三角形全等,全等三角形的对应角相等
【解析】略
17.【答案】解:因为,,,,
所以.
因为,
所以.
所以.
在和中,
所以≌.
【解析】略
18.【答案】解:
理由: ,
.
,
.
.
理由:如图, ,
.
,
.
【解析】见答案.
19.【答案】解,
,即,
在和中,
≌,
,
的周长为,,
制成这对翅膀的金属框架所需材料的总长度不少于.
【解析】见答案.
20.【答案】解:因为,,
所以.
在和中,
所以≌.
所以.
由,得≌,
所以.
因为,
所以.
又因为,,且的面积等于,
所以.
所以.
【解析】略
21.【答案】解:在中,,和分别平分和,
所以.
所以.
因为平分,
所以.
在和中,
所以≌.
所以.
因为,
所以.
所以.
在和中,
所以≌.
.
【解析】略
22.【答案】解:证明:,
,
在和中,
≌,
≌,
,
根据三角形内角和定理可知,
;.
【解析】见答案.
一、选择题(本大题共10小题,共40分)
图中,以为边的三角形有
A. 个
B. 个
C. 个
D. 个
已知的三个内角,,满足关系式,则此三角形
A. 一定有一个内角为 B. 一定有一个内角为
C. 一定是直角三角形 D. 一定是钝角三角形
如图,中,为的角平分线,为的高,与交于点,,,那么
A. B. C. D.
如图,在中,已知点,分别为边,上的中点,且,则的值为
A.
B.
C.
D.
如图,,,,垂足分别为,,,则下列说法不正确的是
A. 是的高
B. 是的高
C. 是的高
D. 是的高
下列各组数不可能是一个三角形的边长的是
A. ,, B. ,, C. ,, D. ,,
如图,与的边,相交,则与的大小关系为
A.
B.
C.
D. 大小关系取决于的度数
如图,在中,,,直接使用“”可判定
A. ≌
B. ≌
C. ≌
D. ≌
如图,已知,要使≌,只需增加的一个条件是
A.
B.
C.
D.
如图,工人师傅砌门时,常用木条固定长方形门框,使其不变形,这种做法的根据是
A. 两点之间线段最短
B. 直角三角形的两个锐角互余
C. 三角形三个内角的和等于
D. 三角形的稳定性
二、填空题(本大题共6小题,共24.0分)
如图所示,在中,,平分,过点作于点,测得,,则的周长是 .
中,当时,这个三角形是 三角形.填“锐角”“直角”或“钝角”
一个等腰三角形的两边长分别为和,则这个等腰三角形的周长是 .
若≌,的周长为,且,,则的长为 .
如图,,且,,且,,,,计算图中实线所围成的图形的面积是 .
阅读下面材料:
数学课上,老师提出如下问题:
尺规作图:作一角等于已知角.
已知:图,
求作:,使得.
小明解答如图所示:
老师说:“小明作法正确.”小明的作图依据是: .
三、解答题(本大题共6小题,共56.0分)
如图,,,点在边上,,和相交于点试说明:≌.
如图,,直线分别交、于点、,点在上,点是直线上的一个动点点不与重合.
当点在射线上运动时,与有什么关系?说明理由;
当点在射线上运动时,与有什么关系?说明理由.
学校举办手工大赛,李明准备做一个“老鹰”风筝,李明用某种轻金属材料制成如图所示的一对翅膀的框架,已知,,,测得的周长为,,则制成这对翅膀的金属框架所需材料的总长度不少于多少?
如图,在中,,,于点.
试说明:;
若,,且的面积等于,求的长.
如图,在中,,角平分线,交于点.
求的度数;
点在上,,试说明:≌;
,,三条线段之间有怎样的数量关系?请直接写出结果.
已知:如图,在和中,,,.
求证:;;
如图,在和中,,,,则与的等量关系为________,的大小为________.
答案和解析
1.【答案】
【解析】解:题图中以为边的三角形有,,,,一共有个.
2.【答案】
【解析】略
3.【答案】
【解析】解:为的高,
.
,,
.
是的角平分线,
在中,,
, 故选A.
4.【答案】
【解析】略
5.【答案】
【解析】
【分析】
本题主要考查了三角形的高的知识,三角形的高是指从三角形的一个顶点向对边作垂线,连
接顶点与垂足之间的线段根据三角形高的定义选择正确的选项即可.
【解答】解:
A、不是的高,此选项符合题意
B、是的高,此选项不符合题意
C、是的高,此选项不符合题意
D、是的高,此选项不符合题意
故选A.
6.【答案】
【解析】略
7.【答案】
【解析】略
8.【答案】
【解析】略
9.【答案】
【解析】略
10.【答案】
【解析】略
11.【答案】
【解析】解:由,可得,
因为平分,所以,
又因为,所以≌,所以,
所以的周长为.
12.【答案】直角
【解析】解:在中,::::,,
设,
则,
解得,,
,,,
这个三角形是直角三角形,
故答案为:直角.
本题考查三角形内角和定理,解答本题的关键是明确题意,找出所求问题需要的条件,利用三角形内角和解答.根据三角形内角和定理和题目中三个内角的比值可以求得各个内角的度数,从而可以解答本题.
13.【答案】或
【解析】
【分析】
本题考查了等腰三角形的性质和三角形的三边关系.
由于未说明两边哪个是腰哪个是底,故需分:当等腰三角形的腰为当等腰三角形的腰为两种情况讨论,从而得到其周长.
【解答】
解:当等腰三角形的腰为,底为时,周长为;
当等腰三角形的腰为,底为时,周长为;
故这个等腰三角形的周长是或.
故答案为:或.
14.【答案】
【解析】略
15.【答案】
【解析】略
16.【答案】三边对应相等的两个三角形全等,全等三角形的对应角相等
【解析】略
17.【答案】解:因为,,,,
所以.
因为,
所以.
所以.
在和中,
所以≌.
【解析】略
18.【答案】解:
理由: ,
.
,
.
.
理由:如图, ,
.
,
.
【解析】见答案.
19.【答案】解,
,即,
在和中,
≌,
,
的周长为,,
制成这对翅膀的金属框架所需材料的总长度不少于.
【解析】见答案.
20.【答案】解:因为,,
所以.
在和中,
所以≌.
所以.
由,得≌,
所以.
因为,
所以.
又因为,,且的面积等于,
所以.
所以.
【解析】略
21.【答案】解:在中,,和分别平分和,
所以.
所以.
因为平分,
所以.
在和中,
所以≌.
所以.
因为,
所以.
所以.
在和中,
所以≌.
.
【解析】略
22.【答案】解:证明:,
,
在和中,
≌,
≌,
,
根据三角形内角和定理可知,
;.
【解析】见答案.
