2022—2023学年人教版数学八年级上册 11.1.1 三角形的边 课件(共25张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册 11.1.1 三角形的边 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 814.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-16 17:02:48 | ||
图片预览







文档简介
(共25张PPT)
11.1.1 三角形的边
三角形
目标一 理解三角形相关的概念
定义 由 的三条线段 所
组成的图形叫做三角形.
不在同一条直线上
首尾顺次相接
例1 下面是小强用三根火柴组成的图形,其中符合三角形概念的是 ( )
图11-1-1
C
三角形概念的三注意
(1)三条线段;
(2)三个顶点不在同一条直线上;
(3)三条线段首尾顺次相接.
记 关键
例2 请你画一个三角形ABC,指出它的顶点、边、角分别是哪些,同时说明顶点、边的对应关系,并用符号表示三角形ABC.
解:如图,顶点分别为A,B,C;边分别为AB,BC,CA;
角分别为∠A,∠B,∠C;顶点A所对的边是BC;
顶点B所对的边是CA;顶点C所对的边是AB.
三角形ABC用符号表示为△ABC.
目标二 会把三角形分类
思考1 如何把三角形按最大角的度数进行分类,分成哪几类
解:当三角形的最大角分别是钝角、直角、锐角时,对应的三角
形分别为钝角三角形、直角三角形、锐角三角形.
思考2 三角形三条边中,按是否有边相等,可以将三角形分成哪两类 等腰三角形又可以分成哪两类 请用一个合适的形式表示此三角形分类.
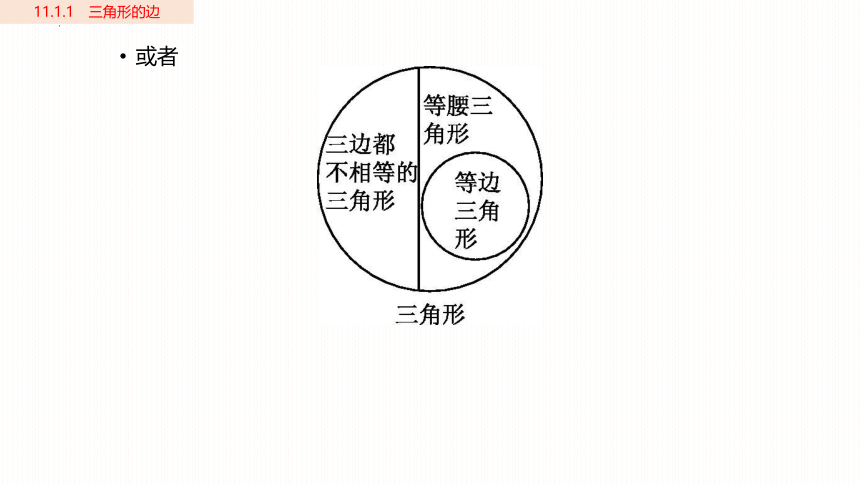
解:三角形按边的相等关系分类如下:
或者
目标三 三角形三边大小关系的推理及应用
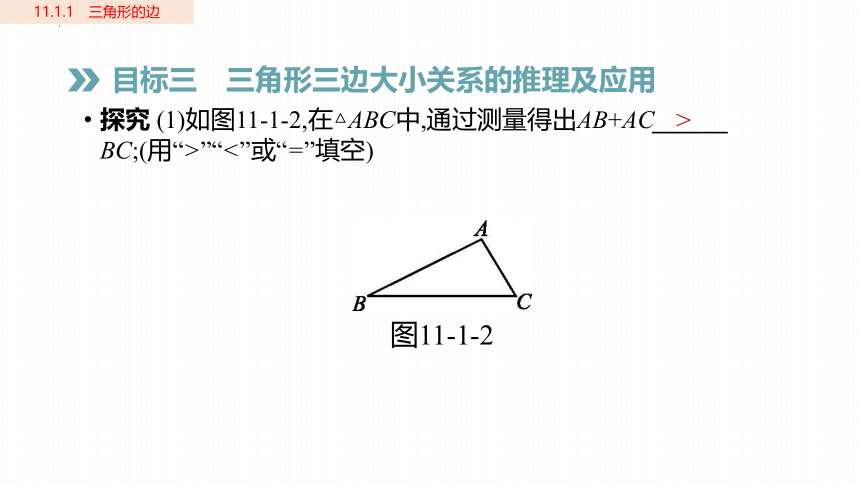
探究 (1)如图11-1-2,在△ABC中,通过测量得出AB+AC______ BC;(用“>”“<”或“=”填空)
图11-1-2
>
(2)对于△ABC,把B,C两顶点看成定点,由“两点之间,线段最短”得出AB+AC BC,同理:BC+AC AB,AB+BC
AC;(用“>”“<”或“=”填空)
(3)由BC+AC>AB移项可得,BC> .
图11-1-2
>
>
>
AB-AC
三角形的三边关系
三角形的任意一边,小于 ,大于 .
记 重点
其余两边之和
其余两边之差
例3 在△ABC中,AB=11,AC=2,并且BC的长为奇数,那么△ABC的周长为多少
解:根据三角形的三边关系,得11-2∵BC的长为奇数,
∴BC=11.
∴△ABC的周长为11+11+2=24.
变式 小王准备用一段长30 m的篱笆围成一个三角形形状的场地,用于饲养家兔,已知第一条边长为a m,由于受地势限制,第二条边长只能比第一条边长的2倍多2 m.
(1)请用含a的式子表示第三条边长;
解:由题意,得第二条边长为(2a+2)m,
∴第三条边长为30-a-(2a+2)=(28-3a)m.
(2)第一条边长可以为7 m吗 请说明理由.
解:第一条边长不可以为7 m.
理由:当a=7时,三条边长分别为7 m,16 m,7 m.
∵7+7<16,
∴不能构成三角形,即第一条边长不可以为7 m.
例4 (教材P3例题)用一条长为18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少
解:设底边长为x cm,则腰长为2x cm.
x+2x+2x=18.解得x=3.6.
所以,三边长分别为3.6 cm,7.2 cm,7.2 cm.
(2)能围成有一边的长是4 cm的等腰三角形吗 为什么
解:能.理由:因为长为4 cm的边可能是腰,也可能是底边,所以需要分情况讨论.
如果4 cm长的边为底边,设腰长为x cm,则4+2x=18.解得x=7.
如果4 cm长的边为腰,设底边长为x cm,则2×4+x=18.解得x=10.
因为4+4<10,不符合三角形两边的和大于第三边,
所以不能围成腰长是4 cm的等腰三角形.
由以上讨论可知,可以围成底边长是4 cm的等腰三角形.
根据等腰三角形边长的特点建立等量关系
腰长+腰长+底边长=等腰三角形的周长.
学 方法
变式 用一条长为20 cm的细绳围成一个等腰三角形,已知一边长是另一边长的2倍,则腰长为 .
8 cm
[解析] 设较短的边长为x cm,则较长的边长为2x cm.
①若较短的边为底边,较长的边为腰,则x+2x+2x=20,解得x=4.
此时三角形三边长分别为4 cm,8 cm,8 cm,能组成三角形;
②若较短的边为腰,较长的边为底边,则x+x+2x=20,解得x=5.
此时三角形三边长分别为5 cm,5 cm,10 cm.
∵5+5=10,
∴不满足三角形任意两边之和大于第三边,故不能组成三角形.
综上所述,等腰三角形的腰长为8 cm.
[小结]
1.三角形: 所
组成的图形叫做三角形.
2.三角形分类:三角形按三个内角的大小关系分为三类,分别
是 , , ;
三角形按边的相等关系分为两类,分别是________________
, .
由不在同一条直线上的三条线段首尾顺次相接
直角三角形
锐角三角形
钝角三角形
三边都不相等的
三角形
等腰三角形
3.如图11-1-3,由三角形三边大小关系可得,c-b图11-1-3
b+c
[检测]
1.如图11-1-4所示,以BC为边的三角形共有 ( )
A.1个 B.2个
C.3个 D.4个
图11-1-4
C
2.下列长度的三条线段能组成三角形的是 ( )
A.1,2,3 B.1,1,2
C.1,2,2 D.1,5,7
C
3.已知△ABC的三边长分别为4,9,x.
(1)求△ABC的周长的取值范围;
解:∵三角形的三边长分别为4,9,x,
∴9-4∴9+4+5<△ABC的周长<9+4+13,
即18<△ABC的周长<26.
(2)当△ABC的周长为偶数时,求x的值.
解:∵△ABC的周长是偶数,
∴由(1)的结果得△ABC的周长可以是20,22或24.
∴x的值为7,9或11.
11.1.1 三角形的边
三角形
目标一 理解三角形相关的概念
定义 由 的三条线段 所
组成的图形叫做三角形.
不在同一条直线上
首尾顺次相接
例1 下面是小强用三根火柴组成的图形,其中符合三角形概念的是 ( )
图11-1-1
C
三角形概念的三注意
(1)三条线段;
(2)三个顶点不在同一条直线上;
(3)三条线段首尾顺次相接.
记 关键
例2 请你画一个三角形ABC,指出它的顶点、边、角分别是哪些,同时说明顶点、边的对应关系,并用符号表示三角形ABC.
解:如图,顶点分别为A,B,C;边分别为AB,BC,CA;
角分别为∠A,∠B,∠C;顶点A所对的边是BC;
顶点B所对的边是CA;顶点C所对的边是AB.
三角形ABC用符号表示为△ABC.
目标二 会把三角形分类
思考1 如何把三角形按最大角的度数进行分类,分成哪几类
解:当三角形的最大角分别是钝角、直角、锐角时,对应的三角
形分别为钝角三角形、直角三角形、锐角三角形.
思考2 三角形三条边中,按是否有边相等,可以将三角形分成哪两类 等腰三角形又可以分成哪两类 请用一个合适的形式表示此三角形分类.
解:三角形按边的相等关系分类如下:
或者
目标三 三角形三边大小关系的推理及应用
探究 (1)如图11-1-2,在△ABC中,通过测量得出AB+AC______ BC;(用“>”“<”或“=”填空)
图11-1-2
>
(2)对于△ABC,把B,C两顶点看成定点,由“两点之间,线段最短”得出AB+AC BC,同理:BC+AC AB,AB+BC
AC;(用“>”“<”或“=”填空)
(3)由BC+AC>AB移项可得,BC> .
图11-1-2
>
>
>
AB-AC
三角形的三边关系
三角形的任意一边,小于 ,大于 .
记 重点
其余两边之和
其余两边之差
例3 在△ABC中,AB=11,AC=2,并且BC的长为奇数,那么△ABC的周长为多少
解:根据三角形的三边关系,得11-2
∴BC=11.
∴△ABC的周长为11+11+2=24.
变式 小王准备用一段长30 m的篱笆围成一个三角形形状的场地,用于饲养家兔,已知第一条边长为a m,由于受地势限制,第二条边长只能比第一条边长的2倍多2 m.
(1)请用含a的式子表示第三条边长;
解:由题意,得第二条边长为(2a+2)m,
∴第三条边长为30-a-(2a+2)=(28-3a)m.
(2)第一条边长可以为7 m吗 请说明理由.
解:第一条边长不可以为7 m.
理由:当a=7时,三条边长分别为7 m,16 m,7 m.
∵7+7<16,
∴不能构成三角形,即第一条边长不可以为7 m.
例4 (教材P3例题)用一条长为18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少
解:设底边长为x cm,则腰长为2x cm.
x+2x+2x=18.解得x=3.6.
所以,三边长分别为3.6 cm,7.2 cm,7.2 cm.
(2)能围成有一边的长是4 cm的等腰三角形吗 为什么
解:能.理由:因为长为4 cm的边可能是腰,也可能是底边,所以需要分情况讨论.
如果4 cm长的边为底边,设腰长为x cm,则4+2x=18.解得x=7.
如果4 cm长的边为腰,设底边长为x cm,则2×4+x=18.解得x=10.
因为4+4<10,不符合三角形两边的和大于第三边,
所以不能围成腰长是4 cm的等腰三角形.
由以上讨论可知,可以围成底边长是4 cm的等腰三角形.
根据等腰三角形边长的特点建立等量关系
腰长+腰长+底边长=等腰三角形的周长.
学 方法
变式 用一条长为20 cm的细绳围成一个等腰三角形,已知一边长是另一边长的2倍,则腰长为 .
8 cm
[解析] 设较短的边长为x cm,则较长的边长为2x cm.
①若较短的边为底边,较长的边为腰,则x+2x+2x=20,解得x=4.
此时三角形三边长分别为4 cm,8 cm,8 cm,能组成三角形;
②若较短的边为腰,较长的边为底边,则x+x+2x=20,解得x=5.
此时三角形三边长分别为5 cm,5 cm,10 cm.
∵5+5=10,
∴不满足三角形任意两边之和大于第三边,故不能组成三角形.
综上所述,等腰三角形的腰长为8 cm.
[小结]
1.三角形: 所
组成的图形叫做三角形.
2.三角形分类:三角形按三个内角的大小关系分为三类,分别
是 , , ;
三角形按边的相等关系分为两类,分别是________________
, .
由不在同一条直线上的三条线段首尾顺次相接
直角三角形
锐角三角形
钝角三角形
三边都不相等的
三角形
等腰三角形
3.如图11-1-3,由三角形三边大小关系可得,c-b
b+c
[检测]
1.如图11-1-4所示,以BC为边的三角形共有 ( )
A.1个 B.2个
C.3个 D.4个
图11-1-4
C
2.下列长度的三条线段能组成三角形的是 ( )
A.1,2,3 B.1,1,2
C.1,2,2 D.1,5,7
C
3.已知△ABC的三边长分别为4,9,x.
(1)求△ABC的周长的取值范围;
解:∵三角形的三边长分别为4,9,x,
∴9-4
即18<△ABC的周长<26.
(2)当△ABC的周长为偶数时,求x的值.
解:∵△ABC的周长是偶数,
∴由(1)的结果得△ABC的周长可以是20,22或24.
∴x的值为7,9或11.
