阶段练习1.1~2.3 全等三角形~设计轴对称图案-2022-2023学年苏科版数学八年级上册(含答案)
文档属性
| 名称 | 阶段练习1.1~2.3 全等三角形~设计轴对称图案-2022-2023学年苏科版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-16 22:01:43 | ||
图片预览


文档简介
阶段练习1.1~2.3:全等三角形~设计轴对称图案
-2022-2023学年苏科版数学八年级上册
一、选择题
1、(2022·海南省直辖县级单位·七年级期末)2022年冬奥会在北京举行,以下历届冬奥会会徽是轴对称图形的是( )
A. B. C. D.
2、(2022·湖北荆州·八年级期末)下列图形中对称轴的数量小于3的是( )
A. B. C. D.
3、(2022·湖南湘西·八年级期末)对于四个结论:①能够完全重合的两个图形叫全等图形;
②把沿直线BC翻折180°,得到,则;③三条边分别相等的两个三角形全等;④三个角分别相等的两个三角形全等.其中正确的结论有( )
A.②③④ B.①②④ C.①②③ D.①④
4、(2022·重庆开州·八年级期末)如图,已知,增加下列条件:①;②;③;④.其中不能保证的条件是( )
A.① B.② C.③ D.④
5、(2022·上海市徐汇中学七年级阶段练习)如图,小强拿一张正方形的纸,沿图甲中虚线对折一次得图乙,再对折一次得图丙,然后用剪刀沿图丙中的虚线剪去一个角,再打开后的形状是( )
A.B.C.D.
6、(2022·四川南充·一模)如图,每个小三角形都是等边三角形,再将1个小三角形涂黑,使4个小三角形构成轴对称图形.不同涂法有( )
A.2种 B.3种 C.4种 D.6种
7、(2021·江苏南京·八年级期中)如图,方格纸中△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,图中与△ABC全等的格点三角形的个数为(不含△ABC)( )
A.3 B.5 C.7 D.9
8、(2022·全国·八年级课时练习)如图,点P是外一点,点D,E分别是两边上的点,点P关于的对称点恰好落在线段上,点P关于的对称点落在的延长线上.若,则线段的长为( )
A.4 B.5 C.6 D.7
9、(2021泰州市第二中学附属初中八年级阶段练习)如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若∠AOB=40°,则∠MPN的度数是( )
A.90° B.100° C.120° D.140°
10、(2022·河北沧州·八年级期末)如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小,则∠AMN+∠ANM的度数为( )
A.130° B.120° C.110° D.100°
二、填空题
11、从汽车后视镜中看见某车牌后5位号码是,该号码实际是________.
12、(2022·河北保定·八年级期末)如图所示,△AOD关于直线l进行轴对称变换后得到△BOC,则以下结论中,不一定正确的是___________(填字母序号)
A. B. C.l垂直平分AB,且l垂直平分CD D.AC与BD互相平分
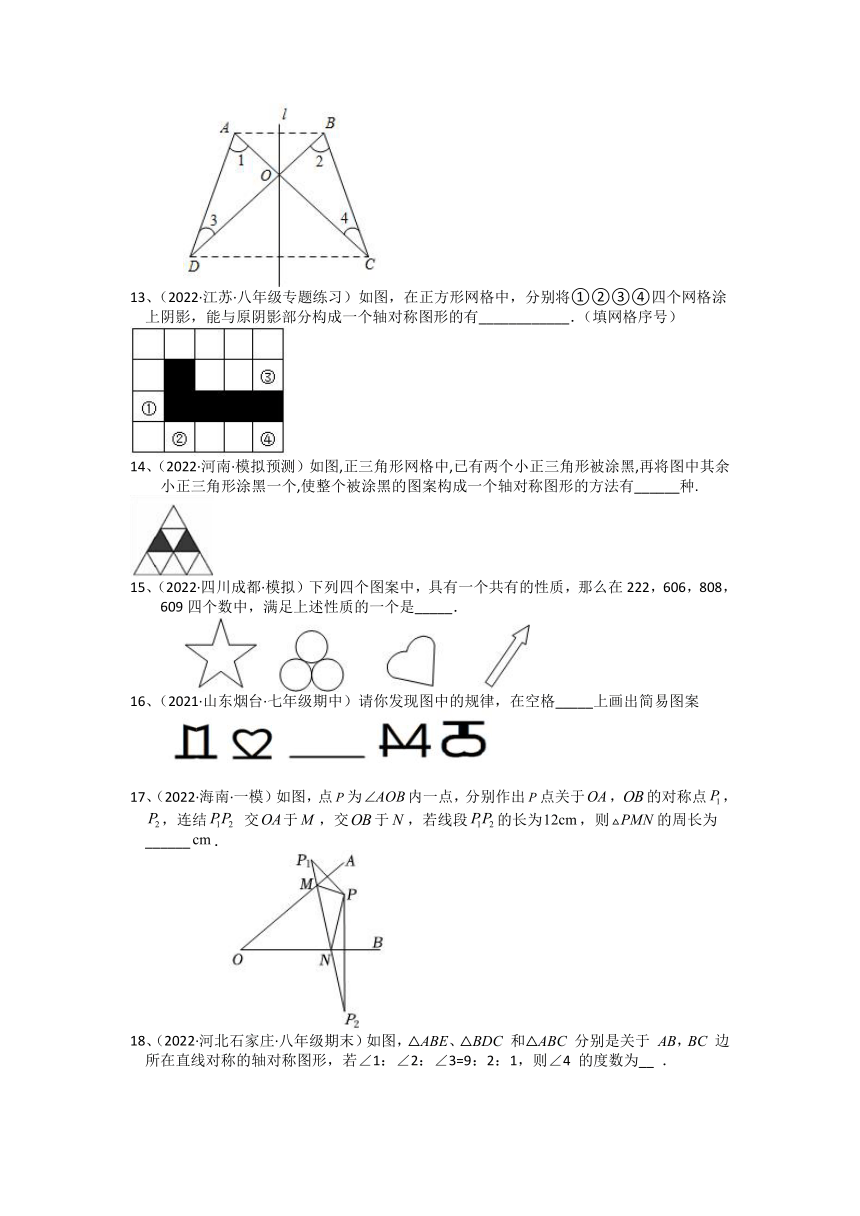
13、(2022·江苏·八年级专题练习)如图,在正方形网格中,分别将①②③④四个网格涂上阴影,能与原阴影部分构成一个轴对称图形的有____________.(填网格序号)
14、(2022·河南·模拟预测)如图,正三角形网格中,已有两个小正三角形被涂黑,再将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有______种.
15、(2022·四川成都·模拟)下列四个图案中,具有一个共有的性质,那么在222,606,808,609四个数中,满足上述性质的一个是_____.
16、(2021·山东烟台·七年级期中)请你发现图中的规律,在空格_____上画出简易图案
17、(2022·海南·一模)如图,点为内一点,分别作出点关于,的对称点,,连结 交于,交于,若线段的长为,则的周长为______.
18、(2022·河北石家庄·八年级期末)如图,△ABE、△BDC 和△ABC 分别是关于 AB,BC 边所在直线对称的轴对称图形,若∠1:∠2:∠3=9:2:1,则∠4 的度数为__ .
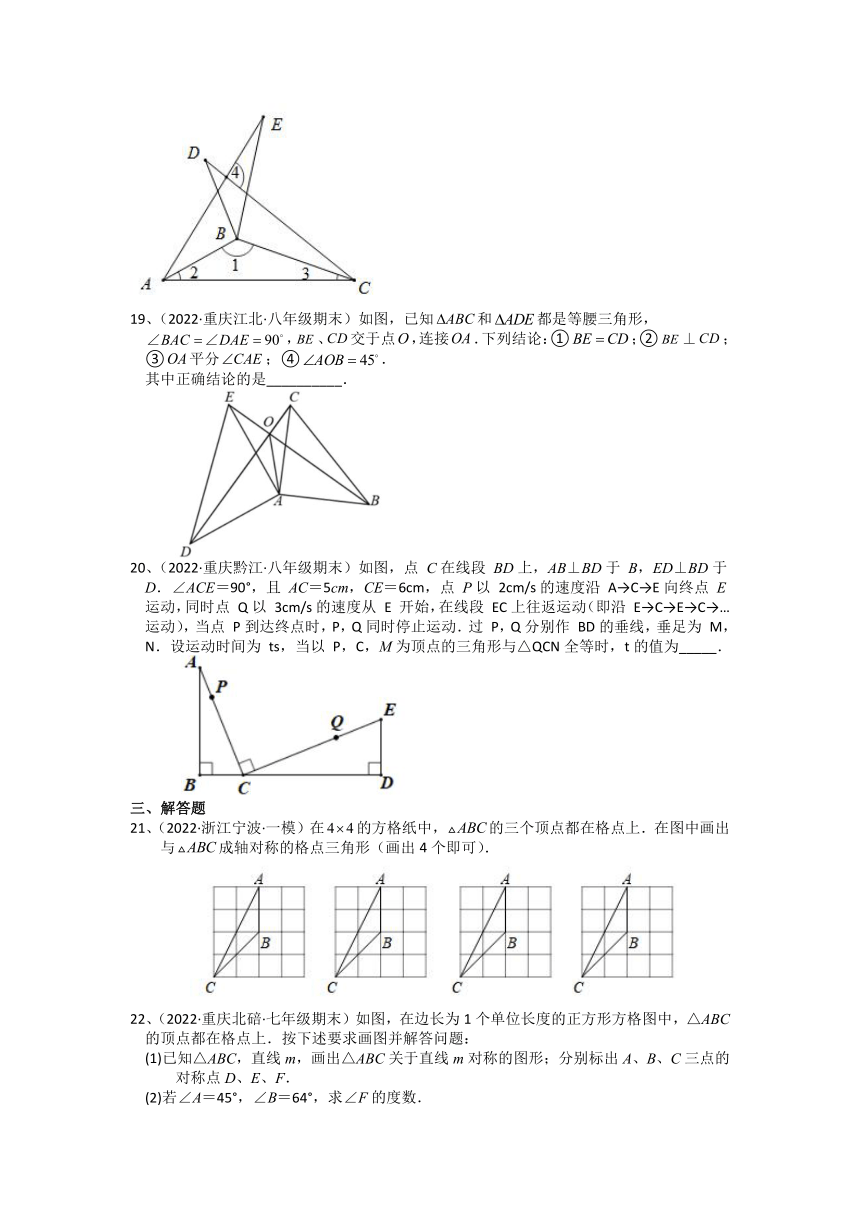
19、(2022·重庆江北·八年级期末)如图,已知和都是等腰三角形,,、交于点,连接.下列结论:①;②⊥;③平分;④.
其中正确结论的是__________.
20、(2022·重庆黔江·八年级期末)如图,点 C在线段 BD上,AB⊥BD于 B,ED⊥BD于 D.∠ACE=90°,且 AC=5cm,CE=6cm,点 P以 2cm/s的速度沿 A→C→E向终点 E运动,同时点 Q以 3cm/s的速度从 E 开始,在线段 EC上往返运动(即沿 E→C→E→C→…运动),当点 P到达终点时,P,Q同时停止运动.过 P,Q分别作 BD的垂线,垂足为 M,N.设运动时间为 ts,当以 P,C,M为顶点的三角形与△QCN全等时,t的值为_____.
三、解答题
21、(2022·浙江宁波·一模)在的方格纸中,的三个顶点都在格点上.在图中画出与成轴对称的格点三角形(画出4个即可).
22、(2022·重庆北碚·七年级期末)如图,在边长为1个单位长度的正方形方格图中,△ABC的顶点都在格点上.按下述要求画图并解答问题:
(1)已知△ABC,直线m,画出△ABC关于直线m对称的图形;分别标出A、B、C三点的对称点D、E、F.
(2)若∠A=45°,∠B=64°,求∠F的度数.
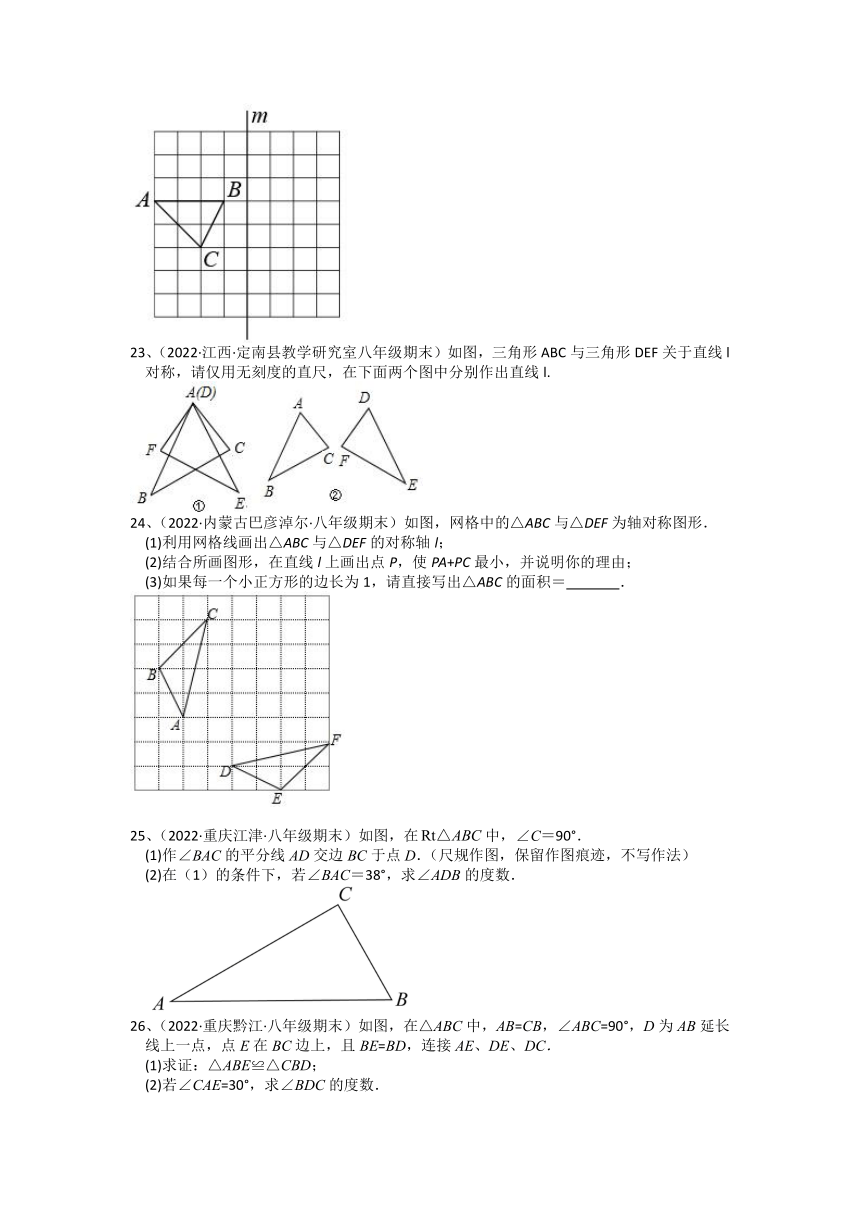
23、(2022·江西·定南县教学研究室八年级期末)如图,三角形ABC与三角形DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
24、(2022·内蒙古巴彦淖尔·八年级期末)如图,网格中的△ABC与△DEF为轴对称图形.
(1)利用网格线画出△ABC与△DEF的对称轴l;
(2)结合所画图形,在直线l上画出点P,使PA+PC最小,并说明你的理由;
(3)如果每一个小正方形的边长为1,请直接写出△ABC的面积= .
25、(2022·重庆江津·八年级期末)如图,在中,∠C=90°.
(1)作∠BAC的平分线AD交边BC于点D.(尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若∠BAC=38°,求∠ADB的度数.
26、(2022·重庆黔江·八年级期末)如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数.
27、(2022·重庆忠县·八年级期末)在中,点、分别在、边上,设与相交于点.
(1)如图①,设,、分别平分、,证明:.
(2)如图②,设,,点在的延长线上,连接、;若,,证明:.
28、(2022·河北廊坊·八年级期末)直角三角形ABC中,,直线l过点C.
(1)当时,如图1,分别过点A、B作于点D,于点E.,,
求DE长.
(2)当,时,如图2,点B与点F关于直线l对称,连接BF,CF,动点M从点A出发,以每秒1个单位长度的速度沿AC边向终点C运动,同时动点N从点F出发,以每秒3个单位的速度沿向终点F运动,点M、N到达相应的终点时停止运动,过点M作于点D,过点N作于点E,设运动时间为t秒.
①______,当N在路径上时,______.(用含t的代数式表示)
②直接写出当与全等时t的值.
29、(2022·内蒙古鄂尔多斯·八年级期末)【问题情境】利用角平分线构造全等三角形是常用的方法,如图1,OP平分.点A为OM上一点,过点A作,垂足为C,延长AC交ON于点B,可根据ASA证明,则,(即点C为AB的中点).
【问题探究】如图2,中,,,CD平分,,垂足E在CD的延长线上,试探究BE和CD的数量关系,并证明你的结论:
【拓展延伸】如图3,中,,,点D在线段BC上,且, 于E,DE交AB于F,试探究BE和DF之间的数量关系,并证明你的结论.
阶段练习1.1~2.3:全等三角形~设计轴对称图案
-2022-2023学年苏科版数学八年级上册
一、选择题
1、(2022·海南省直辖县级单位·七年级期末)2022年冬奥会在北京举行,以下历届冬奥会会徽是轴对称图形的是( )
A. B. C. D.
【答案】B
解:选项A、C、D不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
选项B能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
故选:B.
2、(2022·湖北荆州·八年级期末)下列图形中对称轴的数量小于3的是( )
A. B. C. D.
解:选项A一共有4条对称轴,故A不符合题意;
选项B一共有6条对称轴,故B不符合题意;
选项C一共有4条对称轴,故C不符合题意;
选项D一共有2条对称轴,故D符合题意.
故选:D.
3、(2022·湖南湘西·八年级期末)对于四个结论:①能够完全重合的两个图形叫全等图形;
②把沿直线BC翻折180°,得到,则;③三条边分别相等的两个三角形全等;④三个角分别相等的两个三角形全等.其中正确的结论有( )
A.②③④ B.①②④ C.①②③ D.①④
【详解】解:①能够完全重合的两个图形叫全等图形,正确;
②把△ABC沿直线BC翻折180°,得到△DBC,根据翻折性质得到∠A=∠D,正确;
③根据两个三角形全等的判定定理可知三条边分别相等的两个三角形全等,正确;
④根据两个三角形全等的判定定理,必须要有边,所以三个角分别相等的两个三角形不能判定它们相等全等,错误,其
中正确的结论有①②③,故选:C.
4、(2022·重庆开州·八年级期末)如图,已知,增加下列条件:①;②;③;④.其中不能保证的条件是( )
A.① B.② C.③ D.④
解:,,即,
,
当添加时,根据“”可判断;
当添加时,根据“”可判断;
当添加时,根据“”可判断;
当添加时,不能判断. 故选:D.
5、(2022·上海市徐汇中学七年级阶段练习)如图,小强拿一张正方形的纸,沿图甲中虚线对折一次得图乙,再对折一次得图丙,然后用剪刀沿图丙中的虚线剪去一个角,再打开后的形状是( )
A.B.C.D.
【答案】B
6、(2022·四川南充·一模)如图,每个小三角形都是等边三角形,再将1个小三角形涂黑,使4个小三角形构成轴对称图形.不同涂法有( )
A.2种 B.3种 C.4种 D.6种
【答案】C
【详解】解:如图所示,满足题意的涂色方式有4种,
故选:C.
7、(2021·江苏南京·八年级期中)如图,方格纸中△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,图中与△ABC全等的格点三角形的个数为(不含△ABC)( )
A.3 B.5 C.7 D.9
【答案】C
【详解】解:在图中画出格点三角形DEF,使得△DEF≌△ABC,
方法1,由正方形的轴对称性质画图,如以下4个图
由旋转性质,画以下3个图,
8、(2022·全国·八年级课时练习)如图,点P是外一点,点D,E分别是两边上的点,点P关于的对称点恰好落在线段上,点P关于的对称点落在的延长线上.若,则线段的长为( )
A.4 B.5 C.6 D.7
【答案】D
【详解】解:∵点P关于CA的对称点P1恰好落在线段ED上,P点关于CB的对称点P2落在ED的延长线上, ∴EP=EP,DP=DP,
∵PE=2,PD=4,DE=5,∴DP=4,EP=2, ∴DP=DE EP=5 2=3,
则线段PP的长为:PD+DP=4+3=7,故选:D.
9、(2021泰州市第二中学附属初中八年级阶段练习)如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若∠AOB=40°,则∠MPN的度数是( )
A.90° B.100° C.120° D.140°
【答案】B
解:∵与关于对称, ∴垂直平分, ∴平分, ∴
∵,∴, 同理可得,
∴
∴. 故选:B
10、(2022·河北沧州·八年级期末)如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小,则∠AMN+∠ANM的度数为( )
A.130° B.120° C.110° D.100°
【解析】根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,
如图,作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,
则A′A″即为△AMN的周长最小值.作DA延长线AH,
∵∠BAD=120°,∴∠HAA′=60°,∴∠AA′M+∠A″=∠HAA′=60°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°.
故选:B.
二、填空题
11、从汽车后视镜中看见某车牌后5位号码是,该号码实际是________.
解:关于镜面对称,也可以看成是关于某条直线对称,
∴关于某条直线对称的数字依次是BA629.故答案为:BA629.
12、(2022·河北保定·八年级期末)如图所示,△AOD关于直线l进行轴对称变换后得到△BOC,则以下结论中,不一定正确的是___________(填字母序号)
A. B. C.l垂直平分AB,且l垂直平分CD D.AC与BD互相平分
【答案】D
【详解】解:∵△AOD关于直线l进行轴对称变换后得到△BOC,
∴∠1=∠2,∠3=∠4,l垂直平分AB,且l垂直平分CD,故选项A、B、C正确;
∵四边形ABCD不一定是平行四边形,∴AC与BD不一定互相平分,故选项D不一定正确;
故答案为:D.
13、(2022·江苏·八年级专题练习)如图,在正方形网格中,分别将①②③④四个网格涂上阴影,能与原阴影部分构成一个轴对称图形的有____________.(填网格序号)
【答案】②③.
14、(2022·河南·模拟预测)如图,正三角形网格中,已有两个小正三角形被涂黑,再将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有______种.
【答案】3
【详解】解:选择小正三角形涂黑,使整个被涂黑的图案构成一个轴对称图形,
选择的位置有以下几种:1处,2处,3处,选择的位置共有3处.故答案为3.
15、(2022·四川成都·模拟)下列四个图案中,具有一个共有的性质,那么在222,606,808,609四个数中,满足上述性质的一个是_____.
【答案】808.
【详解】四个图案都是轴对称图形,在222,606,808,609四个数中,808是轴对称图形,
故答案为:808.
16、(2021·山东烟台·七年级期中)请你发现图中的规律,在空格_____上画出简易图案
【详解】解:为1的轴对称构成的图象,
为2的轴对称构成的图象,为4的轴对称构成的图象,
为5的轴对称构成的图象,
故横线上为3的轴对称构成的图象.故答案为.
17、(2022·海南·一模)如图,点为内一点,分别作出点关于,的对称点,,连结 交于,交于,若线段的长为,则的周长为______.
【答案】12
【详解】解:点关于、的对称点,,,,
的周长,故答案为:.
18、(2022·河北石家庄·八年级期末)如图,△ABE、△BDC 和△ABC 分别是关于 AB,BC 边所在直线对称的轴对称图形,若∠1:∠2:∠3=9:2:1,则∠4 的度数为__ .
解:由△ABE、△BDC 和△ABC 分别是关于 AB,BC 边所在直线对称的轴对称图形,可得:
∠EAB=∠2,∠3=∠DCB,
∠1:∠2:∠3=9:2:1,∠1+∠2+∠3=180°,,
; 故答案为90°.
19、(2022·重庆江北·八年级期末)如图,已知和都是等腰三角形,,、交于点,连接.下列结论:①;②⊥;③平分;④.
其中正确结论的是__________.
解:∵△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=90°,
∴AD=AE,AC=AB,∠DAC=∠DAE+ ∠EAC=∠BAC+ ∠EAC=∠EAB,
∴△DAC≌△EAB(SAS),∴CD=BE,∠ADC=∠AEB,故①正确:
∵∠ADE+∠AED=∠AED+∠EDO+∠ADC=180°-∠EAD=90°,
∴∠AED+∠EDO+∠AEB=90°,∴∠OED+∠ODE=90°,∴∠EOD=90°,∴BE⊥CD,故②正确:
如图,过点A分别作AM⊥CD与M,AN⊥BE于N,
∵△DAC≌△EAB,∴,∴AM=AN,∴OA平分∠BOD,
∵BE⊥CD,∴∠BOD=90°,∴∠AOD=∠AOB=45°,故④正确;
根据现有条件无法证明OA平分∠CAE,故③错误,
∴正确结论为①②④. 故答案为:①②④
20、(2022·重庆黔江·八年级期末)如图,点 C在线段 BD上,AB⊥BD于 B,ED⊥BD于 D.∠ACE=90°,且 AC=5cm,CE=6cm,点 P以 2cm/s的速度沿 A→C→E向终点 E运动,同时点 Q以 3cm/s的速度从 E 开始,在线段 EC上往返运动(即沿 E→C→E→C→…运动),当点 P到达终点时,P,Q同时停止运动.过 P,Q分别作 BD的垂线,垂足为 M,N.设运动时间为 ts,当以 P,C,M为顶点的三角形与△QCN全等时,t的值为_____.
解:当点P在AC上,点Q在CE上时,如图,
∵以P,C,M为顶点的三角形与△QCN全等,∴PC=CQ,
∴5﹣2t=6﹣3t,解得:t=1;
当点P在AC上,点Q第一次从点C返回时,
∵以P,C,M为顶点的三角形与△QCN全等,∴PC=CQ,
∴5﹣2t=3t﹣6,解得:t=;
当点P在CE上,点Q第一次从E点返回时,
∵以P,C,M为顶点的三角形与△QCN全等,
∴PC=CQ, ∴2t﹣5=18﹣3t,解得:t=;
综上所述:t的值为1或或. 故答案为:1或或.
三、解答题
21、(2022·浙江宁波·一模)在的方格纸中,的三个顶点都在格点上.在图中画出与成轴对称的格点三角形(画出4个即可).
【详解】解:如图所示,、、△、即为所求.
22、(2022·重庆北碚·七年级期末)如图,在边长为1个单位长度的正方形方格图中,△ABC的顶点都在格点上.按下述要求画图并解答问题:
(1)已知△ABC,直线m,画出△ABC关于直线m对称的图形;分别标出A、B、C三点的对称点D、E、F.
(2)若∠A=45°,∠B=64°,求∠F的度数.
解:(1)如图,△DEF即为所求;
(2)在△ABC中,∠A=45°,∠B=64°,∴∠C=180°-∠A-∠B=180°-45°-64°=71°,
∵△ABC与△DEF关于直线m对称,∴∠F=∠C=71°
23、(2022·江西·定南县教学研究室八年级期末)如图,三角形ABC与三角形DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
【解析】根据轴对称的性质,对应边所在直线的交点一定在对称轴上,
图①过点A和BC与EF的交点作直线即为对称轴直线l;
图②,延长两组对应边得到两个交点,然后过这两点作直线即为对称轴直线l.
图①中,过点A和BC,EF的交点作直线l;
图②中,过BC,EF延长线的交点和AC,DF延长线的交点作直线l.
24、(2022·内蒙古巴彦淖尔·八年级期末)如图,网格中的△ABC与△DEF为轴对称图形.
(1)利用网格线画出△ABC与△DEF的对称轴l;
(2)结合所画图形,在直线l上画出点P,使PA+PC最小,并说明你的理由;
(3)如果每一个小正方形的边长为1,请直接写出△ABC的面积= .
解:(1)解:如图所示,直线l即为所求.
(2)解:如图所示,点P即为所求;根据两点之间线段最短即可证明PA+PC最小;
(3)解:△ABC的面积=2×4﹣×1×2﹣×1×4﹣×2×2=3,故答案为:3.
25、(2022·重庆江津·八年级期末)如图,在中,∠C=90°.
(1)作∠BAC的平分线AD交边BC于点D.(尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若∠BAC=38°,求∠ADB的度数.
解:(1)如图,AD即为所作:
(2)∵AD平分∠BAC,∠BAC=38°,∴,
∵∠C=90°,∴∠ADB=∠CAD+∠C=109°.
26、(2022·重庆黔江·八年级期末)如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数.
解:(1)证明:∵∠ABC=90°,∴∠DBC=90°,
在△ABE和△CBD中,∴△ABE≌△CBD(SAS);
(2)∵AB=CB,∠ABC=90°,∴∠BCA=45°,∴∠AEB=∠CAE+∠BCA=30°+45°=75°,
∵△ABE≌△CBD,∴∠BDC=∠AEB=75°.
27、(2022·重庆忠县·八年级期末)在中,点、分别在、边上,设与相交于点.
(1)如图①,设,、分别平分、,证明:.
(2)如图②,设,,点在的延长线上,连接、;若,,证明:.
解:(1)在上截取,连接,
在中, ;,
∵、分别平分、,∴
∴
∵ ∴
,
在和中,,,,
,,,
,,
平分,,
又,,,;
(2),,,
,,且,,
又,,,
而,,
而,即,,.
28、(2022·河北廊坊·八年级期末)直角三角形ABC中,,直线l过点C.
(1)当时,如图1,分别过点A、B作于点D,于点E.,,
求DE长.
(2)当,时,如图2,点B与点F关于直线l对称,连接BF,CF,动点M从点A出发,以每秒1个单位长度的速度沿AC边向终点C运动,同时动点N从点F出发,以每秒3个单位的速度沿向终点F运动,点M、N到达相应的终点时停止运动,过点M作于点D,过点N作于点E,设运动时间为t秒.
①______,当N在路径上时,______.(用含t的代数式表示)
②直接写出当与全等时t的值.
【答案】(1);(2)①;②当t=秒或5秒或秒时,△MDC与△CEN全等.
解:(1)∵AD⊥直线l, ∴∠DAC+∠ACD=90°,
∵∠ACB=90°, ∴∠BCE+∠ACD=90°, ∴∠DAC=∠ECB,
,;
, ∴△ACD≌△CBE(AAS);而,,
(2)①由题意得,AM=t,
,, 点B与点F关于直线l对称,
当N在路径上时, 故答案为:
②由轴对称的性质可知,∠BCE=∠FCE,
∵,; ,∠MCD+∠CMD=90°,∠MCD+∠BCE=90°,
∴∠NCE=∠CMD,
∴当CM=CN时,△MDC与△CEN全等,
当点N 沿F→C路径运动时,8-t=6-3t, 解得,t=-1(不合题意),
当点N 沿C→B路径运动时,此时 ; 8-t=3t-6, 解得,,
当点N 沿B→C路径运动时,此时;由题意得,8-t=18-3t, 解得,t=5,
当点N 沿C→F路径运动时,此时 ;由题意得,8-t=3t-18, 解得,,
综上所述,当t=秒或5秒或秒时,△MDC与△CEN全等.
29、(2022·内蒙古鄂尔多斯·八年级期末)【问题情境】利用角平分线构造全等三角形是常用的方法,如图1,OP平分.点A为OM上一点,过点A作,垂足为C,延长AC交ON于点B,可根据ASA证明,则,(即点C为AB的中点).
【问题探究】如图2,中,,,CD平分,,垂足E在CD的延长线上,试探究BE和CD的数量关系,并证明你的结论:
【拓展延伸】如图3,中,,,点D在线段BC上,且, 于E,DE交AB于F,试探究BE和DF之间的数量关系,并证明你的结论.
【问题探究】,证明见解析;【拓展延伸】.证明见解析【问题探究】延长BE交CA延长线于F,证明,推出,再证明,可得结论;
【拓展延伸】过点D作,交BE的延长线于点G,与AE相交于H,证明,推出,再证明得到来求解.
解:问题探究:,理由如下:
延长BE交CA延长线于F,∵CD平分,∴,
在和中,,∴,∴.,
∵,∴,∴,
在和中,,∴,∴,∴;
拓展延伸:.
证明:过点D作,交BE的延长线于点G,与AE相交于H,
∵,∴,,
∵,∴.
∵,∴,∴,
∵,∴.
∵,,∴.
∵,∴,∴,∴,
在和中,,∴;∴,
在和中,,∴
∴, ∴.
-2022-2023学年苏科版数学八年级上册
一、选择题
1、(2022·海南省直辖县级单位·七年级期末)2022年冬奥会在北京举行,以下历届冬奥会会徽是轴对称图形的是( )
A. B. C. D.
2、(2022·湖北荆州·八年级期末)下列图形中对称轴的数量小于3的是( )
A. B. C. D.
3、(2022·湖南湘西·八年级期末)对于四个结论:①能够完全重合的两个图形叫全等图形;
②把沿直线BC翻折180°,得到,则;③三条边分别相等的两个三角形全等;④三个角分别相等的两个三角形全等.其中正确的结论有( )
A.②③④ B.①②④ C.①②③ D.①④
4、(2022·重庆开州·八年级期末)如图,已知,增加下列条件:①;②;③;④.其中不能保证的条件是( )
A.① B.② C.③ D.④
5、(2022·上海市徐汇中学七年级阶段练习)如图,小强拿一张正方形的纸,沿图甲中虚线对折一次得图乙,再对折一次得图丙,然后用剪刀沿图丙中的虚线剪去一个角,再打开后的形状是( )
A.B.C.D.
6、(2022·四川南充·一模)如图,每个小三角形都是等边三角形,再将1个小三角形涂黑,使4个小三角形构成轴对称图形.不同涂法有( )
A.2种 B.3种 C.4种 D.6种
7、(2021·江苏南京·八年级期中)如图,方格纸中△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,图中与△ABC全等的格点三角形的个数为(不含△ABC)( )
A.3 B.5 C.7 D.9
8、(2022·全国·八年级课时练习)如图,点P是外一点,点D,E分别是两边上的点,点P关于的对称点恰好落在线段上,点P关于的对称点落在的延长线上.若,则线段的长为( )
A.4 B.5 C.6 D.7
9、(2021泰州市第二中学附属初中八年级阶段练习)如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若∠AOB=40°,则∠MPN的度数是( )
A.90° B.100° C.120° D.140°
10、(2022·河北沧州·八年级期末)如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小,则∠AMN+∠ANM的度数为( )
A.130° B.120° C.110° D.100°
二、填空题
11、从汽车后视镜中看见某车牌后5位号码是,该号码实际是________.
12、(2022·河北保定·八年级期末)如图所示,△AOD关于直线l进行轴对称变换后得到△BOC,则以下结论中,不一定正确的是___________(填字母序号)
A. B. C.l垂直平分AB,且l垂直平分CD D.AC与BD互相平分
13、(2022·江苏·八年级专题练习)如图,在正方形网格中,分别将①②③④四个网格涂上阴影,能与原阴影部分构成一个轴对称图形的有____________.(填网格序号)
14、(2022·河南·模拟预测)如图,正三角形网格中,已有两个小正三角形被涂黑,再将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有______种.
15、(2022·四川成都·模拟)下列四个图案中,具有一个共有的性质,那么在222,606,808,609四个数中,满足上述性质的一个是_____.
16、(2021·山东烟台·七年级期中)请你发现图中的规律,在空格_____上画出简易图案
17、(2022·海南·一模)如图,点为内一点,分别作出点关于,的对称点,,连结 交于,交于,若线段的长为,则的周长为______.
18、(2022·河北石家庄·八年级期末)如图,△ABE、△BDC 和△ABC 分别是关于 AB,BC 边所在直线对称的轴对称图形,若∠1:∠2:∠3=9:2:1,则∠4 的度数为__ .
19、(2022·重庆江北·八年级期末)如图,已知和都是等腰三角形,,、交于点,连接.下列结论:①;②⊥;③平分;④.
其中正确结论的是__________.
20、(2022·重庆黔江·八年级期末)如图,点 C在线段 BD上,AB⊥BD于 B,ED⊥BD于 D.∠ACE=90°,且 AC=5cm,CE=6cm,点 P以 2cm/s的速度沿 A→C→E向终点 E运动,同时点 Q以 3cm/s的速度从 E 开始,在线段 EC上往返运动(即沿 E→C→E→C→…运动),当点 P到达终点时,P,Q同时停止运动.过 P,Q分别作 BD的垂线,垂足为 M,N.设运动时间为 ts,当以 P,C,M为顶点的三角形与△QCN全等时,t的值为_____.
三、解答题
21、(2022·浙江宁波·一模)在的方格纸中,的三个顶点都在格点上.在图中画出与成轴对称的格点三角形(画出4个即可).
22、(2022·重庆北碚·七年级期末)如图,在边长为1个单位长度的正方形方格图中,△ABC的顶点都在格点上.按下述要求画图并解答问题:
(1)已知△ABC,直线m,画出△ABC关于直线m对称的图形;分别标出A、B、C三点的对称点D、E、F.
(2)若∠A=45°,∠B=64°,求∠F的度数.
23、(2022·江西·定南县教学研究室八年级期末)如图,三角形ABC与三角形DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
24、(2022·内蒙古巴彦淖尔·八年级期末)如图,网格中的△ABC与△DEF为轴对称图形.
(1)利用网格线画出△ABC与△DEF的对称轴l;
(2)结合所画图形,在直线l上画出点P,使PA+PC最小,并说明你的理由;
(3)如果每一个小正方形的边长为1,请直接写出△ABC的面积= .
25、(2022·重庆江津·八年级期末)如图,在中,∠C=90°.
(1)作∠BAC的平分线AD交边BC于点D.(尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若∠BAC=38°,求∠ADB的度数.
26、(2022·重庆黔江·八年级期末)如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数.
27、(2022·重庆忠县·八年级期末)在中,点、分别在、边上,设与相交于点.
(1)如图①,设,、分别平分、,证明:.
(2)如图②,设,,点在的延长线上,连接、;若,,证明:.
28、(2022·河北廊坊·八年级期末)直角三角形ABC中,,直线l过点C.
(1)当时,如图1,分别过点A、B作于点D,于点E.,,
求DE长.
(2)当,时,如图2,点B与点F关于直线l对称,连接BF,CF,动点M从点A出发,以每秒1个单位长度的速度沿AC边向终点C运动,同时动点N从点F出发,以每秒3个单位的速度沿向终点F运动,点M、N到达相应的终点时停止运动,过点M作于点D,过点N作于点E,设运动时间为t秒.
①______,当N在路径上时,______.(用含t的代数式表示)
②直接写出当与全等时t的值.
29、(2022·内蒙古鄂尔多斯·八年级期末)【问题情境】利用角平分线构造全等三角形是常用的方法,如图1,OP平分.点A为OM上一点,过点A作,垂足为C,延长AC交ON于点B,可根据ASA证明,则,(即点C为AB的中点).
【问题探究】如图2,中,,,CD平分,,垂足E在CD的延长线上,试探究BE和CD的数量关系,并证明你的结论:
【拓展延伸】如图3,中,,,点D在线段BC上,且, 于E,DE交AB于F,试探究BE和DF之间的数量关系,并证明你的结论.
阶段练习1.1~2.3:全等三角形~设计轴对称图案
-2022-2023学年苏科版数学八年级上册
一、选择题
1、(2022·海南省直辖县级单位·七年级期末)2022年冬奥会在北京举行,以下历届冬奥会会徽是轴对称图形的是( )
A. B. C. D.
【答案】B
解:选项A、C、D不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
选项B能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
故选:B.
2、(2022·湖北荆州·八年级期末)下列图形中对称轴的数量小于3的是( )
A. B. C. D.
解:选项A一共有4条对称轴,故A不符合题意;
选项B一共有6条对称轴,故B不符合题意;
选项C一共有4条对称轴,故C不符合题意;
选项D一共有2条对称轴,故D符合题意.
故选:D.
3、(2022·湖南湘西·八年级期末)对于四个结论:①能够完全重合的两个图形叫全等图形;
②把沿直线BC翻折180°,得到,则;③三条边分别相等的两个三角形全等;④三个角分别相等的两个三角形全等.其中正确的结论有( )
A.②③④ B.①②④ C.①②③ D.①④
【详解】解:①能够完全重合的两个图形叫全等图形,正确;
②把△ABC沿直线BC翻折180°,得到△DBC,根据翻折性质得到∠A=∠D,正确;
③根据两个三角形全等的判定定理可知三条边分别相等的两个三角形全等,正确;
④根据两个三角形全等的判定定理,必须要有边,所以三个角分别相等的两个三角形不能判定它们相等全等,错误,其
中正确的结论有①②③,故选:C.
4、(2022·重庆开州·八年级期末)如图,已知,增加下列条件:①;②;③;④.其中不能保证的条件是( )
A.① B.② C.③ D.④
解:,,即,
,
当添加时,根据“”可判断;
当添加时,根据“”可判断;
当添加时,根据“”可判断;
当添加时,不能判断. 故选:D.
5、(2022·上海市徐汇中学七年级阶段练习)如图,小强拿一张正方形的纸,沿图甲中虚线对折一次得图乙,再对折一次得图丙,然后用剪刀沿图丙中的虚线剪去一个角,再打开后的形状是( )
A.B.C.D.
【答案】B
6、(2022·四川南充·一模)如图,每个小三角形都是等边三角形,再将1个小三角形涂黑,使4个小三角形构成轴对称图形.不同涂法有( )
A.2种 B.3种 C.4种 D.6种
【答案】C
【详解】解:如图所示,满足题意的涂色方式有4种,
故选:C.
7、(2021·江苏南京·八年级期中)如图,方格纸中△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,图中与△ABC全等的格点三角形的个数为(不含△ABC)( )
A.3 B.5 C.7 D.9
【答案】C
【详解】解:在图中画出格点三角形DEF,使得△DEF≌△ABC,
方法1,由正方形的轴对称性质画图,如以下4个图
由旋转性质,画以下3个图,
8、(2022·全国·八年级课时练习)如图,点P是外一点,点D,E分别是两边上的点,点P关于的对称点恰好落在线段上,点P关于的对称点落在的延长线上.若,则线段的长为( )
A.4 B.5 C.6 D.7
【答案】D
【详解】解:∵点P关于CA的对称点P1恰好落在线段ED上,P点关于CB的对称点P2落在ED的延长线上, ∴EP=EP,DP=DP,
∵PE=2,PD=4,DE=5,∴DP=4,EP=2, ∴DP=DE EP=5 2=3,
则线段PP的长为:PD+DP=4+3=7,故选:D.
9、(2021泰州市第二中学附属初中八年级阶段练习)如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若∠AOB=40°,则∠MPN的度数是( )
A.90° B.100° C.120° D.140°
【答案】B
解:∵与关于对称, ∴垂直平分, ∴平分, ∴
∵,∴, 同理可得,
∴
∴. 故选:B
10、(2022·河北沧州·八年级期末)如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小,则∠AMN+∠ANM的度数为( )
A.130° B.120° C.110° D.100°
【解析】根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,
如图,作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,
则A′A″即为△AMN的周长最小值.作DA延长线AH,
∵∠BAD=120°,∴∠HAA′=60°,∴∠AA′M+∠A″=∠HAA′=60°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°.
故选:B.
二、填空题
11、从汽车后视镜中看见某车牌后5位号码是,该号码实际是________.
解:关于镜面对称,也可以看成是关于某条直线对称,
∴关于某条直线对称的数字依次是BA629.故答案为:BA629.
12、(2022·河北保定·八年级期末)如图所示,△AOD关于直线l进行轴对称变换后得到△BOC,则以下结论中,不一定正确的是___________(填字母序号)
A. B. C.l垂直平分AB,且l垂直平分CD D.AC与BD互相平分
【答案】D
【详解】解:∵△AOD关于直线l进行轴对称变换后得到△BOC,
∴∠1=∠2,∠3=∠4,l垂直平分AB,且l垂直平分CD,故选项A、B、C正确;
∵四边形ABCD不一定是平行四边形,∴AC与BD不一定互相平分,故选项D不一定正确;
故答案为:D.
13、(2022·江苏·八年级专题练习)如图,在正方形网格中,分别将①②③④四个网格涂上阴影,能与原阴影部分构成一个轴对称图形的有____________.(填网格序号)
【答案】②③.
14、(2022·河南·模拟预测)如图,正三角形网格中,已有两个小正三角形被涂黑,再将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有______种.
【答案】3
【详解】解:选择小正三角形涂黑,使整个被涂黑的图案构成一个轴对称图形,
选择的位置有以下几种:1处,2处,3处,选择的位置共有3处.故答案为3.
15、(2022·四川成都·模拟)下列四个图案中,具有一个共有的性质,那么在222,606,808,609四个数中,满足上述性质的一个是_____.
【答案】808.
【详解】四个图案都是轴对称图形,在222,606,808,609四个数中,808是轴对称图形,
故答案为:808.
16、(2021·山东烟台·七年级期中)请你发现图中的规律,在空格_____上画出简易图案
【详解】解:为1的轴对称构成的图象,
为2的轴对称构成的图象,为4的轴对称构成的图象,
为5的轴对称构成的图象,
故横线上为3的轴对称构成的图象.故答案为.
17、(2022·海南·一模)如图,点为内一点,分别作出点关于,的对称点,,连结 交于,交于,若线段的长为,则的周长为______.
【答案】12
【详解】解:点关于、的对称点,,,,
的周长,故答案为:.
18、(2022·河北石家庄·八年级期末)如图,△ABE、△BDC 和△ABC 分别是关于 AB,BC 边所在直线对称的轴对称图形,若∠1:∠2:∠3=9:2:1,则∠4 的度数为__ .
解:由△ABE、△BDC 和△ABC 分别是关于 AB,BC 边所在直线对称的轴对称图形,可得:
∠EAB=∠2,∠3=∠DCB,
∠1:∠2:∠3=9:2:1,∠1+∠2+∠3=180°,,
; 故答案为90°.
19、(2022·重庆江北·八年级期末)如图,已知和都是等腰三角形,,、交于点,连接.下列结论:①;②⊥;③平分;④.
其中正确结论的是__________.
解:∵△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=90°,
∴AD=AE,AC=AB,∠DAC=∠DAE+ ∠EAC=∠BAC+ ∠EAC=∠EAB,
∴△DAC≌△EAB(SAS),∴CD=BE,∠ADC=∠AEB,故①正确:
∵∠ADE+∠AED=∠AED+∠EDO+∠ADC=180°-∠EAD=90°,
∴∠AED+∠EDO+∠AEB=90°,∴∠OED+∠ODE=90°,∴∠EOD=90°,∴BE⊥CD,故②正确:
如图,过点A分别作AM⊥CD与M,AN⊥BE于N,
∵△DAC≌△EAB,∴,∴AM=AN,∴OA平分∠BOD,
∵BE⊥CD,∴∠BOD=90°,∴∠AOD=∠AOB=45°,故④正确;
根据现有条件无法证明OA平分∠CAE,故③错误,
∴正确结论为①②④. 故答案为:①②④
20、(2022·重庆黔江·八年级期末)如图,点 C在线段 BD上,AB⊥BD于 B,ED⊥BD于 D.∠ACE=90°,且 AC=5cm,CE=6cm,点 P以 2cm/s的速度沿 A→C→E向终点 E运动,同时点 Q以 3cm/s的速度从 E 开始,在线段 EC上往返运动(即沿 E→C→E→C→…运动),当点 P到达终点时,P,Q同时停止运动.过 P,Q分别作 BD的垂线,垂足为 M,N.设运动时间为 ts,当以 P,C,M为顶点的三角形与△QCN全等时,t的值为_____.
解:当点P在AC上,点Q在CE上时,如图,
∵以P,C,M为顶点的三角形与△QCN全等,∴PC=CQ,
∴5﹣2t=6﹣3t,解得:t=1;
当点P在AC上,点Q第一次从点C返回时,
∵以P,C,M为顶点的三角形与△QCN全等,∴PC=CQ,
∴5﹣2t=3t﹣6,解得:t=;
当点P在CE上,点Q第一次从E点返回时,
∵以P,C,M为顶点的三角形与△QCN全等,
∴PC=CQ, ∴2t﹣5=18﹣3t,解得:t=;
综上所述:t的值为1或或. 故答案为:1或或.
三、解答题
21、(2022·浙江宁波·一模)在的方格纸中,的三个顶点都在格点上.在图中画出与成轴对称的格点三角形(画出4个即可).
【详解】解:如图所示,、、△、即为所求.
22、(2022·重庆北碚·七年级期末)如图,在边长为1个单位长度的正方形方格图中,△ABC的顶点都在格点上.按下述要求画图并解答问题:
(1)已知△ABC,直线m,画出△ABC关于直线m对称的图形;分别标出A、B、C三点的对称点D、E、F.
(2)若∠A=45°,∠B=64°,求∠F的度数.
解:(1)如图,△DEF即为所求;
(2)在△ABC中,∠A=45°,∠B=64°,∴∠C=180°-∠A-∠B=180°-45°-64°=71°,
∵△ABC与△DEF关于直线m对称,∴∠F=∠C=71°
23、(2022·江西·定南县教学研究室八年级期末)如图,三角形ABC与三角形DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
【解析】根据轴对称的性质,对应边所在直线的交点一定在对称轴上,
图①过点A和BC与EF的交点作直线即为对称轴直线l;
图②,延长两组对应边得到两个交点,然后过这两点作直线即为对称轴直线l.
图①中,过点A和BC,EF的交点作直线l;
图②中,过BC,EF延长线的交点和AC,DF延长线的交点作直线l.
24、(2022·内蒙古巴彦淖尔·八年级期末)如图,网格中的△ABC与△DEF为轴对称图形.
(1)利用网格线画出△ABC与△DEF的对称轴l;
(2)结合所画图形,在直线l上画出点P,使PA+PC最小,并说明你的理由;
(3)如果每一个小正方形的边长为1,请直接写出△ABC的面积= .
解:(1)解:如图所示,直线l即为所求.
(2)解:如图所示,点P即为所求;根据两点之间线段最短即可证明PA+PC最小;
(3)解:△ABC的面积=2×4﹣×1×2﹣×1×4﹣×2×2=3,故答案为:3.
25、(2022·重庆江津·八年级期末)如图,在中,∠C=90°.
(1)作∠BAC的平分线AD交边BC于点D.(尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若∠BAC=38°,求∠ADB的度数.
解:(1)如图,AD即为所作:
(2)∵AD平分∠BAC,∠BAC=38°,∴,
∵∠C=90°,∴∠ADB=∠CAD+∠C=109°.
26、(2022·重庆黔江·八年级期末)如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数.
解:(1)证明:∵∠ABC=90°,∴∠DBC=90°,
在△ABE和△CBD中,∴△ABE≌△CBD(SAS);
(2)∵AB=CB,∠ABC=90°,∴∠BCA=45°,∴∠AEB=∠CAE+∠BCA=30°+45°=75°,
∵△ABE≌△CBD,∴∠BDC=∠AEB=75°.
27、(2022·重庆忠县·八年级期末)在中,点、分别在、边上,设与相交于点.
(1)如图①,设,、分别平分、,证明:.
(2)如图②,设,,点在的延长线上,连接、;若,,证明:.
解:(1)在上截取,连接,
在中, ;,
∵、分别平分、,∴
∴
∵ ∴
,
在和中,,,,
,,,
,,
平分,,
又,,,;
(2),,,
,,且,,
又,,,
而,,
而,即,,.
28、(2022·河北廊坊·八年级期末)直角三角形ABC中,,直线l过点C.
(1)当时,如图1,分别过点A、B作于点D,于点E.,,
求DE长.
(2)当,时,如图2,点B与点F关于直线l对称,连接BF,CF,动点M从点A出发,以每秒1个单位长度的速度沿AC边向终点C运动,同时动点N从点F出发,以每秒3个单位的速度沿向终点F运动,点M、N到达相应的终点时停止运动,过点M作于点D,过点N作于点E,设运动时间为t秒.
①______,当N在路径上时,______.(用含t的代数式表示)
②直接写出当与全等时t的值.
【答案】(1);(2)①;②当t=秒或5秒或秒时,△MDC与△CEN全等.
解:(1)∵AD⊥直线l, ∴∠DAC+∠ACD=90°,
∵∠ACB=90°, ∴∠BCE+∠ACD=90°, ∴∠DAC=∠ECB,
,;
, ∴△ACD≌△CBE(AAS);而,,
(2)①由题意得,AM=t,
,, 点B与点F关于直线l对称,
当N在路径上时, 故答案为:
②由轴对称的性质可知,∠BCE=∠FCE,
∵,; ,∠MCD+∠CMD=90°,∠MCD+∠BCE=90°,
∴∠NCE=∠CMD,
∴当CM=CN时,△MDC与△CEN全等,
当点N 沿F→C路径运动时,8-t=6-3t, 解得,t=-1(不合题意),
当点N 沿C→B路径运动时,此时 ; 8-t=3t-6, 解得,,
当点N 沿B→C路径运动时,此时;由题意得,8-t=18-3t, 解得,t=5,
当点N 沿C→F路径运动时,此时 ;由题意得,8-t=3t-18, 解得,,
综上所述,当t=秒或5秒或秒时,△MDC与△CEN全等.
29、(2022·内蒙古鄂尔多斯·八年级期末)【问题情境】利用角平分线构造全等三角形是常用的方法,如图1,OP平分.点A为OM上一点,过点A作,垂足为C,延长AC交ON于点B,可根据ASA证明,则,(即点C为AB的中点).
【问题探究】如图2,中,,,CD平分,,垂足E在CD的延长线上,试探究BE和CD的数量关系,并证明你的结论:
【拓展延伸】如图3,中,,,点D在线段BC上,且, 于E,DE交AB于F,试探究BE和DF之间的数量关系,并证明你的结论.
【问题探究】,证明见解析;【拓展延伸】.证明见解析【问题探究】延长BE交CA延长线于F,证明,推出,再证明,可得结论;
【拓展延伸】过点D作,交BE的延长线于点G,与AE相交于H,证明,推出,再证明得到来求解.
解:问题探究:,理由如下:
延长BE交CA延长线于F,∵CD平分,∴,
在和中,,∴,∴.,
∵,∴,∴,
在和中,,∴,∴,∴;
拓展延伸:.
证明:过点D作,交BE的延长线于点G,与AE相交于H,
∵,∴,,
∵,∴.
∵,∴,∴,
∵,∴.
∵,,∴.
∵,∴,∴,∴,
在和中,,∴;∴,
在和中,,∴
∴, ∴.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
