5.2 递归 第1课时 递归的概念与特征 课件 2022—2023学年浙教版(2019)高中信息技术选修1(25张PPT)
文档属性
| 名称 | 5.2 递归 第1课时 递归的概念与特征 课件 2022—2023学年浙教版(2019)高中信息技术选修1(25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-09-16 07:47:37 | ||
图片预览








文档简介
(共25张PPT)
递归的概念与特征
The concept and characteristics of recursion
引
入
“从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,故事讲的是从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,……”
什么是递归
What is recursion
#01
def f (n):
if n==0:
s=1
else:
s=n*f(n-1)
return s
print(f(3))
下列程序段的输出结果为____________。
简述程序执行过程
这段程序有什么特点?
当主程序执行函数f(3)时,引起第1次函数调用,进入函数后,参数n=3,应执行计算3*f (2)。
引起第2次函数调用,进入函数后,参数n=2,应执行计算2*fac(1)。……
直到计算fac(0),将引起对函数f的第4次调用。
递归的定义
大问题的解决中嵌套着与原问题相似的规模较小的问题。
这种解决问题的方式在计算机科学中称为递归,通过函数自己调用自己来实现,即一个函数在其定义中直接或间接调用自身的一种方法。
当递归到达某个边界,如问题规模缩减为0或1时,能直接得解。因此,在设计递归算法时,要满足两个条件:确定递归公式和递归结束条件。
def f (n):
if n==0:
s=1
else:
s=n*f(n-1)
return s
print(f(3))
f (3)
3*f (2)
第1次调用
第2次调用
2*f(1)
第3次调用
1*f(0)
第4次调用
1
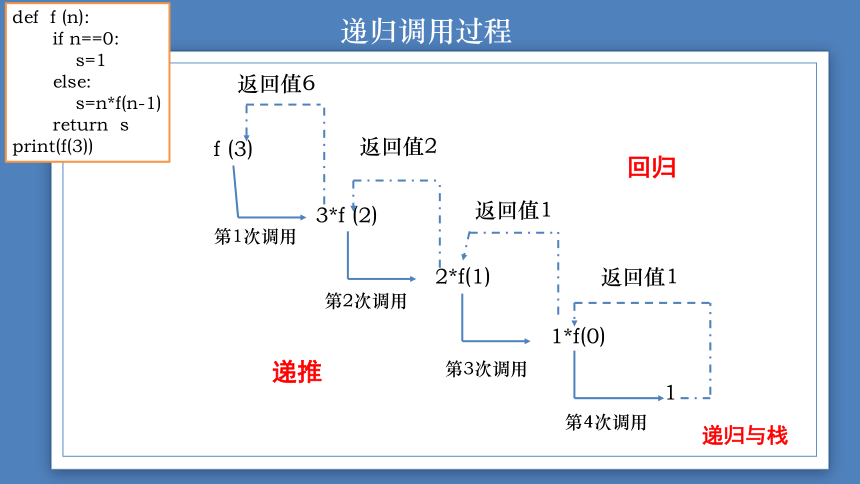
递归调用过程
返回值1
返回值1
返回值2
返回值6
递推
回归
递归与栈
递归公式
使用递归解决的问题都可以通过同一套规则转化为比该问题更为简单的子问题,这套规则被称为该问题的递归公式。
例如,在计算阶乘问题中, ( )= × ( )就是计算阶乘的递归公式。
递归结束条件
经过不断缩小问题规模,问题最终能够得以解决。在刚才的问题中, 的阶乘经过不断简化,最终转化为求解 的阶乘,而 的阶乘是我们已知的。
这种能直接得到结果,从而终止递归的情况,称为递归的结束(边界)条件。
利用递归解决问题
Use recursion to solve problems
#02
问 题
problem
academic report
presentation
在迭代中,斐波那契数列指的是这样一个数列: 1,1,2,3,5,8,13,21,34,...即从第3项开始,每一项都是前面两项的和。
请根据同学们斐波那契数列的定义,用递归算法去求解斐波那契数列的第n项,编写计算斐波那契数列的程序, 并求出斐波那契数列第45项的结果,自定义函数名为fib。
coding is fun
分析问题
递归公式与递归条件:
根据定义可知: ib( ) = ib( ) + ib( ) ≥ , ∈
当 = 或者 = 的时候 ib( ) 为 ,此时直接返回结果就可以。
与刚刚计算阶乘一样,我们可以得到以下表达式:
程序编写
def fib(n):
if n==1 or n==2:
return 1
else:
return fib(n-1)+fib(n-2)
print(f(45))
迭代程序 递归程序
f0=0 f1=1 n=2 while n<=45: f=f1+f0 f0=f1 f1=f n=n+1 print(f1) def fib (n):
if n==1 or n==2:
return 1
else:
return fib(n-1)+fib(n-2)
print(f(45))
分析这两种算法的时间复杂度。
利用递归算法求斐波那契数列,要求解fib(n),必须先计算fib(n-1)和fib(n-2),计算fib(n-1)和fib(n-2),又必须先计算fib(n-3)和fib(n-4)……以此类推,直至计算到fib(1)和fib(0),然后回归得到fib(n-1)和fib(n-2)的结果,最后得到fib(n)。递归调用的过程可以用二叉树的形式表示,如fib(5)的调用过程如下图所示。
递归调用次数即为二叉树的节点个数(深度为n的二叉树最多有2n-1个节点),即时间复杂度为O(2n)。
适用
情况
我们已经用递归算法解决了两个问题,那在什么情况下可以使用递归算法来解决问题的?
1.每次计算在规模上都有所缩小。
2.可以通过同一套规则(即相同的程序)转化为比该问题更为简单的子问题。比如:
3.问题的规模极小时必须用直接给出解答。
比如:
总结
Summarize
#03
内容梳理
递归的必要条件
递归的适用情况
递归的定义
函数的递归调用是指一个函数在它的函数体内,直接或间接地调用它自身,称为递归调用。这种函数称为递归函数。
确定递归公式
寻找递归结束条件
问题在规模小时能够直接得出答案
可以通过同一套规则转化为比该问题更为简单的子问题。
练习
#04
楼梯上有8级台阶,从下开始往上走,每次可以走一步或者两步,自定义函数fg可以计算走完n级台阶有多少种走法。实现对应功能
的Python程序如下:
def fg(n):
if n==1:
return 1
elif n==2:
return 2
else:
return fg(n-1)+fg(n-2)
Print(‘走完8级台阶的方法共有’,fg(8),‘种’)
则走完这8级台阶的走法有( )
A.34种 B.35种 C.36种 D.37种
A
问 题
problem
academic report
presentation
年龄问题
有5个人做在一起,问第5个人多大了。他说比第四个人大2岁,问第四个人多大了,他说比第三个人大2岁,问第三个人多大了,他说比第二个人大2岁,问第二个人多大了,他说比第一个人大2岁,最后问第一个人,他说他10岁了。
请大家用递归算法编写程序计算出第5个人多大了
coding is fun
递归应用 汉诺塔
#05
汉诺塔游戏
汉诺塔游戏的装置是一块铜板,上面有三根针,其中最左侧一根针上放着从大到小的n个圆盘。
游戏的目标是把所有的圆盘从最左侧一根针上移动到最右侧一根针上,中间一根针作为过渡。
游戏规定每次只能移动一个圆盘,并且大盘子不能压在小盘子上面。
启始针A
过渡针B
目标针C
一个盘子,A->C
二个盘子,2号:A->B
1号:A->C
2号:B->C
三个盘子呢?
n个盘子呢?
将n-1个盘子从A柱经过C柱移动到B柱
将A柱中剩下的一个盘子移动到C柱
将n-1个盘子从B柱经过A柱移动到C柱
n-1个看成一个整体
将n-1个盘子从A柱经过C柱移动到B柱
将A柱中剩下的一个盘子移动到C柱
将n-1个盘子从B柱经过A柱移动到C柱
【设计算法】
(1)定义一个实现盘子移动的函数move。如将n个盘子从A柱经过B柱移动到C柱,可调用函数move(n, a, b, c),其中,n表示A柱上的盘子个数,a、b、c分别表示A柱、B柱、C柱。
(3)当n=1时,直接移动盘子,递归结束。
move(n-1, a, c, b)
a→c
move(n-1, b, a, c)
【程序实现】
def move(n,a,b,c):
global s
if n==1:
s+=1
print(a,"->",c,s)
else:
move(n-1,a,c,b)
move(1,a,b,c)
move(n-1,b,a,c)
return
n=int(input("请输入盘子数:"))
s=0
move(n,"A","B","C")
递归的概念与特征
The concept and characteristics of recursion
引
入
“从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,故事讲的是从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,……”
什么是递归
What is recursion
#01
def f (n):
if n==0:
s=1
else:
s=n*f(n-1)
return s
print(f(3))
下列程序段的输出结果为____________。
简述程序执行过程
这段程序有什么特点?
当主程序执行函数f(3)时,引起第1次函数调用,进入函数后,参数n=3,应执行计算3*f (2)。
引起第2次函数调用,进入函数后,参数n=2,应执行计算2*fac(1)。……
直到计算fac(0),将引起对函数f的第4次调用。
递归的定义
大问题的解决中嵌套着与原问题相似的规模较小的问题。
这种解决问题的方式在计算机科学中称为递归,通过函数自己调用自己来实现,即一个函数在其定义中直接或间接调用自身的一种方法。
当递归到达某个边界,如问题规模缩减为0或1时,能直接得解。因此,在设计递归算法时,要满足两个条件:确定递归公式和递归结束条件。
def f (n):
if n==0:
s=1
else:
s=n*f(n-1)
return s
print(f(3))
f (3)
3*f (2)
第1次调用
第2次调用
2*f(1)
第3次调用
1*f(0)
第4次调用
1
递归调用过程
返回值1
返回值1
返回值2
返回值6
递推
回归
递归与栈
递归公式
使用递归解决的问题都可以通过同一套规则转化为比该问题更为简单的子问题,这套规则被称为该问题的递归公式。
例如,在计算阶乘问题中, ( )= × ( )就是计算阶乘的递归公式。
递归结束条件
经过不断缩小问题规模,问题最终能够得以解决。在刚才的问题中, 的阶乘经过不断简化,最终转化为求解 的阶乘,而 的阶乘是我们已知的。
这种能直接得到结果,从而终止递归的情况,称为递归的结束(边界)条件。
利用递归解决问题
Use recursion to solve problems
#02
问 题
problem
academic report
presentation
在迭代中,斐波那契数列指的是这样一个数列: 1,1,2,3,5,8,13,21,34,...即从第3项开始,每一项都是前面两项的和。
请根据同学们斐波那契数列的定义,用递归算法去求解斐波那契数列的第n项,编写计算斐波那契数列的程序, 并求出斐波那契数列第45项的结果,自定义函数名为fib。
coding is fun
分析问题
递归公式与递归条件:
根据定义可知: ib( ) = ib( ) + ib( ) ≥ , ∈
当 = 或者 = 的时候 ib( ) 为 ,此时直接返回结果就可以。
与刚刚计算阶乘一样,我们可以得到以下表达式:
程序编写
def fib(n):
if n==1 or n==2:
return 1
else:
return fib(n-1)+fib(n-2)
print(f(45))
迭代程序 递归程序
f0=0 f1=1 n=2 while n<=45: f=f1+f0 f0=f1 f1=f n=n+1 print(f1) def fib (n):
if n==1 or n==2:
return 1
else:
return fib(n-1)+fib(n-2)
print(f(45))
分析这两种算法的时间复杂度。
利用递归算法求斐波那契数列,要求解fib(n),必须先计算fib(n-1)和fib(n-2),计算fib(n-1)和fib(n-2),又必须先计算fib(n-3)和fib(n-4)……以此类推,直至计算到fib(1)和fib(0),然后回归得到fib(n-1)和fib(n-2)的结果,最后得到fib(n)。递归调用的过程可以用二叉树的形式表示,如fib(5)的调用过程如下图所示。
递归调用次数即为二叉树的节点个数(深度为n的二叉树最多有2n-1个节点),即时间复杂度为O(2n)。
适用
情况
我们已经用递归算法解决了两个问题,那在什么情况下可以使用递归算法来解决问题的?
1.每次计算在规模上都有所缩小。
2.可以通过同一套规则(即相同的程序)转化为比该问题更为简单的子问题。比如:
3.问题的规模极小时必须用直接给出解答。
比如:
总结
Summarize
#03
内容梳理
递归的必要条件
递归的适用情况
递归的定义
函数的递归调用是指一个函数在它的函数体内,直接或间接地调用它自身,称为递归调用。这种函数称为递归函数。
确定递归公式
寻找递归结束条件
问题在规模小时能够直接得出答案
可以通过同一套规则转化为比该问题更为简单的子问题。
练习
#04
楼梯上有8级台阶,从下开始往上走,每次可以走一步或者两步,自定义函数fg可以计算走完n级台阶有多少种走法。实现对应功能
的Python程序如下:
def fg(n):
if n==1:
return 1
elif n==2:
return 2
else:
return fg(n-1)+fg(n-2)
Print(‘走完8级台阶的方法共有’,fg(8),‘种’)
则走完这8级台阶的走法有( )
A.34种 B.35种 C.36种 D.37种
A
问 题
problem
academic report
presentation
年龄问题
有5个人做在一起,问第5个人多大了。他说比第四个人大2岁,问第四个人多大了,他说比第三个人大2岁,问第三个人多大了,他说比第二个人大2岁,问第二个人多大了,他说比第一个人大2岁,最后问第一个人,他说他10岁了。
请大家用递归算法编写程序计算出第5个人多大了
coding is fun
递归应用 汉诺塔
#05
汉诺塔游戏
汉诺塔游戏的装置是一块铜板,上面有三根针,其中最左侧一根针上放着从大到小的n个圆盘。
游戏的目标是把所有的圆盘从最左侧一根针上移动到最右侧一根针上,中间一根针作为过渡。
游戏规定每次只能移动一个圆盘,并且大盘子不能压在小盘子上面。
启始针A
过渡针B
目标针C
一个盘子,A->C
二个盘子,2号:A->B
1号:A->C
2号:B->C
三个盘子呢?
n个盘子呢?
将n-1个盘子从A柱经过C柱移动到B柱
将A柱中剩下的一个盘子移动到C柱
将n-1个盘子从B柱经过A柱移动到C柱
n-1个看成一个整体
将n-1个盘子从A柱经过C柱移动到B柱
将A柱中剩下的一个盘子移动到C柱
将n-1个盘子从B柱经过A柱移动到C柱
【设计算法】
(1)定义一个实现盘子移动的函数move。如将n个盘子从A柱经过B柱移动到C柱,可调用函数move(n, a, b, c),其中,n表示A柱上的盘子个数,a、b、c分别表示A柱、B柱、C柱。
(3)当n=1时,直接移动盘子,递归结束。
move(n-1, a, c, b)
a→c
move(n-1, b, a, c)
【程序实现】
def move(n,a,b,c):
global s
if n==1:
s+=1
print(a,"->",c,s)
else:
move(n-1,a,c,b)
move(1,a,b,c)
move(n-1,b,a,c)
return
n=int(input("请输入盘子数:"))
s=0
move(n,"A","B","C")
