沪科版数学七年级上册 1.4.3 有理数的加减综合 课件(共36张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 1.4.3 有理数的加减综合 课件(共36张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 256.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-17 12:32:10 | ||
图片预览








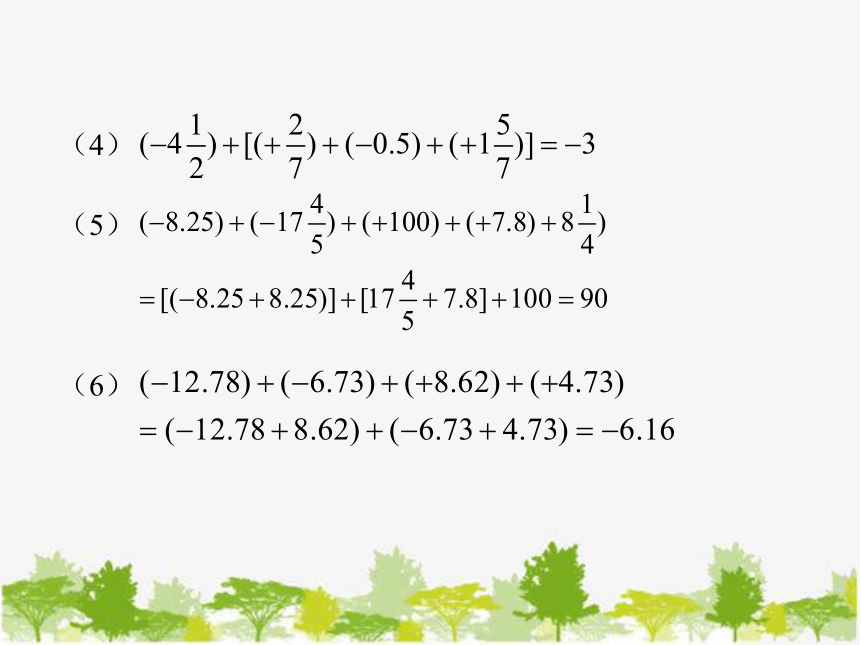



文档简介
(共37张PPT)
1.4-2 有理数的
加减综合
小明在一条东西向的跑道上,先走了20米,又走
了30米,能否确定他现在位于原来位置的哪个方向,
与原来位置相距多少米?
1. 若两次都向东,一共向东走了:( 20) ( 30) 50米 即小明位于原来位置的东方50米处
2. 若两次都向西,一共向西走了:( 20) ( 30) 50米
即小明位于原来位置的西方50米处
3. 若第一次向东走20米,第二次向西走30米, ( 20) ( 30) 10米即小明位于原来位置的西方10米处
知识回顾
4. 若第一次向西走20米,第二次向东走30米, ( 20) ( 30) 10米即小明位于原来位置的
东方10米处
5. 若第一次向西走30米,第二次向东走30米, ( 30) ( 30) 0
6. 若第一次向西走30米,第二次没走 ,
( 30) 0 30
有理数的加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不等的异号两数相加,取绝对值较大的加 数的符号,并用较大的绝对值减去较小的绝对值;
(3)互为相反数的两个数相加得零;
(4)一个数同零相加,仍得这个数.
[例1] 计算:
(1)
(2)
(3)
(4)
(5)
(6)
例题讲解
[例2] 一口水井,水面比水井口低3米,一只蜗牛从水面沿着井壁往井口爬,第一次往上爬了0.5米又往下滑了0.1米;第二次往上爬了0.42米又往下滑了0.15米;第三次往上爬了0.7米又往下滑了0.15米;第四次往上爬了0.75米又往下滑了0.1米; 第五次往上爬了0.55米,没有下滑; 第六次往上爬了0.48米.问蜗牛有没有爬出井口
解:0.5 ( 0.1) 0.42 ( 0.15) 0.7 ( 0.15) 0.75 ( 0.1) 0.55 0 0.48 2.9 3
答:蜗牛没有爬出井口.
[例3] 若 x 3 与 y 2 互为相反数,求x y的值
解: x 3 y 2 0,
x 3, y 2
x y ( 3) ( 2) 5
[例4] 计算:
(1)
(2)
(3)
(4)
(5)
(6)
[例5] 两个加数的和一定大于其中一个加数吗
答案为:不一定。
[例6] 若 a 15, b 8,且a b, 求a b
解:a 15, b= 8, a b
则 a 15, b 8,
当 a 15, b 8时, a b 23
当 a 15, b 8时, a b 7
[例7]已知
求:(1)( a) b ( c)
解:
(2)
[例8] 分别列出一个含有三个加数的满足下列条件的算式:
(1) 所有的加数都是负数,和为 13; 1 ( 2) ( 10)
(2) 一个加数为0,和为 13; ( 9) ( 4) 0
(3) 至少有一个加数是正整数,和为 13; ( 1) ( 4) ( 10)
[例9] 如图,将数字 2, 1,0,1,2,3,4,5,6,7这是个数字分别填写在五角星中每两个线的交点处(每个交点只填写一个数),将每一行上的四个数相加,共得到五个数,设a1, a2, a3, a4, a5.
则(1)a1 a2 a3 a4 a5 50
(2)交换其中任何两数的位置后, a1 a2 a3 a4 a5 的值是否改变
1
6
2
7
2
1
3
5
0
4
无论怎样交换各数的位置,按规则相加后,每个数都用了两次,a1 a2 a3 a4 a5=2( 1 2 0 1 2 3 4 5 6 7)=50
所有值不变。
答: 不变.
有理数的减法法则:
减去一个数,等于加上这个数的相反数.
知识回顾
[例1] 计算:
(1)85 27 58
(2)27 85 27 ( 85) (85 27) 58
(3)( 13) ( 21) 13 ( 21) 21 13 8
(4)( 13) ( 21) 13 ( 21) 34
(5)( 21) ( 13) 21 ( 13) (21 13) 8
(6)( 21) ( 13) 21 ( 13) 34
例题讲解
[例2] 计算:
(1) 3.2 ( 4.8) 3.2 ( 4.8) 8
(2)
(3) 0 5.6 0 ( 5.6) 5.6
(4)
[例3] 全班学生分成6个组进行游戏,每组的基分为100
分答对一题加50分,错一题扣50分.游戏结束时,各组的
分数如下:
(1) 第一名超过第二名多少分 350 200 150
(2) 第一名超过第六名多少分 350 ( 200) 350 200 550
第一组 第二组 第三组 第四组 第五组 第六组
200 50 350 200 100 150
[例4] 某日长春等5个城市的最高气温与最低气温记录如下:
问: 哪个城市的温差最大 哈尔滨
哪个城市的温差最小 大连
城市 哈尔滨 长春 沈阳 北京 大连
最高气温 2 3 3 12 6
最低气温 12 10 8 2 2
[例5] 下表列出国外几个城市与北京的时差(带正号的数
表示同一时刻比北京时间早的时数)
(1) 如果现在的北京时间是中午
12:00, 那么东京时间是多少
12 1 13
(2) 如果小芳给远在纽约的舅舅打电话,她在北京时间下午14:00打电话,你认为合适吗
答案:14 ( 13) 1 不合适
城市 时差
纽约 13
巴黎 7
东京 1
[例6]计算 11 7 9 6
解原式 11 ( 7) ( 9) 6
27 6
21
[例7] 已知 a 4, b 5, c 7,求代数式 a b c的值.
解: 原式 a b c ( 4) ( 5) ( 7) 8
[例8]若a 0, b 0, 试求 a b 1 b a 1 的值
解: a b 1 b a 1
a b 1 [ (b a 1)]
a b 1 b a 1
0
[例9]
(1) 两个负数的和为a,他们的差为b, 则a与b的大小关 系是( )
A. a b B. a b C. a b D. a b
(2) 已知b 0,a 0,则a,a b,a+b的大小关系是 ( )
A. a a b a b B. a b a a b
C. a b a b a D. a b a a b
[例10]点A,B在数轴上分别是表示有理数a,b, A,B两
点间的距离表示为 AB a b
回答下列问题:
(1)数轴上表示2和5的两点间的距离是 2 5 3
(2)数轴上表示 2和 5的两点间的距离是
2 ( 5) 3
(3)数轴上表示1和 3的两点间的距离是 1 ( 3) 4
(4)数轴上表示x和 1的两点间的距离是 x 1 , 如果
AB 2,那么x 1或 3
[例11] 设(x) 表示不超过数x的整数中最大的整数,例如 (2.53) 2, ( 1.3) 2,根据此规定,试做下列运算:
(1) (5.3) (3) 5 3 8
(2) ( 4.3) ( ) 5 0 5
(3) ( ) ( 1 ) 0 ( 2) 2
(4) (0) ( 2.7) 0 ( 3) 3
1.有理数加减法统一成加法的意义
(1)有理数加减混合运算,可以通过有理数减法法则将减 法转化为加法,统一成只有加法运算的和式,
如 ( 12) ( 8) ( 6) ( 5) ( 12) ( 8) ( 6) ( 5)
(2)在和式里,通常把各个加数的括号和它前面的加号省l略不写,写成省略加号的和的形式:
如 ( 12) ( 8) ( 6) ( 5) 12 8 6 5
(3)和式的读法,一是按这个式子表示的意义,读作" 12, 8, 6, 5的和〃;
二是按运算的意义,读作"负12,减8,减6,加5〃.
知识回顾
2.有理数加减混合运算的方法和步骤:
(1)将有理数加减法统一成加法,然后省略括号和加号
(2)运用加法法则,加法运算律进行简便运算
[例1] 计算 :( 10) ( 13) ( 4) ( 9) 6
解原式 10 ( 13) ( 4) ( 9) 6
12
例题讲解
[例2] 计算
解:原式
[例3] 把
算式省略加号代数和,并计算出结果.
解算式
[例4] 填空
(1)比 小2的数是_________,比 大3的数是 ___________.
(2)6 x y 的最大值___, 此时 x与y是什么关系____
(3)如果 a 4, b 8,a与b异号,
则a b ____
[例5] 填空
(1)比 小2的数是___________,比 大 3的数是
__________.
(2)6 x y 的最大值是6 , 此时 x与y是什么关系 x y .
(3)如果 a 4, b 8,a与b异号,
则a b 12, 12 .
[例6] 求值: 若a与 3 的相反数的和为 1, b的绝对值等于2, c 6 ,求代数式 a b c的值
解: a 3 1, a 4, b 2, b 2
a b c 4 2 6 12
a b c 4 2 6 8
[例7] 你能找到三个整数a,b,c,使得关系式 (a b c) (a b c) (a b c) ( a b c) 3388成立吗
如果能找到,请你举出一例;如果找不到,请你说明理由.
解: 不妨设 a b c 为偶数.
则 a b c (a b c) 2b 为偶数
a b c (a b c) 2c 为偶数
a b c (a b c) 2a 为偶数
∴ (a b c) (a b c) (a b c) ( a b c) 能被16整除,而3388 不能被16整除.
1.4-2 有理数的
加减综合
小明在一条东西向的跑道上,先走了20米,又走
了30米,能否确定他现在位于原来位置的哪个方向,
与原来位置相距多少米?
1. 若两次都向东,一共向东走了:( 20) ( 30) 50米 即小明位于原来位置的东方50米处
2. 若两次都向西,一共向西走了:( 20) ( 30) 50米
即小明位于原来位置的西方50米处
3. 若第一次向东走20米,第二次向西走30米, ( 20) ( 30) 10米即小明位于原来位置的西方10米处
知识回顾
4. 若第一次向西走20米,第二次向东走30米, ( 20) ( 30) 10米即小明位于原来位置的
东方10米处
5. 若第一次向西走30米,第二次向东走30米, ( 30) ( 30) 0
6. 若第一次向西走30米,第二次没走 ,
( 30) 0 30
有理数的加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不等的异号两数相加,取绝对值较大的加 数的符号,并用较大的绝对值减去较小的绝对值;
(3)互为相反数的两个数相加得零;
(4)一个数同零相加,仍得这个数.
[例1] 计算:
(1)
(2)
(3)
(4)
(5)
(6)
例题讲解
[例2] 一口水井,水面比水井口低3米,一只蜗牛从水面沿着井壁往井口爬,第一次往上爬了0.5米又往下滑了0.1米;第二次往上爬了0.42米又往下滑了0.15米;第三次往上爬了0.7米又往下滑了0.15米;第四次往上爬了0.75米又往下滑了0.1米; 第五次往上爬了0.55米,没有下滑; 第六次往上爬了0.48米.问蜗牛有没有爬出井口
解:0.5 ( 0.1) 0.42 ( 0.15) 0.7 ( 0.15) 0.75 ( 0.1) 0.55 0 0.48 2.9 3
答:蜗牛没有爬出井口.
[例3] 若 x 3 与 y 2 互为相反数,求x y的值
解: x 3 y 2 0,
x 3, y 2
x y ( 3) ( 2) 5
[例4] 计算:
(1)
(2)
(3)
(4)
(5)
(6)
[例5] 两个加数的和一定大于其中一个加数吗
答案为:不一定。
[例6] 若 a 15, b 8,且a b, 求a b
解:a 15, b= 8, a b
则 a 15, b 8,
当 a 15, b 8时, a b 23
当 a 15, b 8时, a b 7
[例7]已知
求:(1)( a) b ( c)
解:
(2)
[例8] 分别列出一个含有三个加数的满足下列条件的算式:
(1) 所有的加数都是负数,和为 13; 1 ( 2) ( 10)
(2) 一个加数为0,和为 13; ( 9) ( 4) 0
(3) 至少有一个加数是正整数,和为 13; ( 1) ( 4) ( 10)
[例9] 如图,将数字 2, 1,0,1,2,3,4,5,6,7这是个数字分别填写在五角星中每两个线的交点处(每个交点只填写一个数),将每一行上的四个数相加,共得到五个数,设a1, a2, a3, a4, a5.
则(1)a1 a2 a3 a4 a5 50
(2)交换其中任何两数的位置后, a1 a2 a3 a4 a5 的值是否改变
1
6
2
7
2
1
3
5
0
4
无论怎样交换各数的位置,按规则相加后,每个数都用了两次,a1 a2 a3 a4 a5=2( 1 2 0 1 2 3 4 5 6 7)=50
所有值不变。
答: 不变.
有理数的减法法则:
减去一个数,等于加上这个数的相反数.
知识回顾
[例1] 计算:
(1)85 27 58
(2)27 85 27 ( 85) (85 27) 58
(3)( 13) ( 21) 13 ( 21) 21 13 8
(4)( 13) ( 21) 13 ( 21) 34
(5)( 21) ( 13) 21 ( 13) (21 13) 8
(6)( 21) ( 13) 21 ( 13) 34
例题讲解
[例2] 计算:
(1) 3.2 ( 4.8) 3.2 ( 4.8) 8
(2)
(3) 0 5.6 0 ( 5.6) 5.6
(4)
[例3] 全班学生分成6个组进行游戏,每组的基分为100
分答对一题加50分,错一题扣50分.游戏结束时,各组的
分数如下:
(1) 第一名超过第二名多少分 350 200 150
(2) 第一名超过第六名多少分 350 ( 200) 350 200 550
第一组 第二组 第三组 第四组 第五组 第六组
200 50 350 200 100 150
[例4] 某日长春等5个城市的最高气温与最低气温记录如下:
问: 哪个城市的温差最大 哈尔滨
哪个城市的温差最小 大连
城市 哈尔滨 长春 沈阳 北京 大连
最高气温 2 3 3 12 6
最低气温 12 10 8 2 2
[例5] 下表列出国外几个城市与北京的时差(带正号的数
表示同一时刻比北京时间早的时数)
(1) 如果现在的北京时间是中午
12:00, 那么东京时间是多少
12 1 13
(2) 如果小芳给远在纽约的舅舅打电话,她在北京时间下午14:00打电话,你认为合适吗
答案:14 ( 13) 1 不合适
城市 时差
纽约 13
巴黎 7
东京 1
[例6]计算 11 7 9 6
解原式 11 ( 7) ( 9) 6
27 6
21
[例7] 已知 a 4, b 5, c 7,求代数式 a b c的值.
解: 原式 a b c ( 4) ( 5) ( 7) 8
[例8]若a 0, b 0, 试求 a b 1 b a 1 的值
解: a b 1 b a 1
a b 1 [ (b a 1)]
a b 1 b a 1
0
[例9]
(1) 两个负数的和为a,他们的差为b, 则a与b的大小关 系是( )
A. a b B. a b C. a b D. a b
(2) 已知b 0,a 0,则a,a b,a+b的大小关系是 ( )
A. a a b a b B. a b a a b
C. a b a b a D. a b a a b
[例10]点A,B在数轴上分别是表示有理数a,b, A,B两
点间的距离表示为 AB a b
回答下列问题:
(1)数轴上表示2和5的两点间的距离是 2 5 3
(2)数轴上表示 2和 5的两点间的距离是
2 ( 5) 3
(3)数轴上表示1和 3的两点间的距离是 1 ( 3) 4
(4)数轴上表示x和 1的两点间的距离是 x 1 , 如果
AB 2,那么x 1或 3
[例11] 设(x) 表示不超过数x的整数中最大的整数,例如 (2.53) 2, ( 1.3) 2,根据此规定,试做下列运算:
(1) (5.3) (3) 5 3 8
(2) ( 4.3) ( ) 5 0 5
(3) ( ) ( 1 ) 0 ( 2) 2
(4) (0) ( 2.7) 0 ( 3) 3
1.有理数加减法统一成加法的意义
(1)有理数加减混合运算,可以通过有理数减法法则将减 法转化为加法,统一成只有加法运算的和式,
如 ( 12) ( 8) ( 6) ( 5) ( 12) ( 8) ( 6) ( 5)
(2)在和式里,通常把各个加数的括号和它前面的加号省l略不写,写成省略加号的和的形式:
如 ( 12) ( 8) ( 6) ( 5) 12 8 6 5
(3)和式的读法,一是按这个式子表示的意义,读作" 12, 8, 6, 5的和〃;
二是按运算的意义,读作"负12,减8,减6,加5〃.
知识回顾
2.有理数加减混合运算的方法和步骤:
(1)将有理数加减法统一成加法,然后省略括号和加号
(2)运用加法法则,加法运算律进行简便运算
[例1] 计算 :( 10) ( 13) ( 4) ( 9) 6
解原式 10 ( 13) ( 4) ( 9) 6
12
例题讲解
[例2] 计算
解:原式
[例3] 把
算式省略加号代数和,并计算出结果.
解算式
[例4] 填空
(1)比 小2的数是_________,比 大3的数是 ___________.
(2)6 x y 的最大值___, 此时 x与y是什么关系____
(3)如果 a 4, b 8,a与b异号,
则a b ____
[例5] 填空
(1)比 小2的数是___________,比 大 3的数是
__________.
(2)6 x y 的最大值是6 , 此时 x与y是什么关系 x y .
(3)如果 a 4, b 8,a与b异号,
则a b 12, 12 .
[例6] 求值: 若a与 3 的相反数的和为 1, b的绝对值等于2, c 6 ,求代数式 a b c的值
解: a 3 1, a 4, b 2, b 2
a b c 4 2 6 12
a b c 4 2 6 8
[例7] 你能找到三个整数a,b,c,使得关系式 (a b c) (a b c) (a b c) ( a b c) 3388成立吗
如果能找到,请你举出一例;如果找不到,请你说明理由.
解: 不妨设 a b c 为偶数.
则 a b c (a b c) 2b 为偶数
a b c (a b c) 2c 为偶数
a b c (a b c) 2a 为偶数
∴ (a b c) (a b c) (a b c) ( a b c) 能被16整除,而3388 不能被16整除.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
