11.1.2 三角形的高、中线与角平分线(含三角形的稳定性) 课件(共27张PPT)
文档属性
| 名称 | 11.1.2 三角形的高、中线与角平分线(含三角形的稳定性) 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 06:07:05 | ||
图片预览







文档简介
(共27张PPT)
人教版 八年级上册
11.1与三角形有关的线段
11.1.2 三角形的高、中线与角平分线
11.1.3 三角形的稳定性
情景导入
想一想
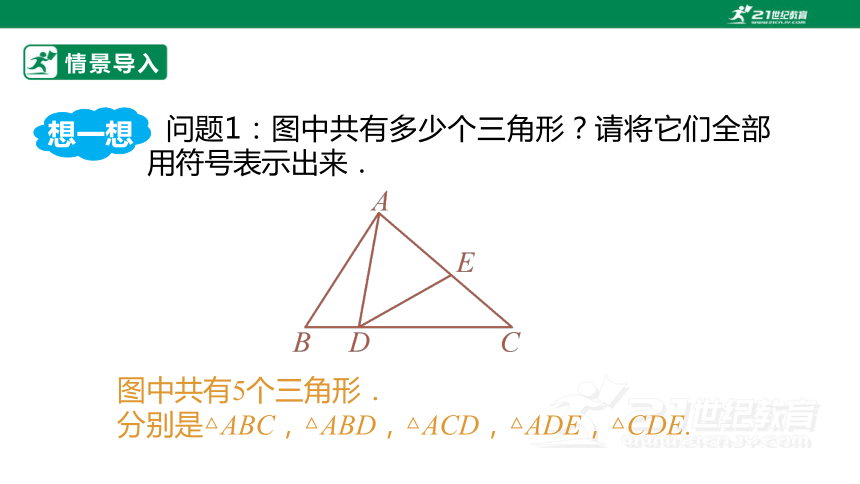
问题1:图中共有多少个三角形?请将它们全部用符号表示出来.
图中共有5个三角形.
分别是△ABC,△ABD,△ACD,△ADE,△CDE.
想一想
问题2:利用长为2 cm,3 cm,4 cm,5 cm的四条线段可以组成几个三角形?为什么?
答:可以组成3个三角形.从四条线段中任选三条,共有四种选法:
①2 cm,3 cm,4 cm;
②3 cm,4 cm,5 cm;
③2 cm,3 cm,5 cm;
④2 cm,4 cm,5 cm.
其中满足“三角形两边之和大于第三边”的只有第①,②,④这三组.
垂线的定义: 当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直, 其中一条直线叫做另一条直线的垂线.
线段中点的定义: 把一条线段分成两条相等的线段的点.
角平分线的定义: 一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
温故
合作探究
知识板块一 三角形的高
你还记得 “过一点画已知直线的垂线”吗
你能过三角形的一个顶点,你能画出它的对边的垂线吗
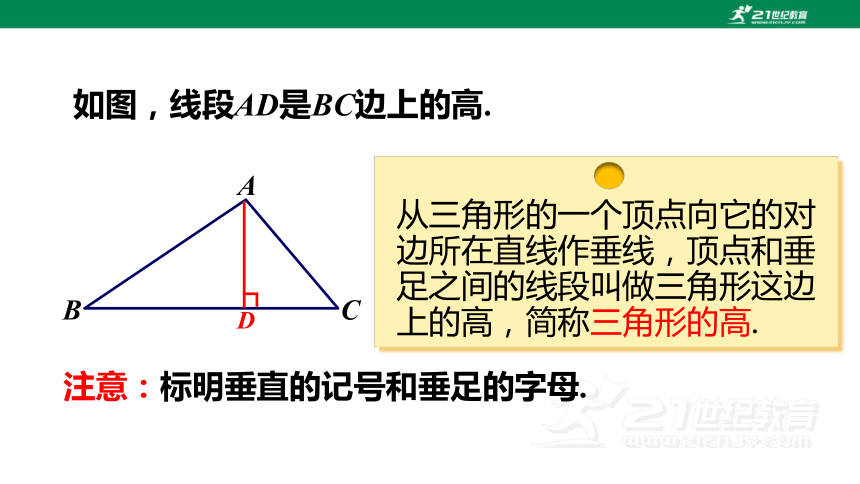
如图,线段AD是BC边上的高.
注意:标明垂直的记号和垂足的字母.
B
A
C
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高.
D
锐角三角形的三条高
每人画一个锐角三角形.
(1) 你能画出这个三角形的三条高吗
(2) 这三条高之间有怎样的位置关系?
O
锐角三角形的三条高是在三角形的内部还是外部
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
直角三角形的三条高
在纸上画出一个直角三角形.
A
B
C
(1)画出直角三角形的三条高.
直角边BC边上的高是______;
AB
直角边AB边上的高是______;
CB
(2)它们有怎样的位置关系?
D
斜边AC边上的高是_______.
BD
●
直角三角形的三条高交于直角顶点.
钝角三角形的三条高
(1) 钝角三角形的三条高交于一点吗?
(2)它们所在的直线交于一点吗?
A
B
C
想一想
作钝角△ABC的高
①作BC边上的高,延长CB,过点A作AD BC于D
②作AB边上的高,延长AB,过点C作CE AB于E
③作AC边上的高,过点B作BF AC于F
结论:钝角三角形的三条高不相交于一点.
钝角三角形的三条高所在直线交于一点.
A
B
C
D
E
F
O
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角
三角形
直角
三角形
锐角
三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形
内部
直角顶点
三角形
外部
合作探究
知识板块二 三角形的中线
用同样方法, 你能画出△ABC 的另两条边上的中线吗?
B
A
C
D
·
如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做 △ABC的边BC上的中线.
如图,三角形的三条中线相交于一点.三角形三
条中线的交点叫做三角形的重心.
B
A
C
D
E
F
·
取一块质地均匀的三角形木板,顶住三条中线的交点,木板会保持平衡,这个平衡点就是这块三角形木板的重心.
合作探究
知识板块三 三角形的角平分线
如果现在你手上有一张画着一个三角形的薄纸,你能想几种办法画出它的一个内角的平分线?
如图,在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
A
B
C
D
●
●
︶
︶
1
2
因为AD是△ABC的角平分线,
所以∠BAD =∠CAD =
∠BAC.
三角形的三条角平分线相交于一点,交点在三角形的内部.
合作探究
知识板块四 三角形的稳定性
盖房子时,在窗框安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?我们来探究下面的问题.
(1)如图,将三根木条用钉子
钉成一个三角形木架,然
后扭动它,它的形状会改
变吗?
1.三角形的稳定性
(2)如图,将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
(3)如图,在四边形木架上再钉一根木条,将它的一对不相邻的顶点连接起来,然后再扭动它,
这时木架的形状还会改变吗?
可以发现,三角形木架的形状不会改变,而四
边形木架的形状会改变.
这就是说,三角形是具有稳定性的图形,而四
边形没有稳定性.
2.三角形稳定性的实际应用
三角形的稳定性有广泛的应用,如图表示其中一些例子.你能再举一 些例子吗?
钢架桥
起重机
四边形的不稳定性也有广泛的应用,如图表示其中一些例子.
当堂演练
1.在直角三角形中,有两条高是它的________,另一条高在这个三角形的________.锐角三角形的三条高的交点在______________,直角三角形的三条高的交点在____________________,钝角三角形的三条高所在直线的交点在_______________.
直角边
内部
三角形的内部
两直角边的交点处
三角形的外部
2.如图,AD, BE, CF是△ ABC的三条角平分线,则∠1+ ∠1 + ∠3=_____.
B
C
︶
︶
1
2
D
E
F
A
︶
3
90°
3.三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
B
4.如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是( )
A.2 B.3 C.6 D.不能确定
A
5.下列图形中具有稳定性的是( )
A.①②③④ B.①③
C.②④ D.①②③
B
板书设计
1.三角形的高、中线、角平分线的性质.
2.三角形的稳定性
人教版 八年级上册
11.1与三角形有关的线段
11.1.2 三角形的高、中线与角平分线
11.1.3 三角形的稳定性
情景导入
想一想
问题1:图中共有多少个三角形?请将它们全部用符号表示出来.
图中共有5个三角形.
分别是△ABC,△ABD,△ACD,△ADE,△CDE.
想一想
问题2:利用长为2 cm,3 cm,4 cm,5 cm的四条线段可以组成几个三角形?为什么?
答:可以组成3个三角形.从四条线段中任选三条,共有四种选法:
①2 cm,3 cm,4 cm;
②3 cm,4 cm,5 cm;
③2 cm,3 cm,5 cm;
④2 cm,4 cm,5 cm.
其中满足“三角形两边之和大于第三边”的只有第①,②,④这三组.
垂线的定义: 当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直, 其中一条直线叫做另一条直线的垂线.
线段中点的定义: 把一条线段分成两条相等的线段的点.
角平分线的定义: 一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
温故
合作探究
知识板块一 三角形的高
你还记得 “过一点画已知直线的垂线”吗
你能过三角形的一个顶点,你能画出它的对边的垂线吗
如图,线段AD是BC边上的高.
注意:标明垂直的记号和垂足的字母.
B
A
C
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高.
D
锐角三角形的三条高
每人画一个锐角三角形.
(1) 你能画出这个三角形的三条高吗
(2) 这三条高之间有怎样的位置关系?
O
锐角三角形的三条高是在三角形的内部还是外部
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
直角三角形的三条高
在纸上画出一个直角三角形.
A
B
C
(1)画出直角三角形的三条高.
直角边BC边上的高是______;
AB
直角边AB边上的高是______;
CB
(2)它们有怎样的位置关系?
D
斜边AC边上的高是_______.
BD
●
直角三角形的三条高交于直角顶点.
钝角三角形的三条高
(1) 钝角三角形的三条高交于一点吗?
(2)它们所在的直线交于一点吗?
A
B
C
想一想
作钝角△ABC的高
①作BC边上的高,延长CB,过点A作AD BC于D
②作AB边上的高,延长AB,过点C作CE AB于E
③作AC边上的高,过点B作BF AC于F
结论:钝角三角形的三条高不相交于一点.
钝角三角形的三条高所在直线交于一点.
A
B
C
D
E
F
O
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角
三角形
直角
三角形
锐角
三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形
内部
直角顶点
三角形
外部
合作探究
知识板块二 三角形的中线
用同样方法, 你能画出△ABC 的另两条边上的中线吗?
B
A
C
D
·
如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做 △ABC的边BC上的中线.
如图,三角形的三条中线相交于一点.三角形三
条中线的交点叫做三角形的重心.
B
A
C
D
E
F
·
取一块质地均匀的三角形木板,顶住三条中线的交点,木板会保持平衡,这个平衡点就是这块三角形木板的重心.
合作探究
知识板块三 三角形的角平分线
如果现在你手上有一张画着一个三角形的薄纸,你能想几种办法画出它的一个内角的平分线?
如图,在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
A
B
C
D
●
●
︶
︶
1
2
因为AD是△ABC的角平分线,
所以∠BAD =∠CAD =
∠BAC.
三角形的三条角平分线相交于一点,交点在三角形的内部.
合作探究
知识板块四 三角形的稳定性
盖房子时,在窗框安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?我们来探究下面的问题.
(1)如图,将三根木条用钉子
钉成一个三角形木架,然
后扭动它,它的形状会改
变吗?
1.三角形的稳定性
(2)如图,将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
(3)如图,在四边形木架上再钉一根木条,将它的一对不相邻的顶点连接起来,然后再扭动它,
这时木架的形状还会改变吗?
可以发现,三角形木架的形状不会改变,而四
边形木架的形状会改变.
这就是说,三角形是具有稳定性的图形,而四
边形没有稳定性.
2.三角形稳定性的实际应用
三角形的稳定性有广泛的应用,如图表示其中一些例子.你能再举一 些例子吗?
钢架桥
起重机
四边形的不稳定性也有广泛的应用,如图表示其中一些例子.
当堂演练
1.在直角三角形中,有两条高是它的________,另一条高在这个三角形的________.锐角三角形的三条高的交点在______________,直角三角形的三条高的交点在____________________,钝角三角形的三条高所在直线的交点在_______________.
直角边
内部
三角形的内部
两直角边的交点处
三角形的外部
2.如图,AD, BE, CF是△ ABC的三条角平分线,则∠1+ ∠1 + ∠3=_____.
B
C
︶
︶
1
2
D
E
F
A
︶
3
90°
3.三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
B
4.如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是( )
A.2 B.3 C.6 D.不能确定
A
5.下列图形中具有稳定性的是( )
A.①②③④ B.①③
C.②④ D.①②③
B
板书设计
1.三角形的高、中线、角平分线的性质.
2.三角形的稳定性
