24.3.4相似三角形的应用(1)学案
文档属性
| 名称 | 24.3.4相似三角形的应用(1)学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 66.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-16 00:00:00 | ||
图片预览

文档简介
课 题:相似三角形的应用(1)
测量物体的高度
序 号:( 11 )
年 级: 九年级 单元名称:第24章相似图形的性质
课 型: 新授课 上课时间:
学习内容:华东师大版课本62页例6
学习目标:1.进一步巩固相似三角形的知识.
2.能够运用三角形相似的知识,解决不能直接测量物体的高度
重 点:运用三角形相似的知识计算不能直接测量物体的高度.
难 点:如何把实际问题抽象为数学问题
学法指导:合作探究
学 习 过 程
自主预习课本62页例6,完成下题:
在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为90米,那么高楼的高度是多少米 (在同一时刻物体的高度与它的影长成正比例.)
相似三角形的性质有哪些?
探究一:利用太阳光的影子,来测量物体高度
在一个风和日丽的周末下午,付平、治国、王宁一行三人组成数学实践小组,他们带着一根2米长的竹竿和一根皮尺准备测量学校的教学楼的高度和国旗旗杆的高度。
问题1:首先他们来到教学楼前,付平将所带的竹竿直立的竖在地面上,治国和王宁用皮尺测得教学楼在地面上的影长为10米,竹竿的影长为1.5米。付平说这样就可以计算学校的教学楼的高度了,你知道他是怎么计算的吗?
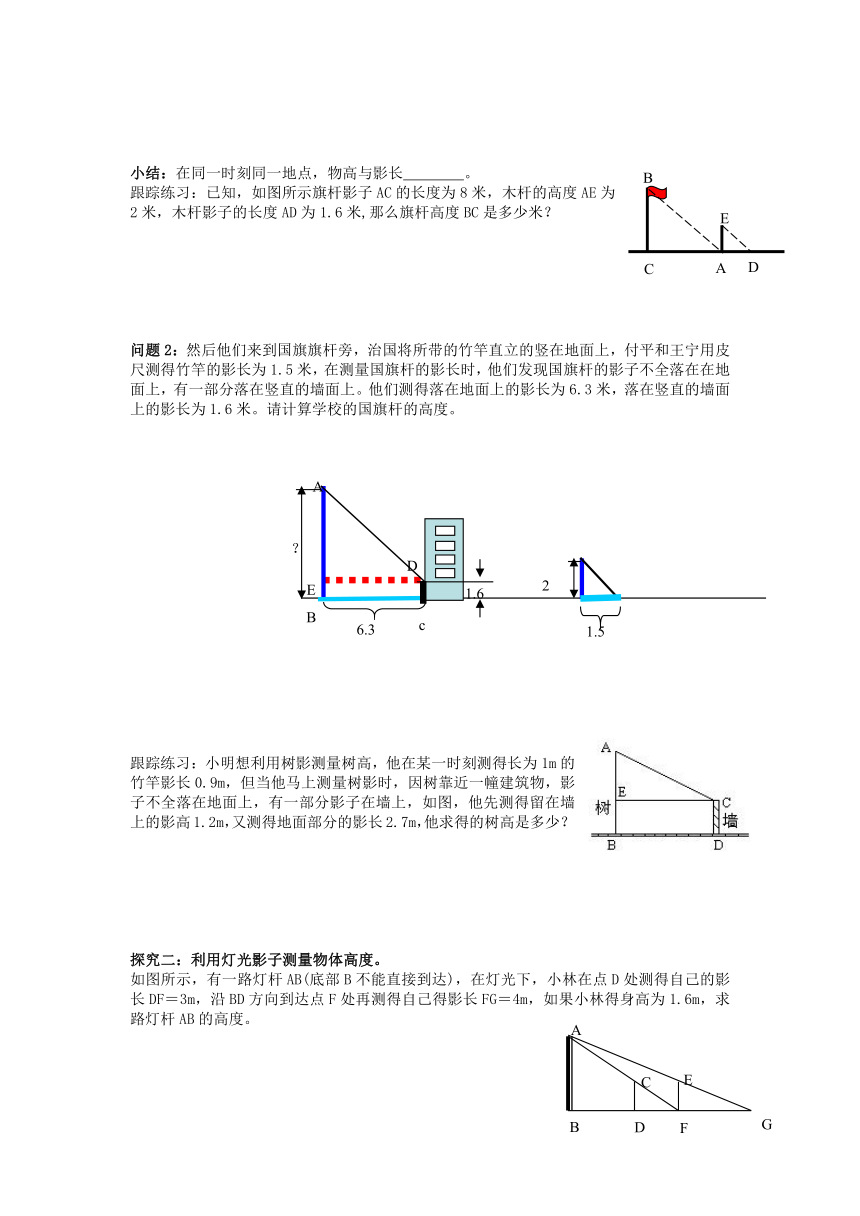
小结:在同一时刻同一地点,物高与影长 。
跟踪练习:已知,如图所示旗杆影子AC的长度为8米,木杆的高度AE为
2米,木杆影子的长度AD为1.6米,那么旗杆高度BC是多少米?
问题2:然后他们来到国旗旗杆旁,治国将所带的竹竿直立的竖在地面上,付平和王宁用皮尺测得竹竿的影长为1.5米,在测量国旗杆的影长时,他们发现国旗杆的影子不全落在在地面上,有一部分落在竖直的墙面上。他们测得落在地面上的影长为6.3米,落在竖直的墙面上的影长为1.6米。请计算学校的国旗杆的高度。
跟踪练习:小明想利用树影测量树高,他在某一时刻测得长为1m的竹竿影长0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,如图,他先测得留在墙上的影高1.2m,又测得地面部分的影长2.7m,他求得的树高是多少?
探究二:利用灯光影子测量物体高度。
如图所示,有一路灯杆AB(底部B不能直接到达),在灯光下,小林在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己得影长FG=4m,如果小林得身高为1.6m,求路灯杆AB的高度。
跟踪练习:已知左、右并排的两棵大树的高分别是AB = 8 m和CD = 12 m,两树根部的距离BD = 5 m.一个目高1.6 m的人沿着正对这两棵树的一条水平直路m从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C ?
探究三:用平面镜成像测量物体高度。
小玉用下面的方法来测量学校教学大楼AB的高度.如图所示,在水平地面上放一面平面镜,镜子与教学大楼的距离EA=21米,当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B,且已知她的眼睛距地面高度DC=1.6米,请你帮助小玉计算出教学大楼的高度AB是多少米?
跟踪练习:龙龙和泉泉两人来到了一座古塔前,龙龙站在古塔前从一小块积水处看到塔顶的倒影,这时泉泉测得积水处C距龙龙CE为2米,龙龙的眼部离地面的高度DE是1.5米,塔底中心B到积水处C的距离是40米.求塔高AB。
1.一根1.5米长的标杆直立在水平地面上,它在阳光下的影长为2.1米;此时一棵水杉树的影长为10.5米,这棵水杉树高为 ( )
A.7.5米 B.8米 C.14.7米 D.15.75米
2.晚上,小华出去散步,在经过一盏路灯时,他发现自己的身影是 ( )
A.变长 B.变短 C.先变长后变短 D.先变短后变长
3.已知,如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
4.如图,某测量工作人员的眼睛A与标杆顶端F、电视塔顶端E在同一直线上,已知此人眼睛距地面1.6米,标杆为3.2米,且BC=1米,CD=5米,求电视塔的高ED。
5.小明在某一时刻测得1m的杆子在阳光下的影子长为2m,他想测量电线杆AB的高度,但其影子恰好落在土坡的坡面CD和地面BC上,量得CD=2m,BC=10m,CD与地面成45°,求电线杆的高度.
预 习 检 测
课 前 准 备
交 流 合 作
1.5米
10米
A
B
C
D
E
F
B
A
C
E
D
E
D
6.3
1.5
1.6
?
2
A
B
c
G
C
E
D
F
B
A
F
A
B
C
D
m
E
A
D
E
B
C
M
达 标 检 测
A
D
C
E
B
B
C
F
A
D
E
课 后 反 思
测量物体的高度
序 号:( 11 )
年 级: 九年级 单元名称:第24章相似图形的性质
课 型: 新授课 上课时间:
学习内容:华东师大版课本62页例6
学习目标:1.进一步巩固相似三角形的知识.
2.能够运用三角形相似的知识,解决不能直接测量物体的高度
重 点:运用三角形相似的知识计算不能直接测量物体的高度.
难 点:如何把实际问题抽象为数学问题
学法指导:合作探究
学 习 过 程
自主预习课本62页例6,完成下题:
在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为90米,那么高楼的高度是多少米 (在同一时刻物体的高度与它的影长成正比例.)
相似三角形的性质有哪些?
探究一:利用太阳光的影子,来测量物体高度
在一个风和日丽的周末下午,付平、治国、王宁一行三人组成数学实践小组,他们带着一根2米长的竹竿和一根皮尺准备测量学校的教学楼的高度和国旗旗杆的高度。
问题1:首先他们来到教学楼前,付平将所带的竹竿直立的竖在地面上,治国和王宁用皮尺测得教学楼在地面上的影长为10米,竹竿的影长为1.5米。付平说这样就可以计算学校的教学楼的高度了,你知道他是怎么计算的吗?
小结:在同一时刻同一地点,物高与影长 。
跟踪练习:已知,如图所示旗杆影子AC的长度为8米,木杆的高度AE为
2米,木杆影子的长度AD为1.6米,那么旗杆高度BC是多少米?
问题2:然后他们来到国旗旗杆旁,治国将所带的竹竿直立的竖在地面上,付平和王宁用皮尺测得竹竿的影长为1.5米,在测量国旗杆的影长时,他们发现国旗杆的影子不全落在在地面上,有一部分落在竖直的墙面上。他们测得落在地面上的影长为6.3米,落在竖直的墙面上的影长为1.6米。请计算学校的国旗杆的高度。
跟踪练习:小明想利用树影测量树高,他在某一时刻测得长为1m的竹竿影长0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,如图,他先测得留在墙上的影高1.2m,又测得地面部分的影长2.7m,他求得的树高是多少?
探究二:利用灯光影子测量物体高度。
如图所示,有一路灯杆AB(底部B不能直接到达),在灯光下,小林在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己得影长FG=4m,如果小林得身高为1.6m,求路灯杆AB的高度。
跟踪练习:已知左、右并排的两棵大树的高分别是AB = 8 m和CD = 12 m,两树根部的距离BD = 5 m.一个目高1.6 m的人沿着正对这两棵树的一条水平直路m从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C ?
探究三:用平面镜成像测量物体高度。
小玉用下面的方法来测量学校教学大楼AB的高度.如图所示,在水平地面上放一面平面镜,镜子与教学大楼的距离EA=21米,当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B,且已知她的眼睛距地面高度DC=1.6米,请你帮助小玉计算出教学大楼的高度AB是多少米?
跟踪练习:龙龙和泉泉两人来到了一座古塔前,龙龙站在古塔前从一小块积水处看到塔顶的倒影,这时泉泉测得积水处C距龙龙CE为2米,龙龙的眼部离地面的高度DE是1.5米,塔底中心B到积水处C的距离是40米.求塔高AB。
1.一根1.5米长的标杆直立在水平地面上,它在阳光下的影长为2.1米;此时一棵水杉树的影长为10.5米,这棵水杉树高为 ( )
A.7.5米 B.8米 C.14.7米 D.15.75米
2.晚上,小华出去散步,在经过一盏路灯时,他发现自己的身影是 ( )
A.变长 B.变短 C.先变长后变短 D.先变短后变长
3.已知,如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
4.如图,某测量工作人员的眼睛A与标杆顶端F、电视塔顶端E在同一直线上,已知此人眼睛距地面1.6米,标杆为3.2米,且BC=1米,CD=5米,求电视塔的高ED。
5.小明在某一时刻测得1m的杆子在阳光下的影子长为2m,他想测量电线杆AB的高度,但其影子恰好落在土坡的坡面CD和地面BC上,量得CD=2m,BC=10m,CD与地面成45°,求电线杆的高度.
预 习 检 测
课 前 准 备
交 流 合 作
1.5米
10米
A
B
C
D
E
F
B
A
C
E
D
E
D
6.3
1.5
1.6
?
2
A
B
c
G
C
E
D
F
B
A
F
A
B
C
D
m
E
A
D
E
B
C
M
达 标 检 测
A
D
C
E
B
B
C
F
A
D
E
课 后 反 思
