24.3.4相似三角形的应用(2)学案
文档属性
| 名称 | 24.3.4相似三角形的应用(2)学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 56.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-16 13:12:55 | ||
图片预览

文档简介
课 题:相似三角形的应用(2)
测量物体宽度问题
序 号:( 12 )
年 级: 九年级 单元名称:第24章相似图形的性质
课 型: 新授课 上课时间:
学习内容:华东师大版课本62----63 页 例7
学习目标:1.进一步巩固相似三角形的知识.
2.能够运用三角形相似的知识,解决不能直接测量物体的度宽问题。
重 点:运用三角形相似的知识计算不能直接测量物体的宽度问题.
难 点:如何把实际问题抽象为数学问题
学法指导:合作探究
学 习 过 程
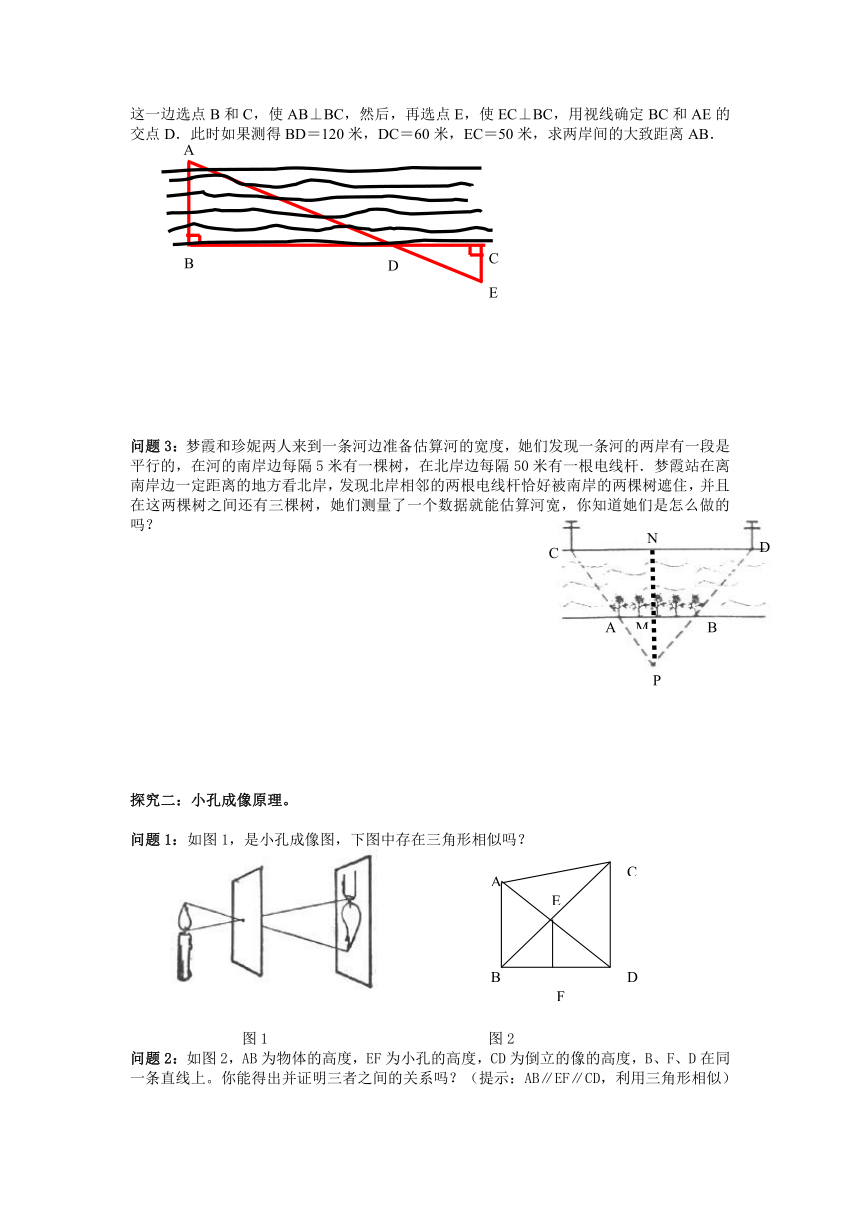
自主预习课本62----63 页 例7,完成下题:
1.如图,要测量河两岸相对的两点A、B的距离,在AB
的垂线BF上取两点C、D,使BC=CD,在作出BF的垂线
DE,使ACE在一条直线上,这时测得DE=16米,则
AB= 米
2.如图,测得BD=60m,DC=30m,EC=25m,求河宽AB。
相似三角形的基本性质是什么?
探究一:测量河宽
问题1:如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
问题2: 如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.
问题3:梦霞和珍妮两人来到一条河边准备估算河的宽度,她们发现一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.梦霞站在离南岸边一定距离的地方看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,她们测量了一个数据就能估算河宽,你知道她们是怎么做的吗?
探究二:小孔成像原理。
问题1:如图1,是小孔成像图,下图中存在三角形相似吗?
图1 图2
问题2:如图2,AB为物体的高度,EF为小孔的高度,CD为倒立的像的高度,B、F、D在同一条直线上。你能得出并证明三者之间的关系吗?(提示:AB∥EF∥CD,利用三角形相似)
问题3:如图,在梯形ABDC中GF是过对角线交点且平行于底的线段,请问:EF与EG的大小关系并说明理由?图中有哪些面积相等的三角形?
1.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高 。
2. 小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,则球拍击球的高度h.(设网球是直线运动)为 。
3.如图,为了测量水塘边A、B两点之间的距离,在可以看到A、B的点
E处,取AE、BE延长线上的C、D两点,使得CD∥AB,若测得CD=5m,
AD=15m,ED=3m,则A、B两点间的距离为 。
4.如图,小东设计两个直角来测量河宽DE,他量得AD=2m,
BD=3m,CE=9m,则河宽DE为 ( )
(A).5m (B).4m (c).6m (D).8m
5.为了测量一池塘的宽AB,在岸边找到了一点C,使AC⊥AB,在AC上找到一点D,在BC上找到一点E,使DE⊥AC,测出AD=35m,DC=35m,DE =30m,那么你能算出池塘的宽AB吗
6.如图,零件的外径为16cm,要求它的壁厚x,需要先求出内径AB,
现用一个交叉钳(AD与BC相等)去量,若测得OA:OD=OB:OC=3:1,
CD=5cm,你能求零件的壁厚x吗?
预 习 检 测
A
B
D
C
E
课 前 准 备
交 流 合 作
P
b
R
Q
a
T
S
A
E
B
D
C
N
M
D
B
A
P
C
A
B
C
F
E
D
A
B
C
F
E
D
G
达 标 检 测
┏
┛
o
B
D
C
A
1m
16m
0.5m
A
D
B
C
E
┏
┏
C
第1题
第2题
A
B
D
C
E
E
B
C
A
D
A
B
C
D
E
课 后 反 思
C
测量物体宽度问题
序 号:( 12 )
年 级: 九年级 单元名称:第24章相似图形的性质
课 型: 新授课 上课时间:
学习内容:华东师大版课本62----63 页 例7
学习目标:1.进一步巩固相似三角形的知识.
2.能够运用三角形相似的知识,解决不能直接测量物体的度宽问题。
重 点:运用三角形相似的知识计算不能直接测量物体的宽度问题.
难 点:如何把实际问题抽象为数学问题
学法指导:合作探究
学 习 过 程
自主预习课本62----63 页 例7,完成下题:
1.如图,要测量河两岸相对的两点A、B的距离,在AB
的垂线BF上取两点C、D,使BC=CD,在作出BF的垂线
DE,使ACE在一条直线上,这时测得DE=16米,则
AB= 米
2.如图,测得BD=60m,DC=30m,EC=25m,求河宽AB。
相似三角形的基本性质是什么?
探究一:测量河宽
问题1:如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
问题2: 如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.
问题3:梦霞和珍妮两人来到一条河边准备估算河的宽度,她们发现一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.梦霞站在离南岸边一定距离的地方看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,她们测量了一个数据就能估算河宽,你知道她们是怎么做的吗?
探究二:小孔成像原理。
问题1:如图1,是小孔成像图,下图中存在三角形相似吗?
图1 图2
问题2:如图2,AB为物体的高度,EF为小孔的高度,CD为倒立的像的高度,B、F、D在同一条直线上。你能得出并证明三者之间的关系吗?(提示:AB∥EF∥CD,利用三角形相似)
问题3:如图,在梯形ABDC中GF是过对角线交点且平行于底的线段,请问:EF与EG的大小关系并说明理由?图中有哪些面积相等的三角形?
1.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高 。
2. 小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,则球拍击球的高度h.(设网球是直线运动)为 。
3.如图,为了测量水塘边A、B两点之间的距离,在可以看到A、B的点
E处,取AE、BE延长线上的C、D两点,使得CD∥AB,若测得CD=5m,
AD=15m,ED=3m,则A、B两点间的距离为 。
4.如图,小东设计两个直角来测量河宽DE,他量得AD=2m,
BD=3m,CE=9m,则河宽DE为 ( )
(A).5m (B).4m (c).6m (D).8m
5.为了测量一池塘的宽AB,在岸边找到了一点C,使AC⊥AB,在AC上找到一点D,在BC上找到一点E,使DE⊥AC,测出AD=35m,DC=35m,DE =30m,那么你能算出池塘的宽AB吗
6.如图,零件的外径为16cm,要求它的壁厚x,需要先求出内径AB,
现用一个交叉钳(AD与BC相等)去量,若测得OA:OD=OB:OC=3:1,
CD=5cm,你能求零件的壁厚x吗?
预 习 检 测
A
B
D
C
E
课 前 准 备
交 流 合 作
P
b
R
Q
a
T
S
A
E
B
D
C
N
M
D
B
A
P
C
A
B
C
F
E
D
A
B
C
F
E
D
G
达 标 检 测
┏
┛
o
B
D
C
A
1m
16m
0.5m
A
D
B
C
E
┏
┏
C
第1题
第2题
A
B
D
C
E
E
B
C
A
D
A
B
C
D
E
课 后 反 思
C
